
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Pawin Iamprasertkun | + 2769 word(s) | 2769 | 2021-09-22 08:21:39 | | | |
| 2 | Nora Tang | + 511 word(s) | 3280 | 2021-10-27 04:37:18 | | |
Video Upload Options
Ion transport is one of the basic principles of the development of various different technologies that can improve the quality of our lives, such as the ever-growing importance of clean and sustainable energy, the reduction of water scarcity and even the improvement of fundamental medical application knowledge. Ion transport can be defined as the movement of charged ions from one position to another in ion electrolyte solutions within both organic (living cells) and inorganic (polymer materials) systems. Ion transport can be encouraged through various mechanisms such as electrochemical diffusion, ion active transport requiring external energy or bulk transport for the conversion of adenosine triphosphate (ATP) and energy consumption in biological functions.
1. Introduction
Ion transport is one of the basic principles of the development of various different technologies that can improve the quality of our lives, such as the ever-growing importance of clean and sustainable energy, the reduction of water scarcity and even the improvement of fundamental medical application knowledge. Ion transport can be defined as the movement of charged ions from one position to another in ion electrolyte solutions within both organic (living cells) and inorganic (polymer materials) systems. Ion transport can be encouraged through various mechanisms such as electrochemical diffusion, ion active transport requiring external energy or bulk transport for the conversion of adenosine triphosphate (ATP) and energy consumption in biological functions [1]. This can be clearly seen in the sodium/potassium (Na + /K + ) ions exchange pump, which is an important ion transportation mechanism that generally occurs in living cell membranes such as plant and animal cells [1][2]. For example, the electric eel possesses a system which demonstrates the evolution of biological membranes under ionic concentration gradients that provide ion transport for power generation. By combining a number of membranes with highly packed selectively ionic channels, electric eels can produce a strong current density which can discharge up to 600 Volts [3]. Ion transportation can be used as a potential way of understanding the mechanism involved in order to explore the mimicking effect of artificial membranes for various ion transport-based applications such as film-based catalysts for gas production (hydrogen and oxygen evolution reactions) [4][5], energy storages (capacitors and batteries) [6][7][8], and membranes for ionic and molecular separation [9][10][11]. Instead of artificial membranes in living cells, ions transport can also relate to cell stabilities, helping us to understand the fundamental mechanisms of ion transport in vitro and in vivo [12].
Two-dimensional (2D) materials are emerging categories of nanostructure materials which include graphene [13][14], transition metal dichalcogenides (TMDs) [11], hexagonal boron nitrile (h-BN) [15], and MXene [16]. The structure of these 2D materials can be controlled in many forms, including being stabilized in single or multiple layers or forming heterostructures, offering unique properties (electrical, thermal, optical and electrochemical, to name just a few) when compared to higher dimensional materials in bulk form [17]. For example, graphene displays higher levels of conductivity (including electrical and thermal conductivity) and a higher surface area than graphite [18]. Meanwhile, TMDs provide better optical properties than graphene materials due to their tuneable band gaps, which can be modified by reducing material thickness and used for optical applications in the visible spectrum. In addition, h-BN is categorized as an insulator that has a smooth surface and only a minimal lattice mismatch with graphite [19][20]. This leads to ultrahigh carrier mobility in graphene when it is integrated with h-BN [21][22][23].
The review describes the fundamental properties of capacitance and ion transport in various 2D materials, and offers novel applications based on various potential technologies from the macro to the nanoscopic perspective. The review describes a well-known capacitance models, including the Helmholtz, Gouy-Chapmann and Stern-Otto models, as well as the capacitive model in two dimensional materials, which explain their ion transport properties. We also show that, in addition to energy storages (i.e., supercapacitors and osmotic energy), the ion-transport devices (i.e., the stimulus-responsive microsupercapacitors) can generate new functionalities through their response to the external stimulus. Such functionalities include direct visualization of energy storages, light-induced energy storage and photodetections, and ion transport controls, as shown in Figure 1 . These prominent, man-made technologies imitate the ion transport in living cells. To understand the extended capabilities of ion transport in artificial devices, it is important to connect with natural phenomena in living bacterial cells. This review aims to provide a better understanding of fundamental knowledge of ion transport technologies in order to examine further potential applications.
2. Principle of Ion Transport
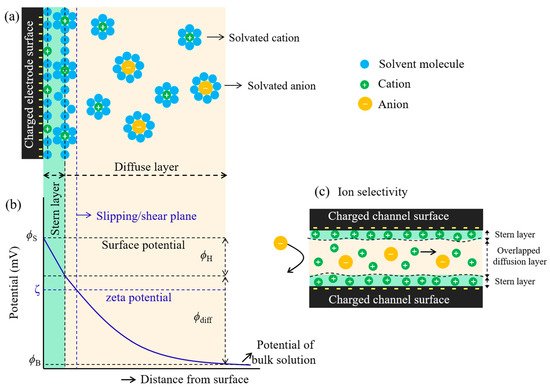
The cations and anions can be separated out due to the charged channel surface. This is because the opposite charged ions (the counter-ions) would preferentially transport through the surface-charged channel faster than the same charged ions (co-ions). This is so-called ion selectivity which is based on the electrical double layer (EDL) structure of the charge distribution at the interface between a charged electrode surface and the surrounding electrolyte solution. The phenomena occurs via electrostatic interaction at which the charged channel surface attracts the counter-ions and repels the co-ions ( Figure 2 a) [1][24] , This results in a decrease in co-ions concentration and an increase in counter-ion concentration. This causes the local potential to decrease as a function of the charged electrode surface-electrolyte distance, as shown in Figure 2 b. The two layers are the stern layer and the diffusion layer. The stern layer, known as the compact (rigid) layer, possesses two planes. The first plane, which is located at the surface, contains solvent molecules and charged ions adsorbed tightly onto the charged surface. The adsorbed ions are defined as specifically adsorbed ions (counter-ions) at which point they are not solvated. Moving further away into the second plane, solvated ions are then encountered due to their increase in solvated ions size which is unable to reach near the surface. The interaction between the solvated ions and the charged surface is governed by coulombic forces as the solvated ions are non-specifically adsorbed [24][25][26]. The diffuse layer lies beyond the stern layer, in which the solvated ions start to be more scattered and increasingly less ordered when stepping away from the charged surface. The ion distribution of this layer is influenced by coulombic interactions between charged ions and charged electrode surface, and thermal motions. This indicates that the potential-distance profile has two regions that are linear (stern layer) and non-linear (diffuse layer), where the potential decay as a function of distance from the charged electrode surface ( Figure 2 b). The density of solvated ions in the diffuse layer is much tighter at high electrode potential and less tight when they are away from the charged surface [24][25][26]. This causes the exponential decrease in potential as a function of diffuse layer distance. Moreover, the thickness of the EDL also relates to the Debye screening length ( λ ), which depends on the ionic strength ( I ) of the electrolyte, corresponding to λ α I −1/2 [27]. For the nanocapillary channel, the thickness of the EDL plays a crucial role in ion transport, at which the EDL of the opposite charged surfaces are overlapped together. This can be attributed to the formation of almost a unipolar ions in the channel (abundant counter-ions), which can be observed in ion selectivity during transport through the channel, as shown in Figure 2 c.
The process of ion transport in nanochannels has received a great deal of attention This plays a crucial role in the development of nanofluidics, ion sieving [9][11][28], and other nanoscale technologies such as energy storage [4][29], active ion gated control [30], and ion rectifications [31]. This has inspired various research directions into the fabrication of synthetic nanochannels from inorganic materials with well-defined properties (various types of geometries) and studying the mechanisms of ion transport [32]. As a development in nanochannel fabrication, this can allow researchers to study electrokinetic models of the transport of electrolyte ions through nanometer-sized slits [33][34][35]. Nanochannels can initially be fabricated from silica (lab-on-a-chip) with a height of 100 nm ( Figure 3 a) [35], and it was found that a steady conductance at low salt concentrations inside the nanochannels results from the dominance of surface charge density in the nanochannels. This leads to the effectiveness of the surface charge density in the nanochannels, leading to the abundance of counter-ions which results in electroneutrality inside the channels [34][35]. Schoch et al. [34] increased the surface-area-to-volume-ratio by reducing the height of channel to 50 nm ( Figure 3 b), showing that the surface charge plays a crucial role as a greater fraction of the total charge is attached to the channel’s wall. This is attributed to the regulation of ionic flow inside the charged nanochannels.
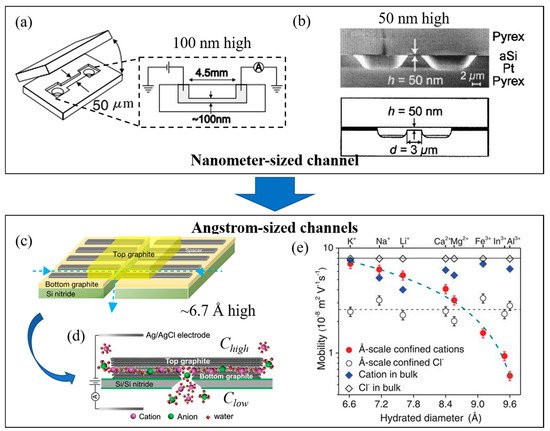
To control ionic current during the transport of ions through a channel, the height of the channel should be less than the Debye screen length (1–100 nm in height) and the channel’s wall should be charged [38]. A unipolar solution of counter-ions can be created inside the nanochannel at the electrolyte concentration neutralizing the surface charge, while the co-ions are electrostatically repelled from the channel’s wall. This creates the ionic current inside the channel which depends on the surface charge density in the concentration – although the ionic current becomes less involved in surface charge density where the bulk concentration increases [31][38]. The height of the channel should be similar to the nanoscale channels inside transmembrane proteins, which control the transport of ions and molecules. As the magnitude of the EDL is evaluated from the Debye screening length, which relates to the ionic concentration, this causes the overlapping EDL inside the channel depending on the relation between size of channels and the ion concentration. Due to traditional synthetic channels with heights in the range of 1–100 nm, the EDL overlap can occur at very low concentrations (<10 mM), which is far lower than the concentrations observed in physiological solutions [30]. Duan et al. [30] demonstrated ion transport by reducing the size of nanochannel to 2 nm in height, providing the connecting EDLs from each side of channel’s wall at 100 mM concentration, which is close to physiological concentrations. The fluid nanochannels thus obtained can be used to mimic protein channels in order to study the ion/molecular transport in liquid nanoconfinement [30][31][32].
Although an SiO2/Si-based nanochannel with a 2 nm height with hydrophilic surfaces showed almost four-fold increase in ion transport when compared to a 25 nm height channel in terms of bulk ion transport, but the mechanism behind the process is not fully understood [30]. The process may result from the overlapping of the hydrogen bonding network of the two hydration shells next to the hydrophilic surfaces [30]. To understand and prove this, the hydrophobic nanochannels should be fabricated under the same experiment conditions. Jung et al. [39] first fabricated rectangular-shaped nanochannels using graphene nanosheets across the surface to provide the hydrophobic noanoconfinement [39][40]. They found that the 3.6 nm graphene-based nanochannels performed an excellent level of ion transport, providing great ionic conductance by over two orders of magnitude compared to the nanochannels in the absence of graphene coating in an aqueous solution. This can be explained by the fact that the surface of the graphene nanochannels is much cleaner and smoother than that the SiO 2/Si nanochannels (10–50 nm height channels showing significantly low ion transport).
3. Ionic Sieving through 2D Material-Based Membranes
A membrane can be defined as a thin physical interfacial material which possesses specific chemical and/or physical properties to control a selective species (i.e., charged ions/molecules, live cells, and various size of particles) passing through. In general, it can be classified by cross-sectional properties into isotropic membranes (homogeneous composition; microporous, nonporous dense, and electrically charged membranes) and anisotropic membrane (heterogeneous composition; Loeb-Sourirajan and thin-film composite membranes) [41][42]. As the various structures and function inside membranes, this can be used to control the transport of permeants which is based on pore size of membranes, diffusion (driven by concentration or pressure), and electrostatic repulsion. The different types of membranes are widely implemented for various filtration technologies such as particle separations (large molecules, gas, and ions), pervaporation, and reverse osmosis (RO) membranes. Electrically charged membranes can be classified as positively or negatively charge functional groups in the structural materials, which is so-called an anion-exchange membrane (AEM) and a cation-exchange membrane (CEM), respectively [41]. The mechanism of separation is mainly based on the electrostatic repulsion of the similar charge between the charge inside the membrane and charge of particles under the influence of an applied electric potential. The ion-exchange membranes (IEM) can be produced from various materials such as organic (e.g., liquid and polymer) [43][44], inorganic (e.g., carbon nanotube, graphene, transition metal dichalcogenides) [9][11][45], and organic-inorganic hybrid (e.g., metal organic framework) materials [46][47][48].
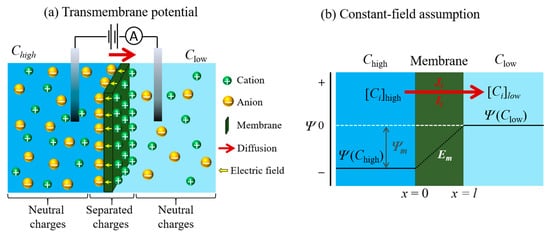
Membrane potential is defined as the electrical potential arising from the difference in ionic concentrations on each side of a semipermeable membrane. It is also known as transmembrane potential, and the phenomenon has been widely studied in biological cell membranes such as neurons and muscle cells. The application of an electric field across the membrane allows us to determine the charge and size selective ion sieving through the nanoporous graphene (NPG) membranes [49], angstrom-scale slits [37] and laminar stacked 2D membranes [9][10][11][50]. The principle of membrane potential will be discussed in this section in the context of the model used.
The Nernst equation is used to determine the equilibrium state of the membrane when the membrane is permeable to only a single type of ion. However, if several types of ions on both sides are involved in the flow through the membrane (i.e., the membrane is permeable to various ions) then membrane potential can be evaluated using the Goldman-Hodgkin-Katz (GHK) equation, which allows the selective determination of ion. This equation is an extended version of the Nernst equation.
Based on the assumption of the GHK equation [51][52], the electrodiffusion model is used to assume the flow of an ion through the membrane, which is associated with various conditions. The conditions considered are based on a homogeneous slab of material (one that is uniform, planar and infinite in its lateral extent), a constant electric field (the potential decreases linearly within the membrane), a material in which ions can move across the membrane independently (without interacting with one another), and have constant permeability, P , (where P = βD / l ; β , D , and l are the partition coefficient, the diffusion coefficient, and the membrane thickness, respectively) [1][52][53][54]. In this assumption, the x -axis is used to represent the direction of the flow of ions through the membrane. Thus, the origin of the flow lies at the interface of the membrane on the feed side (denoted x = 0) and its termination is the interface of the membrane at the permeate side (denoted x = l ) when the membrane thickness is l , as shown in Figure 4 b. As the membrane is assumed to have lateral uniformity, variations in the electric field ( Em ) and ionic concentration ( Ci ) within the membrane are related only to the x -direction. The assumption under the GHK model is that the field inside the membrane is constant and equal to: (12) dE/dx = Ep − Ef l = − E m l where E m is the transmembrane voltage, E p and E f are the potential at the permeate and feed sides of the membrane surface, respectively.
4. Optical Induction with Ion Transport and Optical Techniques for Ion Transport
The utilization of optical techniques for ion transport have recently become available through optical induction [55] and optical investigation [12], but fundamental mechanisms are more ambiguous. It is important to investigate these methods and the extension of boundaries further in biological simulation and manmade applications.
To enhance the effects of ion transport, the structural designs of 2D materials can be used to reengineer the ways in which ions propagate, with a significant jump in the super-diffusive regime [56][57]. When restricted by a 2D planar surface, the diffusion in normal and anomalous diffusion (the sub-diffusive and super-diffusive processes) is a quintessential property. Since our understanding of ion diffusion is a foundation of ion transport, few articles have studied the subject via simulation [56] or experiments [58].
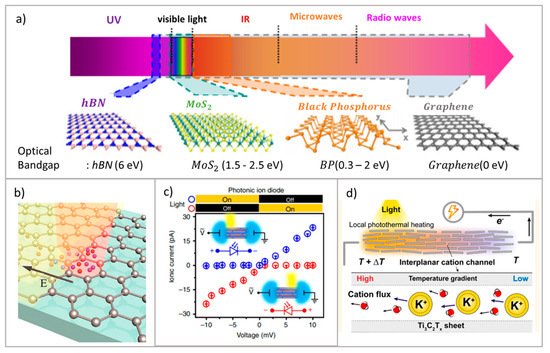
Although photoelectric stimuli occur for ion transport induction, responses from photothermal effects have also been investigated [59]. In stacking MXene nanochannels, the reduction of temperature of Gibbs free energy on light irradiated regions causes non-isothermal ion transport, shown in Figure 5 d, with a response of up to 1 mV per degree Kelvin. This also sheds light on photothermal ionic transport applications, which have the potential for 1.68 mWm −2 output [59].
Fluorescent markers can be utilized for ion transport in neuron cells, and can also be used to indicate molecular interactions and transport through bacterial membrane [63][64][65]. With more complicates pathways because of their molecular specificity, the transport of ions or charged molecules relates to mechanisms of ion transport through nanopore (1D diffusion) and on membrane surfaces (2D diffusion) [66]. The transport of charged molecules in respect of ion transport utilizes fluorescent techniques for fundamental investigation [67]. Charged molecules of antimicrobial peptide (AMPs) were reported to have been transported through the bacterial membrane [63].
References
- Hille, B. Ion Channels of Excitable Membranes, 3rd ed.; Sinauer: Sunderland, MA, USA, 2001; Chapter 14.
- Xiao, K.; Jiang, L.; Antonietti, M. Ion Transport in Nanofluidic Devices for Energy Harvesting. Joule 2019, 3, 2364–2380.
- Gotter, A.L.; Kaetzel, M.A.; Dedman, J.R. Electrophorus electricus as a Model System for the Study of Membrane Excitability. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 1998, 119, 225–241.
- Hirunpinyopas, W.; Rodgers, A.N.J.; Worrall, S.D.; Bissett, M.A.; Dryfe, R.A.W. Hydrogen Evolution at Liquid|Liquid Interfaces Catalyzed by 2D Materials. Chem. Nano Mat. 2017, 3, 428–435.
- Kahan, R.J.; Hirunpinyopas, W.; Cid, J.; Ingleson, M.J.; Dryfe, R.A.W. Well-Defined Boron/Nitrogen-Doped Polycyclic Aromatic Hydrocarbons are Active Electrocatalysts for the Oxygen Reduction Reaction. Chem. Mater. 2019, 31, 1891–1898.
- Iamprasertkun, P.; Hirunpinyopas, W.; Deerattrakul, V.; Sawangphruk, M.; Nualchimplee, C. Controlling the Flake Size of Bifunctional 2D WSe2 Nanosheets as Flexible Binders and Supercapacitor Materials. Nanoscale Adv. 2021, 3, 653–660.
- Worrall, S.D.; Bissett, M.A.; Hirunpinyopas, W.; Attfield, M.P.; Dryfe, R.A.W. Facile Fabrication of Metal–Organic Framework HKUST-1-Based Rewritable Data Storage Devices. J. Mater. Chem. C 2016, 4, 8687–8695.
- Tibodee, A.; Hirunpinyopas, W.; Jeamjumnunja, K.; Sirisaksoontorn, W. Synthesis of Carbon Dots from the Biomass Products for Supercapacitor Applications. IOP Conf. Ser. Mater. Sci. Eng. 2020, 773, 012022.
- Hirunpinyopas, W.; Iamprasertkun, P.; Bissett, M.A.; Dryfe, R.A.W. Tunable Charge/Size Selective Ion Sieving with Ultrahigh Water Permeance through Laminar Graphene Membranes. Carbon 2020, 156, 119–129.
- Hirunpinyopas, W.; Prestat, E.; Iamprasertkun, P.; Bissett, M.A.; Dryfe, R.A.W. Potential Dependent Ionic Sieving through Functionalized Laminar MoS2 Membranes. 2D Mater. 2020, 7, 015030.
- Hirunpinyopas, W.; Prestat, E.; Worrall, S.D.; Haigh, S.J.; Dryfe, R.A.W.; Bissett, M.A. Desalination and Nanofiltration Through Functionalized Laminar MoS2 Membranes. ACS Nano 2017, 11, 11082–11090.
- Senthil Murugan, A.; Kiruthika, M.; Abel Noelson, E.R.; Yogapandi, P.; Gnana kumar, G.; Annaraj, J. Fluorescent Sensor for in-Vivo Bio-Imaging, Precise Tracking of Fe3+ ions in Zebrafish Embryos and Visual Measuring of Cu2+ Ions in Pico-Molar Level. Arabian J. Chem. 2021, 14, 102910.
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669.
- Novoselov, K.S.; Jiang, D.; Schedin, F.; Booth, T.J.; Khotkevich, V.V.; Morozov, S.V.; Geim, A.K. Two-Dimensional Atomic Crystals. Proc. Natl. Acad. Sci. USA 2005, 102, 10451–10453.
- Cassabois, G.; Valvin, P.; Gil, B. Hexagonal Boron Nitride Is An Indirect Bandgap Semiconductor. Nat. Photonics 2016, 10, 262.
- Naguib, M.; Mochalin, V.N.; Barsoum, M.W.; Gogotsi, Y. 25th Anniversary Article: MXenes: A New Family of Two-Dimensional Materials. Adv. Mater. 2014, 26, 992–1005.
- Iamprasertkun, P.; Hirunpinyopas, W.; Tripathi, A.M.; Bissett, M.A.; Dryfe, R.A.W. Electrochemical Intercalation of MoO3-MoS2 Composite Electrodes: Charge Storage Mechanism of Non-Hydrated Cations. Electrochim. Acta 2019, 307, 176–187.
- Deerattrakul, V.; Hirunpinyopas, W.; Pisitpipathsin, N.; Saisopa, T.; Sawangphruk, M.; Nualchimplee, C.; Iamprasertkun, P. The Electrochemistry of Size Dependent Graphene via Liquid Phase Exfoliation: Capacitance and Ionic Transport. Phys. Chem. Chem. Phys. 2021, 23, 11616–11623.
- Dean, C.R.; Young, A.F.; Meric, I.; Lee, C.; Wang, L.; Sorgenfrei, S.; Watanabe, K.; Taniguchi, T.; Kim, P.; Shepard, K.L.; et al. Boron Nitride Substrates for High-Quality Graphene Electronics. Nat. Nanotechnol. 2010, 5, 722–726.
- Giovannetti, G.; Khomyakov, P.A.; Brocks, G.; Kelly, P.J.; van den Brink, J. Substrate-Induced Band Gap in Graphene on Hexagonal Boron Nitride: Ab Initio Density Functional Calculations. Phys. Rev. B 2007, 76, 073103.
- Mayorov, A.S.; Gorbachev, R.V.; Morozov, S.V.; Britnell, L.; Jalil, R.; Ponomarenko, L.A.; Blake, P.; Novoselov, K.S.; Watanabe, K.; Taniguchi, T.; et al. Micrometer-Scale Ballistic Transport in Encapsulated Graphene at Room Temperature. Nano Lett. 2011, 11, 2396–2399.
- Wang, L.; Meric, I.; Huang, P.Y.; Gao, Q.; Gao, Y.; Tran, H.; Taniguchi, T.; Watanabe, K.; Campos, L.M.; Muller, D.A.; et al. One-Dimensional Electrical Contact to a Two-Dimensional Material. Science 2013, 342, 614.
- Banszerus, L.; Schmitz, M.; Engels, S.; Dauber, J.; Oellers, M.; Haupt, F.; Watanabe, K.; Taniguchi, T.; Beschoten, B.; Stampfer, C. Ultrahigh-Mobility Graphene Devices from Chemical Vapor Deposition on Reusable Copper. Sci. Adv. 2015, 1, e1500222.
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods Fundamentals and Applications, 2nd ed.; Wiley: Hoboken, NJ, USA, 2001.
- Wang, J. Analytical Electrochemistry, 2nd ed.; Wiley: Weinheim, Germany, 2000.
- Pletcher, D. A First Course in Electrode Processes, 2nd ed.; RSC Publishing: London, UK, 2009.
- Sparreboom, W.; van den Berg, A.; Eijkel, J.C.T. Principles and Applications of Nanofluidic Transport. Nat. Nanotechnol. 2009, 4, 713–720.
- Abraham, J.; Vasu, K.S.; Williams, C.D.; Gopinadhan, K.; Su, Y.; Cherian, C.T.; Dix, J.; Prestat, E.; Haigh, S.J.; Grigorieva, I.V.; et al. Tunable Sieving of Ions Using Graphene Oxide Membranes. Nat. Nanotechnol. 2017, 12, 546–550.
- Iamprasertkun, P.; Hirunpinyopas, W.; Keerthi, A.; Wang, B.; Radha, B.; Bissett, M.A.; Dryfe, R.A.W. Capacitance of Basal Plane and Edge-Oriented Highly Ordered Pyrolytic Graphite: Specific Ion Effects. J. Phys. Chem. Lett. 2019, 10, 617–623.
- Duan, C.; Majumdar, A. Anomalous Ion Transport in 2-nm Hydrophilic Nanochannels. Nat. Nanotechnol. 2010, 5, 848–852.
- Karnik, R.; Duan, C.; Castelino, K.; Daiguji, H.; Majumdar, A. Rectification of Ionic Current in a Nanofluidic Diode. Nano Lett. 2007, 7, 547–551.
- Duan, C.; Wang, W.; Xie, Q. Review Article: Fabrication of Nanofluidic Devices. Biomicrofluidics 2013, 7, 026501.
- Schoch, R.B.; Lintel, H.V.; Renaud, P. Effect of the Surface Charge on Ion Transport Through Nanoslits. Phys. Fluids 2005, 17, 100604.
- Schoch, R.B.; Renaud, P. Ion Transport Through Nanoslits Dominated by the Effective Surface Charge. Appl. Phys. Lett. 2005, 86, 253111.
- Stein, D.; Kruithof, M.; Dekker, C. Surface-Charge-Governed Ion Transport in Nanofluidic Channels. Phys. Rev. Lett. 2004, 93, 035901.
- Radha, B.; Esfandiar, A.; Wang, F.C.; Rooney, A.P.; Gopinadhan, K.; Keerthi, A.; Mishchenko, A.; Janardanan, A.; Blake, P.; Fumagalli, L.; et al. Molecular Transport Through Capillaries Made with Atomic-Scale Precision. Nature 2016, 538, 222–225.
- Esfandiar, A.; Radha, B.; Wang, F.C.; Yang, Q.; Hu, S.; Garaj, S.; Nair, R.R.; Geim, A.K.; Gopinadhan, K. Size Effect in Ion Transport Through Angstrom-Scale Slits. Science 2017, 358, 511–513.
- Daiguji, H.; Yang, P.; Majumdar, A. Ion Transport in Nanofluidic Channels. Nano Lett. 2004, 4, 137–142.
- Jung, W.; Kim, J.; Kim, S.; Park, H.G.; Jung, Y.; Han, C.-S. A Novel Fabrication of 3.6 nm High Graphene Nanochannels for Ultrafast Ion Transport. Adv. Mater. 2017, 29, 1605854.
- Algara-Siller, G.; Lehtinen, O.; Wang, F.C.; Nair, R.R.; Kaiser, U.; Wu, H.A.; Geim, A.K.; Grigorieva, I.V. Square Ice in Graphene Nanocapillaries. Nature 2015, 519, 443–445.
- Baker, R.A. Membrane Technology and Applications, 3rd ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2004; p. 575.
- Lee, A.; Elam, J.W.; Darling, S.B. Membrane Materials for Water Purification: Design, Development, and Application. Environ. Sci. Water Res. Technol. 2016, 2, 17–42.
- Ochoa, N.A.; Masuelli, M.; Marchese, J. Development of Charged Ion Exchange Resin-Polymer Ultrafiltration Membranes to Reduce Organic Fouling. J. Membr. Sci. 2006, 278, 457–463.
- Tang, Y.; Xue, Z.; Zhou, X.; Xie, X.; Tang, C.-Y. Novel Sulfonated Polysulfone Ion Exchange Membranes for Ionic Polymer–Metal Composite Actuators. Sens. Actuators B 2014, 202, 1164–1174.
- Kim, A.R.; Vinothkannan, M.; Song, M.H.; Lee, J.-Y.; Lee, H.-K.; Yoo, D.J. Amine Functionalized Carbon Nanotube (ACNT) Filled in Sulfonated Poly(Ether Ether Ketone) Membrane: Effects of ACNT in Improving Polymer Electrolyte Fuel Cell Performance Under Reduced Relative Humidity. Compos. Part B 2020, 188, 107890.
- Vilela, S.M.F.; Navarro, J.A.R.; Barbosa, P.; Mendes, R.F.; Pérez-Sánchez, G.; Nowell, H.; Ananias, D.; Figueiredo, F.; Gomes, J.R.B.; Tomé, J.P.C.; et al. Multifunctionality in an Ion-Exchanged Porous Metal–Organic Framework. J. Am. Chem. Soc. 2021, 143, 1365–1376.
- Kumar, P.; Pournara, A.; Kim, K.-H.; Bansal, V.; Rapti, S.; Manos, M.J. Metal-Organic Frameworks: Challenges and Opportunities for Ion-Exchange/Sorption Applications. Prog. Mater. Sci. 2017, 86, 25–74.
- Kim, A.R.; Vinothkannan, M.; Yoo, D.J. Artificially Designed, Low Humidifying Organic–Inorganic (SFBC-50/FSiO2) Composite Membrane for Electrolyte Applications of Fuel Cells. Compos. Part B 2017, 130, 103–118.
- Rollings, R.C.; Kuan, A.T.; Golovchenko, J.A. Ion Selectivity of Graphene Nanopores. Nat. Commun. 2016, 7, 11408.
- Hong, S.; Constans, C.; Surmani Martins, M.V.; Seow, Y.C.; Guevara Carrió, J.A.; Garaj, S. Scalable Graphene-Based Membranes for Ionic Sieving with Ultrahigh Charge Selectivity. Nano Lett. 2017, 17, 728–732.
- Goldman, D.E. Potential, Impedance, and Rectification in Membranes. J. Gen. Physiol. 1943, 27, 37–60.
- Hodgkin, A.L.; Katz, B. The Effect of Sodium Ions on the Electrical Activity of the Giant Axon of the Squid. J. Physiol. 1949, 108, 37–77.
- Sandblom, J.P.; Eisenman, G. Membrane Potentials at Zero Current: The Significance of a Constant Ionic Permeability Ratio. Biophys. J. 1967, 7, 217–242.
- MacGillivray, A.D.; Hare, D. Applicability of Goldman’s Constant Field Assumption to Biological Systems. J. Theor. Biol. 1969, 25, 113–126.
- Yang, J.; Liu, P.; Li, L.; Tang, Z. Light-Driven Active Ion Transport. Chem. Eur. J. 2020, 26, 13748–13753.
- Gervilla, V.; Zarshenas, M.; Sangiovanni, D.G.; Sarakinos, K. Anomalous versus Normal Room-Temperature Diffusion of Metal Adatoms on Graphene. J. Phys. Chem. Lett. 2020, 11, 8930–8936.
- Massaro, A.; Pecoraro, A.; Muñoz-García, A.B.; Pavone, M. First-Principles Study of Na Intercalation and Diffusion Mechanisms at 2D MoS2/Graphene Interfaces. J. Phys. Chem. C 2021, 125, 2276–2286.
- Kühne, M.; Zhao, D.; Zschieschang, U.; Buck, R.; Müller, M.; Klauk, H.; Smet, J.H. Wettability Engineering for Studying Ion Transport in 2D Layered Materials. Adv. Mater. Interfaces 2021, 8, 2001453.
- Hong, S.; Zou, G.; Kim, H.; Huang, D.; Wang, P.; Alshareef, H.N. Photothermoelectric Response of Ti3C2Tx MXene Confined Ion Channels. ACS Nano 2020, 14, 9042–9049.
- Xia, F.; Wang, H.; Xiao, D.; Dubey, M.; Ramasubramaniam, A. Two-Dimensional Material Nanophotonics. Nat. Photonics 2014, 8, 899–907.
- Liu, C.-H.; Chang, Y.-C.; Lee, S.; Zhang, Y.; Zhang, Y.; Norris, T.B.; Zhong, Z. Ultrafast Lateral Photo-Dember Effect in Graphene Induced by Nonequilibrium Hot Carrier Dynamics. Nano Lett. 2015, 15, 4234–4239.
- Yang, J.; Hu, X.; Kong, X.; Jia, P.; Ji, D.; Quan, D.; Wang, L.; Wen, Q.; Lu, D.; Wu, J.; et al. Photo-Induced Ultrafast Active Ion Transport Through Graphene Oxide Membranes. Nat. Commun. 2019, 10, 1171.
- Gong, H.; Liao, M.; Hu, X.; Fa, K.; Phanphak, S.; Ciumac, D.; Hollowell, P.; Shen, K.; Clifton, L.A.; Campana, M.; et al. Aggregated Amphiphilic Antimicrobial Peptides Embedded in Bacterial Membranes. ACS Appl. Mater. Interfaces 2020, 12, 44420–44432.
- Park, S.-H.; Kwon, N.; Lee, J.-H.; Yoon, J.; Shin, I. Synthetic Ratiometric Fluorescent Probes for Detection of Ions. Chem. Soc. Rev. 2020, 49, 143–179.
- Shashkova, S.; Leake, M.C. Single-Molecule Fluorescence Microscopy Review: Shedding New Light on Old Problems. Biosci. Rep. 2017, 37.
- Sözer, E.B.; Pocetti, C.F.; Vernier, P.T. Transport of Charged Small Molecules after Electropermeabilization—Drift and Diffusion. BMC Biophys. 2018, 11, 4.
- Kapanidis, A.N.; Uphoff, S.; Stracy, M. Understanding Protein Mobility in Bacteria by Tracking Single Molecules. J. Mol. Biol. 2018, 430, 4443–4455.




