
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Raman R. K. Singh | + 1706 word(s) | 1706 | 2021-10-09 06:12:18 | | | |
| 2 | Bruce Ren | Meta information modification | 1706 | 2021-10-25 03:21:57 | | | | |
| 3 | Bruce Ren | Meta information modification | 1706 | 2021-10-29 08:49:38 | | | | |
| 4 | Lindsay Dong | Meta information modification | 1706 | 2021-11-12 09:20:01 | | |
Video Upload Options
Stress corrosion cracking (SCC) is a vexing problem for load-bearing equipment operating in a corrosive environment in various industries, such as aerospace, chemical and mineral processing, civil structures, bioimplants, energy generation etc. For safe operation, effective maintenance and life prediction of such equipment, reliable design data on SCC (such as threshold stress intensity for SCC, i.e., KISCC) are invaluable. Generating reliable KISCC data invariably requires a large number of tests. Traditional techniques can be prohibitively expensive. Circumfrential notch tensile testing is a relatively recent, much simpler and cost-effective approach to generating accurate and reliable KISCC data.
1. Introduction
- (a)
-
It can occur at stresses even below the yield strength of the material;
- (b)
-
Cracks can grow undetected into leaks or, sometimes, sudden and catastrophic failures when the required synergy of stress and environment is present;
- (c)
-
A few localized and fine cracks may grow undetected to fracture, while the alloy surface may virtually appear free from corrosion;
- (d)
-
It is intriguing that sometimes a relatively less corrosive environment may be more deleterious for SCC.
2. Circumferential Notch Tensile (CNT) Testing for KISCC: Distinct Advantages
- (a)
-
It enables achieving high stress intensities (KI) by employing small loads;
- (b)
-
It is much easier to machine the simple cylindrical specimen geometry than the CT or DCB geometry;
- (c)
-
It is much cheaper to fabricate the specimens (cf. 20–25% of CT or DCB specimens);
- (d)
-
Enables testing when only thin sections are available (such as HAZ of weldments or a failed thin-walled component);
- (e)
-
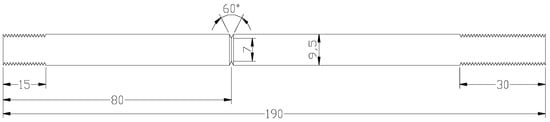
It vastly reduces the amount of the required test material. In fact, the required test material can be further reduced considerably by using extenders. The extenders constructed out of another material can be used because the actual area of interest is only the notched portion and the adjacent area (shown in Figure 1). This enables just machining the small cylindrical sample with circumferential notch and then extending it to the full length by drilling threads on both ends (and then using extenders of a harder material to extend the length at each end);
- (f)
-
The ability to test small cylindrical samples (as described at (e) above) enables testing where only small lengths of test material may be available or where the test material is expensive (for example, when a large number of tests are required for assessing a pressure vessel constructed out of an expensive duplex stainless steel).
2.1. CNT Specimens for the Determination of KISCC: Challenges and Circumvention
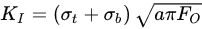
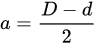
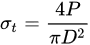
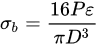
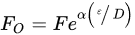
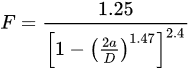
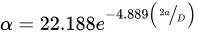
2.2. Accounting for Eccentricity (ε) in Pre-Cracked CNT Specimens
In a nutshell, the effective crack length (a) in Equation (1) is used for the first estimate of KI, which enables the determination of the Irwin correction factor (ry) from Equation (8), and (a¯) from Equation (9). Thus, Equation (1) enables the determination of KI.
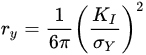
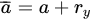
where σy is 0.2% offset tensile yield stress (Pa). Using a in Equation (2), the first estimate of KI is determined. a¯ (instead of a) is used for the calculation of KI. The reason for this correction is described elsewhere [11,12,13,14].

Figure 2. Eccentricity of fatigue crack in a CNT specimen that was subjected to rotating–bending fatigue [1].
2.3. Valid KI Data
The implementation of elastic fracture mechanics (LEFM) for the determination of KI assumes primarily an elastic deformation and brittle state of the material. In reality, there is invariably some contribution of plastic deformation at the crack tip before a crack propagates. Therefore, the LEFM approach allows for a small plastic zone, as long as its contribution is negligibly insignificant, which necessitates the specimen size to be large. For its implementation, two specifications have been developed for determining the validity of the measured KI, as described below [8,9,10]:
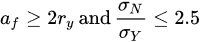
whereaf=ε+(D−2am−d)2, and σN is the nominal applied stress in the final ligament (Pa).
In other words, the validity requirements insist that: (i) the correction in depth due to the Irwin plastic zone (ry) should be at least half of the fatigue pre-crack depth (af) [10][11][12] and (ii) the average of the stress across the ligament produced upon fatigue pre-cracking (σN) should be smaller than 2.5 times the yield strength (σy). In the context of pre-cracked CNT specimens that may have eccentric final ligament, these validity specifications can also apply (where the maximum nominal stress has contributions from both the tensile and the bending stresses which should be <2.5 σy). Also, for such eccentric ligaments, the greatest depth of the crack is taken to be the fatigue crack depth (af).
References
- Raman, R.K.S.; Rihan, R.; Ibrahim, R.N. A novel approach to the determination of the threshold for stress corrosion cracking (K ISCC) using round tensile specimens. Metall. Mater. Trans A 2006, 37A, 2963–2973.
- Sedriks, A.J. Stress Corrosion Cracking Test Methods; Publications of National Association of Corrosion Engineers: Houston, TX, USA, 1990.
- Dean, S.W.; Pugh, E.N.; Ugiansky, G.M. Environment-Sensitive Fracture: Evaluation, and Comparison of Test Methods, ASTM STP 821, Symposium Sponsored by ASTM Committee G-1; ASTM: Philadelphia, PA, USA, 1982.
- Turnbull, A. Test methods for environment assisted cracking. Br. Corros. J. 1992, 27, 271–289.
- Raman, R.K.S.; Rihan, R.; Ibrahim, R.N. Role of imposed potentials in threshold for caustic cracking susceptibility (KISCC): Investigations using circumferential notch tensile (CNT) testing. Corros. Sci. 2007, 49, 4386–4439.
- Rihan, R.; Raman, R.K.S.; Ibrahim, R.N. Determination of crack growth rate and threshold for caustic cracking (KIscc) of a cast iron using small circumferential notched tensile (CNT) specimens. Mater. Sci. Eng. A 2006, 425, 272–277.
- Raman, R.K.S.; Rihan, R.; Ibrahim, R.N. Validation of a novel approach to determination of threshold for stress corrosion cracking (KISCC). Mate. Sci. Eng. A 2007, 452–453, 652–656.
- Ibrahim, R.N.; Stark, H.L. Establishing K 1c from eccentrically fatigue cracked small circumferentially grooved cylindrical specimens. Int. J. Fracture 1990, 44, 179–188.
- Ibrahim, R.N.; Kotousov, A.G. Analytical approach for calculating KIC from eccentrically cracked cylindrical specimens. ASME Press. Vessel. Pip. Conf. 1999, 388, 155–161.
- Ibrahim, R.N.; Stark, H.L. Estimating fracture toughness from small specimens. Eng. Fract. Mech. 1986, 25, 395–401.
- Ibrahim, R.N. Eccentricity Correction for the Evaluation of Fracture Toughness from Cylindrical Notched Test Small Specimens. Eng. Fract. Mech. 1999, 64, 49–58.
- Ibrahim, R.N.; Stark, H.L. Validity requirements for fracture toughness measurements obtained from small circumferentially notched cylindrical specimens. Eng. Fract. Mech. 1987, 28, 455–460.





