Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Subramanian Boopathi
 + 3323 word(s) 3323 2021-10-13 10:24:47 |
2 update layout and reference
Rita Xu
 Meta information modification 3323 2021-10-22 04:52:46 |

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Boopathi, S.; Poma, A.B. Amyloid Beta Oligomers. Encyclopedia. Available online: https://encyclopedia.pub/entry/15250 (accessed on 16 November 2024).
Boopathi S, Poma AB. Amyloid Beta Oligomers. Encyclopedia. Available at: https://encyclopedia.pub/entry/15250. Accessed November 16, 2024.
Boopathi, Subramanian, Adolfo B. Poma. "Amyloid Beta Oligomers" Encyclopedia, https://encyclopedia.pub/entry/15250 (accessed November 16, 2024).
Boopathi, S., & Poma, A.B. (2021, October 21). Amyloid Beta Oligomers. In Encyclopedia. https://encyclopedia.pub/entry/15250
Boopathi, Subramanian and Adolfo B. Poma. "Amyloid Beta Oligomers." Encyclopedia. Web. 21 October, 2021.
Amyloid Beta Oligomers
Edit
This entry is adapted from the peer-reviewed paper 10.3390/ijms221910798

Amyloid beta (Aβ) oligomers are the most neurotoxic aggregates causing neuronal death and cognitive damage. A detailed elucidation of the aggregation pathways from oligomers to fibril formation is crucial to develop therapeutic strategies for Alzheimer’s disease (AD). This review mainly focused on future perspective of Aβ peptide research using computer simulations.

Alzheimer’s disease amyloid β peptide plaque formation

1. Introduction

Approximately 50 million people are globally affected by Alzheimer’s Disease (AD) [1][2]. This number will increase to 150 million by 2050 unless new prevention treatments become available [1]. Amyloid plaques and neurofibrillary tangles in brain tissue are the main hallmarks of AD. Amyloid plaques are composed of amyloid β (Aβ) peptides. Neurofibrillary tangles are composed of hyperphosphorylated tau proteins. In 1992, Hardy and Higgins [2] developed the amyloid cascade hypothesis; Aβ aggregates are transformed into Aβ fibrils that accumulate in the brain and finally trigger neurodegeneration.
Amyloid precursor protein (APP) gene generates three variant APP695, APP751 and APP770, which are produced in neurons, endothelial cells, and platelets, respectively. In the aggregation pathway, transmembrane APP695 is cleaved by β- and γ-secretase to generates Aβ1-40 and Aβ1-42 peptides. During the APP695 cleavage, two processes occur (Figure 1). (1) Aβ is released to the extracellular hydrophobic environment, where Aβ monomers assemble into dimers, trimers, tetramers, oligomers, and fibrils [3][4][5][6], Aβ fibrils constitute the amyloid plaques considered a major pathological hallmark of AD. (2) A small amount of Aβ remains above the cellular membrane and can form membrane-associated Aβ oligomers that disrupt the shape of the membrane [7]. The amyloid fibrils are generally insoluble and transform into plaques. The Aβ oligomers are soluble and mainly spread throughout AD affected brain. Soluble Aβ oligomers deposited approximately 3–4 kDa in the AD brain could affect the calcium ion channel activity in synapsis through disrupting nerve signal transmission and damage mitochondrial causes to increase free radial lead to cell death. Soluble oligomers reach 10–100 kDa, which is considered more cytotoxicity than amyloid fibril aggregation; thus, the soluble oligomers exposed higher toxicity when compared with an insoluble fibril structure [8]. The water-mediated attraction in Aβ peptides and high propensity favor the formation of insoluble amyloid fibrils. The oligomers and fibrils conformation are recognized as a generic antibody epitope [9]. Although the relationship between oligomers and fibrils is still under debate, soluble and insoluble Aβ structures have been targeted to develop a cure for AD.
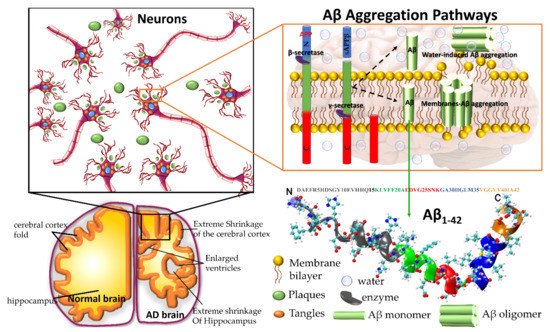
Ijms 22 10798 g001 550
Figure 1. Plaques are around the neurons and tangles inside the neurons. Plaques and tangles are involved in killing the neurons resulting in drastic shrinking of the brain compared to normal brain. β-secretase cleaves APP (composed of 695 amino acids) into the membrane-tethered C-terminal fragments β (CTFβ or C99) and N-terminal sAPPβ. Aβ is obtained after the sequential cleavage of CTFβ by γ-secretases. Upon APP cleavage, two mechanism pathways have been proposed, in the first, Aβ is released to the extracellular environment, due to its hydrophobic nature, formed Aβ aggregates, in the second, a small amount of Aβ remains in the membrane evolving into membrane-associated Aβ aggregates. Aβ peptide has divided into five regions, N-terminus or hydrophilic region represent in grey, Central hydrophobic region in green, Loop region in red, second hydrophobic region in blue and C-terminal in orange. AD brain shrunken as compared with Healthy one.
Molecular insight into aggregation pathways from oligomers to fibril formation remains an open problem in amyloidogenesis. A recent study reported [10] that during the aggregation, a large majority of oligomer structures are unstable and dissociate into their monomers instead of forming a new fibril structure, while the minority of the oligomers only convert into the fibril structure. Several research studies and hundreds of clinical trials since the early identification of the AD in 1906 have not been sufficient to discover an effective drug to alleviate the course of the AD disease [2], primarily due to the disordered nature of Aβ proteins that remains challenging for therapeutics.

2. Why Do Molecular Dynamics Simulations Cannot Accurately Quantify the Aβ Structural Ensemble?

Experimental studies have been unable to determine the properties of Aβ peptide in solution due to the fast conformational changes and enhanced aggregation tendency. These studies have produced time- and space-average results that are difficult to map into a conformational state of folded and unfolded proteins. Computational simulations can make a time series at the atomic level that could help us explore the protein structure, dynamics, misfolding and aggregation mechanism, becoming a particularly suitable complement to experimental studies of conformational changes of Aβ. Several force fields (FFs) to study biomolecules have been developed in the last decades, such as AMBER, GROMOS, OPLS families, namely AMBER94, AMBER96, AMBER99, AMBER99SBildn, AMBER03, AMBER12SB, AMBER14SB, CHARMM22*, CHARMM36, CHARMM36m, OPLS, GROMOS43a1, GROMOS43a2, GROMOS43a3, GROMOS53a5, GROMOS53a6 and GROMOS54a7. Most of the existing FFs describe phenomena associated with well-structured proteins. However, Saravanan et al. [11] concluded in a review study that the AMBER99SB-ILDN and CHARMM36m are highly optimized FFs and better choices for the characterization of IDPs such as Aβ peptide. This statement is supported because these FFs rendered the well agreement with experimental NMR chemical shift and β-sheet content, and the AMBER99SB-disp [12] force field is also worth considering for the same purpose.
Five recent FFs Amber ff14SB, Amber ff14SB_idps, Amber ff99SB, CHARMM36, CHARMM36m have been used by Pawel et al. [13] to explore the large conformational space of monomeric Aβ42 peptide during 10μs conventional molecular dynamics (MD) and 48 trajectories of replica exchange MD for 28.8μs. These FFs provided better results than their predecessor older versions. The potential energy can be described by Etotal = Ebonded + Enonbonded where the bonded term (Ebonded) consists of bond, angle, and dihedral-angle potentials, which explain the interactions of the atoms linked by covalent bonds, and the nonbonded term (Enonbonded) is constituted by van der Waals(vdW) and electrostatic interactions. The electrostatic and vdW components are the primary contribution to nonbonded energy for monomeric Aβ1-42. In the case of the CHARMM force field, the role of vdW interaction is reduced for Aβ1-42 peptide and enhanced for the Aβ1-42-water-ions interaction, whereas, in the case of Amber ff99SB, nonbonded potential energy slightly level up by the higher domination of electrostatic interaction, resulting in additional stabilization of the Aβ1-42 peptide related an over-structured β sheet. The interaction with water molecules contributes to the dynamics, misfolded and self-assembly of the Aβ peptide. The stronger solute-solvent interaction leads Aβ1-42 to be less stable and more hydrophilic. In addition, MD simulation studies with CHARMM36m and FF14SB_IDPs show antiparallel β-sheets between residues 16–21 and 29–36 of monomeric Aβ1-42, and short a β-strand in the C-terminal of the same monomer, which is in excellent agreement with NMR studies [14]. AMBER_ff14SB and AMBER_ff99SB overestimated α-helical and β-contents, respectively. Pawel et al. [13] strongly recommended using CHARMM36m force field for the study of the Aβ42-water-ion complex system over the AMBER FFs.
It is a big challenge to determine an accurate description of the structure of IDPs through MD simulations based only on FFs. In this perspective, Chong et al. [15] reviewed advanced computational methods that employ protein configuration entropy and render a thermodynamic connection between structural disorder and protein properties. For example, the CHARMM and OPLS FFs exhibit lower average β-sheet content in dimers of Aβ42 than that obtained with GROMOS 53a6 force field [15]. Subsequently, the average β-sheet content of the Aβ42 dimers was found to be greater in OPLSAA [16] than in AMBERFF99SB [17]. Interestingly, both AMBER99SB-ILDN and OPLS/L FFs have produced results of the average secondary structure of Aβ42 tetramer similar to each other [18].
The structural and thermodynamics properties of IDPs are susceptible to solute-solvent interaction compared to the folded protein. The choice of a reliable water model is necessary to characterize the Aβ42 peptide. Chong et al. [19] performed an MD simulation to investigate the structural properties of Aβ1-42 peptide by employing AMBER ff99SB force field with different solvent water models. They demonstrated that TIP4P-Ew exposed more Aβ1-42-water interaction than conventional TIP3P water model [15]. They strongly encouraged using the TIP4P-Ew water model to investigate the Aβ1-42 peptide structural properties. In a review, Chong et al. [15] reported that existing FFs are insufficient to expose Aβ protein to water. Recently, the same problem has been addressed by a couple of groups. The first group [20] opted to scale the Lennard-Jones potential between atoms in proteins and oxygen atoms in water by factor 1.1 without disturbing water-water and water-protein interaction. The second group [21] introduced a new water model, TIP4P-D, which included an additional parameter in the TIP4P water model to overcome the deficiencies in water dispersion interaction.
Recently developed FFs and their default water model are tabulated in Table 1. Rahman et al. [22] have evaluated the accuracy of recent developed FFs ff99IDPs, ff14IDPs, ff14IDPSFF, ff03w, CHARMM36m, and CHARMM22* by performing MD simulations for two short peptides (HEWL19 and RS), five IDPs (HIV-rev, Aβ40, Aβ421Z0Q, Aβ42model, and pdE-γ) and two folded proteins (CspTm and ubiquitin) using trajectories of 1, 1.5, 5 or 10 μs for each system. They have compared J-coupling between MD simulation and NMR experiment for folded and disordered protein using different FFs. The J-coupling (J3-HNH2 and J3-HαC) parameter measures the secondary structure distribution based on φ backbone dihedral angle. Three IDPs FFs, ff99IDPs, ff14IDPSFF, ff14IDPs were in good agreement with the experimental J-coupling constant compared with tested FFs ff03w, CHARMM36m, and CHARMM22*. The balance between the local structural property (NMR chemical shift) and global structural property (Rg) is still a challenging issue for molecular simulations of IDPs. Rahman et al., [22] noted two observations: (1) average Rg for Aβ421Z0Q is 12.1 Å which is in close agreement with experimental Rg 12.4 Å, while ff03w showed Rg equal to 10.53 Å and CHARMM36m displayed Rg about 13 Å, which suggests highly divergence among those FFs; (2) the three IDPs FFs render a good balance between secondary structures contents for both Aβ40 and Aβ42model. While Amberff03w, CHARMM36m and CHARMM22* overestimated the α-helical structure for IDPs, thus favouring folded protein structures. Therefore, the three specific IDPs FFs were developed by incorporating the changes made in the pre-existing FFs (Table 1) to enable an accurate description of the folded and misfolded proteins [12][23][24][25][26][27][28][29][30][31][32].
Table 1. Latest developed force field for intrinsically disordered protein and water model.
Force Field Parameter Set Developments Water Model Reference
AMBER ff99IDPs Updated from ff99SBildn by adding a set of backbone torsion parameters of eight disordered promoting amino acids. TIP3P Wei Y et al. [23] 2015
ff14IDPs Updated from ff14SB by embedding a set of backbone torsion parameters of eight disordered promoting amino acids. TIP3P Song et al. [25] 2017
ff14IDPSFF Updated from ff14SB by introducing a set of backbone torsion parameters for 20 amino acids TIP3P Song et al. [26] 2017
ff03CMAP Updated from ff03 by introducing a correction maps (CMAP)-optimized force field TIP4PD
(Modified the
dispersion interaction
of the TIP4P)		 Zhang et al. [27] 2019
ff14SB Updated from ff99SB by improving the Accuracy of Protein Side Chain and Backbone Parameters TIP3P Maier et al. [28] 2015
ff03w Updated from ff03 by adding slight backbone modification TIP4P/2005 Best et al. [29] 2010
A99SB_disp Update from a99SB-ILDN by an introducing small change in the protein and water vdW interaction terms TIP4P-D Robustelli et al. [12] 2018
CHARMM CHARMM36m Updated from CHARMM36 by a refined backbone correction map potential CHARMM-modified TIP3P Huang et al. [30] 2017
CHARMM36IDPSFF Updated from CHARMM36m by CMAP corrections made for all 20 naturally occurring amino acids CHARMM-modified TIP3P Liu H et al. [31] 2019
CHARMM22* Updated from CHARMM by introducing modifications in backbone torsion potential CHARMM-modified TIP3P Stefano Piana et al. [32] 2011
CHARMM36mW Van der Waals interaction between protein and water are included in CHARMM36m CHARMM-modified TIP3P Samantray et al. [24] 2020
The inconsistency of empirical physical models used in MD techniques can impact FFs and water models that affect the simulation result’s accuracy. Researchers have strived hard to develop perfect FFs to improve IDPs description; they aim to describe the high flexibility of these proteins, thus enlarging the conformational ensemble and increase the possibility of locating them in different local minima. Mu et al. [33] reported a couple of ideas to improve the accuracy of FFs for IDPs structural characterization, (1) Modification of force field parameters aided by global optimization, and (2) Maintaining a good balance between secondary structure via reparameterization (backbone dihedral parameters and vdW interaction between water-protein interaction) of existing FFs. One of the most common problems among the IDPs force field is over-stabilizing protein-protein interaction that impacts the aggregation mechanism of IDPs. Due to the IDPs force field’s inaccuracy, Mu et al. [33] encouraged improving backbone dihedral parameters and Lennard-Jones potential parameter (protein-water interaction) in the existing IDPs FFs and obtained training data from experimental observation and quantum chemical calculation. Undoubtedly, both reparameterization and training strategies may assist in new FFs development.
Another option to the atomistic FFs is to employ state-of-the-art coarse-grained (CG) models that not only sample more efficiently the entire space of protein conformations for large systems but also allow simulations for longer time scales of hundreds of µs [34], generally forbidden by brute force all-atom MD simulation and very relevant for biological processes [35] (e.g., folding, allosteric communications, conformational changes under mutations, self-assembly process, etc). Some popular CG FFs such as UNRES has been employed to study the fibril formations initiated by templates of Aβ40 fragments [36] capturing the dock-lock mechanism and similar the crowding effect of fragments was studied by PRIMO CG FF [37]. MARTINI 2 was employed to unveil the aggregation and organization of short Aβ16-22 peptides in lipid membranes [38]. The abovementioned CG FFs capture processes in time scales inaccessible atomic FFs, but yet they were restricted by system size or a lack of flexibility in secondary structure transitions. In this regard, the new release of MARTINI 3 force field aided by Gō-Like model [39][40][41][42] can become a new tool for realistic exploration of full-length Aβ peptide aggregation in contact with complex lipid-cholesterol membranes. Marrink group has made large efforts to develop a library of different lipid species (i.e., about 63 types) consistent with human plasma cells [43]. Following this idea, Poma et al. [44] have employed a very simplified CG model [45] to unveil the mechanical properties of Aβ40 and Aβ42 fibrils under different mechanical deformation process (e.g., tensile, indentation and shearing stresses) [46] and more recently they investigated [47] the change in mechanical stability between the oligomer and matured fibrils. The soluble oligomers are characterized by a length size about 3 to 5 nm, whereas Aβ fibrils typically reach hundreds of nm (see Figure 2). It is well-known the inverse relationship between toxicity and the length of the Aβ assembly [48]. Oligomers are considered more toxic than fibrils because of their high degree of flexibility toward low molecular weights, and the possibility of forming hydrophobic structures that may impair cell functions. Instead, fibrils are more thermodynamic stable and stiffer and less capable to undergo transitions to smaller and more toxic assemblies. Over the years, still some questions still remain open in terms of the mechanical characterization in amyloidogenesis and Aβ aggregate maturation: (a) what is the major role of the mechanical stability during Aβ oligomerization (e.g., tetramer, hexamer, etc)? (b) is the toxicity of oligomers which are closer to the membrane correlated by a minimum of mechanostability of Aβ peptide complexes, (c) how is the gain in mechanical stability from oligomers to fibrils involved in disease progression? and (d) Can we devise new strategies to reduce the mechanical stability of oligomer-to-fibril step through small molecular breakers (i.e., drugs recognition process)? To provide new answers to those open problems, new research combining versatile CG FFs and single molecule force spectroscopy is highly advised. For instance, in MD simulations, one can trace hydrophobic native interactions in equilibrium and simultaneously during a deformation process. Hence, the idea of hydrophobic structures can find support in molecular simulations as the main driving force for cell damage. Furthermore, molecular pathways could elucidate the critical conformation that maintains the mechanical stability of the Aβ assembly in the single-molecule force spectroscopy experiment. Figure 2 depicts the most relevant structure during aggregation and current methodologies used for its computational characterization [47][49].
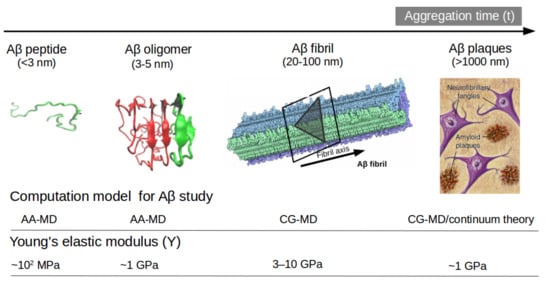
Ijms 22 10798 g002 550
Figure 2. Representation of Aβ structures during aggregation: (a) free Aβ peptide, (b) oligomers, (c) fibrils and (d) plaques. Typical lengths are given for peptide (<3 nm), oligomers (3–5 nm) and fibrils (20–100 nm). All-atom MD (AA-MD), coarse-grained MD (CG-MD) and continuum models have been employed to unveil the mechanical stability for each structure. Young modulus (Y) defined by the ratio of applied tensile stress to a given strain provides an idea of the elastic regime. Y values for each structure is taken from ref (50 and 51). Some images are modified with permission of BrightFocus Foundation.
Samantray et al. [32] have examined recently developed IDPs FFs, namely AMBER99SB-disp, CHARMM36m, and CHARMM36 with enhanced protein-water interactions (CHARMM36mW) for the study of Aβ16-22 (wildtype) aggregation and its mutation F19L Aβ16−22 (mutation 1) and F19 V/F20 V Aβ16−22 (mutation2), as model systems for testing purpose. In AMBER99-disp, the peptide-water interactions are increased too much resulting in an inhibition of the Aβ16-22 aggregation. The same trend has been observed in the simulation with the AMBERFF03w force field [50]. The difference between CHARMM36m and CHARMM36mW is a reparameterization of the protein-water interaction. In contrast, an experimental study [51] reported the following aggregation order mutation1>wildtype>mutation2≈0. AMBER99-disp does not apply for Aβ aggregation process because the interactions between peptide and water are drastically increased, leading to inhibition of the aggregation pathway. The CHARMM36mW can provide aggregation rate in the order of wildtype>mutation1>mutation2. Thus, FFs cannot reproduce the aggregation of Aβ peptide observed in experiments, but they maintain a better balance between peptide-water and peptide-peptide interaction. These results imply that improving the force field significantly impacted the simulation aggregation pathway than modifying the protein sequence. Samantray et al. [32] strongly encourage the use of CHARMM36mW for studying a full-length Aβ, even though it is not a perfect force field, since it yielded a promising result for aggregation benchmark. Nevertheless, reparameterization of this specific force field is still required.
Lockhart et al. [52] performed REMD simulations to examine the impact of the three popular FFs, CHARMM22 (protein FF) with CHARMM36 (lipid FF), CHARMM36m (protein FF) with CHARMM36 (lipid FF), and Amber14SB (protein FF) with Lipid14 (lipid FF), for the binding mechanism between the Aβ10-40 and the Dimyristoylgylcerophosphocholine (DMPC) bilayers. These three FFs have shown similar results in subjects like (a) stable helix formed in C-terminal of the peptide, (b) C-terminal of the peptide inserted into the bilayer hydrophobic core, (c) the thickness of the bilayer induced by the peptide about 10 Å and d) the disordered effect induced by the peptide on the fatty acid tails in the DMPC lipids. Nevertheless, these three FFs yielded different conformation ensembles of the peptide and bilayer that do not disturb the binding of the peptide with the bilayers.
Coskuner et al. [53] have reviewed several studies extensively and suggested that widely used FFs CHARMM, AMBER, GROMOS and OPLS, cannot produce accurate results for disordered entities. Even more, all existing computational techniques were designed to describe phenomena in ordered protein systems rather than in disordered protein structures. Important to mention that, Density Functional Theory (DFT) suffered from a number of errors that originated in the approximation of exchange-correlation functionals. These errors have been identified as the underestimation of barriers in describing chemical reactions, the band gaps, charge transfer excitation energies, and binding energies of charge transfer species in a biomolecule. DFT is the basis for constructing FFs such as CHARMM, AMBER, GROMOS and OPLS for intrinsically disordered protein and their complexes with ligands. These FFs are associated with an approximate exchange-correlation function that may lead to mistakes during prediction of the structural properties of IDPs. Notably, overcoming deficiencies of the exchange-correlation functional in DFT will help to improve the accuracy of IDP FFs.

References

  1. Alzheimer’s Association. 2021 Alzheimer’s Disease Facts and Figures. Alzheimer’s Dement. 2021, 17, 327–406.
  2. Hardy, J.A.; Higgins, G.A. Alzheimer’s Disease: The Amyloid Alzheimer’s Disease. Science 1992, 256, 184–185.
  3. Bai, X.C.; Yan, C.; Yang, G.; Lu, P.; Ma, D.; Sun, L.; Zhou, R.; Scheres, S.H.W.; Shi, Y. An Atomic Structure of Human γ-Secretase. Nature 2015, 525, 212–217.
  4. Colvin, M.T.; Silvers, R.; Ni, Q.Z.; Can, T.V.; Sergeyev, I.; Rosay, M.; Donovan, K.J.; Michael, B.; Wall, J.; Linse, S.; et al. Atomic Resolution Structure of Monomorphic Aβ42 Amyloid Fibrils. J. Am. Chem. Soc. 2016, 138, 9663–9674.
  5. Wälti, M.A.; Ravotti, F.; Arai, H.; Glabe, C.G.; Wall, J.S.; Böckmann, A.; Güntert, P.; Meier, B.H.; Riek, R. Atomic-Resolution Structure of a Disease-Relevant Aβ(1-42) Amyloid Fibril. Proc. Natl. Acad. Sci. USA 2016, 113, E4976–E4984.
  6. Gremer, L.; Schenk, C.; Reinartz, E.; Ravelli, R.B.G.; Tusche, M.; Lopez-iglesias, C.; Hoyer, W.; Heise, H.; Willbold, D. Fibril Structure of Amyloid-b (1-42) by Cryo–Electron Microscopy. Science 2017, 119, 116–119.
  7. Roberts, B.R.; Lind, M.; Wagen, A.Z.; Rembach, A.; Frugier, T.; Li, Q.X.; Ryan, T.M.; McLean, C.A.; Doecke, J.D.; Rowe, C.C.; et al. Biochemically-Defined Pools of Amyloid-β in Sporadic Alzheimer’s Disease: Correlation with Amyloid PET. Brain 2017, 140, 1486–1498.
  8. Kayed, R.; Head, E.; Thompson, J.L.; McIntire, T.M.; Milton, S.C.; Cotman, C.W.; Glabel, C.G. Common Structure of Soluble Amyloid Oligomers Implies Common Mechanism of Pathogenesis. Science 2003, 300, 486–489.
  9. O’Nuallain, B.; Wetzel, R. Conformational Abs Recognizing a Generic Amyloid Fibril Epitope. Proc. Natl. Acad. Sci. USA 2002, 99, 1485–1490.
  10. Michaels, T.C.T.; Šarić, A.; Curk, S.; Bernfur, K.; Arosio, P.; Meisl, G.; Dear, A.J.; Cohen, S.I.A.; Dobson, C.M.; Vendruscolo, M.; et al. Dynamics of Oligomer Populations Formed during the Aggregation of Alzheimer’s Aβ42 Peptide. Nat. Chem. 2020, 12, 445–451.
  11. Saravanan, K.M.; Zhang, H.; Zhang, H.; Xi, W.; Wei, Y. On the Conformational Dynamics of β-Amyloid Forming Peptides: A Computational Perspective. Front. Bioeng. Biotechnol. 2020, 8, 1–19.
  12. Robustelli, P.; Piana, S.; Shaw, D.E. Developing a Molecular Dynamics Force Field for Both Folded and Disordered Protein States. Proc. Natl. Acad. Sci. USA 2018, 115, E4758–E4766.
  13. Krupa, P.; Pham, D.Q.H.; Li, M.S. Properties of Monomeric Aβ42 Probed by Different Sampling Methods and Force Fields: Role of Energy Components. J. Chem. Phys. 2019, 151, 055101.
  14. Kirkitadze, M.D.; Condron, M.M.; Teplow, D.B. Identification and Characterization of Key Kinetic Intermediates in Amyloid β-Protein Fibrillogenesis. J. Mol. Biol. 2001, 312, 1103–1119.
  15. Chong, S.H.; Chatterjee, P.; Ham, S. Computer Simulations of Intrinsically Disordered Proteins. Annu. Rev. Phys. Chem. 2017, 68, 117–134.
  16. Viet, M.H.; Nguyen, P.H.; Derreumaux, P.; Li, M.S. Effect of the English Familial Disease Mutation (H6R) on the Monomers and Dimers of Aβ40 and Aβ42. ACS Chem. Neurosci. 2014, 5, 646–657.
  17. Huy, P.D.Q.; Vuong, Q.V.; La Penna, G.; Faller, P.; Li, M.S. Impact of Cu(II) Binding on Structures and Dynamics of Aβ42 Monomer and Dimer: Molecular Dynamics Study. ACS Chem. Neurosci. 2016, 7, 1348–1363.
  18. Nguyen, H.L.; Krupa, P.; Hai, N.M.; Linh, H.Q.; Li, M.S. Structure and Physicochemical Properties of the Aβ42 Tetramer: Multiscale Molecular Dynamics Simulations. J. Phys. Chem. B 2019, 123, 7253–7269.
  19. Chong, S.H.; Ham, S. Assessing the Influence of Solvation Models on Structural Characteristics of Intrinsically Disordered Protein. Comput. Theor. Chem. 2013, 1017, 194–199.
  20. Best, R.B.; Zheng, W.; Mittal, J. Balanced Protein-Water Interactions Improve Properties of Disordered Proteins and Non-Specific Protein Association. J. Chem. Theory Comput. 2014, 10, 5113–5124.
  21. Piana, S.; Donchev, A.G.; Robustelli, P.; Shaw, D.E. Water Dispersion Interactions Strongly Influence Simulated Structural Properties of Disordered Protein States. J. Phys. Chem. B 2015, 119, 5113–5123.
  22. Rahman, M.U.; Rehman, A.U.; Liu, H.; Chen, H.F. Comparison and Evaluation of Force Fields for Intrinsically Disordered Proteins. J. Chem. Inf. Model. 2020, 60, 4912–4923.
  23. Ye, W.; Ji, D.; Wang, W.; Luo, R.; Chen, H.F. Test and Evaluation of Ff99IDPs Force Field for Intrinsically Disordered Proteins. J. Chem. Inf. Model. 2015, 55, 1021–1029.
  24. Song, D.; Wang, W.; Ye, W.; Ji, D.; Luo, R.; Chen, H.F. Ff14IDPs Force Field Improving the Conformation Sampling of Intrinsically Disordered Proteins. Chem. Biol. Drug Des. 2017, 89, 5–15.
  25. Song, D.; Luo, R.; Chen, H.F. The IDP-Specific Force Field Ff14IDPSFF Improves the Conformer Sampling of Intrinsically Disordered Proteins. J. Chem. Inf. Model. 2017, 57, 1166–1178.
  26. Zhang, Y.; Liu, H.; Yang, S.; Luo, R.; Chen, H.F. Well-Balanced Force Field Ff03 CMAP for Folded and Disordered Proteins. J. Chem. Theory Comput. 2019, 15, 6769–6780.
  27. Maier, J.A.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.E.; Simmerling, C. Ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from Ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713.
  28. Best, R.B.; Mittal, J. Protein Simulations with an Optimized Water Model: Cooperative Helix Formation and Temperature-Induced Unfolded State Collapse. J. Phys. Chem. B 2010, 114, 14916–14923.
  29. Huang, J.; Rauscher, S.; Nawrocki, G.; Ran, T.; Feig, M.; De Groot, B.L.; Grubmüller, H.; MacKerell, A.D. CHARMM36m: An Improved Force Field for Folded and Intrinsically Disordered Proteins. Nat. Methods 2016, 14, 71–73.
  30. Liu, H.; Song, D.; Zhang, Y.; Yang, S.; Luo, R.; Chen, H.F. Extensive Tests and Evaluation of the CHARMM36IDPSFF Force Field for Intrinsically Disordered Proteins and Folded Proteins. Phys. Chem. Chem. Phys. 2019, 21, 21918–21931.
  31. Piana, S.; Lindorff-Larsen, K.; Shaw, D.E. How Robust Are Protein Folding Simulations with Respect to Force Field Parameterization? Biophys. J. 2011, 100, L47–L49.
  32. Samantray, S.; Yin, F.; Kav, B.; Strodel, B. Different Force Fields Give Rise to Different Amyloid Aggregation Pathways in Molecular Dynamics Simulations. J. Chem. Inf. Model. 2020, 60, 6462–6475.
  33. Mu, J.; Liu, H.; Zhang, J.; Luo, R.; Chen, H.F. Recent Force Field Strategies for Intrinsically Disordered Proteins. J. Chem. Inf. Model. 2021, 61, 1037–1047.
  34. Kmiecik, S.; Gront, D.; Kolinski, M.; Wieteska, L.; Dawid, A.E.; Kolinski, A. Coarse-Grained Protein Models and Their Applications. Chem. Rev. 2016, 116, 7898–7936.
  35. Seo, M.; Rauscher, S.; Pomès, R.; Tieleman, D.P. Improving Internal Peptide Dynamics in the Coarse-Grained MARTINI Model: Toward Large-Scale Simulations of Amyloid- and Elastin-like Peptides. J. Chem. Theory Comput. 2012, 8, 1774–1785.
  36. Rojas, A.; Maisuradze, N.; Kachlishvili, K.; Scheraga, H.A.; Maisuradze, G.G. Elucidating Important Sites and the Mechanism for Amyloid Fibril Formation by Coarse-Grained Molecular Dynamics. ACS Chem. Neurosci. 2017, 8, 201–209.
  37. Latshaw, D.C.; Cheon, M.; Hall, C.K. Effects of Macromolecular Crowding on Amyloid Beta (16-22) Aggregation Using Coarse-Grained Simulations. J. Phys. Chem. B 2014, 118, 13513–13526.
  38. Sahoo, A.; Xu, H.; Matysiak, S. Pathways of Amyloid-Beta Absorption and Aggregation in a Membranous Environment. Phys. Chem. Chem. Phys. 2019, 21, 8559–8568.
  39. Souza, P.C.T.; Alessandri, R.; Barnoud, J.; Thallmair, S.; Faustino, I.; Grünewald, F.; Patmanidis, I.; Abdizadeh, H.; Bruininks, B.M.H.; Wassenaar, T.A.; et al. Martini 3: A General Purpose Force Field for Coarse-Grained Molecular Dynamics. Nat. Methods 2021, 18, 382–388.
  40. Mahmood, M.I.; Poma, A.B.; Okazak, K.I. Optimizing Gō-MARTINI Coarse-Grained Model for F-BAR Protein on Lipid Membrane. Front. Mol. Biosci. 2021, 8, 1–10.
  41. Poma, A.B.; Cieplak, M.; Theodorakis, P.E. Combining the MARTINI and Structure-Based Coarse-Grained Approaches for the Molecular Dynamics Studies of Conformational Transitions in Proteins. J. Chem. Theory Comput. 2017, 13, 1366–1374.
  42. Poma, A.B.; Li, M.S.; Theodorakis, P.E. Generalization of the Elastic Network Model for the Study of Large Conformational Changes in Biomolecules. Phys. Chem. Chem. Phys. 2018, 20, 17020–17028.
  43. Ingólfsson, H.I.; Melo, M.N.; Van Eerden, F.J.; Arnarez, C.; Lopez, C.A.; Wassenaar, T.A.; Periole, X.; De Vries, A.H.; Tieleman, D.P.; Marrink, S.J. Lipid Organization of the Plasma Membrane. J. Am. Chem. Soc. 2014, 136, 14554–14559.
  44. Poma, A.B.; Guzman, H.V.; Li, M.S.; Theodorakis, P.E. Mechanical and Thermodynamic Properties of Aβ42, Aβ40, and α-Synuclein Fibrils: A Coarse-Grained Method to Complement Experimental Studies. Beilstein J. Nanotechnol. 2019, 10, 500–513.
  45. Chwastyk, M.; Bernaola, A.P.; Cieplak, M. Statistical Radii Associated with Amino Acids to Determine the Contact Map: Fixing the Structure of a Type i Cohesin Domain in the Clostridium Thermocellum Cellulosome. Phys. Biol. 2015, 12, 46002.
  46. Poma, A.B.; Chwastyk, M.; Cieplak, M. Elastic Moduli of Biological Fibers in a Coarse-Grained Model: Crystalline Cellulose and β-Amyloids. Phys. Chem. Chem. Phys. 2017, 19, 28195–28206.
  47. Poma, A.B.; Thu, T.T.M.; Tri, L.T.M.; Nguyen, H.L.; Li, M.S. Nanomechanical Stability of Aβ Tetramers and Fibril-like Structures: Molecular Dynamics Simulations. J. Phys. Chem. B 2021, 125, 7628–7637.
  48. Sengupta, U.; Nilson, A.N.; Kayed, R. The Role of Amyloid-beta oligomers in Toxicity, Propogation, and Immunotherapy. EBioMedicine 2016, 6, 42–49.
  49. Hall, C.M.; Moeendarbary, E.; Sheridan, G.K. Mechanobiology of the Brain in Ageing and Alzheimer’s Disease. Eur. J. Neurosci. 2021, 53, 3851–3878.
  50. Carballo-Pacheco, M.; Ismail, A.E.; Strodel, B. On the Applicability of Force Fields to Study the Aggregation of Amyloidogenic Peptides Using Molecular Dynamics Simulations. J. Chem. Theory Comput. 2018, 14, 6063–6075.
  51. Senguen, F.T.; Doran, T.M.; Anderson, E.A.; Nilsson, B.L. Clarifying the Influence of Core Amino Acid Hydrophobicity, Secondary Structure Propensity, and Molecular Volume on Amyloid-β 16-22 Self-Assembly. Mol. Biosyst. 2011, 7, 497–510.
  52. Lockhart, C.; Smith, A.K.; Klimov, D.K. Three Popular Force Fields Predict Consensus Mechanism of Amyloid β Peptide Binding to the Dimyristoylgylcerophosphocholine Bilayer. J. Chem. Inf. Model. 2020, 60, 2282–2293.
  53. Akbayraka, I.Y.; Caglayanb, S.I.; Ozcanb, Z.; Uverskyc, V.N.; Coskuner-Weberb, O. Current Challenges and Limitations in the Studies of Intrinsically Disordered Proteins in Neurodegenerative Diseases by Computer Simulations. Curr. Alzheimer Res. 2020, 17, 805–818.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Biophysics
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Subramanian Boopathi
,
Adolfo B. Poma
View Times: 641
Revisions: 2 times (View History)
Update Date: 27 Oct 2021
Table of Contents
    1000/1000
    Hot Most Recent
    ScholarVision Creations
    Feedback