Your browser does not fully support modern features. Please upgrade for a smoother experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Elena Niculina Dragoi | + 4653 word(s) | 4653 | 2021-09-28 08:13:19 | | | |
| 2 | Conner Chen | Meta information modification | 4653 | 2021-10-09 03:12:38 | | |
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Dragoi, E.N. Biologically inspired metaheuristics. Encyclopedia. Available online: https://encyclopedia.pub/entry/14890 (accessed on 12 March 2026).
Dragoi EN. Biologically inspired metaheuristics. Encyclopedia. Available at: https://encyclopedia.pub/entry/14890. Accessed March 12, 2026.
Dragoi, Elena Niculina. "Biologically inspired metaheuristics" Encyclopedia, https://encyclopedia.pub/entry/14890 (accessed March 12, 2026).
Dragoi, E.N. (2021, October 08). Biologically inspired metaheuristics. In Encyclopedia. https://encyclopedia.pub/entry/14890
Dragoi, Elena Niculina. "Biologically inspired metaheuristics." Encyclopedia. Web. 08 October, 2021.
Copy Citation
A metaheuristic is a high level, problem-independent framework that provides a series of steps and guidelines used to develop heuristic optimizers. Nowadays, the tendency is to use the term for both the general framework and for the algorithms built based on its rules. In the latest years, the literature has shown an increase in the number of proposals of new optimization metaheuristics and their improvements through step alterations, local search procedures or hybridizations.
metaheuristics
optimization
animal-inspired
exploration
exploitation
1. Source of Inspiration
In order to perform the current review, the main databases searched were: ScienceDirect (https://www.sciencedirect.com/, accessed on 6 August 2021), Web of Science (https://apps.webofknowledge.com/, accessed on 6 August 2021), Google Scholar (https://scholar.google.ro/, accessed on 6 August 2021), Springer Link (https://link.springer.com/, accessed on 6 August 2021) and IEEE Xplore Digital Library (https://ieeexplore.ieee.org/Xplore/home.jsp, accessed on 6 August 2021). The terms used in the search process were “metaheuristics”, “nature-inspired optimizers” and “bio-inspired algorithms”. The strategy to use both nature-inspired and bio-inspired terms is related to the fact that, in many works, there is not a clear distinction between the two and they are used to describe a variety of metaheuristics. Based on the identified sources, a drill down (study of the references used) and drill up approach (study of the papers citing a specific work) were applied in order to determine additional appropriate manuscripts. For the covered period, 283 algorithms were identified. Their distribution, based on the inspiration source, is presented in Figure 1.
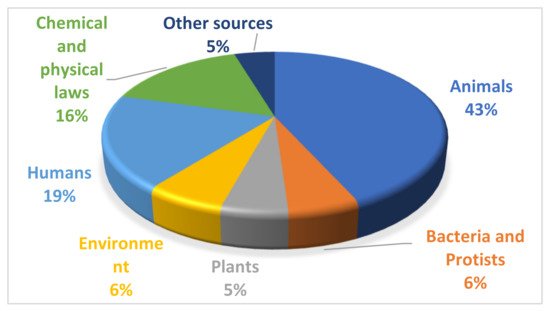
Figure 1. Distribution of newly proposed algorithms in the period 2006–2021, based on their inspiration source.
By analyzing the identified categories, two main groups can be distinguished: biological and non-biological sources. The biological sources include animals, plants and humans, while the non-biological sources are represented by the chemical and physical laws of nature. Therefore, broadly speaking, the optimization metaheuristics can be grouped into: (i) biologically-inspired and (ii) nature-inspired.
As it can be observed from Figure 1, the largest group of newly proposed metaheuristics in the considered period have animals as a source of inspiration, and this group is the main focus of the current work. Although humans, from a biological point of view, belong to the animal group, Chordata (vertebrates) phylum, in this work they were not included because they deserve a separate discussion, considering the unique ways of thinking, behaving and interacting with the environment.
In the latest years, various reviews have tried to shed light on the novel approaches that are constantly developed. Examples include: (i) a comprehensive list of algorithms and the steps of a few selected approaches [1]; (ii) a detailed discussion about the main research aspects specific to the field of nature-inspired metaheuristic optimizers [2].
2. Vertebrates
Most algorithms inspired by animals simulate two main general behaviors: (i) food search (foraging) and (ii) mating. For foraging, there are a number of theoretical models developed to predict the behavior of living things: the optimal foraging theory, the ideal free distribution, game theory and predator-prey models [3]. The theory of optimal foraging was developed to explain the dietary patterns and the resource use, and it states that the individuals using their energy more efficiently for finding food are favored by natural selection [4]. Foraging for food can be an individual activity (solitary foraging—where each individual searches for its food) or can be a social activity (social foraging—where foraging is a group behavior) [5]. The topics of social foraging include: (i) the mechanisms used by the members to find food; (ii) the manner in which the food locations are communicated to other members; (iii) the division of food between group members. The majority of foraging inspired optimization algorithms focus on the first two topics [5]. A taxonomy of foraging inspired algorithms is proposed in [6], where three main categories are identified: vertebrates (with backbone), invertebrates (without backbone) and non-neuronal (organisms that do not possess a central nervous system or brain).
Concerning the mating behavior, different theoretical models that simulate the mating mechanisms of specific species exist. For example, in birds, different strategies are used to display the quality of genes to the potential mates by showing the main physical features: color, shape of specific body parts, etc. In terms of partner combinations, five strategies are encountered: monogamy, polygyny, polyandry, parthenogenesis and promiscuity [7]. These mechanisms are included, in different forms, in the metaheuristic optimizers with the objective of improving diversity and thus increasing performance.
2.1. Birds
2.1.1 Mating Behavior
One of the best-known algorithms inspired from bird behavior is Cuckoo Search (CS) [8]. It simulates the brood parasitic behavior of some species of cuckoo and, in order to search for new solutions, it uses Levy flight random walk (mutation based on the best solution found so far) and biases/selective random walk (crossover between a current solution and its mutation) [9]. The Levy flight is a random process from the non-Gaussian class, a step which is based on the Levy distribution [10]. The steps of the CS algorithm express three idealized rules: (i) each cuckoo lays an egg and places it into a randomly chosen nest; (ii) the nests with high-quality eggs will be further used in the next generations; (iii) there is a fixed number of nests and there is a probability that the host will discover the foreign egg [11]. The main disadvantage of this algorithm is the fixed value of the scaling factor (that controls the step size) [9] and, in order to improve its performance, various strategies have been applied. A list of different modifications of CS and its applications can be found in [11][12]. Inspired by the same cuckoo breeding behavior, the Cuckoo Optimization Algorithm (COA) was proposed in [13]. When comparing COA and CS, it can be observed that COA is more complex, in the sense that it contains an additional behavioral aspect represented by the immigration process. Also, it uses the k-means clustering algorithm to identify the group that a cuckoo belongs to.
Bird Mating Optimizer (BMO) [7] uses the birds mating process as a framework. Throughout generations, the birds (the population of solutions) apply a probabilistic method to improve the quality of their offspring. The population is divided into males and females. The males can be monogamous, polygamous or promiscuous. On the other hand, the females can be parthenogenetic and polyandrous. In BMO, five species are simulated, and each one has its specific updating pattern.
Developed to adjust the parameters of adaptive neuro-fuzzy inference systems, the Satin Bowerbird Optimizer (SBO) [14] simulates the mating behavior of bowerbirds (a close relative species of the birds-of-paradise). In each iteration, a target individual is determined through roulette wheel selection. The other individuals try to follow it, i.e., they change their position accordingly, and try to improve their strategies by mutation.
2.1.2 Food Search
The flight of eagles (as does, in fact, the flight behavior of many animals and insects) has the typical characteristics of the Levy flight [15]. Based on this idea, the Eagle Strategy (ES) was proposed in [15]. It simulates an idealized two stage strategy (find and chase) [16]. The find step represents the exploration phase realized by the Levy walk and the chase step is an exploitation phase where an intensive local search is performed by the Firefly Algorithm (FA). ES represents a strategy and not an algorithm, and its authors indicate that different algorithms can be used at different stages of the iterations [17]. For example, in [17][18][19], Differential Evolution (DE) [20] performs the local search procedure that was initially solved by FA.
Chicken Swarm Optimization (CSO) is inspired by swarm behavior [21]. It mimics the flock and foraging behavior of chickens and is based on four simplified rules: (i) the swarm is comprised of several groups and each group has a dominant rooster, some hens and chicks; (ii) the selection of individuals representing each type of bird is based on the fitness value; (iii) the dominance and hen–chick relationship remains unchanged for several iterations; (iv) the search for food is performed around the dominant entity. CSO is a multi-swarm algorithm and its performance analysis showed that it can be efficiently applied to solve benchmarks and real-world problems.
The Crow Search Algorithm (CSA) [22] simulates the behavior of crows when it comes to food, i.e., storing excess food and thievery. Its main principles are: (i) crows live in flocks; (ii) each crow memorizes their hiding places; (iii) crows follow each other to steal food; (iv) crows try to protect their stashes. The algorithm includes a memory of good solutions and, since the movement of crows is performed regardless of whether a newly generated position is worse than the current one, distinctively from many metaheuristics, CSA is not a greedy algorithm.
Simulating the auditory-based hunting mechanism employed by owls, the Owl Search Algorithm (OSA) [23] assumes that the fitness value of each individual is correlated to the intensity of the received sound and that the search space has one global optimum.
The hummingbird’s optimization algorithm (HOA) [24] focuses on the foraging processes of hummingbirds. It includes a self-searching phase, based on the individual accumulated experience (using a Levy flight mechanism), and a guide-searching phase that includes information from dominant individuals.
Simulating the social roosting and foraging behavior of ravens, in [5], the Raven Roosting Optimization (RRO) is proposed. The algorithm includes four main components: (i) the perception capability of each individual to find food; (ii) a memory related to the position of previous foraging locations; (iii) transmitting and receiving information about food locations; (iv) probabilistic movement when searching for new resources.
Based on the cooperative hunting behavior of Harris hawks, the Harris Hawks Optimization (HHO) [25] algorithm simulates a series of aspects such as prey exploration, surprise pounce, and attack strategies. The algorithm complexity is O(population_size × (iterations + iterations × dimensionality + 1)) and, in exploring or exploiting the search space, a series of strategies such as diversification mechanism, progressive selection scheme and adaptive and time-varying parameters were used.
Aquila is a very successful bird of prey located in the Northern hemisphere that represents the source of inspiration for the Aquila Optimizer (AO) [26]. The model that the AO is based on simulates four hunting methods: (i) high soar with a vertical stoop (corresponding to an expanded exploration step); (ii) contour flight with glide attack (narrowed exploration step); (iii) low flight and slow descent (expanded exploitation step); (iv) walking and prey grabbing (narrowed exploitation). The AO computational complexity is O(solution_number × (iterations x dimensionality + 1)).
The hunting mechanisms of golden eagles (spiral trajectory for searching food and straight path when attacking, a tendency of cruising at the beginning of the search and attacking at the end, capability to easily change between cruising and attaching) is simulated in the Golden Eagle Optimizer (GEO) [27]. The attack phase corresponds to exploitation and cruising to exploration. To extend applicability, two variants were proposed: the GEO version (single objective) and the MOGEO (multi-objective) version. The GEO computational complexity is O(population_size × dimensionality × iterations) and that for MOGEO is O(population_size × dimensionality × iterations × objectives × archive).
2.1.4 Movement
Based on the characteristics of geese’s flight and the general PSO model, a geese-inspired hybrid PSO (Geese-PSO) was proposed in [28]. Although it does not use a completely novel metaphor and the algorithm is a hybridization, it is considered in this work because, to the authors’ knowledge, the principle of following the particle ahead and the application of a unidirectional flow of information was not used prior to the proposal of the Geese-PSO approach. In the same direction of research, Migrating Bird Optimization (MBO) [29] is inspired by the “V” flight formation of migrating birds. MBO is a neighborhood search approach where each solution is improved based on its neighbors.
The swarming behavior of passenger pigeons (the common name given to Blue Pigeons, Merne Rouck Pigeons, wandering long tailed Doves and Wood pigeons) represents the inspiration of the Pigeon Optimization Algorithm (POA) [30]. Pigeons have a specific behavior that can be simplified into a series of rules: (i) in order to enhance the search and reduce the probability of being prey for other animals, flight is performed in flocks; (ii) different flocks have their own solution for movement, which influences the shape of the group; (iii) there is communication between birds through “keck” and “tweet” calls; (iv) the behavior of other pigeons can be imitated; (v) the pigeons responding to the calls are the closest to the source of the call; (vi) in order to have a better probability of survival, each pigeon must lead. Another algorithm inspired by pigeons is Pigeon Inspired Optimization (PIO) [31]. However, in PIO the main idea is to simulate the homing behavior and the mechanisms used by a pigeon to move from a point A to a point B, i.e., orientation through magnetoreception and the sun, and recall of known landmarks close to the destination.
The migratory and attack behavior of seagulls is imitated in the Seagull Optimization Algorithm (SeOA) [32]. Several simplified rules are considered: (i) the migration is performed in groups; (ii) all the individuals travel towards the one with the best fitness; (iii) the attack follows a spiral-like movement. In addition, during the migration process, a mechanism for collision avoidance is included. The Sooty Tern Optimization Algorithm (STOA) [33] has a similar source of inspiration as the SeOA, but based on Sooty Tern seabirds. In this case, the migration behavior represents the exploration phase and the attacking behavior the exploitation one. The complexity of the STOA is O(problem_dimension × iteration × objective_number × population_size × objective_function) and the space complexity is O(objective_number × population_size).
In their fight to survive the harsh conditions of the polar regions, the emperor penguins use a specific strategy of huddling. This represents the main source of inspiration for the Emperor Penguin Optimizer (EPO) [34], where operations such as huddle boundary determination, temperature computation, distance determination and identification of the effective move are mathematically modeled and simulated in order to perform the optimization. The time complexity of EPO is O(k × individual_length × iterations × dimensionality × population_size), where the algorithm termination criteria requires O(k) time. The same mechanisms are also simulated in Emperor Penguins Colony (EPC) [35]. The main difference between the EPO and EPC consists in the manner in which the movement is realized, i.e., in EPC the individuals perform a spiral-like movement.
The foraging and navigation behaviors of African vultures is modeled in the African Vultures Optimization Algorithm (AVOA) [36], where multiple mechanisms to improve the exploration–exploitation balance were proposed: the use of a coefficient vector to change between these phases, use of phase-shift to precent premature convergence and local optimum escape and inclusion of Levy Flight. The AVOA computational complexity is based on initialization, fitness evaluation and vulture update and is O(iteration × population_size) + O(iteration × population_size × dimensionality).
2.2. Mammals
2.2.1 Food search
Based on the principles of echolocation used by bats to find food, the Bat Algorithm (BA) [37] employs several idealized rules: (i) echolocation is used for distance sensing and prey identification; (ii) the flying pattern is random, with characteristics such as velocity, pulse rate and loudness; (iii) the variation of loudness is assumed to move from a large value to a minimum (constant). The role of the pulse rate and loudness is to balance exploration and exploitation [38]. Another algorithm simulating bats is the Directed Artificial Bat Algorithm (DABA) [39]. DABA considers the individual flight of bats with no interaction between individuals, while in BA, the bat behavior is similar to the PSO particles. Although, compared to BA, the DABA model is closer to the natural behavior, in terms of optimization performance, BA is better [40]. On the other hand, the Dynamic Virtual Bats Algorithm (DVBA) [40] has a population comprised of only two individuals, i.e., explorer and exploiter bats, that dynamically exchange their roles based on their locations.
The echolocation mechanism is not specific to bats; other animals also using it to navigate and to find food, e.g., Dolphin Echolocation [41]. The abbreviation given by its authors is DE; however, so as not to confuse it with Differential Evolution, Dolphin Echolocation will be denoted by DEO in this work. It mimics the manner in which sound, in the form of clicks, is used to track and aim objects. Distinctively from the bat sonar system, which has a short range of 3–4 m, the range of the dolphin sonar varies from a few tens of meters to over a hundred meters. This aspect and the differences in the environmental characteristics lead to the development of totally different sonar systems, and a direct comparison between the two may be difficult.
In their search for food, sperm whales go as deep as 2000–3000 m and can stay underwater without breathing for about 90 min [42]. They are social animals, travel in groups and only the weaker specimens are attacked by predators such as orcas. This behavior was modeled in the Sperm Whale Algorithm (SWA) [42], where the population is divided into subgroups. In each cycle of breathing and feeding, the individual experiences two opposite poles (surface and bottom of the sea); however, because computing the mirror place is expensive and its influence on the search process is limited, it is applied only to the worst solutions. In order to simulate the hunting behavior of humpback whales, i.e., the bubble net feeding method, the Whale Optimization Algorithm (WOA) [43] searches for prey (the exploration phase) and then uses the shrinking encircling mechanism and the spiral updating position (the exploitation phase). A detailed review covering the multiple aspects of WOA is presented in [44].
The Grey Wolf Optimizer (GWO) [45] models a strict social dominant hierarchy and the group hunting mechanisms—tracking, chasing, approaching and attacking the prey–of grey wolfs (Canis lupus). The complexity of GWO is O(problem_dimension × iteration × objective_number × population_size × objective_function) [33]. Similar to other bio-inspired approaches, the GWO suffers from premature convergence. The prey weight and astrophysics concepts were applied in the Astrophysics Inspired Grey Wolf Optimizer (AGWO) [46] to simultaneously improve exploration and exploitation. Although wolves live in packs and communicate over long distances by howling, they have developed unique semi-cooperative characteristics [47]. By focusing on the independent hunting ability, as opposed to the GWO, which uses a single leader to direct the search in a cooperative manner, the Wolf Search Algorithm (WSA) [47] functions with multiple leaders swarming from multiple directions towards the optimal solution.
Spider monkeys are specific to South America and their behavior falls in the category of fission–fusion social structure [48], i.e., based on the scarcity or availability of food, they split from large to smaller groups and vice versa. The algorithm that simulates this structure is called Spider Monkey Optimization (SMO) [48]. It consists of six phases and, unlike the natural system, the position of leader (local or global) is not fixed, depending instead on its ability to search for food. In addition, the optimization procedure does not include the communication tactics specific to spider monkeys. Distinctively, the individual intelligence of chimps used for group hunting is modelled into the Chimp Optimization Algorithm (ChOA), where four types of hunting are included: driving, chasing, blocking and attacking [49]. Another type of ape is represented by gorillas and, in the Artificial Gorilla Troops Optimizer (GTO), their collective life is mathematically modeled to include exploration–exploitation mechanisms [50].
Spotted hyenas have a behavior similar to that of wolves and whales, which uses collective behavior to encircle the prey and attack. Their model is used in the Spotted Hyena Optimizer (SHO) [51], which saves the best-so-far solution, simulates the encircling prey through a circle-shaped neighborhood that can be extended to higher dimensions and controls the exploration–exploitation balance through control parameters. The time complexiy of SHO is O(problem_dimension × G × iteration × objective_number × population_size × objective_function), where the time to define the groups of individuals is O(G).
In the Squirrel Search Algorithm (SSA) [52], the gliding behavior of flying squirrels when exploring different areas of a forest in search for food is simulated by considering some simplifications of the natural mechanisms: (i) a squirrel is assumed to be on one tree; (ii) in the forest there are only three types of trees: normal, oak and hickory; (iii) the region under consideration contains three oaks and one hickory tree. It is considered that the squirrel with the best fitness is positioned on a hickory tree and the next three individuals with the best fitness are on oak trees. The other individuals in the population move towards the oak or the hickory, depending on their daily energy requirements. In SSA, the seasonal changes are modeled through control parameters and influence the behavior of the individuals in the population.
2.2.2 Social Behavior
The Lion’s Algorithm (LA) [53] is based on the social behavior of lions. It simulates the process of pride forming through mating, removing weak cubs, territorial defense and takeover. The population is formed of males and females and the cub population is subjected to gender grouping (through the application of k-means clustering). LA is not the only approach inspired by lions; the Lion Optimization Algorithm (LOA) [54] is also an example. Distinctively from LA, LOA includes the hunting and migration mechanisms and the mating process is based on differentiation rather than on crossover and mutation. Another lion-inspired approach is the Lion Pride Optimization (LPOA) [55].
Similar to honey bees or ant colonies, blind naked mole rats (a species specific to Africa) have a complex social behavior: (i) they live in large colonies; (ii) a queen and a reduced number of males are responsible for offspring generation; (iii) there are individuals specialized in food search and domestic activities, i.e., taking care of the nest and of the young and in protection against invaders [56]. These mechanisms, in a simplified form, are simulated in the Blind Naked Mole Rats (BNMR) algorithm [56].
Elephants are the largest walking mammals and their successful survival is influenced, among other things, by their social and behavioral structures. The adult males solitarily roam into the wild, they do not commit to any family and can potentially mate over thirty times a year, while the female elephants form matriarchal societies that allow better protection and safe rearing of young calves. The Elephant Search Algorithm (ESA) [57] and Elephant Herding Optimization [58][59] simulate these mechanisms and perform the search.
2.3. Other Vertebrates
This category includes other sources of inspiration from the vertebrate group that do not belong to the bird and mammal classes.
The SailFish Optimizer (SFO) [60] is inspired by the group hunting of sailfish (Istiophorus platypterus), one of the fastest fish in the ocean. This mechanism of alternating attacks on schools of sardines is modeled through the use of energy-based approaches, where, at the beginning of the hunt, both the predator and the prey are energetic and not injured; however, as the hunt continues, the power of the sailfish will decrease and the sardines will become tired and have reduced awareness.
The food catching behavior of Agama lizards is modelled in the Artificial Lizard Search Optimization (ALSO) [61]. The algorithm focuses on new discoveries regarding the mechanisms for movement control through the tail during prey hunting.
The manner in which chameleons catch prey using their long and sticky tongue represents the basis for the Chameleon Swarm Algorithm [62]. The notation given by the authors of this algorithm is CSA, however, since the same notation is used to represent the Crow Search Algorithm, in this work, the Chameleon Swarm Algorithm will be indicated by the ChSA notation. The ChSA follows three main strategies for catching prey: tracking (modelled as a position update step), eye pursuing (modeled as position update in accordance with the position of the prey) and attacking (based on tongue velocity). Distinctively from the majority of metaheuristics, which tend to have less than three parameters, ChSA has five parameters that help in controlling the exploration–exploitation balance.
2.4. General
Unlike the other algorithms mentioned in this work that have a source of inspiration represented by a single animal, in the case of the general class, the metaheuristics are based on a general aspect that can be specific to multiple animals or types of animals. Examples proposed prior to 2008 include algorithms such as Genetic Algorithms (where the genetic principles of mutation and crossover are applicable to all species) and Extremal Optimization [63], based on the Bak–Sneppen mechanism, a model of co-evolution between interacting species which reproduces nontrivial features of paleontological data.
Inspired from the encircling mechanisms used by group hunters such as lions, wolves and dolphins, the Hunting Search (HuS) [64] simulates the cooperation of members to catch food. As a perfect correlation between nature and an optimization process cannot be achieved, a set of differences from the real world are taken into account: (i) in the majority of cases, the location of the optimum of a problem is not known, while, in the real world, the hunters can see the prey or sense its presence; (ii) the optimum is set, however, in the real world, the prey dynamically changes its position. Unlike the DEO and GWO, which emulate the specific hunting approaches used by dolphins and wolves, HuS is focused on the cooperation aspect and the repositioning during the hunt. Other approaches which simulate the food searching mechanisms include: the Backtracking Search Algorithm Optimization (BSA) [65], Optimal Foraging Algorithm (OFA) [4], Fish Electrolocation Optimization (FEO) [66] and Marine Predators Algorithm (MPA) [67]. BSA is based on the return of a living creature to previously found fruitful areas. At its core, it is an evolutionary approach that, although it has a very similar structure to the other EAs, differs as follows: (i) mutation is applied to a single individual; (ii) there is a more complex crossover strategy compared with DE; (iii) it is a dual population algorithm; (iv) it has boundary control mechanisms. Distinctively from the BSA, the OFA algorithm is based on the Optimal Foraging Theory developed to explain the dietary patterns of animals. In the OFA, the animal foraging is an individual and its position represents a solution. Its time complexity is O(group_size × dimensionality × iterations) and its space complexity is O(group_size × dimensionality × (iterations + 1)). The FEO simulates the active and passive electrolocation mechanisms used by sharks and “elephant nose fishes” to find prey. A series of electric waves are generated and reflected back to the fish after hitting the surrounding objects, which creates an electric image that is then analyzed. In the case of the MPA, the different strategies used for finding food and the interaction between predator and prey are modeled in different scenarios through Brownian and Levy strategies. The MPA algorithm complexity is O(iterations × (agent_number × dimensionality + Cost_function_evaluation × agent_number)).
Another aspect specific to all species in their quest to survive is represented by the competition for food, resources or mates. Two metaheuristic optimizers based on competition were identified: Competition over Resources (COR) [68] and the Competitive Optimization Algorithm (COOA) [69]. The COR algorithm mimics the competition for food of wild animals. The groups with the best approach to storing food have improved scores while the worst performance groups are starving and, after a few generations, die and are removed from the population. In the COOA approach, the competition is simulated by the Imperialist Competitive Algorithm [70] and the groups are represented by the populations of various metaheuristics.
Migration behavior is encountered in all major animal groups. Among the first bio-inspired metaheuristics that contain elements specific to migration is the Biogeography-based Optimization (BBO) [71]. However, the BBO imitates a much larger phenomenon—island biogeography—that includes both migration and mutation [72]. Another algorithm that has the migration principle at its core is the Migrating Birds Optimization [29]. As it simulates the features of the “V” flight of birds, the MBO was included in the bird inspired metaheuristic section. The Animals Migration Optimization (AMO) [73] simulates the animal migration model proposed by ecologists and uses two idealized assumptions: (i) the leader animal will survive to the next generation; (ii) the number of animals in the population is fixed. The algorithm has two phases: the migration process (where the individuals respect three rules: move in the same direction as the neighbors, remain close to the neighbors and avoid collision with neighbors) and population update (where some individuals leave the group and others join it).
References
- Fausto, F.; Reyna-Orta, A.; Cuevas, E.; Andrade, G.; Perez-Cisneros, M. From ants to whales: Metaheuristics for all tastes. Artif. Intell. Rev. 2019, 53, 753–810.
- Hussain, K.; Salleh, M.N.M.; Cheng, S.; Shi, Y. Metaheuristic research: A comprehensive survey. Artif. Intell. Rev. 2018, 52, 2191–2233.
- Brabazon, A.; McGarraghy, S. Formal Models of Foraging. In Foraging-Inspired Optimisation Algorithms; Brabazon, A., McGarraghy, S., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 23–44.
- Zhu, G.-Y.; Zhang, W.-B. Optimal foraging algorithm for global optimization. Appl. Soft Comput. 2017, 51, 294–313.
- Brabazon, A.; Cui, W.; O’Neill, M. The raven roosting optimisation algorithm. Soft Comput. 2015, 20, 525–545.
- Brabazon, A.; McGarraghy, S. Introduction to Foraging-Inspired Algorithms. In Foraging-Inspired Optimisation Algorithms; Brabazon, A., McGarraghy, S., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 87–101.
- Askarzadeh, A. Bird mating optimizer: An optimization algorithm inspired by bird mating strategies. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 1213–1228.
- Yang, X.-S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), IEEE, Coimbatore, India, 9–11 December 2009.
- Wang, L.; Yin, Y.; Zhong, Y. Cuckoo search with varied scaling factor. Front. Comput. Sci. 2015, 9, 623–635.
- Chawla, M.; Duhan, M. Levy Flights in Metaheuristics Optimization Algorithms—A Review. Appl. Artif. Intell. 2018, 32, 802–821.
- Rakhshani, H.; Rahati, A. Snap-drift cuckoo search: A novel cuckoo search optimization algorithm. Appl. Soft Comput. 2017, 52, 771–794.
- Joshi, A.; Kulkarni, O.; Kakandikar, G.; Nandedkar, V. Cuckoo Search Optimization—A Review. Mater. Today Proc. 2017, 4, 7262–7269.
- Rajabioun, R. Cuckoo Optimization Algorithm. Appl. Soft Comput. 2011, 11, 5508–5518.
- Moosavi, S.H.S.; Bardsiri, V.K. Satin bowerbird optimizer: A new optimization algorithm to optimize ANFIS for software development effort estimation. Eng. Appl. Artif. Intell. 2017, 60, 1–15.
- Yang, X.S.; Deb, S. Eagle strategy using Levy walk and firefly algorithms for stochastic optimization. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); Springer: Berlin/Heidelberg, Germany, 2010; pp. 101–111.
- Yang, X.-S. Nature-inspired metaheuristic algorithms; Luniver press: Bristol, UK, 2010.
- Yang, X.-S.; Deb, S. Two-stage eagle strategy with differential evolution. Int. J. Bio-Inspired Comput. 2012, 4, 1–5.
- Gandomi, A.H.; Yang, X.-S.; Talatahari, S.; Deb, S. Coupled eagle strategy and differential evolution for unconstrained and constrained global optimization. Comput. Math. Appl. 2012, 63, 191–200.
- Talatahari, S.; Gandomi, A.H.; Yang, X.-S.; Deb, S. Optimum design of frame structures using the Eagle Strategy with Differential Evolution. Eng. Struct. 2015, 91, 16–25.
- Storn, R.; Price, K. Differential evolution—A simple and efficient adaptive scheme for global optimization over continuous spaces. J. Glob. Optim. 1995, 11, 341–359.
- Meng, X.; Liu, Y.; Gao, X.; Zhang, H. A New Bio-inspired Algorithm: Chicken Swarm Optimization. In Advances in Swarm Intelligence, Pt1; Tan, Y., Shi, Y., Coello, C.A.C., Eds.; Springer: Cham, Switzerland, 2014; pp. 86–94.
- Askarzadeh, A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comput. Struct. 2016, 169, 1–12.
- Jain, M.; Maurya, S.; Rani, A.; Singh, V. Owl search algorithm: A novel nature-inspired heuristic paradigm for global optimization. J. Intell. Fuzzy Syst. 2018, 34, 1573–1582.
- Zhuoran, Z.; Changqiang, H.; Hanqiao, H.; Shangqin, T.; Kangsheng, D. An optimization method: Hummingbirds optimization algorithm. J. Syst. Eng. Electron. 2018, 29, 386–404.
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Futur. Gener. Comput. Syst. 2019, 97, 849–887.
- Abualigah, L.; Yousri, D.; Elaziz, M.A.; Ewees, A.A.; Al-Qaness, M.A.; Gandomi, A.H. Aquila Optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 10725.
- Mohammadi-Balani, A.; Nayeri, M.D.; Azar, A.; Taghizadeh-Yazdi, M. Golden eagle optimizer: A nature-inspired metaheuristic algorithm. Comput. Ind. Eng. 2020, 152, 107050.
- Sun, J.; Lei, X. Geese-inspired hybrid particle swarm optimization algorithm for traveling salesman problem. In Proceedings of the 2009 International Conference on Artificial Intelligence and Computational Intelligence, IEEE, Shanghai, China, 7–8 November 2009.
- Duman, E.; Uysal, M.; Alkaya, A.F. Migrating Birds Optimization: A new metaheuristic approach and its performance on quadratic assignment problem. Inf. Sci. 2012, 217, 65–77.
- Goel, S. Pigeon Optimization Algorithm: A Novel Approach for Solving Optimization Problems. In Proceedings of the 2014 International Conference on Data Mining and Intelligent Computing (Icdmic), IEEE, Delhi, India, 5–6 September 2014.
- Duan, H.; Qiao, P. Pigeon-inspired optimization: A new swarm intelligence optimizer for air robot path planning. Int. J. Intell. Comput. Cybern. 2014, 7, 24–37.
- Dhiman, G.; Kumar, V. Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems. Knowl. Based Syst. 2018, 165, 169–196.
- Dhiman, G.; Kaur, A. STOA: A bio-inspired based optimization algorithm for industrial engineering problems. Eng. Appl. Artif. Intell. 2019, 82, 148–174.
- Dhiman, G.; Kumar, V. Emperor penguin optimizer: A bio-inspired algorithm for engineering problems. Knowl. Based Syst. 2018, 159, 20–50.
- Harifi, S.; Khalilian, M.; Mohammadzadeh, J.; Ebrahimnejad, S. Emperor Penguins Colony: A new metaheuristic algorithm for optimization. Evol. Intell. 2019, 12, 1–16.
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. Comput. Ind. Eng. 2021, 158, 107408.
- Yang, X.S. A New Metaheuristic Bat-Inspired Algorithm. Nicso 2010 Nat. Inspired Coop. Strateg. Optim. 2010, 284, 65–74.
- Addi, N.S.; Abdullah, S.; Hamdan, A.R. Multi-population cooperative bat algorithm-based optimization of artificial neural network model. Inf. Sci. 2015, 294, 628–644.
- Rekaby, A. Directed Artificial Bat Algorithm (DABA)-A new bio-inspired algorithm. In Proceedings of the 2013 International Conference on Advances in Computing, Communications and Informatics (ICACCI), IEEE, Mysore, India, 22–25 August 2013.
- Topal, A.O.; Altun, O. A novel meta-heuristic algorithm: Dynamic Virtual Bats Algorithm. Inf. Sci. 2016, 354, 222–235.
- Kaveh, A.; Farhoudi, N. A new optimization method: Dolphin echolocation. Adv. Eng. Softw. 2013, 59, 53–70.
- Ebrahimi, A.; Khamehchi, E. Sperm whale algorithm: An effective metaheuristic algorithm for production optimization problems. J. Nat. Gas Sci. Eng. 2016, 29, 211–222.
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67.
- Gharehchopogh, F.S.; Gholizadeh, H. A comprehensive survey: Whale Optimization Algorithm and its applications. Swarm Evol. Comput. 2019, 48, 1–24.
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61.
- KKumar, V.; Kumar, D. An astrophysics-inspired Grey wolf algorithm for numerical optimization and its application to engineering design problems. Adv. Eng. Softw. 2017, 112, 231–254.
- Fong, S.; Deb, S.; Yang, X.-S. A heuristic optimization method inspired by wolf preying behavior. Neural Comput. Appl. 2015, 26, 1725–1738.
- Bansal, J.C.; Sharma, H.; Jadon, S.S.; Clerc, M. Spider Monkey Optimization algorithm for numerical optimization. Memetic Comput. 2014, 6, 31–47.
- Khishe, M.; Mosavi, M.R. Chimp optimization algorithm. Expert Syst. Appl. 2020, 149, 113338.
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. Artificial gorilla troops optimizer: A new nature-inspired metaheuristic algorithm for global optimization problems. Int. J. Intell. Syst. 2021, 36, 5887–5958.
- Dhiman, G.; Kumar, V. Spotted hyena optimizer: A novel bio-inspired based metaheuristic technique for engineering applications. Adv. Eng. Softw. 2017, 114, 48–70.
- Jain, M.; Singh, V.; Rani, A. A novel nature-inspired algorithm for optimization: Squirrel search algorithm. Swarm Evol. Comput. 2019, 44, 148–175.
- Rajakumar, B.R. The Lion’s Algorithm: A New Nature-Inspired Search Algorithm. Procedia Technol. 2012, 6, 126–135.
- Yazdani, M.; Jolai, F. Lion Optimization Algorithm (LOA): A nature-inspired metaheuristic algorithm. J. Comput. Des. Eng. 2015, 3, 24–36.
- Kaveh, A.; Mahjoubi, S. Lion Pride Optimization Algorithm: A meta-heuristic method for global optimization problems. Sci. Iran. 2018, 25, 3113–3132.
- I Mohammad, T.M.H.; Mohammad, H.B.; Shirzadi, M.T.M.H.; Bagheri, M.H. A novel meta-heuristic algorithm for numerical function optimization: Blind, naked mole-rats (BNMR) algorithm. Sci. Res. Essays 2012, 7, 3566–3583.
- Deb, S.; Fong, S.; Tian, Z. Elephant search algorithm for optimization problems. In Proceedings of the 2015 Tenth International Conference on Digital Information Management (ICDIM), IEEE, Jeju, Korea, 21–23 October 2015.
- Wang, G.G.; Deb, S.; Coelho, L.D.S. Elephant Herding Optimization. In Proceedings of the 2015 3rd International Symposium on Computational and Business Intelligence, IEEE, Bali, Indonesia, 7–9 December 2015.
- Wang, G.G.; Deb, S.; Gao, X.Z.; Coelho, L.D.S. A new metaheuristic optimisation algorithm motivated by elephant herding behaviour. Int. J. Bio-Inspired Comput. 2016, 8, 394.
- Shadravan, S.; Naji, H.; Bardsiri, V. The Sailfish Optimizer: A novel nature-inspired metaheuristic algorithm for solving constrained engineering optimization problems. Eng. Appl. Artif. Intell. 2019, 80, 20–34.
- Kumar, N.; Singh, N.; Vidyarthi, D.P. Artificial lizard search optimization (ALSO): A novel nature-inspired meta-heuristic algorithm. Soft Comput. 2021, 25, 6179–6201.
- Braik, M.S. Chameleon Swarm Algorithm: A bio-inspired optimizer for solving engineering design problems. Expert Syst. Appl. 2021, 174, 114685.
- Boettcher, S.; Percus, A. Nature’s way of optimizing. Artif. Intell. 2000, 119, 275–286.
- Oftadeh, R.; Mahjoob, M.; Shariatpanahi, M. A novel meta-heuristic optimization algorithm inspired by group hunting of animals: Hunting search. Comput. Math. Appl. 2010, 60, 2087–2098.
- Civicioglu, P. Backtracking Search Optimization Algorithm for numerical optimization problems. Appl. Math. Comput. 2013, 219, 8121–8144.
- Haldar, V.; Chakraborty, N. A novel evolutionary technique based on electrolocation principle of elephant nose fish and shark: Fish electrolocation optimization. Soft Comput. 2016, 21, 3827–3848.
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377.
- Mohseni, S.; Gholami, R.; Zarei, N.; Zadeh, A.R. Competition over resources: A new optimization algorithm based on animals behavioral ecology. In Proceedings of the 2014 International Conference on Intelligent Networking and Collaborative Systems (INCoS), Salerno, Italy, 10–12 September 2014.
- Sharafi, Y.; Khanesar, M.A.; Teshnehlab, M. COOA: Competitive optimization algorithm. Swarm Evol. Comput. 2016, 30, 39–63.
- Atashpaz-Gargari, E.; Lucas, C. Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition. In Proceedings of the IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007.
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713.
- Niu, Q.; Zhang, L.; Li, K. A biogeography-based optimization algorithm with mutation strategies for model parameter estimation of solar and fuel cells. Energy Convers. Manag. 2014, 86, 1173–1185.
- Li, X.; Zhang, J.; Yin, M. Animal migration optimization: An optimization algorithm inspired by animal migration behavior. Neural Comput. Appl. 2013, 24, 1867–1877.
More
Information
Contributor
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
1.4K
Revisions:
2 times
(View History)
Update Date:
09 Oct 2021
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No





