Energy Management Systems for Microgrids

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Danny Espín-Sarzosa	+ 4111 word(s)	4111	2021-09-17 05:13:29	\|
2	format correct	Bruce Ren	-13 word(s)	4098	2021-09-26 03:58:46	\|

This entry is adapted from the peer-reviewed paper 10.3390/en13030547

Energy Management Systems (EMS) play a key role in the operation of a microgrids (MGs). In this context, this article presents both an extensive literature review and a qualitative and quantitative study to establish the main trends in the field of centralized EMS for MGs. EMS attributes for several features such as objective functions, resolution techniques, operating models, integration of uncertainties, optimization horizons, and modeling detail levels are considered for main trend identification. The main contribution of this study is the identification of four specific existing research trends: (i) dealing with uncertainties (comprises 33% of the references), (ii) multi-objective strategy (29%), (iii) traditional paradigm (21%), and (iv) P-Q challenge (17%). Each trend is described and analyzed based on the main drive of these separate research fields. The key challenges and the way to cope with them are described based on the rationality of each trend, the results of previous reviews, and the previous experience of the authors. Overall, finding these main trends, together with a complete paper database and their features, serve as a useful outcome for a better understanding of the current research-specific challenges, opportunities, potential barriers, and open questions regarding the creation of future centralized EMS developments.

microgrid energy management system centralized control architecture review research trends clustering

1. Introduction

In a microgrid (MG), energy management systems are recognized as control-essential elements in terms of stability, security, and efficiency, as well as power balancing elements in terms of their dependence on operating conditions variability, characterized by the uncertainty caused by power supplies from renewable energy resources (RES) and/or the dynamic behavior of electricity demand. In recent years, literature exhibited a new generation of energy management systems (EMS) approaches for MGs, which aim at dealing with the management of energy in variable operating and technological contexts. However, power flow control and the guarantee of highly reliable and stable MGs are becoming progressively complex ^[1]. Optimizing the size of the components and adopting an EMS strategy are essential to decreasing the cost of the system and limiting its negative effects ^[2].

A MG is defined as a self-contained electrical power system consisting of distributed energy resources (DERs), such as distributed generators (DG) and energy storage systems (ESS), and loads (controllable loads in some cases). All the above are considered as a single controllable system ^[3]^[4]. An MG can operate in either grid-connected ^[5]^[6]^[7]^[8]^[9]^[10]^[11]^[12] or isolated mode ^[13]^[14]^[15]^[16]^[17]^[18]^[19]^[20]^[21] or both ^[22]. The presence of more than one DER requires energy flow control from various sources to ensure reliable energy supply, safety, and a minimum-cost operation. Decisions on MGs are made by the EMS. In this sense, EMS are control devices responsible for defining the optimum scheduling of dispatchable units in an MG ^[23] by using different information about the latter, such as demand forecasting, power generation, energy storage, weather forecasts, energy grid prices, etc. ^[20]. An EMS can be classified by adopting a top-down approach, starting from general principles and down to developing specific processes models. Consequently, EMS can be classified at the top-level based on whether they have a centralized or decentralized control architecture.

In a centralized control architecture, the main responsibility for MG value maximization and the optimization of its operation lies with the EMS/Central controller ^[24], as shown in Figure 1a. In this figure, the red dashed arrows represent the exchange of information (centralized control communication) among local controllers and the EMS/Central controller, while the solid black arrows refer to the exchanged information (local control communication) among MG agents and their local controllers. The EMS uses inputs (weather forecast, load demand, SoC, energy prices, etc.) to perform scheduling and optimization procedures to determine the optimal set points for distributed generation (DG) loads and local controllers (LCs) in the MG.

Figure 1. (a) Centralized control architecture, (b) Decentralized control architecture.

On the other hand, a decentralized control architecture is shown in Figure 1b. In this figure, the blue dotted arrow represents the communication channel that allows local controllers/leaders to exchange information among them (decentralized control communication), and the black solid arrows, as in Figure 1a, represent the exchanged information among the local controller/leader and either other local controllers or MG agents. Each agent or group of agents is self-controlled or controlled by a leader, respectively ^[25]. For that reason, LC4a and LC4b are managed by LC4/Leader, and LC1, LC2, and LC3 are self-controlled; they can also exchange information among them. The main responsibility is given to competing or collaborating with LCs to optimize their production in order to satisfy the demand and probably provide the possible maximum export to the grid, considering current market prices ^[24]. A decentralized controller needs a complete local information to run the required control actions without full awareness of all system parameters ^[26], i.e., a decentralized approach is mainly based on a local measurement of parameters, such as voltage and frequency values ^[27]. Control actions are sent to the multiple DER and controllable loads. It is worth nothing that the peer-to-peer control concept ^[28] can be understood as part of the blue dotted line in Figure 1b.

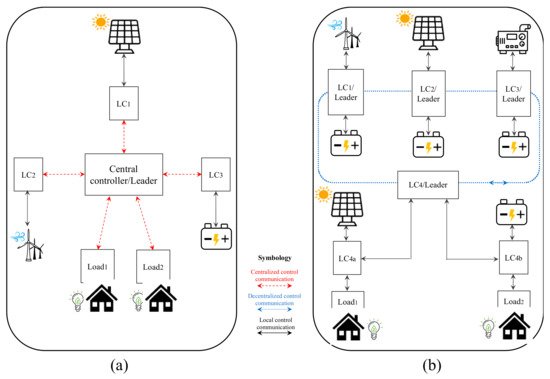
2. Attributes and Trends

2.1. Quantitative Results (Numerical Results Analysis)

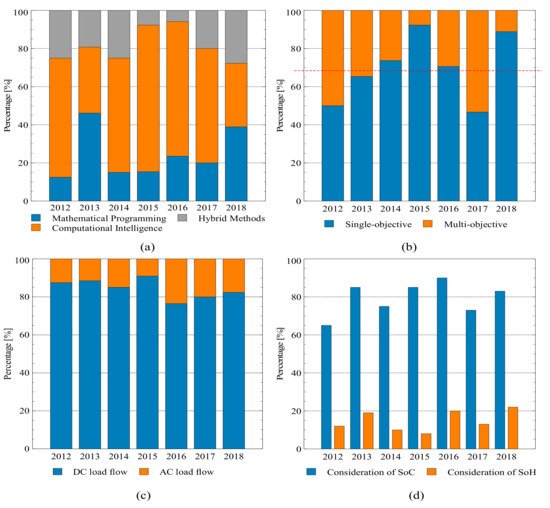
Figure 2a shows the distribution of the “resolution techniques” (percentages) used in recent years. The results show that, in general, CI techniques have been used with a higher frequency. Regarding MP approaches, despite MP ability to guarantee global optimal solutions, these have been considered to have a lower frequency than CI techniques. Finally, HM appear as an option to solve the EMS optimization problem. Based on the increasing complexity and new requirements for MG operations (cost-effectiveness, reliability, and resilience), HM may gain strength in the future.

Figure 2. (a) Resolution techniques used in recent years, (b) Objective function types used in recent years, (c) Operating model types used in recent years and (d) Consideration of SoC and SoH in storage.

On the other hand, Figure 2b shows the results of the objective function types researchers have used to formulate the mathematical optimization problem in EMS. The red line shows that, in general, SOBJ functions have been considered to have a higher frequency than MOBJ functions. This is an expected result for a technology that focuses on main objectives in early development phases. Nevertheless, a minimum-cost operation is not the only objective of an EMS. In fact, authors have recently considered other objectives to improve MG overall performance, e.g., reduction of polluting gases, maximization of the use of renewable resources, maximization of the useful life of batteries, etc.

Upon the penetration of several DG technologies, electrical vehicles, and controllable loads, the need for a more detailed modeling of system components is a well-known issue in the context of distribution systems. Thus, a proper management of reactive power requirements, minimization of losses, and unsymmetrical operations is required. However, this consideration introduces non-linear equations that increase formulation complexity and computational burden ^[29]. This can explain that, in recent years, the authors have generally considered the use of DC load flow operating models. In fact, the results in Figure 2c show a predominant use of DC load flow approaches with nearly 85% of the references. In spite of the evidence, the authors expect an increase in AC approaches in the future.

Both SoC and SoH are important features to be considered in the operation of the EMS. Figure 2d shows the results on how these attributes are considered in the EMS mathematical optimization problem. In general, the large majority of the papers (nearly 70% on average) have considered the SoC to be part of the mathematical problem. In contrast, only about 15% of the papers integrate the SoH attribute into the optimization problem. No clear trends could be identified over the years for both attributes.

The high penetration of renewable generation into MGs increases multiple power injection variability. Furthermore, load forecasting uncertainty in MGs is higher compared with bulk power systems. This is explained by a high preponderance of individual loads in total MG loads and the integration of electromobility. The factors described above should be considered in EMS optimization approaches ^[30]^[31] to achieve more realistic and cost-effective results. 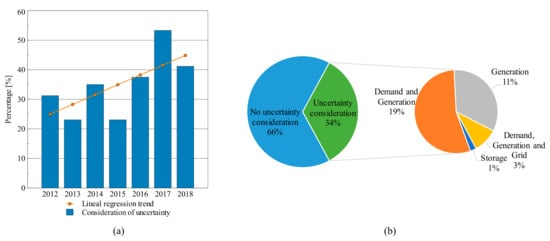Figure 3 summarizes these results. The orange line (linear regression trend) shows that the consideration of uncertainties into the EMS mathematical problem has increased in recent years. Figure 3a shows that in the years 2017 and 2018, uncertainties were considered in approximately 53% and 41% of the papers, respectively. Additionally, Figure 3b shows the distribution of modeled uncertainties such as generation profile, load forecast, grid electricity prices, and storage SoC. Furthermore, Figure 3b shows that the authors have generally considered the uncertainty in generation and load while storage uncertainty seems to be at an early stage but increasing in importance. Electromobility can be a key driver in this direction ^[32].

Figure 3. (a) Uncertainty trend in recent years, (b) Uncertainty consideration distribution in different MG agents.

The results of this section help to identify structural research issues from a comprehensive database of research works from past years. Thus, main resolution techniques, objective functions options, load flow types, storage attributes, and the integration of uncertainties were identified. Nevertheless, apart from the uncertainties (Figure 3), it was not possible to identify trends over the period of analysis (2012–2018). Moreover, a traditional quantitative analysis could not reveal how these research aspects are related. This situation motivated the following cluster analysis.

2.3. Cluster Analysis

The cluster analysis proposed is used in this section to identify additional trends in EMS developments. Only such features holding enough information (see Table 1) are considered for obtaining and analyzing these trends (e.g., detail level of components (A), objective function (B), resolution technique (C), operating model (F), and consideration of uncertainties (H)). More specifically, this identification is performed by using the Kohonen self-organizing maps (SOM) tool. The SOM is a clustering and data visualization technique based on a neural network approach. As with other types of centroid-based clustering, the objective of SOM is to find a group of centroids (reference vectors in SOM terminology) and assign each object in the data group to the centroid that provides the best approximation of that object ^[33].

Table 1. Features and attributes of the distinctive papers selected.

Ref.	A	B	C			D	E	F	G	H	I	J
Ref.	A	B	MP	CI	HM	D	E	F	G	H	I	J
^[34]	STM	SOBJ	MILP			OIN	DSET + OOU	DC	DY	DM + GE		MIN
^[35]	STM	MOBJ			MO + FL + ANN	GFO + OIN	DSET	DC	DY	DM + GE
^[36]	STM	SOBJ	MINLP			GFO + DFO + OIN	OOU	DC	HR
^[37]	STM	SOBJ		LO		OIN	DSET + DSM	AC	DY	GE

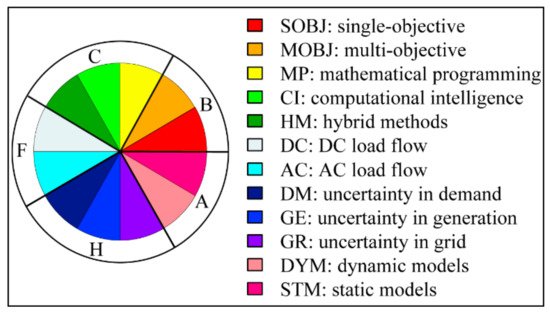
To better visualize these trends, the SOM is integrated into RStudio ^[38]. It associates different colors to each attribute (e.g., red for SOBJ, yellow for MP; etc.) for a general view of the final results. The color code associated to each attribute is shown in Figure 4.

Figure 4. Attributes considered with their respective associated color.

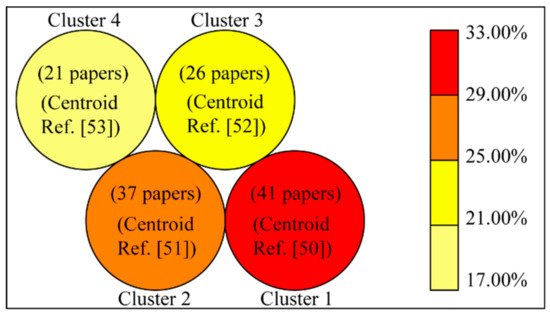
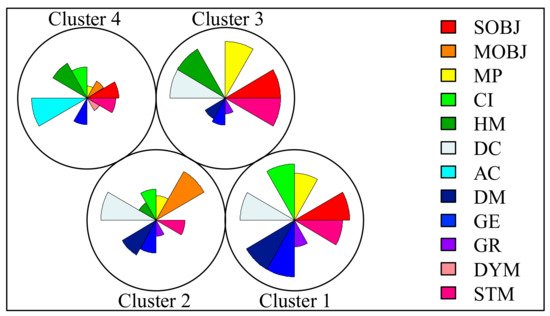
Four distinctive groups are identified with the aid of the clustering technique. Figure 5 shows the number of papers contained by each group. Each of these groups has its respective features depending on the most common attributes present in the papers from a specific group (see Figure 6). The chart consists of a sequence of equiangular spaces, with each area representing one of the attributes. The data length of every pie is proportional to the magnitude of the attribute (weight) for the data point against the maximum magnitude of the variable across all data points. Furthermore, for every cluster there is a paper with the shortest distance to their representing attribute. This distinctive paper is known as the centroid of the cluster to which it belongs (see Figure 5). Table 2 shows the centroids (papers) for each cluster jointly with a detailed classification of their attributes.

Figure 5. Number of papers in each cluster.

Figure 6. Main attributes of each cluster.

The following modeling strategies, accordingly EMS trends, are identified based on this combination of attributes (see Figure 5 and Figure 6):

Cluster 1: Dealing with uncertainties: This cluster comprises 33% of the references; therefore, it is the main research trend. Its distinctive feature is the challenge of modeling the uncertainties present in various MG agents (DM, GE, GR) that will impact the performance of the EMS. This is in line with the general idea that uncertainties are becoming an increasingly important issue in MG developments due to DER integration, more active participation of loads, and electromobility. Basic modeling strategies involve static representation of components (STM) and a DC load flow approach. The optimization model corresponds to a SOBJ function, and it is solved by either MP or CI methods. This is a reflection of alternative solution techniques exploration in research proposals. Surprisingly, HMs are not part of this EMS development trend.

As previously mentioned, the centroid of Cluster 1 corresponds to Reference ^[34] (see Table 1). In this work, a strategy to deal with uncertainties associated with generation and demand is presented. The SOBJ objective function considered is total profit maximization. The optimization problem is formulated by using the MP technique MILP and solved by employing CPLEX. The focus is only on the interchange of active power among power generators, energy storage, energy consumption, and the grid. Thus, DC load flow is considered. Finally, MG components are formulated as STMs (discrete-time formulation). By following step (8) from the proposed procedure, new research-specific challenges in this trend are:

How to solve further problems entailing higher complexities by combining reactive and proactive techniques and considering the uncertainty of renewable resources and load consumption.
Guidelines to a simultaneous consideration of different factors (i.e., costs, environmental impact, social aspects, etc.) through the implementation of multi-objective optimization approaches.

Cluster 2: Multi-objective strategy: This cluster contains approximately 29% of the references. This second leading trend addresses a multi-objective approach. For this purpose, three resolution techniques are used for the resulting optimization problem, with a slight predominance of CI approaches. Uncertainties in the fields of DM and GE have been considered on a general basis. In this case, a DC load flow approach is also the basic network modeling approach. Nonetheless, as mentioned , a predominance of SOBJ approaches in the near future may be expected; a research community with a focus on MOBJ challenges exploring several solution techniques can be clearly identified.

The centroid of Cluster 2 corresponds to Reference ^[35]. The authors propose a MOBJ framework to minimize operational costs and the environmental impact of an MG. The mathematical problem is solved through FL and ANN, CI techniques used jointly with MP. The problem formulation includes optimum battery scheduling while considering the uncertainties of MG DERs and forecasted parameters. The objective functions are only subjected to active power constraints; therefore, a DC load flow is considered.

Research-specific challenges are:

How a combination of CI and traditional techniques can achieve a clear and important minimization of operation costs, greenhouse gases emissions, and other technical and economic MG-related issues.
How to achieve a highly accurate forecasting of renewable energy sources by using CI techniques, in order to comply with an efficient MG energy management.

Cluster 3: Traditional paradigm: This third cluster contains approximately 21% of the references. By conceiving a traditional approach for EMS developments, the following options might be selected: SOBJ instead of MOBJ, a deterministic approach instead of focusing on uncertainty modeling, well proven MP approaches, a static representation of components (STM) instead of a DYM approach and finally a focus on active power simulation (DC) vs. an AC paradigm. This is exactly what can be observed in this modeling trend. This type of development can be expected to be very useful for improving current commercial EMS solutions that usually follow a more traditional modeling strategy. The only unexpected feature is a substantial use of HM for the solution techniques. This issue may indicate that most research proposals and innovations in this research group address the migration of traditional MP techniques. This makes use of the advantages of combining CI solutions that constitute HM strategies. In Figure 2a, a positive evolution of this strategy is identified.

The centroid of Cluster 3 is the paper in Reference ^[36]. In this work, a traditional SOBJ function is used to minimize the total cost of energy. The authors assumed that the voltage level is the same at all MG busses—a DC load flow operating model. MG components are formulated as STMs in a time-discrete formulation resulting in a number of algebraic constraints. Proposed energy management is based on local energy market and allows scheduling MG generation with minimum information shared by the generating units. For EMS optimization, the authors propose a novel algorithm based on a MINLP approach for an MG in islanding mode considering different scenarios. The optimization problem is solved in a GAMS/CONOPT environment.

The following specific challenges were identified:

How to enable the owners of the distributed generation units to establish their own strategies to participate in MG generation with minimum information shared between distributed generators. Additionally, comply with consumer’s requirements with a minimum energy cost.
How to use demand response programs either to avoid or to decrease penalty costs and the amount of unserved power, as well as to improve demand side management.

Cluster 4: The P-Q challenge: This last cluster contains approximately 17% of the references. As mentioned in the previous section, proper management of reactive power requirements, voltage profile, ohmic losses minimization, and unsymmetrical operations are well-known issues in MG developments. Nevertheless, Figure 2c does not identify a clear trend in this field. On the contrary, the cluster analysis was able to extract a trend in this field, where AC modeling is in the core of the solution approaches, together with a predominance of CI-based solution techniques. Additionally, a more deterministic focus in modeling approaches is identified, with the exception of uncertainties in generation (GE). This is the only trend that incorporates STM and some DYM approaches. Additionally, the use of either SOBJ or MOBJ proposals has been identified in this field.

The centroid of Cluster 4 corresponds to Reference ^[37]. In this study, an online EMS for real-time operation of MGs is presented that considers the power flow and system operational constraints. The SOBJ formulation is to minimize the long-term operational cost, while delivering reliable and high-quality power to customers. Online energy management is modeled as a stochastic optimal power flow (AC load flow model) capable of capturing uncertainties in generation (GE). The EMS problem is solved by the Lyapunov optimization approach (CI).

Finally, the following research-specific challenges are:

How to properly consider the underlying power distribution network and its associated power flow and system operational constraints in order to achieve control decisions that do not transgress real-world constraints.
How to develop an intelligent algorithm on the customer side to generate demand requests that allow the EMS to make more accurate operating decisions in the MG.

These papers’ analyses on cluster centroids validate the rationality of cluster descriptions and their main attributes.

2.3. Key Lessons Learned, Key Challenges, and Future Research Directions

The key challenges and the way to cope with them are identified based on the analysis of each trend, the results of previous reviews, and the previous experience of the authors.

Uncertainties in renewables is a topic with an increasing interest to researchers (see Figure 3a) but that is only partially integrated by the research community with a third of research results. It can be envisaged that uncertainties in renewables, demand, and grids will become a common modeling aspect in EMS proposals in the near future. Decentralized solutions will increasingly integrate local renewable sources required by small productive processes (e.g., agriculture, farming, tourism, etc.). Consequently, more complex customer/prosumer behaviors are expected. The modeling of this type of load involves new uncertainties and the need of new simulation strategies that exceeds the traditional ZIP approach (load model that considers constant impedance “Z”, constant current “I”, and constant power “P” components) or a time series analysis.

Some obstacles for the researchers to cope with additional modeling challenges that occur on a simultaneous basis have been identified, e.g., multiple objective functions, full AC network representations, and the application of hybrid solution methods. Each of these combinations constitute new challenges in this research area. In fact, researchers have recently considered introducing more than one objective into the objective functions to enhance overall MG performance (e.g., minimization of operational cost, reduction of polluting gases, maximization of the service life of batteries, etc.). An emerging topic in this field is the integration of dynamic socio-environmental preferences from the local community. The work on the relative weights of the different objective functions is limited, and new consensus strategies resulting from community participation are being developed. Socio-environmental preferences may also be linked to present and future economic costs, which are not only related to the cost of electricity. The integration of all the foregoing is optimal for developing an EMS that considers all real-world constraints while satisfying consumer requirements at the same time. This increase in complexity will impact not only the computational burden of the resulting optimization problems but also the convexity properties of mathematical models, the availability and quality of input data, communication network requirements (bandwidth), cost reduction needs, among others. Based on the specific MG features (size, type and number of technologies, environmental conditions, etc.) a balance and trade-off analysis should be conducted by the researchers in order to develop adequate and practical proposals. Internet of Things (IoT) may play a key role in this area for both the access to a wide range of information sources and types and the cost-effective data acquisition approach. In fact, an important benefit of IoT to MGs is the ability to control non-critical loads (demand side management), which is the ability to run the MG at the lowest possible cost whilst providing the highest possible reliability to provide power to critical loads and improve its flexibility. Moreover, IoT allows the application of DSM in a context of diverse commercial solutions of appliances, a common issue related to MG globally. In this context, more accurate and computationally efficient dynamic models for critical MG components are needed. The centralized approach needs a representation of the critical stability aspects related to operational decisions. The transition between the operation modes is a clear example in the case of isolated operations. The feasibility and impact of each transition should be considered as part of the EMS optimization strategy. Nowadays, this aspect is only considered for specific MG configurations (i.e., failure of the master unit and replacement of a specific predefined back-up unit). This constitutes a barrier for a massive integration of these solutions in everchanging local conditions.

On the other hand, storage systems are one key component for EMS operation. Thus, both SoC and SoH should be fully considered in the EMS mathematical optimization problem. However, according to the findings from this work, SoH is still not considered on a frequent basis. Consequently, research efforts should focus on developing valid, general, and suitable SoH models to be included in the EMS mathematical problem. Moreover, to consider multiple storage systems in a single, MG.; equivalent storage system approaches or clustering should be considered.

The results have shown that most of these papers hold a high consideration of DC load flow. However, reactive power is also an important part of MG and should be considered in energy management to achieve a reliable and secure system. However, this consideration introduces non-linear equations that increase formulation complexity and computational burden. Therefore, research efforts should focus on developing low complexity and computationally efficient AC load flow models.

To solve the EMS mathematical optimization problem, MP, CI, and HM have been used. CI approaches have advantages in convergence speed and large-scale problem solving compared to MP methods. However, CI techniques may fall into local optima as MG complexity increases. HM approaches that combine the benefits of the above methods have attracted researchers’ attention. Thus, it could be a great opportunity to focus on developing new HM approaches.

The results of this research trend analysis show that there is no evidence of a research cluster where all EMS development challenges were dealt with on a simultaneous basis. In fact, research proposals in every cluster are mainly focused on the improvement of specific areas, while making some simplifications in others. Thus, these proposals can be addressed with the mathematical and computational resources currently available. A clear understanding of each of the four trends identified can be considered a good starting point and guidance for future research contributions. In spite of current proposals imposing some simplifications, they have been accepted for the deployment of EMSs around the world.

Finally, innovative DSM and storage applications and concepts may play a key role to overcome the current and future challenges faced in the design and solutions of MGs. Thus, more cost-effective, reliable, social, and environmentally compatible solutions are feasible. These opportunities, i.e., key enablers for massive MG integration, have not been properly addressed in the literature.

References

Torbaghan, S.S.; Blaauwbroek, N.; Kuiken, D.; Gibescu, M.; Hajighasemi, M.; Nguyen, P.; Smit, G.J.; Roggenkamp, M.; Hurink, J. A market-based framework for demand side flexibility scheduling and dispatching. Sustain. Energy Grids Netw. 2018, 14, 47–61.
Olatomiwa, L.; Mekhilef, S.; Ismail, M.S.; Moghavvemi, M. Energy management strategies in hybrid renewable energy systems: A review. Renew. Sustain. Energy Rev. 2016, 62, 821–835.
Lasseter, B. Microgrids [distributed power generation]. In Proceedings of the 2001 IEEE Power Engineering Society Winter Meeting Conference Proceedings (Cat. No.01CH37194), Columbus, OH, USA, 28 January–1 February 2001; Volume 1, pp. 146–149.
Lasseter, R.H. MicroGrids. In Proceedings of the 2002 IEEE Power Engineering Society Winter Meeting Conference Proceedings (Cat. No.02CH37309), New York, NY, USA, 27–31 January 2002; Volume 1, pp. 305–308.
An, L.N.; Quoc-Tuan, T. Optimal energy management for grid connected microgrid by using dynamic programming method. In Proceedings of the 2015 IEEE Power Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5.
Shen, J.; Jiang, C.; Liu, Y.; Wang, X. A Microgrid Energy Management System and Risk Management Under an Electricity Market Environment. IEEE Access 2016, 4, 2349–2356.
Huang, K.; Wang, X.; Wang, L. Optimal energy management of grid-connected photovoltaic micro-grid. In Proceedings of the 2015 IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems, Shenyang, China, 8–12 June 2015; pp. 234–239.
Ma, L.; Liu, N.; Zhang, J.; Tushar, W.; Yuen, C. Energy Management for Joint Operation of CHP and PV Prosumers Inside a Grid-Connected Microgrid: A Game Theoretic Approach. IEEE Trans. Ind. Inform. 2016, 12, 1930–1942.
Arcos-Aviles, D.; Pascual, J.; Guinjoan, F.; Marroyo, L.; Sanchis, P.; Marietta, M.P. Low complexity energy management strategy for grid profile smoothing of a residential grid-connected microgrid using generation and demand forecasting. Appl. Energy 2017, 205, 69–84.
Mohan, V.; Singh, J.G.; Ongsakul, W.; Madhu, M.N.; Reshma Suresh, M.P. Economic and network feasible online power management for renewable energy integrated smart microgrid. Sustain. Energy Grids Netw. 2016, 7, 13–24.
Gabbar, H.A.; Zidan, A. Optimal scheduling of interconnected micro energy grids with multiple fuel options. Sustain. Energy Grids Netw. 2016, 7, 80–89.
Marino, C.; Quddus, M.A.; Marufuzzaman, M.; Cowan, M.; Bednar, A.E. A chance-constrained two-stage stochastic programming model for reliable microgrid operations under power demand uncertainty. Sustain. Energy Grids Netw. 2018, 13, 66–77.
Ismail, M.S.; Moghavvemi, M.; Mahlia, T.M.I. Techno-economic analysis of an optimized photovoltaic and diesel generator hybrid power system for remote houses in a tropical climate. Energy Convers. Manag. 2013, 69, 163–173.
Dahmane, M.; Bosche, J.; El-Hajjaji, A.; Dafarivar, M. Renewable energy management algorithm for stand-alone system. In Proceedings of the 2013 International Conference on Renewable Energy Research and Applications, Madrid, Spain, 20–23 October 2013; pp. 621–626.
Dash, V.; Bajpai, P. Power management control strategy for a stand-alone solar photovoltaic-fuel cell–battery hybrid system. Sustain. Energy Technol. Assess. 2015, 9, 68–80.
Nasri, S.; Sami, B.S.; Cherif, A. Power management strategy for hybrid autonomous power system using hydrogen storage. Int. J. Hydrog. Energy 2016, 41, 857–865.
Chalise, S.; Sternhagen, J.; Hansen, T.M.; Tonkoski, R. Energy management of remote microgrids considering battery lifetime. Electr. J. 2016, 29, 1–10.
Amrollahi, M.H.; Bathaee, S.M.T. Techno-economic optimization of hybrid photovoltaic/wind generation together with energy storage system in a stand-alone micro-grid subjected to demand response. Appl. Energy 2017, 202, 66–77.
Manbachi, M.; Ordonez, M. AMI-based Energy Management for Islanded AC/DC Microgrids Utilizing Energy Conservation and Optimization. IEEE Trans. Smart Grid 2018, 1.
Katiraei, F.; Iravani, R.; Hatziargyriou, N.; Dimeas, A. Microgrids management. IEEE Power Energy Mag. 2008, 6, 54–65.
Eskandari, M.; Li, L.; Moradi, M.H. Improving power sharing in islanded networked microgrids using fuzzy-based consensus control. Sustain. Energy Grids Netw. 2018, 16, 259–269.
Aluisio, B.; Dicorato, M.; Forte, G.; Trovato, M. An optimization procedure for Microgrid day-ahead operation in the presence of CHP facilities. Sustain. Energy Grids Netw. 2017, 11, 34–45.
Javadi, M.; Marzband, M.; Akorede, M.; Godina, R.; Saad, A.; Pouresmaeil, E. A Centralized Smart Decision-Making Hierarchical Interactive Architecture for Multiple Home Microgrids in Retail Electricity Market. Energies 2018, 11, 3144.
Hatziargyriou, N. Microgrid: Architectures and Control, 1st ed.; Wiley-IEEE Press: New Jersey, NY, USA, 2014.
Pourbabak, H.; Chen, T.; Su, W. 1-Centralized, Decentralized, and Distributed Control for Energy Internet; Su, W., Huang, A.Q.B.T.-T.E.I., Eds.; Woodhead Publishing: Cambridge, UK, 2019; pp. 3–19.
Rafique, S.F.; Jianhua, Z. Energy management system, generation and demand predictors: A review. IET Gener. Transm. Distrib. 2018, 12, 519–530.
Senjyu, T.; Kuninaka, R.; Urasaki, N.; Fujita, H.; Funabashi, T. Power system stabilization based on robust centralized and decentralized controllers. In Proceedings of the 2005 International Power Engineering Conference, Singapore, 29 November–2 December 2005; Volume 2, pp. 905–910.
Almasalma, H.; Engels, J.; Deconinck, G. Peer-to-Peer Control of Microgrids 2017. Available online: https://arxiv.org/pdf/1711.04070.pdf (accessed on 3 January 2020).
Olivares, D.E.; Cañizares, C.A.; Kazerani, M. A Centralized Energy Management System for Isolated Microgrids. IEEE Trans. Smart Grid 2014, 5, 1864–1875.
Xiang, Y.; Liu, J.; Liu, Y. Robust Energy Management of Microgrid With Uncertain Renewable Generation and Load. IEEE Trans. Smart Grid 2016, 7, 1034–1043.
Theo, W.L.; Lim, J.S.; Ho, W.S.; Hashim, H.; Lee, C.T. Review of distributed generation (DG) system planning and optimisation techniques: Comparison of numerical and mathematical modelling methods. Renew. Sustain. Energy Rev. 2017, 67, 531–573.
Ravichandran, A.; Sirouspour, S.; Malysz, P.; Emadi, A. A Chance-Constraints-Based Control Strategy for Microgrids With Energy Storage and Integrated Electric Vehicles. IEEE Trans. Smart Grid 2018, 9, 346–359.
Tan, P.-N.; Steinbach, M.; Kumar, V. Introduction to Data Mining, 1st ed.; Pearson: Boston, MA, USA, 2005; Volume 1.
Silvente, J.; Kopanos, G.M.; Pistikopoulos, E.N.; Espuña, A. A rolling horizon optimization framework for the simultaneous energy supply and demand planning in microgrids. Appl. Energy 2015, 155, 485–501.
Chaouachi, A.; Kamel, R.M.; Andoulsi, R.; Nagasaka, K. Multiobjective Intelligent Energy Management for a Microgrid. IEEE Trans. Ind. Electron. 2013, 60, 1688–1699.
Marzband, M.; Sumper, A.; Domínguez-García, J.L.; Gumara-Ferret, R. Experimental validation of a real time energy management system for microgrids in islanded mode using a local day-ahead electricity market and MINLP. Energy Convers. Manag. 2013, 76, 314–322.
Shi, W.; Li, N.; Chu, C.; Gadh, R. Real-Time Energy Management in Microgrids. IEEE Trans. Smart Grid 2017, 8, 228–238.
RStudio. RStudio: Integrated Development for R. Available online: http://www.rstudio.com/ (accessed on 3 January 2020).

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Energy & Fuels

Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Danny Espín-Sarzosa

Oscar Núñez-Mata

View Times: 824

Update Date: 26 Sep 2021

Table of Contents

Video Upload Options

Confirm