Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
ADNAN ALI
 + 4250 word(s) 4250 2021-09-14 10:52:44 |
2 format correct
Conner Chen
 Meta information modification 4250 2021-09-24 10:51:43 |

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Ali, A. Structure of Oxide Perovskite. Encyclopedia. Available online: https://encyclopedia.pub/entry/14440 (accessed on 23 November 2024).
Ali A. Structure of Oxide Perovskite. Encyclopedia. Available at: https://encyclopedia.pub/entry/14440. Accessed November 23, 2024.
Ali, Adnan. "Structure of Oxide Perovskite" Encyclopedia, https://encyclopedia.pub/entry/14440 (accessed November 23, 2024).
Ali, A. (2021, September 23). Structure of Oxide Perovskite. In Encyclopedia. https://encyclopedia.pub/entry/14440
Ali, Adnan. "Structure of Oxide Perovskite." Encyclopedia. Web. 23 September, 2021.
Structure of Oxide Perovskite
Edit
This entry is adapted from the peer-reviewed paper 10.3390/catal11091057

Materials crystalizing in the perovskite crystal structure are common crystals that are currently employed for multiples applications, including transistors, solar cells, light-emitting devices, memories, catalysts, and superconductors.
One of the biggest players within the perovskite structures is the family of oxide perovskites. This is a prominent family with the general formula of ABO3, where A commonly designates an alkaline or rare earth metal cation, occupying the 12-fold coordinated cuboctahedral cages of the oxygen sub-lattice, and B stands for a transition-metal cation (e.g., Fe, Ni, Mn, Co, Cu, or Ti) coordinated with six oxygen atoms in an octahedral coordination. In fact, in the perovskite structure, distortions frequently occur due to the deviation from ideal values of ionic size ratios between the different A, B, and O sites of the crystal. In addition, A or B cations may have distinctive sizes and valences that could result into oxygen non-stoichiometry, involving both oxygen excess and/or oxygen deficiency.

oxide perovskite metal–halide perovskite plasmonics photovoltaics Photocatalysis

1. Structure of Oxide Perovskite

In the ideal cubic unit cell of a perovskite compound, type “A” atoms are located at the cube corner, at the positions (0, 0, 0), type “B” atoms at the center position (1/2, 1/2, 1/2) and oxygen atoms located at the face positions (1/2, 1/2, 0). Figure 1a shows a ball and stick representation of cubic unit cell where A ions occupy the edges, B ions the center and O ions occupy the faces.

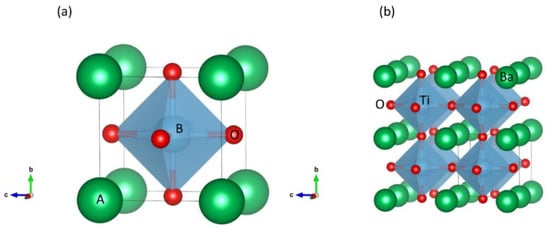
Catalysts 11 01057 g002 550

Figure 1. Stick and ball and stick schematic of the (a) ideal cubic perovskite structure unit cell, and (b) a supercell for BaTiO3 structure.

The relative ion size rules that govern the stability of the ideal cubic structure such as the “Goldsmith tolerance factor” are quite rigid, such that minor buckling and octahedral distortion shall reduce the distorted versions of the symmetry in which the coordination numbers of A, B or both cations are reduced. BO6 octahedral tilting decreases the coordination of an undersized A cation from 12 to as low as 8. In fact, it helps in attaining a stable bond pattern by removing a small B cation from the center of this octahedron. The resulting electric dipole is the key factor governing the ferroelectricity as shown by perovskites, for example BaTiO3 (Figure 2b) that distort in this fashion. The most predominant non-cubic variants are the orthorhombic and tetragonal phases. Double perovskites can form upon the incorporation of two distinct B-site cations, forming complex perovskite structures and leading to the formation of ordered and disordered crystal structures.

Complex or mixed oxides are cation groups that contain two or more distinct cations. There are several types of crystal structures. In certain distinctive cases, oxides of a single cation are often known as mixed oxides in different oxidation states.

Perovskite is another significant mixed oxide structure, and many similar oxide structures are known perovskites. The structure of the ilmenite is the same as that of perovskite, i.e., ABO3, where in this structure, A and B are cations occupying octahedral site of somewhere around the same size; however, the anion packing arrangement is hexagonal and compact in the ilmenite, whereas in the perovskite, the anion and A cation form a close, compact, and a cubic packing structure. Ilmenite has similar stoichiometry to perovskite, but the chemical formula is different. The key difference between ilmenite and perovskite is that ilmenite is an iron-based titanium oxide, i.e., FeTiO3 mineral, whereas perovskite is a calcium-based titanium oxide, i.e., CaTiO3 mineral. Moreover, another significant difference between ilmenite and perovskite is that ilmenite is weakly magnetic, whereas perovskite is a non-magnetic material.

In oxide compounds, perovskite oxides have vast families and many perovskite-related structures have been already identified. Large-sized 12-coordinated A-site cations and smaller 6-coordinated B-site cations are standard structures. Wide ranges of oxides and halides, as well as sulfides and perovskites, have a perovskite composition. Because of Therefore, magnesium and iron silicates such as (Mg,Fe)SiO− or CaSiO3 are generally assumed as the geosphere’s primary constituent. Scientists have discovered combinations of different charged cations in sites A and B, such as 1 + 5, 2 + 4 and 3 + 3, relating to various types of perovskite compounds. Although more complex combinations such as Pb(B′1/2B″1/2) have been found. It is important to keep in mind that B′ is always a group containing Sc or Fe, and B″ is always a group containing Nb or Ta. Numerous ABO3 compounds often crystallize in polymorphic structures that exhibit a slight distortion from the perovskite structure symmetry.

For perovskite, a cubic lattice is the ideal structure and is shown in Figure 2. Numerous oxides have twisted a little with lower symmetries, despite the fact that few compounds have this ideal cubic structure (e.g., hexagonal or orthorhombic). In addition, although the ideal cubic structure of certain compounds may be intact, most oxides feature variants with a lower degree of symmetry. Table 1 lists many examples of perovskite oxides, where the perovskite oxides have mostly grown as rhombohedral lattices.

Table 1. Typical example of perovskite oxides, where the perovskite oxides have mostly grown as rhombohedral lattices.

Compound Lattice Parameters (Å)
a b c
A. Cubic Structure
KTaO3 3.989    
NaTaO3 3:929    
NaNbO3 3:949    
BaMnO3 4:040    
BaZrO3 4:193    
SrTiO3 3:904    
KMnF3 4:189    
KFeF3 4:121    
B. Tetragonal Structure
BiAlO3 7:61   7:94
PbSnO3 7:86   8:13
BaTiO3 3:994   4:038
PdTiO3 3:899   4:153
TlMnCl3 5:02   5:04
C. LaAlO3 type
LaAlO3 5:357 α=60∘06'  
LaNiO3 5:461 α=60∘05'  
BiFeO3 5:632 α=60∘06'  
KNbO3 4:016 α=60∘06'  
D. GdFeO3 type
GdFeO3 5:346 5:616 7:668
YFeO3 5:283 5:592 7:603
NdGaO3 5:426 5:502 7:706
CaTiO3 5:381 5:443 7:645

A significant characteristic of many compounds is that they often have a wide degree of oxygen or cation deficiencies. The perovskite oxides share the large lattice energy, but due to the large cation and/or oxygen deficiencies, a substantial number of these compounds are nonetheless labeled as perovskite oxides. Ferromagnetism and ferroelectricity are associated forms of distortions within the perovskite structure.

These ABO3 oxides are strictly termed as ionic crystals for a better understanding of the deviations from the ideal cubic structure. The radii of the A, B, and O2− ions in the ideal structure have the following relationship:

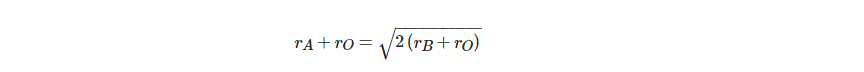
Consequently, by using the Goldsmith tolerance factor t, ideal cubic structure deviancy can be determined in perovskite oxides:

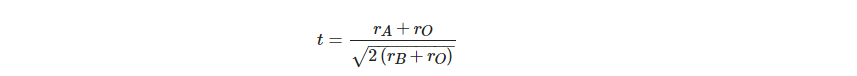
The t value in perovskite-type compounds is usually between 0.80 and 1.10, i.e., an ideal cubic structure. t values reflect the different polymorphs that exist for perovskite structures. In Figure 2, elements are shown which can be inserted into the perovskite structure are shown. Almost all elements, including dopants, will inhabit the perovskite structure at either A or B positions in the lattice, with the exception of noble gases. In terms of stability and crystal structure, for the A and B cations, ionic radii ratio of is the most significant factor for determining the perovskite structure stability. Structure is not only reliant on the size of the A and B atoms, but also on their chemical composition. For instance, AMnO3 forms a perovskite structure when the A cation is La or Ce–Dy, and forms a hexagonal structure when A = Ho ‒ Lu or Y if A = La or Ce − Dy with 5- and 7- coordination of Mn and A, respectively [1].

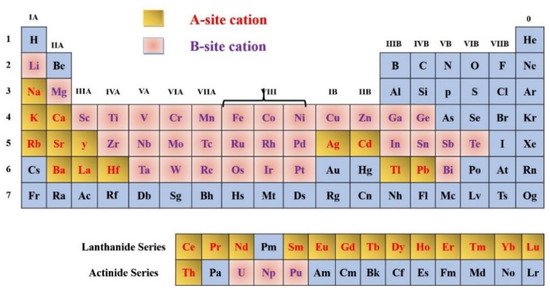
Catalysts 11 01057 g003a 550Catalysts 11 01057 g003b 550

Figure 2. (Upper panel) In the perovskite structure, the B-site cation can be taken by chemical elements. (Lower panel) Representation of the oxide family (left), halides (right), single (top), and double (below) perovskites, and other analogs.

At this site, the primary emphasis should be on the B atom’s nature, where the covalent bond nature causes a coordination number of 6, which is rather low. The structure of BaGeO3 is an example of this kind. Although the ideal ionic size combination of BaGeO3 results in a t value near to 1, which implies the perovskite structure, BaGeO3 instead crystallizes in the silicate-related structure. The coordination number of Ge is four, which can be attributed to this. On the other hand, new Ge-based perovskite oxides have been identified from the developments in high-pressure technology [2]. By increasing the pressure, the Ge coordination number increases, and this higher coordination number is favorable for the formation of the perovskite structure, e.g., CaGeO3. Oxynitrides are another perovskite compounds group, i.e., LaWO3−xNx, LaTaO2N, etc. As a result, the ionic size which is dependent on the tolerance factor value t, is an important index for perovskite structure stability. However, the coordinating number contribution of the constituent elements must also be considered.

Next, superstructure formations in perovskites are discussed. Progressive substitution of the B-site cation by a dopant contributes to a significant difference in the ionic radii, and this can be conducive to the formation of the superstructures. Ba2CaWO6, also known as Ba2(CaW)O6, is a clear example of this. Analogously, when M is Fe, Co, Ni, Zn, or Ca, there is a random distribution of M and Ta ions in the octahedral positions in the compounds with the general formula Ba3MTa2O9, whereas Ba3SrTa2O9 forms a hexagonal lattice superstructure. On A sites, the cation vacancy ordering, as seen in MNb3O9 (M = La, Ce, Pr, Nb) and MTa3O9 (M = La, Ce, Pr, Nd, Sm, Gd, Dy, Ho, Y, Er), is another interesting form of superstructure observed in perovskites. Often known as the Brownmillalite (A2B2O5) and K2NiF4 structures, the perovskite polymorphs contain these two. The low-oxygen-deficiency type of perovskite, where oxygen vacancies are ordered, is known as Brownmillalite (A2B2O5).

In an ordered arrangement, the unit cell comprises BO6 and BO4. The A-site cation coordination number is reduced to eight due to the oxygen deficiency. For an ideal perovskite, the cubic lattice parameter (ap) is associated with the lattice parameter of Brownmillalite structure:

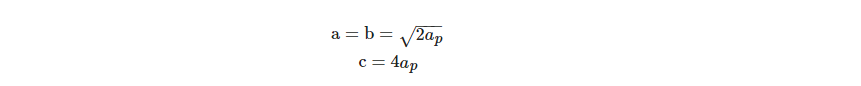
Due to the large number of oxygen defects, Cu-based oxides and Ni-based oxides both develop oxygen-deficient structures. For exhibiting superconducting properties, K2NiF4 structures are well known and are found to be combined with ordered B-sites and oxygen defects.

Two units, namely the KNiF3 perovskite unit and the KF rock salt unit, are linked in series along the c axis to form K2NiF4 structures. K2NiF4 is entrenched in the c-axis direction, and it has strong two-dimensional properties. There are several structures known as Ruddelsden–Popper compounds with the general formula (ABO3)nAO (see Figure 3), such as Sr3Ti2O7 (n = 2) and Sr4Ti3O10 (n = 3), based on the intergrowth of different numbers of KNiF3 and KF units [3]. The isostructural Sr2TiO4 or Ca2MnO4 can be contrasted with SrTiO3 or CaMnO3, which crystallize in perovskite structures. It is also possible to shape the perovskite and rock salt units with two separate A cations: an example of this is LaO.nSrFeO3. An even more significantly modified version of K2NiF4 is where the two separate anions exclusively occupy the two building blocks, i.e., SrFeO3.SrF or KNbO3.KF. For any scenario, it is obvious that these structures are complex compounds. As a result, these compounds are supposed to possess various crystal properties and characteristics [4][5][6].

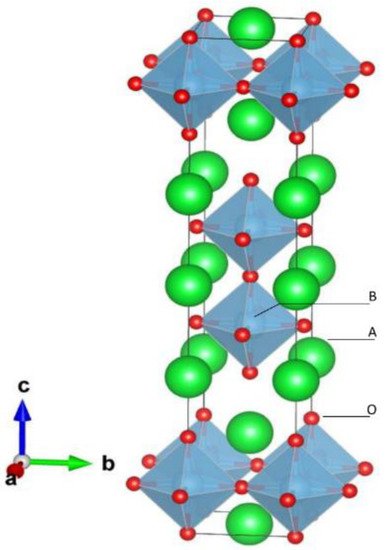
Catalysts 11 01057 g004 550

Figure 3. Another perovskite-related structure is the Ruddelsden Popper structure.

The layered perovskite family contains several polar and ferroelectric materials in contrast to bulk ABO3 perovskites. The (100)-oriented 2D perovskites are by far the most abundant class, and have been explored for a wide variety of cation templates. The geometrically planar inorganic–organic interface of the (100)-oriented layers not only allows the incorporation of a plethora of “spacer” cations between the 2D perovskites, but it also allows for the template “build-up” of the perovskite itself, which self-assembles in a layer-by-layer fashion between the spacers. These modular multilayered structures were first discovered in the oxide perovskites, where they were used to expand extended homologous series [3][7]. Following the oxide perovskite nomenclature, the (100)-oriented oxide perovskites can be further categorized as the Ruddlesden Popper (RP) phases [8][9], the Dion Jacobson (DJ) phases [8][9], and the Aurivillius phases [10][11], as shown in Figure 4, [12] where their general formulae can be written as A′2An−1BnO3n+1, A′An−1BnO3n+1 and (Bi2O2)(An−1BnO3n+1), respectively.

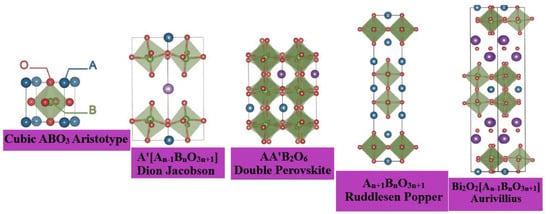
Catalysts 11 01057 g005 550

Figure 4. Layered perovskites—derived from the cubic ABO3 aristotype—are discussed in this perspective. In the Dion Jacobson phases, A′ is usually an alkali cation, but can also be a transition metal–halide complex, e.g., (MnCl)+. In the A-site ordered double perovskites, A′ is chemically different from A. The perovskite blocks are interleaved between [Bi2O2]2+ layers in the Aurivillius phases. Adapted from Refs. [10][11] with permission from the European Society for Photobiology, the European Photochemistry Association, and The Royal Society of Chemistry.

In the case of halide perovskites, most of these structure types have been realized, with the exception of the Aurivillius phases. It is entirely possible, however, that such layers can be formed using less reactive rock-salt-type layers, such as (Ba2F2)2+. As in the case of oxide perovskites, as well as in the case of halide perovskites, the nature of the spacer cation is important. Already, from the expression of the chemical formula, it is evident that the charge of the spacer cation defines the structural types of 2D perovskites. Nevertheless, both RP and DJ classes exist for the halide family, having the general formula of A′2An−1BnX3n+1 and A′An−1BnX3n+1 (A′ = interlayer “spacer” cation).

2. Formability versus Thermodynamic Stability

Recently, Talapatra et al. [13] studied the relationship between two key properties governing the stability of single and double perovskites. The formability stands for the practical ability to synthesize a compound, whereas the thermodynamic stability stands for the thermodynamic preference to form a given structure or polymorph among several other possible crystal structures. The data set contains information from the literature which have been reported from experimental research as well as from DFT calculations. It consisted of 1505 simple oxide perovskites ABO3 and 3469 double-oxide perovskites A2B′BO6, AA′B2O6 and AA′BB′O6, sampling a limited chemical space within the periodic table. They subsequently built machine learning classification models to screen and identify novel stable oxide perovskites. One of the most important finding is that they succeeded to make a clear difference between the perovskite’s formability and the thermodynamic stability and to relate these two stability measures to the elemental properties of constituent chemical elements.

The formability of perovskites relies on geometrical consideration based on the ionic radii of the perovskites as well details in the sections above. However, this formability metric, although popular, does not inform us on whether the perovskite structure is the most favorable compared to other possible crystal structure, here is where the importance of thermodynamic stability arises. Under certain conditions, including temperature, pressure or variation in chemical potentials, some other crystal structures of polymorphs might be more stable than the perovskite one, even if they are favorably formable. The distance from the convex hull, also called ΔEh, might be a better thermodynamic stability measurement. Authors [13] have used the threshold of ΔEh ≤ 50 meV as the limit that defines the cubic thermodynamic stability of the oxide perovskite, which is a value that is highly accepted by the community [14][15]. Using a random forest classification algorithm, Talapatra et al. [13] determined the most elemental features governing both stability metric and generated a very good accuracy predictive model for both stability metrics. Figure 5a shows an interesting finding within a plot of the energy above the hull as a function of the geometrical tolerance factor for the groups of materials that fulfill both the formability and stability criteria. One might notice that below the ΔEh = 50 meV, dashed line lies a high population of perovskite material (66%), whereas the prevalence on non-perovskites is rather rare. Nevertheless, a non-negligible fraction of the compounds was excluded from the thermodynamic stability because of their high energy above the hull. Taking ΔEh < 400 meV as a threshold appears to give more reliable classifications of the compounds, as also demonstrated from the histogram of incidence (frequency) of perovskites and non-perovskites within ΔEh bins of 50 meV each. The histogram indicates that up to ΔEh = 400 meV compounds crystalizing in the perovskite structure are dominant, as shown in Figure 5b.

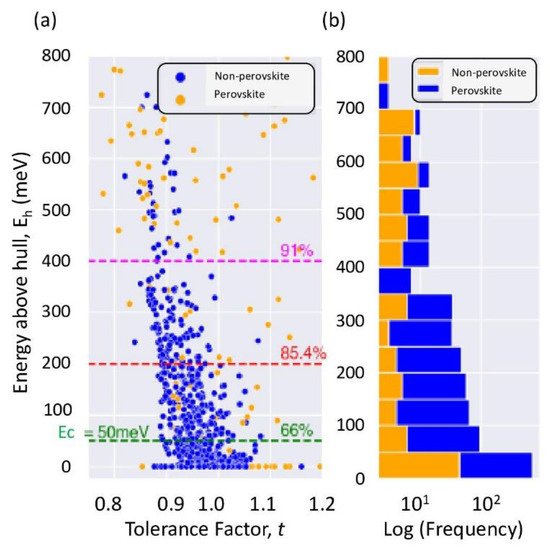
Catalysts 11 01057 g006 550

Figure 5. (a,b) Energy above hull (ΔEh) in meV as a function of tolerance factor (t) for candidate materials identified as stable and formable. Reproduced with permission from Ref. [13].

Hence, the cubic thermodynamic threshold of ΔEh  ≤ 50 meV might not be a reliable threshold for the metastability of oxide perovskite because it does account for stability enhancements due to octahedral tilts and octahedral deformation and elongations. It is concluded that the thermodynamic cubic stability must be selected carefully and should be tuned properly to include lower symmetry phases as well. This study and previous studies constitute very interesting advances in the prediction of novel oxide perovskites for targeted applications while taking into account their stability and formability prior to recommending their experimental synthesis in the laboratory.

3. Typical Properties of Perovskite Oxides

Perovskite oxides have a diverse plethora of properties because of their different compositions and structures. In BaTiO3-based oxides, and in Ba2YCu3O7, perovskite oxides exhibit ferroelectricity and superconductivity, respectively. Several perovskite oxides also exhibit substantially greater electric conductivity, ionic conductivity, and mixed ionic conductivity than many metals. For use in solid oxide fuel cells (SOFC), perovskite oxides have been preferred, with components based on differences in electrical conduction [16]. Table 2 lists the properties of several common perovskite oxides. Perovskite oxides take on several feature properties, such as ferroelectricity, magnetism, superconductivity, and catalysis.

Table 2. Typical perovskite oxide properties.

Typical Properties Typical Compound
Ferromagnetism PdTiO3, BaTiO3
Electrical conductivity ReO3, SrFeO3, LaCoO3, LaNiO3, LaCrO3
Superconductivity La0.9Sr0.1CuO3, YBa2Cu3O7, HgBa2Ca2Cu2O8
Piezoelectricity (Bi, Na)TiO3, Pb (Zr, Ti)O3
Magnetism LaMnO3, LaFeO3, La2NiMnO6
Ion conductivity BaZrO3, SrZrO3, BaCeO3, La(Ca)AlO3, CaTiO3, La(Sr)Ga(Mg)O3
Electrode materials La0.8Ca0.2MnO3, La0.6Sr0.4CoO3
Catalytic properties LaCoO3, BaCuO3, LaMnO3

3.1. Dielectric Properties

Ferroelectricity, piezoelectricity, electrostricity, and pyroelectricity, which are important electroceramic characteristics, are special properties of dielectric materials. BaTiO3, PdZrO3, and their doped compounds are all well known for their ferroelectricity. It has been investigated in depth that there is a close correlation between the ferroelectric activity of BaTiO3 and its crystal structure. BaTiO3 can be present in three distinct phases: monoclinic, tetragonal, and cubic. The transition between the phases occurs with a rise in temperature. As a matter of fact, above 303 K, cubic BaTiO3 is obtained, which is non-ferroelectric in nature. Crystal structure anisotropy may explain BaTiO3’s high dielectric constant.

3.2. Electrical Conductivity and Superconductivity

The superconductivity of perovskite oxides is the most famous characteristic among the other features. In La–Ba–Cu–O perovskite oxide, superconductivity was found and introduced for the first time by Bednorz and Müller in 1984 [17]. After their report, much attention was drawn towards high-temperature superconductors, particularly Cu-based oxides, which were given much attention after their report. Other than Cu-based oxides, data have been reported on numerous superconducting oxides with different A-site cations. On the B-site, Cu presence is crucial for superconductance, however. YBa2Cu3O7 system [17] and Bi2Sr2Ca2Cu3O10 system [18] superconductors were reported in 1987 and 1988, respectively. The critical temperature of the superconducting transition (Tc) in the HgBa2Ca2Cu3O8+δ system has been further increased to 130–155 K [17]. All superconducting oxides at high temperatures are cuprites; therefore, superconductivity is specifically correlated with the layers of copper oxide, as well as the Tc (critical superconductivity temperature), and the values are summarized in Table 3:

Table 3. Superconductivity correlated with the number of Cu–O layers.

Number of Layers Tc (K)
1 30
2 90
3 110
4 120

A further rise in Cu–O layer numbers is predicted to contribute to higher Tc values. Five or more copper oxides layers have not been effective until now due to the low chemical stability. YBa2Cu3O7 is amongst the most significant high-Tc superconductor systems, and extensive studies have been already carried out on its crystal structure. In addition, the nonstoichiometric oxygen content is a key factor in high Tc. If the d value is less than 0.5, YBa2Cu3O7 crystalizes in a superconductive orthorhombic structure, whereas for d > 0.5, it is tetragonal structure, which is non-superconducting.

In addition to the superconductivity, there are numerous perovskite oxides with a high electronic conductivity, even close to that of metals such as Cu. LaCoO3 and LaFeO3 are the most common examples of perovskite oxides, whereas LaMnO3 is now widely used in SOFCs as a cathode. Superior hole conductivity as high as σ = 100 S/cm is exhibited by these perovskite oxides, which is attributed to the of excess oxygen [19][20]. Doping at the aliovalent cation site also leads to considerably improve the electrical conductivity, because the charge compensation creates an increased number of mobile charge carriers.

3.3. Catalytic Activity

Perovskite oxides have been investigated in depth as catalysts for different reactions, due to the diversity of components and their high chemical stability. Two types of research-trends are indicated on this front. The first one is related to develop catalysts for oxidation as a substitute to the precious metals catalysts, or oxygen-activated catalysts. The second one is to consider the perovskite as an active site platform. The stable nature of perovskite enables compounds to be prepared with an exceptional element of valences or with an enhanced degree of oxygen deficiency. It has been reported that perovskite oxides provide a high catalytic activity because there are a lot of oxygen vacancies, and it also depends -although partly- on the high surface activity to reduce oxygen or to activate it. From the examination of different catalytic reactions, environmental catalysis has gained a special attention (e.g., catalysts for the exhaust gas cleaning of automobiles). Initially, perovskite oxides, comprising Fe, Cu, Mn or Co, were known to increase activity at higher temperatures than that obtained from a direct NO decomposition [21][22][23]. The process related to 2NO = N2 + O2, where a direct NO decomposition takes place, is an ideal reaction in the catalysis. Easy separation of oxygen at the surface as a reaction product has a vital role because perovskite oxides are active due to oxygen deficiency at high temperatures. Doping is noted to be highly successful in enhancing the NO decomposition operations. It has been identified that the perovskite Ba(La)Mn(Mg)O3, in a rich environment of oxygen, can obtain a fairly high NO decomposition rate (up to 5%) [22][23][24].

Perovskite oxides are also used as catalysts for automobiles for the self-regeneration of precious metals in a usage ambience without auxiliary treatment [25][26]. To date, for the removal of NO, CO and non-combusted hydrocarbons, three-way catalysts (TWC) and Pd–Rh–Pt catalysts have been used widely. The fine particle catalyst with a high volume-to-surface ratio must lower the needed quantity of precious metals. Even then, they are not stable under operational circumstances and can sinter easily, and the catalyst is therefore deactivated. The redox properties of perovskite oxides were suggested in order to preserve a high degree of dispersion, i.e., palladium is oxidized under oxidation conditions and stays as LaFe0.57Co0.38Pd0.05O3 where palladium nanoparticles (1–3 nm) are deposited under reduced conditions. Such oxidation and reduction of the catalyst lead to partial Pd substitution and deposition from the perovskite base, thereby retaining a high degree of Pd dispersion. This was considered to be significantly successful in enhancing long-term Pd stability while removing NOx, CO and hydrocarbons from the gas exhausted. By displaying the catalyst in oxidation and reduction environments, high-dispersion status Pd can be restored. Therefore, this catalyst is often termed as an intelligent catalyst. Such character is attributed to the perovskite crystal structure stability. In the lattice, the redox couples of another cation naturally accommodate for the charge. Photocatalysts for water splitting are another important application of perovskite oxides. The use of ultraviolet light among catalysts for water splitting into H2 and O2 is observed to have an increased activity of perovskite oxide based on Ta and Na.

3.4. Photocatalytic Activity

It is possible to use photo-excited electrons and holes to split H2O into H2 and O2, and this process gains more attention in solar energy conversion into hydrogen. Several inorganic catalysts for water splitting have been investigated as water photocatalysts, especially Pt/TiO2 as a well-known photocatalytic inorganic semiconductor. In the photocatalytic water-splitting reaction, the Ta-based oxide is normally active. The Ta-based perovskite oxide, ATaO3 (A = alkaline cation), specifically displays high water-splitting activity [27]. The A cation strongly affects the activity because the crystal structure is linked to the oxide’s electronic configuration. The Ta–O–Ta bond angles are 143° (LiTaO3), 163° (NaTaO3), and 180° (KTaO3). The bonding angle close to 180° means that excited energy migration easily occurs in the crystal and results in a smaller band gap. Hence, LiTaO3 < NaTaO3 < KTaO3 is the delocalization order of excited energy and vice versa for these band gaps, as shown in Figure 6. Table 4 presents the photocatalytic water-splitting activities of pure water into H2 and O2 on alkaline tantalite photocatalysts with and without NiO cocatalysts. When NiO cocatalysts were loaded, NaTaO3 photocatalysts demonstrated the highest photocatalytic activity. In this case, excessive amounts of Na in the starting material were necessary to demonstrate high activity. The photocatalyst NaTaO3’s conduction band level was higher than the NiO level (−0.96 eV), as shown in Figure 6 [27]. In addition, in the NaTaO3 crystal, the excited energy was delocalized. Therefore, the photogenerated electrons in the NaTaO3 photocatalyst’s conductive band were capable of passing to the NiO cocatalyst’s conduction band of an active site for H2 generation, leading to an increase in the separation of the charge. Hence, even without special pretreatment, NiO loads were successful for the NaTaO3 photocatalyst.

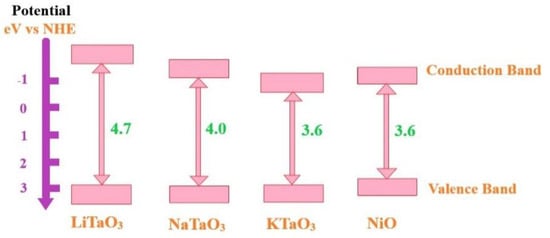
Catalysts 11 01057 g007 550

Figure 6. Band diagram of a hydrogen electrode-based alkali tantalates ATaO3 (A = W Li, Na, and K) band structures with perovskite-type structures. Adapted from Ref. [27].

Table 4. Appropriate perovskite oxide materials for use in SOFCs.

Component Typical Materials
Interconnector La(Ca)CrO3
Anode SrTiO3, La1‒xSrxCr1‒yMyO3 (M = Mn, Fe, Co, Ni),
Electrolyte La(Sr)Ga(Mg)O3(O2−), SrZrO3(H+), Ba2In2O5(O2−), BaCeO3(H+), BaZrO3(H+),
Cathode La(Sr)Fe(Co)O3, La(Sr)CoO3, La(Sr)MnO3, Sm0.5Sr0.5CoO3

References

  1. Geller, S.; Jeffries, J.B.; Curlander, P.J. The crystal structure of a new high-temperature modification of YGaO3. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1975, 31, 2770–2774.
  2. Liebermann, R.C.; Jones, L.E.; Ringwood, A. Elasticity of aluminate, titanate, stannate and germanate compounds with the perovskite structure. Phys. Earth Planet. Inter. 1977, 14, 165–178.
  3. Schaak, R.E.; Mallouk, T. Perovskites by Design: A Toolbox of Solid-State Reactions. Chem. Mater. 2002, 14, 1455–1471.
  4. Chern, M.Y.; Vennos, D.; Disalvo, F. Synthesis, structure, and properties of anti-perovskite nitrides Ca3MN, M=P, As, Sb, Bi, Ge, Sn, and Pb. J. Solid State Chem. 1992, 96, 415–425.
  5. Zhao, Y.; Daemen, L.L. Superionic Conductivity in Lithium-Rich Anti-Perovskites. J. Am. Chem. Soc. 2012, 134, 15042–15047.
  6. Stølen, S.; Bakken, E.; Mohn, C.E. Oxygen-deficient perovskites: Linking structure, energetics and ion transport. Phys. Chem. Chem. Phys. 2005, 8, 429–447.
  7. Aleksandrov, K.S. Structural phase transitions in layered perovskitelike crystals. Crystallogr. Rep. 1995, 40, 251–272.
  8. Ruddlesden, S.N.; Popper, P. The compound Sr3Ti2O7and its structure. Acta Crystallogr. 1958, 11, 54–55.
  9. Ruddlesden, S.N.; Popper, P. New compounds of the K2NIF4type. Acta Crystallogr. 1957, 10, 538–539.
  10. Aurivillius, B. Mixed bismuth oxides with layer lattices. 2. Structure of Bi4Ti3O12. Ark. Kemi. 1950, 1, 499–512.
  11. Aurivillius, B. Mixed bismuth oxides with layer lattices. 1. The structure type of CaNb2Bi2O9. J. Ark. Kemi. 1950, 1, 463–480.
  12. Benedek, N.A.; Rondinelli, J.M.; Djani, H.; Ghosez, P.; Lightfoot, P. Understanding ferroelectricity in layered perovskites: New ideas and insights from theory and experiments. Dalton Trans. 2015, 44, 10543–10558.
  13. Talapatra, A.; Uberuaga, B.P.; Stanek, C.R.; Pilania, G. A Machine Learning Approach for the Prediction of Formability and Thermodynamic Stability of Single and Double Perovskite Oxides. Chem. Mater. 2021, 33, 845–858.
  14. He, Z.; Gu, J.H.; Sha, W.E.I.; Chen, R.S. Efficient volumetric method of moments for modeling plasmonic thin-film solar cells with periodic structures. Opt. Express 2018, 26, 25037–25046.
  15. Ali, A.; Park, H.; Mall, R.; Aïssa, B.; Sanvito, S.; Bensmail, H.; Belaidi, A.; El-Mellouhi, F. Machine Learning Accelerated Recovery of the Cubic Structure in Mixed-Cation Perovskite Thin Films. Chem. Mater. 2020, 32, 2998–3006.
  16. Mitchell, R. Perovskite Modern and Ancient; Almaz Press: Thunder Bay, ON, USA, 2002.
  17. Bednorz, J.G. Possible highTc superconductivity in the Ba−La−Cu−O system. Z. Für Phys. B Condens. Matter. 1986, 64, 189–193.
  18. Hor, P.H.; Meng, R.L.; Wang, Y.Q.; Gao, L.; Huang, Z.J.; Bechtold, J.; Forster, K.; Chu, C.W. Superconductivity above 90 K in the square-planar compound system ABa/sub 2/Cu/sub 3/O/sub 6+//sub x/with A= Y, La, Nd, Sm, Eu, Gd, Ho, Er and Lu. Phys. Rev. Lett. 1987, 58, 1891–1894.
  19. Gao, L.; Xue, Y.Y.; Chen, F.; Xiong, Q.; Meng, R.L.; Ramirez, D.; Chu, C.W.; Eggert, J.H.; Mao, H.K. Superconductivity up to 164 K in HgBa2Cam−1CumO2m+2+δ (m = 1, 2, and 3) under quasihydrostatic pressures. Phys. Rev. B 1994, 50, 4260–4263.
  20. Mizusaki, J.; Yoshihiro, M.; Yamauchi, S.; Fueki, K. Nonstoichiometry and defect structure of the perovskite-type oxides La1−xSrxFeO3−°. J. Solid State Chem. 1985, 58, 257–266.
  21. Mizusaki, J.; Yasuda, I.; Shimoyama, J.; Yamauchi, S.; Fueki, K. Electrical Conductivity, Defect Equilibrium and Oxygen Vacancy Diffusion Coefficient of La1−xCaxAlO3−δ Single Crystals. J. Electrochem. Soc. 1993, 140, 467–471.
  22. Whang, S.-J.; Lee, S.; Chi, D.-Z.; Yang, W.-F.; Cho, B.-J.; Liew, Y.F.; Kwong, D.-L. B-doping of vapour–liquid–solid grown Au-catalysed and Al-catalysed Si nanowires: Effects of B2H6 gas during Si nanowire growth and B-doping by a post-synthesis in situ plasma. Nanotechnology 2017, 18, 275302.
  23. Teraoka, Y.; Harada, T.; Kagawa, S. Reaction mechanism of direct decomposition of nitric oxide over Co- and Mn-based perovskite-type oxides. J. Chem. Soc. Faraday Trans. 1998, 94, 1887–1891.
  24. Yasuda, H.; Nitadori, T.; Mizuno, N.; Misono, M. Catalytic Decomposition of Nitrogen Monoxide over Valency-Controlled La2CuO4-Based Mixed Oxides. Bull. Chem. Soc. Jpn. 1993, 66, 3492–3502.
  25. Iwakuni, H.; Shinmyou, Y.; Yano, H.; Matsumoto, H.; Ishihara, T. Direct decomposition of NO into N2 and O2 on BaMnO3-based perovskite oxides. Appl. Catal. B Environ. 2007, 74, 299–306.
  26. Nishihata, Y.; Mizuki, J.I.; Akao, T.; Tanaka, H.; Uenishi, M.; Kimura, M.; Okamoto, T.; Hamada, N. Self-regeneration of a Pd-perovskite catalyst for automotive emissions control. Nature 2002, 418, 164–167.
  27. Maeda, K. Photocatalytic water splitting using semiconductor particles: History and recent developments. J. Photochem. Photobiol. C Photochem. Rev. 2011, 12, 237–268.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Crystallography
Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
ADNAN ALI
View Times: 4.3K
Revisions: 2 times (View History)
Update Date: 24 Sep 2021
Table of Contents
    1000/1000
    Hot Most Recent
    ScholarVision Creations
    Feedback