
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Oluwaseun Adedeji | + 5435 word(s) | 5435 | 2021-09-10 12:04:54 | | | |
| 2 | Lindsay Dong | Meta information modification | 5435 | 2021-09-14 04:55:13 | | |
Video Upload Options
Slurry pipe transport has directed the efforts of researchers for decades, not only for the practical impact of this problem, but also for the challenges in understanding and modelling the complex phenomena involved. The increase in computer power and the diffusion of multipurpose codes based on Computational Fluid Dynamics (CFD) have opened up the opportunity to gather information on slurry pipe flows at the local level, in contrast with the traditional approaches of simplified theoretical modelling which are mainly based on a macroscopic description of the flow.
1. Introduction
1.1. Engineering Aspects and Physical Features of Slurry Pipe Transport
1.2. Modeling of Slurry Pipe Flows
Predictive models are essential design tools for slurry transport systems. In this perspective, the prediction of the pipe characteristic curve is one of the key tasks of slurry flow modelling, and another major task is to predict the deposition-limit velocity, Vdl, which is the value of flow velocity below which solid deposit is observed. A more detailed prediction of slurry flow includes information on the internal structure of the flow in the form of distributions of local velocity and concentration (e.g., [11]) which helps to understand the friction and to predict other phenomena, such as the erosive wear of a pipe wall.
There are several sorts of models available for predictions of the slurry flow quantities. It has been shown that different slurries can form quite different flow types with different flow patterns and it must be emphasized that the different slurry flows exhibit rather different flow behaviors [12][13]. An identification of the flow type is essential for the successful modelling of slurry flows and prediction of their behavior in a pump-pipeline transport system. The available models rely on different approaches, which have different levels of complexity and refinement, so that, in principle, simpler approaches are easier to use but provide less refined outputs.
1.3. The Potential of Computational Fluid Dynamics
The complexity of solid–liquid flow as is the flow of settling slurry demands that the flow behavior is best analyzed on a local level by monitoring distributions of flow quantities throughout the flow domain. This requirement focuses attention on Computational Fluid Dynamics. Traditionally, CFD simulations for engineering purposes have been restricted to simpler one-phase flows primarily due to limitations in computer power and the capability of CFD codes. However, current advancements in this field have enabled to increase the amount of research work on the numerical simulation of pipe flows of slurry exponentially in few years, opening the way to the use of this approach for the engineering applications.
2. CFD Modelling Approaches
2.1. Eulerian–Lagrangian Modelling


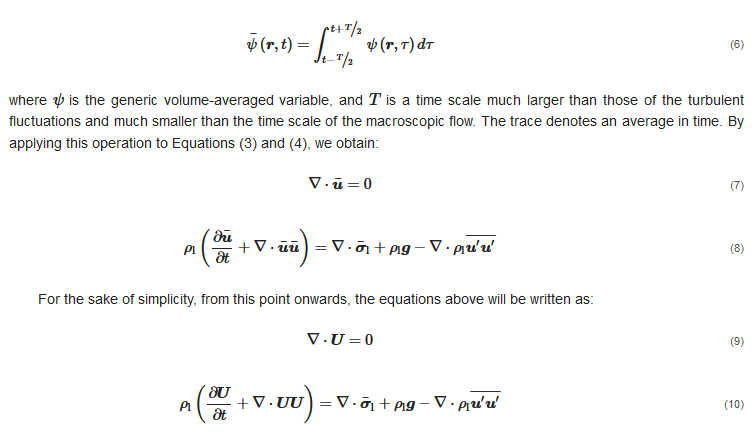



2.1.1. One-Way Coupled Slurry Flows
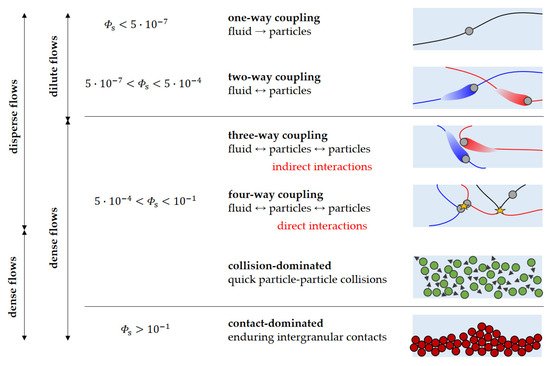
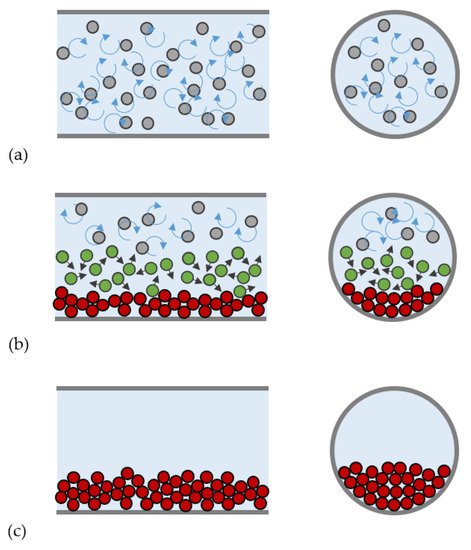
2.1.2. Two and Four-Way Coupled Slurry Flows

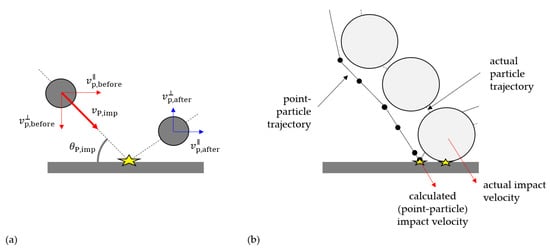
2.1.3. Boundary Conditions
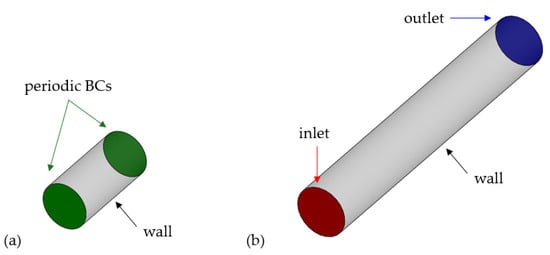

2.2. Eulerian–Eulerian Modelling (Two-Fluid Modelling)
2.2.1. Fundamental Conservation Equations
In the Eulerian–Eulerian approach, both phases are interpreted as interpenetrating continua and they are modelled in the Eulerian, cell-based framework. This is achieved by solving for the fundamental mass and momentum conservation equations for two media, namely, the carrier liquid and a fictitious fluid representing the fluid dynamic behavior of the ensemble of solid particles, called “solid phase”. The instantaneous equations of the two-fluid model can be derived in different ways, and they typically read as follows:
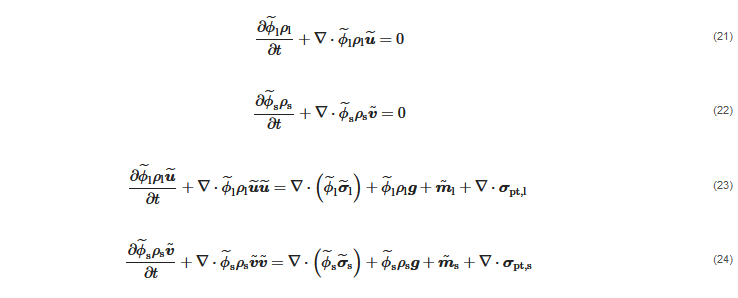
2.2.2. Constitutive Equations

where λl is called the second viscosity coefficient. Note that, in principle, the volume-averaged velocity field u˜ is not divergence-free for incompressible carriers. Therefore, the last term in Equation (26) is not identically zero, even if it is usually neglected in Euler–Euler models, obtaining a formally similar relation as in the classical Eulerian–Lagrangian approach (Equation (5)). However, the situation becomes more complicated for the solid phase. Solving Equation (25), in fact, requires facing the non-trivial challenge of how to characterize from a physical point of view (first) and how to evaluate (afterwards) the pressure and deviatoric stress tensor of the solid phase. Generally, a solid-phase analogous of Equation (26) is employed, as follows:


In the KTGF, the six variables listed above are algebraic functions of Θs as well as other particle-related parameters, such as the restitution coefficient of particle–particle collisions, the solid volume fraction at maximum packing, and the angle of internal friction. The granular temperature, in turn, is obtained from the solution of its own transport equation. However, other two-fluid models for slurry pipe flow simulation do not rely on the KTGF but use empirical constitutive equations for μs and p˜s. As far as μs is concerned, a possible approach was mentioned in [39], which consists in estimating μs from the viscosity of the mixture μm.
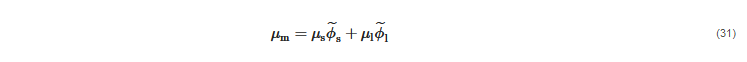
2.2.3. Interfacial Momentum Transfer
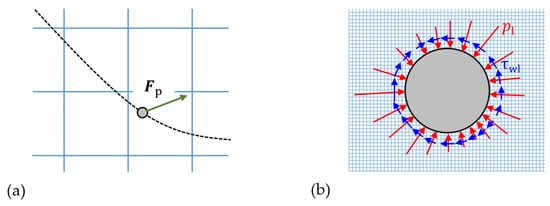
The terms m˜k (k = l,s), called interfacial momentum transfer terms, account for the exchange of forces between the two phases through their interface. Following Enwald et al. [39], these parameters can be expressed in terms of the interfacially-averaged pressure and deviatoric stress tensor, p˜i and τ˜i, as follows:


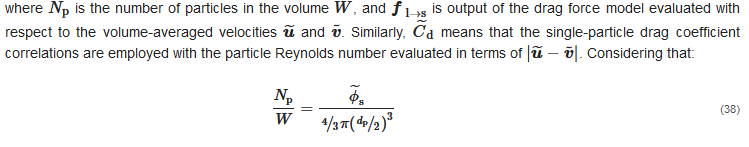
it is possible to rewrite Equation (37) as

2.2.4. Modelling of Turbulent Flows
The equations illustrated so far are intended to be the instantaneous ones, valid for both laminar and turbulent flows. However, to keep the computational burden within acceptable limits and meet the engineering needs, the modelling of turbulent flows is generally carried out by solving only for the mean flow or the largest scales of turbulence. However, the Eulerian–Eulerian analogous of the RANS approach for single-phase flow is definitely complex to derive, as well as to characterize and justify from a physical point of view. In this regard, the double-average approach provides a strong mathematical ground for the derivation of the two-fluid models for turbulent flows. Essentially, the idea is to start from the instantaneous, volume-averaged equations and apply a second averaging operator, obtaining double-averaged equations whose unknowns are the double-average of the fluid dynamic variables (pressure, velocity, volume fraction, etc.). For the second averaging operator, two main options have been documented in the literature. The former consists of applying the same time average operator in Equation (6) to all volume-averaged variables, that is,
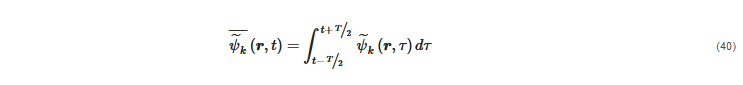
The latter option is to use the time average for all variables except for the velocity, to which the Favre operator is applied
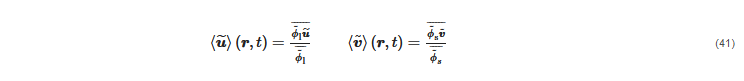
As illustrated by Burns et al. [26], the fundamental conservation equations assume different forms according to the second averaging operator applied. This is immediately evident in the mass conservation equations. After time-averaging, the mass conservation equations become:

Comparing the two sets of equations above indicates that, when time-averaging of the volume-averaged mass conservation equations is performed, two additional terms come up, associated with the double correlations between the fluctuating velocity vector and the fluctuating volume fraction. These terms require modelling, which is typically achieved through the gradient diffusion approximation, initially proposed by Spalding [27] based on an analogy between the turbulent dispersion of solid particles and the turbulent diffusion of a passive scalar:
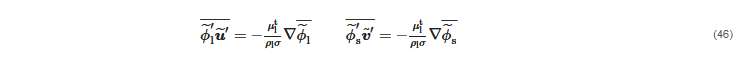
Whatever the second averaging operator is, double averaging of the momentum conservation equations produces several terms depending on double and triple correlations between fluctuations, which need to be modelled by additional closures. Elghobashi and Abou-Arab [28] reported the equations obtained by time-averaging the volume-averaged equations, and the momentum ones consist of about 15 terms. Most of these terms are simply ignored in commonly used two-fluid models, either because they are small or difficult to estimate. One might think that ignoring some terms might deviate the numerical solution from the physical one. However, it should be borne in mind that closure correlations are never exact, but they rely on approximations and empiricism: therefore, there is no guarantee that adding more closures results in higher accuracy, unless there is no doubt that such closures are applicable to the specific case study under investigation.
Given that, the double correlations associated with the convection terms are usually taken into account in slurry flow simulations. In the case of time-averaging of all variables, they are as follows:

whilst, if the volume-average velocity is Favre-averaged, the form of the double-averaged convection terms is:


As in single-phase flows, the last terms of Equations (51) and (52) do not appear explicitly in the momentum equation of the liquid, as they are usually combined with the pressure gradient one (see Section 2.1). In such eddy viscosity based models, μtl is obtained from two-phase analogous of the turbulence models for the single-phase case. A formulation of the two-phase k-ε turbulence model consistent with the time- and volume-averaged operators was derived by Elghobashi and Abou-Arab [58], in which the two equations for the turbulent kinetic energy and the turbulent dissipation rate consist of 38 and 67 terms, respectively. However, much simpler formulations are used in engineering computations. For instance, the two-phase k-ε turbulence model by Spalding [56] has been frequently used to simulate turbulent slurry flows in pipes, and it reads as follows:

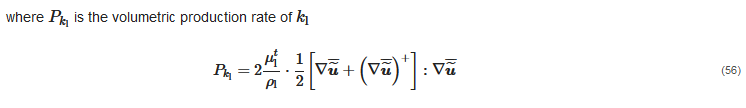
Mandø et al. [29] identified the main criticism of turbulence modulation models in the fact that, according to their derivation, they can predict only either turbulence attenuation or turbulence enhancement, as typical of particle-laden flows with fine and coarse particles, respectively. In order to overcome such limitations, these authors proposed a comprehensive model which can predict both effects at the same time. Such model, employed for simulating gas–solid flows using the Eulerian–Lagrangian approach, which was later generalized and applied to the Eulerian–Eulerian modelling of slurry flows in vertical pipes by Messa and Malavasi [30]. However, a key issue is that all available correlations were developed for dilute flows in the two-way coupling regime, for which the solid content is much lower compared to the high concentrations encountered in hydro-transport applications. The effect of turbulence modulation on the behavior of dense slurry flows, and its modelling, is an open problem. Indeed, in some papers the same expressions of the source term derived for dilute flows have been applied to dense liquid–solid flows in pipes, using the KTGF and empirical formulas for evaluating the correlations between the fluctuating velocities (e.g., [31]); however, no discussion was provided around the validity of such approach, nor it was assessed the actual impact of these terms on the CFD solution.

According to Burns et al. [26], a reasonable first approximation is to treat Dls as constant during the averaging process. Under this assumption, time-averaging of Equation (57) yields:
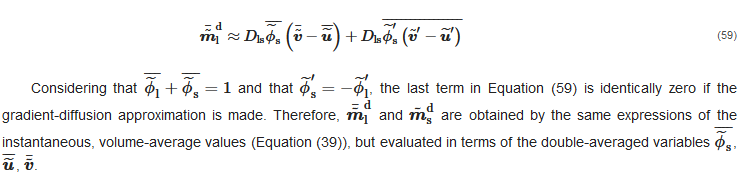
Conversely, if expressed in terms of the Favre-averaged velocities, Equation (59) becomes:

On the grounds of what was stated before, when introducing the gradient-diffusion approximation, the last term disappears, whilst the first two can be arranged, yielding:

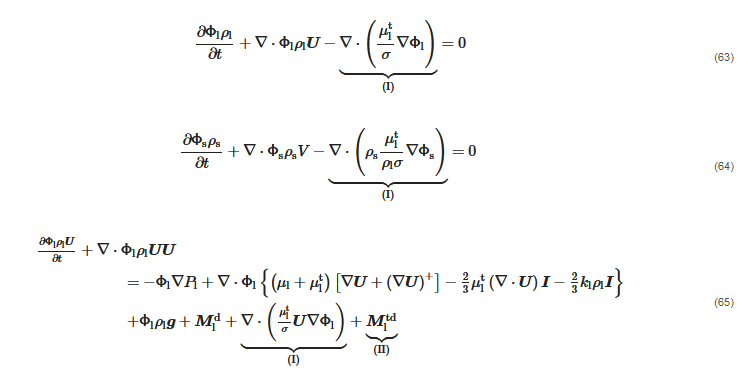

where the phase diffusion terms (I) and the turbulent dispersion force (II) are mutually exclusive of each other.
2.2.5. Boundary Conditions
2.2.6. Multi-Fluid Modelling
2.3. Mixture Modelling
2.3.1. Fundamental Conservation Equations
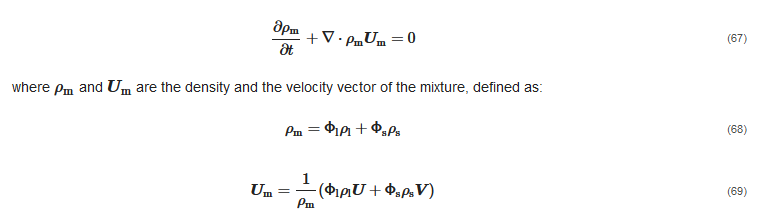
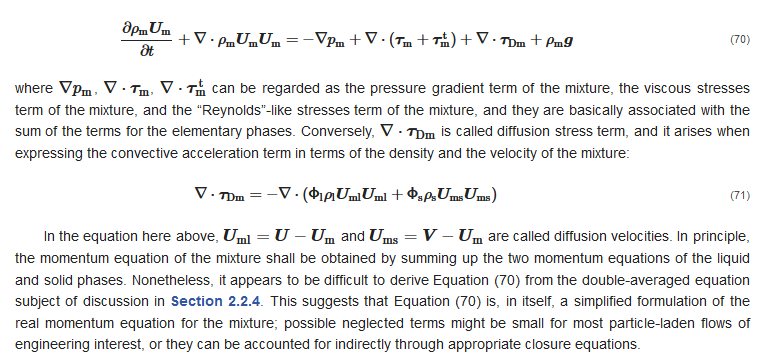

2.3.2. Closure Equations

In the general formulation of Manninen et al. [34], the relative velocity is obtained by combining the momentum equation for the solid phase (Equation (66)) and the momentum equation of the mixture (Equation (70)), applying several simplifying assumptions. The final, implicit expression for the relative velocity reads as follows:



2.3.3. Boundary Conditions
To the best of our knowledge, in all studies concerning the application of the mixture model to slurry pipe flows, the combination of inlet and outlet boundaries was employed (Figure 7b). At the inlet, the distributions of the solid volume fraction and of the velocity of the mixture are imposed, in addition to those of the turbulent parameters, such as km and εm. At the outlet, the pressure of the mixture is specified and held constant, and the normal gradient of all other variables are zero. At the solid walls, the same conditions of single-phase simulations are applied to the mixture. That is, a no-slip condition, which corresponds to zero advection flux from all surface cells; mixture-based wall functions to evaluate the mixture wall shear stress; different types of constraints for the turbulent parameters.
References
- Derammelaere, R.H.; Shou, G. Altamina’s Copper and Zinc Concentrate pipeline incorporates advanced technologies. In Proceedings of the 15th International Conference on Hydrotransport, Banff, AB, Canada, 3–5 June 2002.
- Paterson, A.J.C. Pipeline transport of high density slurries: A historical review of past mistakes, lessons learned and current technologies. Min. Technol. 2012, 121, 37–45.
- van den Berg, C.H. IHC Merwede Handbook for Centrifugal Pumps and Slurry Transportation; MTI Holland: Kinderdijk, The Netherlands, 2013.
- van Wijk, J.M.; Talmon, A.M.; van Rhee, C. Stability of vertical hydraulic transport processes for deep ocean mining: An experimental study. Ocean Eng. 2016, 125, 203–213.
- Thomas, A.D.; Cowper, N.T. The design of slurry pipelines—Historical aspects. In Proceedings of the 20th International Conference on Hydrotransport, Melbourne, Australia, 3–5 May 2017.
- Matoušek, V. Pressure drops and flow patterns in sand-mixture pipes. Exp. Therm. Fluid Sci. 2002, 26, 693–702.
- Talmon, A.M. Analytical model for pipe wall friction of pseudo-homogenous sand slurries. Part. Sci. Technol. 2013, 31, 264–270.
- Spelay, R.; Gillies, R.G.; Hashemi, S.A. Kinematic friction of concentrated suspensions of neutrally buoyant coarse particles. In Proceedings of the 20th International Conference on Hydrotransport, Melbourne, Australia, 3–5 May 2017.
- Wilson, K.C. Deposition-limit nomograms for particles of various densities in pipeline flow. In Proceedings of the 6th International Conference on Hydraulic Transport of Solids in Pipes, Canterbury, UK, 26–28 September 1979.
- Sanders, R.S.; Sun, R.; Gillies, R.G.; McKibbem, M.J.; Litzenberger, C.; Shook, C.A. Deposition velocities for particles of intermediate size in turbulent flow. In Proceedings of the 16th International Conference on Hydrotransport, Santiago, Chile, 26–28 April 2004.
- Gillies, R.G.; Shook, C.A. Concentration distributions of sand slurries in horizontal pipe flow. Part. Sci. Technol. 1994, 12, 45–69.
- Wilson, K.C.; Addie, G.R.; Sellgren, A.; Clift, R. Slurry Transport Using Centrifugal Pumps, 3rd ed.; Springer: New York, NY, USA, 2006.
- Shook, C.A.; Gillies, R.G.; Sanders, R.S.; Spelay, R.B. Saskatchewan Research Council Course Notes; SRC Publications: Saskatoon, SK, Canada, 2013.
- Menter, F. Two equation eddy-viscosity turbulence modeling for engineering applications. AIAA J. 1994, 32, 1598–1605.
- Launder, B.E.; Spalding, D.B. Mathematical Models of Turbulence; Academic Press: London, UK, 1972.
- Prosperetti, A.; Tryggvason, G. Computational Methods for Multiphase Flow; Cambridge University Press: New York, NY, USA, 2007.
- Hager, A. CFD-DEM on Multiple Scales. An Extensive Investigation of Particle-Fluid Interactions. Ph.D. Thesis, Johannes Kepler University Linz, Linz, Austria, 2014.
- Rettinger, C.; Godenschwager, C.; Eibl, S.; Preclik, T.; Schruff, T.; Frings, R. Fully resolved simulations of dune formation in riverbeds. In High Performance Computing; Kunkel, J.M., Yokota, R., Balaji, P., Keyes, D., Eds.; Springer: New York, NY, USA, 2017; pp. 3–21.
- Peng, Z.; Doroodchi, E.; Luo, C.; Moghtaderi, B. Influence of void fraction calculation on fidelity of CFD-DEM simulation of gas-solid bubbling fluidized beds. AIChE J. 2014, 60, 2000–2018.
- Zheng, E.; Rudman, M.; Kuang, S.; Chryss, A. Turbulent coarse-particle suspension flow: Measurement and modelling. Powder Technol. 2020, 373, 647–659.
- Loth, E. Particle, Drops, and Bubbles. Fluid Dynamics and Numerical Methods; Draft for Cambridge University Press: 2010. Available online: www.academia.edu (accessed on 31 August 2021).
- Elghobashi, S. On predicting particle-laden turbulent flows. Appl. Sci. Res. 1994, 52, 309–329.
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Meth. Appl. Mech. Eng. 1974, 3, 269–289.
- Huber, N.; Sommerfeld, M. Modelling and numerical calculation of dilute-phase pneumatic conveying in pipe systems. Powder Technol. 1998, 99, 90–101.
- Breuer, M.; Alletto, M.; Langfeldt, F. Sandgrain roughness model for rough walls within Eulerian-Lagrangian predictions of turbulent flows. Int. J. Multiph. Flow 2012, 43, 157–175.
- Burns, A.D.; Frank, T.; Hamill, I.; Shi, J.M. The Favre averaged drag model for turbulent dispersion in Eulerian multi-phase flows. In Proceedings of the 5th International Conference on Multiphase Flow, Yokohama, Japan, 30 May–4 June 2004.
- Spalding, D.B. PHOENICS Encyclopedia. Models for Two-Phase Flows: Two-Equation k-ε Turbulence Model. Available online: http://www.cham.co.uk/phoenics/d_polis/d_enc/turmod/enc_tu74.htm (accessed on 22 July 2021).
- Elghobashi, S.E.; Abou-Arab, T.W. A two-equation turbulence model for two-phase flows. Phys. Fluids 1983, 26, 931–938.
- Mandø, M.; Lightstone, M.F.; Rosendahl, L.; Yin, C.; Sørensen, H. Turbulence modulation in dilute particle-laden flow. Int. J. Heat Fluid Flow 2009, 30, 331–338.
- Messa, G.V.; Malavasi, S. Numerical prediction of dispersed turbulent liquid–solid flows in vertical pipes. J. Hydraul. Res. 2014, 52, 684–692.
- Kaushal, D.R.; Thinglas, T.; Tomita, Y.; Kuchii, S.; Tsukamoto, H. CFD modeling for pipeline flow of fine particles at high concentration. Int. J. Multiph. Flow 2012, 43, 85–100.
- Johnson, P.C.; Jackson, R. Frictional-collisional constitutive relations for granular materials, with application to plane shearing. J. Fluid Mech. 1987, 176, 67–93.
- Messa, G.V.; Malavasi, S. Improvements in the numerical prediction of fully-suspended slurry flow in horizontal pipes. Powder Technol. 2015, 270, 358–367.
- Manninen, M.; Taivassalo, V.; Kallio, S. On the Mixture Model for Multiphase Flow; VTT Technical Research Centre of Finland: Espoo, Finland, 1996.




