| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Jaroslaw Przewlocki | + 2626 word(s) | 2626 | 2021-08-17 04:53:15 | | | |
| 2 | Vicky Zhou | Meta information modification | 2626 | 2021-08-17 11:46:23 | | | | |
| 3 | Vicky Zhou | + 1 word(s) | 2627 | 2021-08-17 11:47:50 | | |
Video Upload Options
The issue of slope stability is one of the most important and yet most difficult geotechnical problems. Assessing slope stability is particularly difficult because of the many uncertainties involved in the process. To take these uncertainties into account, probabilistic methods are used, and the reliability approach is adopted. There are many methods for reliability assessment of earth slope stability. However, there is no system that would organize all of these methods in an unambiguous way. In fact, these methods can be classified in different ways: by assignment to a deterministic classification of methods, by description of uncertainties of soil parameters, by level of reliability according to the theory of reliability, etc. The huge number of articles summarizing the research in this field, but in various “disordered” directions, certainly do not facilitate the understanding or ultimately the practical application of the reliability approach by the engineer. We propose a universal classification system of reliability methods for evaluating the stability of earth slopes. This proposal is preceded by a brief literature review of both historical background and contemporary study on reliability analysis of earth slope stability.
1. Introduction
This paper proposes a classification system of reliability methods for earth slope stability assessment that integrates deterministic slope stability methods, modelling of uncertain soil parameters and reliability level (commonly used in the structural safety analysis). Also, in the case of the most sophisticated approaches, further divisions related to improvement of computation efficiency are suggested.
2. Methods for Evaluating the Stability of Earth Slopes
3. Classification System
In a structural safety analysis, there are different levels of reliability, depending on the importance of the structure, grouped under four basic levels:
- level 1—partial factor approach — employs only one “characteristic” value of each uncertainty parameter;
- level 2—estimates two values of each uncertainty parameter, usually the mean value, standard deviation, and the correlation between these parameters;
- level 3—best estimate of the probability of failure—knowledge of the join distribution of all uncertain parameters is required;
- level 4—reliability methods appropriate for structures of major economic importance, taking into account the structures’ economic value, including the consequences of their failure.
The level 2 reliability methods are included in limit state design codes. Methods of level 2 include a range of approximate or iterative procedures such as the perturbation method, FOSM, SOSM, FORM, SORM, PEM, etc. Methods of level 3, in the strict sense, require determining the mathematically exact probability of structural failure as a result of integrating the joint probability density function of random variables. In the case of slope stability, they can only be used for simplified, idealised cases. However, in a broader sense, level 3 methods require estimates of all probabilistic measures. The Monte Carlo simulation method has become the dominant procedure here as a result of the rapid development of computer techniques that have taken place in recent years. In order to improve the efficiency of this method while maintaining the accuracy of calculations, various reduction techniques have been developed (e.g., stratified sampling, Latin Hypercube simulation, importance sampling and Russian roulette and splitting). The response surface method and the methods of artificial neural networks have also grown in popularity in the analysis of the reliability of slopes. Both methods allow all probabilistic measures to be estimated and can also be qualified to the level 3 reliability method.
In the deterministic approach to slope stability, three basic approaches—the limit equilibrium method (LEM), the displacement‐based finite/different element method (FEM/DEM), and limit analysis (LA)—have been developed. Probabilistic methods used in geotechnical engineering are commonly divided into two groups, depending on the description of the uncertainties of the soil parameters: the single random variable (SRV) approach and the random field (RF) approach.
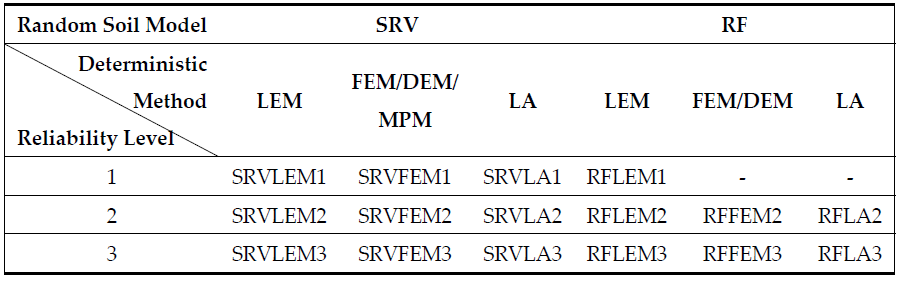
The proposal of a classification of reliability methods of slope stability is presented the Table 1. It combines deterministic methods of slope stability with random modelling of the soil medium and includes levels of reliability.
Table 1. Classification of reliability methods of earth slope stability.
The abbreviations in Table 1 refer to the random soil model, deterministic slope stability method and reliability level. For example: SRVLEM1—soil modelled as a single random variable (SRV), limit equilibrium method (LEM) and Level 1 reliability method; RFFEM3—soil modelled as a random field, finite/different element method and Level 3 reliability method; etc.
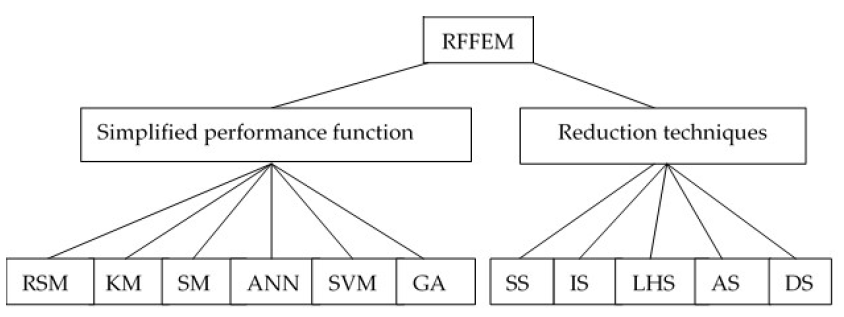
Currently, the FEM/DEM is the predominant deterministic method of stability assessment, soil is usually modelled as a random field and level 3 reliability methods are usually applied. Most of the research focus here is on computation efficiency. Thus, the RFFEM3 methods can be divided into two groups depending on how the performance function of slope stability is simplified and on the reduction techniques (Figure 1).
Figure 1. Division of RFFEM3 methods. RSM—response surface method. Improved RSM methods: KM—Kriging methodology, SM—surrogate models, ANN—artificial neural network, SVM—support vector machine, GA—genetic algorithms, SS—subset simulation, IS—importance sampling, LHS—Latin Hypercube sampling, AS—adaptive sampling, DS—directional simulation.
Slopes can be subjected both to static (gravity) and dynamic (earthquake, waves) loads as well as environmental loads (rainfall, temperature changes). Also, slope failure modelling can be carried out in a two‐dimensional or three‐dimensional analysis. However, these factors should not affect the proposed classification system of reliability methods. Instead, new subdivisions could be introduced on their basis.
4. Conclusions
This literature review shows that although reliability methods are extremely advanced and the computational possibilities almost unlimited, in practice, the simplest methods are usually used. This is mainly due to the fact that engineers are not familiar with probabilistic concepts; thus, it is difficult to incorporate them into practice.
References
- Fellenius, W. Calculations of the Stability of Earth Dams. In Proceedings of the Second Congress of Large Dams, Washington, DC, USA, 7–12 September 1936; Volume 4, pp. 445–463.
- Bishop, A.W. The use of the slip circle in the stability analysis of slopes. Geotechnique 1955, 5, 7–17.
- Janbu, N. Slope Stability Computation, Embankment- Dam Engineering: Casagrande Volume; John Wiley & Sons: New York, NY, USA, 1973; pp. 47–86.
- Nonveiller, E. The stability analysis of slopes with a slide surface of general shape. In Proceedings of the 6th International Conference on Soil Mechanics and Foundation Engineering, Montreal, QC, Canada, 8–15 September 1965; Volume 2, pp. 522–525.
- Spencer, E. A method of analysis of the stability of embankments assuming parallel inter-slice forces. Geotechnique 1967, 17, 11–26.
- Morgenstern, N.R.; Price, V.E. The Analysis of the Stability of General Slip Surfaces. Geotechnique 1965, 15, 77–93.
- Zienkiewicz, O.C.; Humpheson, C.; Lewis, R.W. Associated and Non-Associated Visco-Plasticity and Plasticity in Soil Mechanics. Geotechnique 1975, 25, 671–689.
- Dawson, E.M.; Roth, W.H.; Drescher, A. Slope Stability Analysis by Strength Reduction. Geotechnique 1999, 49, 835–840.
- Griffiths, D.V.; Lane, P.A. Slope stability analysis by finite elements. Geotechnics 1999, 49, 387–403.
- Cheng, Y.M. Location of critical failure surface and some further studies on slope stability analysis. Comput. Geotech. 2003, 30, 255–267.
- Drucker, D.C.; Prager, W. Soil mechanics and plastic analysis or limit design. Q. Appl. Math. 1952, 10, 157–165.
- Chen, W.F.; Giger, M.W.; Fang, H.Y. On the limit analysis of stability of slopes. Soils Found. 1969, 9, 23–32.
- Donald, I.B.; Chen, Z.Y. Slope stability analysis by the upper bound approach: Fundamentals and methods. Can. Geotech. J. 1997, 34, 853–862.
- Michalowski, R.L. Slope stability analysis: A kinematical approach. Géotechnique 1995, 45, 283–293.
- Przewłócki, J. Some comments on slope stability evaluation. Part I: Deterministic analysis. Inżynieria Morska Geotech. 2004, 2, 141–149.
- Wu, T.H.; Kraft, L.M. Safety Analysis of Slopes. J. Soil Mech. Found. Div. 1970, 96, 609–630.
- Cornell, C.A. First-order uncertainty analysis of soil deformation and stability. In Proceedings of the 1st International Conference Applications of Statistics and Probability in Soil and Structural, Hong Kong, 13–16 September 1971; pp. 129–144. Available online: https://trid.trb.org/view/128568 (accessed on 16 July 1974).
- Alonso, E.E. Risk analysis of slopes and its application to slopes in Canadian sensitive clays. Geotechique 1976, 26, 453–472.
- Tang, W.H.; Yucemen, M.S.; Ang, A.H.S. Probability based short term design of soil slopes. Can. Geotech. J. 1976, 13, 201–215.
- Vanmarcke, E.H. Reliability of earth slopes. J. Geotech. Eng. 1977, 103, 1227–1246.
- Chowdhury, R.N.; Grivas, D. Probabilistic model of progressive failure of slopes. J. Geot. Eng. 1982, 108, 803–917.
- Tobutt, D.C. Monte Carlo simulation methods for slope stability. Comput. Geosci. 1982, 8, 199–209.
- Chowdhury, R.N.; Tang, W.H.; Sidi, I. Reliability model of progressive slope failure. Géotechnique 1987, 37, 467–481.
- El-Ramly, H.; Morgenstern, N.R.; Cruden, D.M. Probabilistic slope stability analysis for practice. Can. Geotech. 2002, 39, 665–683.
- Griffiths, D.V.; Fenton, G.A. Probabilistic Slope Stability Analysis by Finite Elements. J. Geotech. Geoenviron. Eng. 2004, 130, 507–518.
- Christian, J.T.; Ladd, C.C.; Baecher, G.B. Reliability applied to slope stability analysis. J. Geot. Eng. 1994, 120, 2180–2207.
- Hassan, A.M.; Wolff, T.F. Search algorithm for minimum reliability index of earth slopes. J. Geotech. Geoenviron. Eng. 1999, 125, 301–308.
- Low, B.K.; Tang, W.H. Probabilistic Slope Analysis Using Janbu’s Generalized Procedure of Slices. Comput. Geotech. 1997, 21, 121–142.
- Low, B.K.; Gilbert, R.B.; Wright, S.G. Slope reliability analysis using generalized method of slices. J. Geotech. Geoenviron. Eng. 1998, 124, 350–362.
- Cho, S.E. Effects of spatial variability of soil properties on slope stability. Eng. Geol. 2007, 92, 97–109.
- Cho, S.E. First-order reliability analysis of slope considering multiple failure modes. Eng. Geol. 2013, 154, 98–105.
- Knabe, W.; Przewłócki, J. Probabilistic Slope Stability Analysis; Institute of Hydro-Engineering of Polish Academy of Sciences: Gdańsk, Poland, 1990.
- Przewłócki, J. Some comments on slope stability evaluation. Part II: Probabilistic analysis. Inżynieria Morska Geotech. 2004, 3, 141–149.