Video Upload Options
Compliant continuum robots (CCRs) are usually made of elastic materials, including nitinol alloy (NiTi), silicone, rubberand polyamide, etc. They are designed to be slender, i.e., low diameter to length ratio. CCRs have been widely employed in a constraint environment to manipulate tasks, such as minimally invasive cardiac surgery, orthopaedic surgery, endoscopic surgery, bariatric surgeryand the inspection of gas turbine engines, in-situ aero-engine maintenance works.
1. Introduction
CCRs have been widely employed in a constraint environment to manipulate tasks, such as minimally invasive cardiac surgery [1], orthopaedic surgery [2][3][4], endoscopic surgery [5], bariatric surgery [6] and the inspection of gas turbine engines [7], in-situ aero-engine maintenance works [8][9][10][11]. Researchers usually classify CCRs in two ways, one is the drive system classification, including tendon-driven robots, cable-driven robots, pneumatic robots, shape-memory-alloy robots. In this paper, we classify the CCRs into two groups, including semi-soft continuum robots and soft continuum robots. sometimes rigid disks or rods are added to increase rigidity [12].
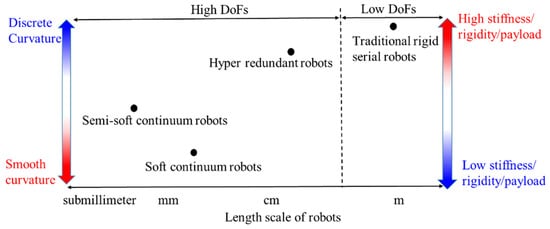
Traditional serial robots consist of rigid links and rigid joints. The comparison between continuum robots and rigid serial robots is shown in Figure 1, including the curvature of a robot’s shape, size, stiffness and degrees of freedom (DoFs). Semi-soft continuum robots have a minimal scale compared with others; recently a magnetic soft submillimetre scale continuum robot blurs the line between the semi-soft continuum robot and the soft continuum robot, as the magnetic fluid can turn into an elastic solid under a magnetic field [13]. Remaining a high stiffness and a smooth curvature are the aims for designing a continuum robot.
2. Trends and Classifications of CCRs

| Descriptions | ||
|---|---|---|
| Characteristics | basic transmission units | Basic motion units of CCRs. |
| drive systems | Actuation force/moment systems, such as the pull-push force, the pneumatic pressure, the hydric pressure and the magnetic force, etc. | |
| stiffness | Stiffness is the rigidity of a CCR. Including variable stiffness and constant stiffness. | |
| sensing systems | The accuracy of motions increases with the feedbacks of the sensing systems, including external sensors and intrinsic sensing. | |
| Problems | frictions | Frictions between component units, such as frictions between cable and disk holes. |
| buckling | The stiffness suddenly decreases to quasi-zero, when a compressing load acts the CCR. | |
| singularity | The ill Jacobian matrices between the inputs and outputs. | |
| twisting | Both torques generated by the CCR weight and the payload influence the tip position. |
3. Different Basic Transmission Units and Drive Systems
3.1. Basic Transmission Units
3.1.1. Backbone CCRs
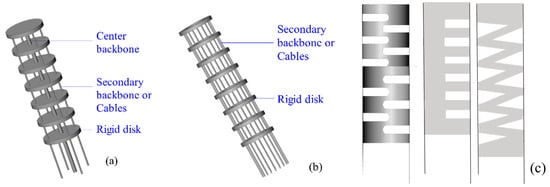
3.1.2. Soft-Tube CCRs
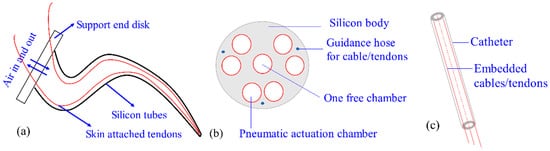
3.1.3. Concentric-Tube CCRs
3.1.4. Spring CCRs
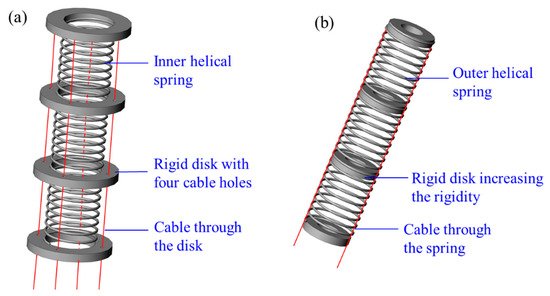
3.1.5. Compliant-Joint CCRs
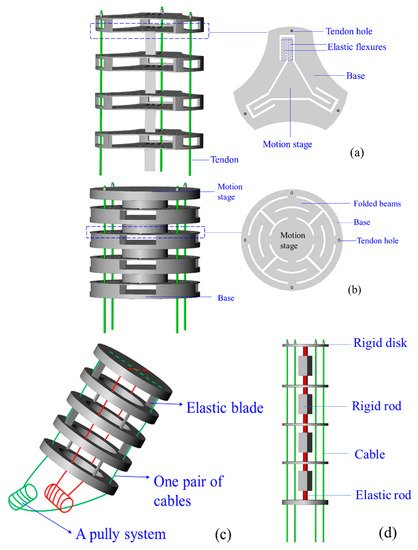
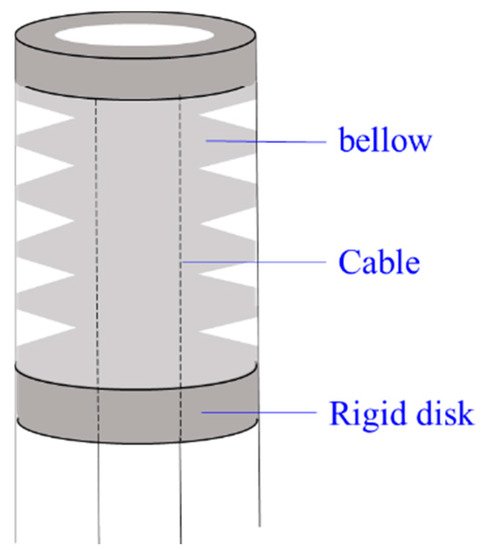
3.1.6. Bellow CCRs
3.1.7. Origami CCRs
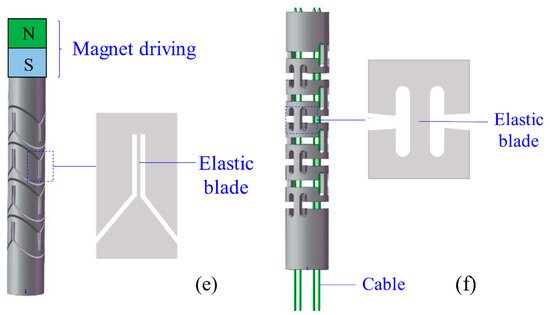
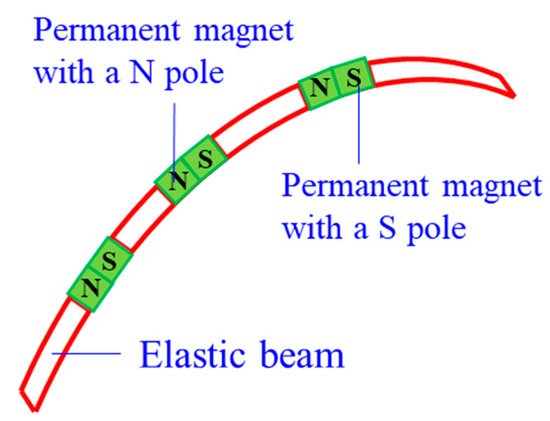
3.1.8. Magnet CCRs
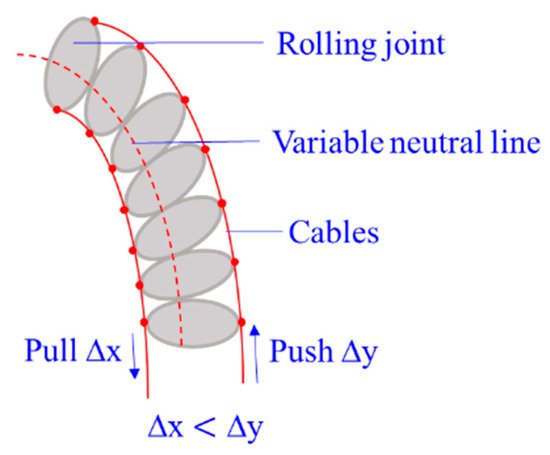
3.1.9. Rolling-Joint CCRs
3.1.10. Braid CCRs
3.1.11. Hybrid CCRs
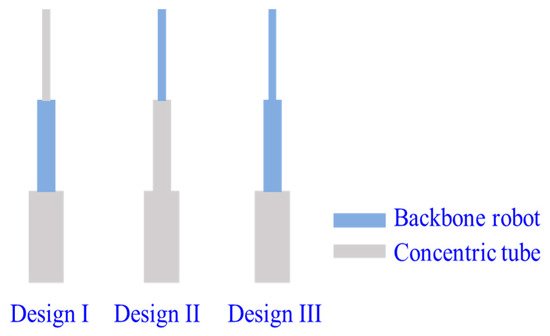
-
Backbone-Concentric-Tube CCR
-
Backbone-Bellow CCR
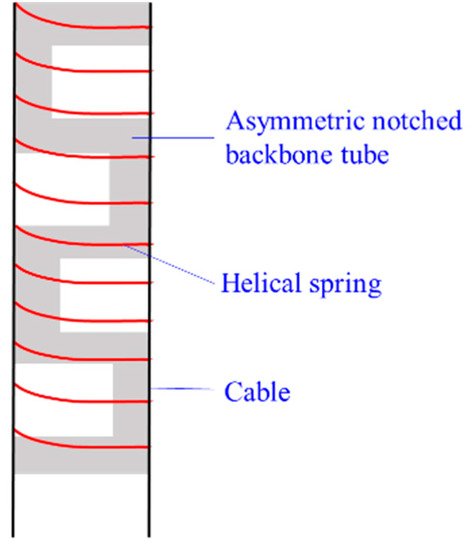
-
Notched Backbone-Spring CCR
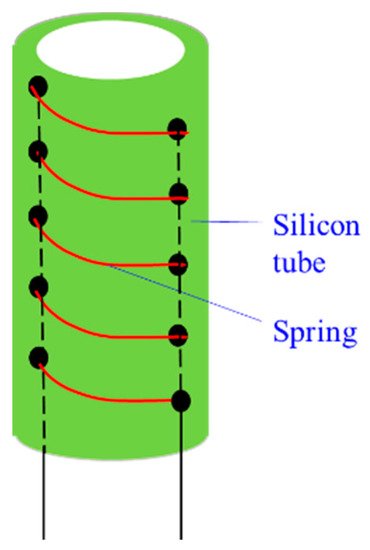
-
Soft tube-Spring CCR
-
Soft tube-Origami manipulator
3.2. Drive Systems
| Drive Systems | Advantages | Disadvantages |
|---|---|---|
| Cable/tendon | Exert large force; easy control; large ratio of power to weight. | Cable slack; cable coupling; friction between cables and disks. |
| Backbone | Remote actuation; fewer actuation wires; reduce buckling. | Backlash; frictions between actuation lines and conduits; extension and compression of actuating backbones. |
| Pneumatic | Exert large force; variable stiffness by regulating air pressure; large ratio of power to weight. | Strong nonlinearities of a kinematic model; not safe enough if the air leak. |
| Hydraulic | Exert large force. | The extra weight of fluid; failure of the hydraulic power supply. |
| Magnet | No surface contact; lightweight; Tether-free actuation; sub-millimetre scale. |
Complex electromagnets control. |
| SMA | Certain shape curvature. | Need efficient cooling system; sensitive to environment temperature; slow response speed. |
| EPA | Lightweight; small scale. | Low actuation pressure; required high input voltage; limited range motion. |
References
- Yip, M.C.; Camarillo, D.B. Model-Less Hybrid Position/Force Control: A Minimalist Approach for Continuum Manipulators in Unknown, Constrained Environments. IEEE Robot. Autom. Lett. 2016, 1, 844–851.
- Alambeigi, F.; Bakhtiarinejad, M.; Sefati, S.; Hegeman, R.; Iordachita, I.; Khanuja, H.; Armand, M. On the Use of a Continuum Manipulator and a Bendable Medical Screw for Minimally Invasive Interventions in Orthopedic Surgery. IEEE Trans. Med. Robot. Bionics 2019, 1, 14–21.
- Roy, R.; Wang, L.; Simaan, N. Modeling and Estimation of Friction, Extension, and Coupling Effects in Multisegment Continuum Robots. IEEE/ASME Trans. Mechatron. 2016, 22, 909–920.
- Gao, A.; Murphy, R.J.; Liu, H.; Iordachita, I.I.; Armand, M. Mechanical Model of Dexterous Continuum Manipulators With Compliant Joints and Tendon/External Force Interactions. IEEE/ASME Trans. Mechatron. 2017, 22, 465–475.
- Kato, T.; Okumura, I.; Song, S.-E.; Golby, A.J.; Hata, N. Tendon-Driven Continuum Robot for Endoscopic Surgery: Preclinical Development and Validation of a Tension Propagation Model. IEEE/ASME Trans. Mechatron. 2015, 20, 2252–2263.
- Zhang, X.; Li, W.; Chiu, P.W.-Y.; Li, Z. A Novel Flexible Robotic Endoscope With Constrained Tendon-Driven Continuum Mechanism. IEEE Robot. Autom. Lett. 2020, 5, 1366–1372.
- Dong, X.; Axinte, D.; Palmer, D.; Cobos, S.; Raffles, M.; Rabani, A.; Kell, J. Development of a slender continuum robotic system for on-wing inspection/repair of gas turbine engines. Robot. Comput. Manuf. 2017, 44, 218–229.
- Hannan, M.W.; Walker, I.D. Analysis and experiments with an elephant’s trunk robot. Adv. Robot. 2001, 15, 847–858.
- Zheng, T.; Branson, D.T.; Kang, R.; Cianchetti, M.; Guglielmino, E.; Follador, M.; Medrano-Cerda, G.A.; Godage, I.S.; Caldwell, D.G. Dynamic continuum arm model for use with underwater robotic manipulators inspired by octopus vulgaris. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2012; pp. 5289–5294.
- Porter, M.M.; Adriaens, D.; Hatton, R.L.; Meyers, M.A.; McKittrick, J. Why the seahorse tail is square. Science 2015, 349.
- Li, L.; Jin, T.; Tian, Y.; Yang, F.; Xi, F. Design and Analysis of a Square-Shaped Continuum Robot With Better Grasping Ability. IEEE Access 2019, 7, 57151–57162.
- Dong, X.; Raffles, M.; Cobos-Guzmán, S.; Axinte, D.; Kell, J. A Novel Continuum Robot Using Twin-Pivot Compliant Joints: Design, Modeling, and Validation. J. Mech. Robot. 2015, 8, 021010.
- Kim, Y.; Parada, G.A.; Liu, S.; Zhao, X. Ferromagnetic soft continuum robots. Sci. Robot. 2019, 4, eaax7329.
- Hannan, M.W.; Walker, I.D. Kinematics and the Implementation of an Elephant’s Trunk Manipulator and Other Continuum Style Robots. J. Robot. Syst. 2003, 20, 45–63.
- Xu, K.; Simaan, N. An Investigation of the Intrinsic Force Sensing Capabilities of Continuum Robots. IEEE Trans. Robot. 2008, 24, 576–587.
- Bajo, A.; Simaan, N. Hybrid motion/force control of multi-backbone continuum robots. Int. J. Robot. Res. 2015, 35, 422–434.
- Shen, W.; Yang, G.; Zheng, T.; Wang, Y.; Yang, K.; Fang, Z. An Accuracy Enhancement Method for a Cable-Driven Continuum Robot With a Flexible Backbone. IEEE Access 2020, 8, 37474–37481.
- Langer, M.; Amanov, E.; Burgner-Kahrs, J. Stiffening Sheaths for Continuum Robots. Soft Robot. 2018, 5, 291–303.
- Ouyang, B.; Liu, Y.; Tam, H.Y.; Sun, N. Design of an Interactive Control System for a Multisection Continuum Robot. IEEE/ASME Trans. Mechatron. 2018, 23, 2379–2389.
- Case, J.C.; White, E.L.; SunSpiral, V.; Kramer-Bottiglio, R. Reducing Actuator Requirements in Continuum Robots Through Optimized Cable Routing. Soft Robot. 2018, 5, 109–118.
- Oliver-Butler, K.; Till, J.; Rucker, C. Continuum Robot Stiffness Under External Loads and Prescribed Tendon Displacements. IEEE Trans. Robot. 2019, 35, 403–419.
- Ma, X.; Song, C.; Chiu, W.Y.P.; Li, Z. Autonomous Flexible Endoscope for Minimally Invasive Surgery With Enhanced Safety. IEEE Robot. Autom. Lett. 2019, 4, 2607–2613.
- Gravagne, I.A.; Rahn, C.D.; Walker, I.D.; Member, S. Large Deflection Dynamics and Control for Planar Continuum Robots. IEEE/ASME Trans. Mechatron. 2003, 8, 299–307.
- Rucker, D.C.; Webster, R.J. Statics and dynamics of continuum robots with general tendon routing and external loading. IEEE Trans. Robot. 2011, 27, 1033–1044.
- Gravagne, I.A.; Walker, I.D. Manipulability, force, and compliance analysis for planar continuum manipulators. IEEE Trans. Robot. Autom. 2002, 18, 263–273.
- Chikhaoui, M.T.; Lilge, S.; Kleinschmidt, S.; Burgner-Kahrs, J. Comparison of Modeling Approaches for a Tendon Actuated Continuum Robot With Three Extensible Segments. IEEE Robot. Autom. Lett. 2019, 4, 989–996.
- Xu, K.; Zhao, J.; Qiu, D.; Wang, Y. A Pilot Study of a Continuum Shoulder Exoskeleton for Anatomy Adaptive Assistances. J. Mech. Robot. 2014, 6, 041011.
- Rone, W.S.; Ben-Tzvi, P. Mechanics Modeling of Multisegment Rod-Driven Continuum Robots. J. Mech. Robot. 2014, 6, 041006.
- Goldman, R.E.; Bajo, A.; Simaan, N. Compliant Motion Control for Multisegment Continuum Robots With Actuation Force Sensing. IEEE Trans. Robot. 2014, 30, 890–902.
- Rone, W.S.; Ben-Tzvi, P. Continuum Robot Dynamics Utilizing the Principle of Virtual Power. IEEE Trans. Robot. 2014, 30, 275–287.
- Xu, K.; Zhao, J.; Fu, M. Development of the SJTU Unfoldable Robotic System (SURS) for Single Port Laparoscopy. IEEE/ASME Trans. Mechatron. 2014, 20, 2133–2145.
- Li, Z.; Zin Oo, M.; Nalam, V.; Duc Thang, V.; Ren, H.; Kofidis, T.; Yu, H. Design of a novel flexible endoscope-cardioscope. J. Mech. Robot. 2016, 8, 1–9.
- Yuan, H.; Chiu, P.W.Y.; Li, Z. Shape-Reconstruction-Based Force Sensing Method for Continuum Surgical Robots With Large Deformation. IEEE Robot. Autom. Lett. 2017, 2, 1972–1979.
- Moses, M.S.; Murphy, R.J.; Kutzer, M.D.M.; Armand, M. Modeling Cable and Guide Channel Interaction in a High-Strength Cable-Driven Continuum Manipulator. IEEE/ASME Trans. Mechatron. 2015, 20, 2876–2889.
- Yoshida, S.; Kanno, T.; Kawashima, K. Surgical Robot With Variable Remote Center of Motion Mechanism Using Flexible Structure. J. Mech. Robot. 2018, 10, 031011.
- Du, Z.; Yang, W.; Dong, W. Kinematics Modeling of a Notched Continuum Manipulator. J. Mech. Robot. 2015, 7, 041017.
- Kutzer, M.D.; Segreti, S.M.; Brown, C.Y.; Armand, M.; Taylor, R.H.; Mears, S.C. Design of a new cable-driven manipulator with a large open lumen: Preliminary applications in the minimally-invasive removal of osteolysis. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011.
- He, B.; Wang, Z.; Li, Q.; Xie, H.; Shen, R. An Analytic Method for the Kinematics and Dynamics of a Multiple-Backbone Continuum Robot. Int. J. Adv. Robot. Syst. 2013, 10, 84.
- Guo, H.; Ju, F.; Cao, Y.; Qi, F.; Bai, D.; Wang, Y.; Chen, B. Continuum robot shape estimation using permanent magnets and magnetic sensors. Sens. Actuators A Phys. 2019, 285, 519–530.
- Ouyang, B.; Liu, Y.; Sun, D. Design of a three-segment continuum robot for minimally invasive surgery. Robot. Biomim. 2016, 3, 43.
- Zhao, B.; Zeng, L.; Wu, Z.; Xu, K. A continuum manipulator for continuously variable stiffness and its stiffness control formulation. Mech. Mach. Theory 2020, 149, 103746.
- Xu, K.; Fu, M.; Zhao, J. An experimental kinestatic comparison between continuum manipulators with structural variations. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2014; pp. 3258–3264.
- Zheng, T.; Branson, D.T.; Guglielmino, E.; Kang, R.; Cerda, G.A.M.; Cianchetti, M.; Follador, M.; Godage, I.S.; Caldwell, D.G. Model Validation of an Octopus Inspired Continuum Robotic Arm for Use in Underwater Environments. J. Mech. Robot. 2013, 5, 021004.
- Renda, F.; Giorelli, M.; Calisti, M.; Cianchetti, M.; Laschi, C. Dynamic Model of a Multibending Soft Robot Arm Driven by Cables. IEEE Trans. Robot. 2014, 30, 1109–1122.
- Shiva, A.; Stilli, A.; Noh, Y.; Faragasso, A.; De Falco, I.; Gerboni, G.; Cianchetti, M.; Menciassi, A.; Althoefer, K.; Wurdemann, H.A. Tendon-Based Stiffening for a Pneumatically Actuated Soft Manipulator. IEEE Robot. Autom. Lett. 2016, 1, 632–637.
- Dalvand, M.M.; Nahavandi, S.; Howe, R.D. An Analytical Loading Model for n-Tendon Continuum Robots. IEEE Trans. Robot. 2018, 34, 1215–1225.
- Zhang, Z.; Dequidt, J.; Back, J.; Liu, H.; Duriez, C. Motion Control of Cable-Driven Continuum Catheter Robot Through Contacts. IEEE Robot. Autom. Lett. 2019, 4, 1852–1859.
- Kang, R.; Guglielmino, E.; Zullo, L.; Branson, D.T.; Godage, I.; Caldwell, D.G. Embodiment design of soft continuum robots. Adv. Mech. Eng. 2016, 8, 1–13.
- Camarillo, D.B.; Milne, C.F.; Carlson, C.R.; Zinn, M.R.; Salisbury, J.K. Mechanics Modeling of Tendon-Driven Continuum Manipulators. IEEE Trans. Robot. 2008, 24, 1262–1273.
- Hasanzadeh, S.; Janabi-Sharifi, F. An Efficient Static Analysis of Continuum Robots. J. Mech. Robot. 2014, 6, 031011.
- Lotfavar, A.; Hasanzadeh, S.; Janabi-Sharifi, F. Cooperative Continuum Robots: Concept, Modeling, and Workspace Analysis. IEEE Robot. Autom. Lett. 2017, 3, 426–433.
- Yu, B.; Fernández, J.D.G.; Tan, T. Probabilistic Kinematic Model of a Robotic Catheter for 3D Position Control. Soft Robot. 2019, 6, 184–194.
- Kang, R.; Guo, Y.; Chen, L.; Branson, D.T.; Dai, J.S. Design of a Pneumatic Muscle Based Continuum Robot With Embedded Tendons. IEEE/ASME Trans. Mech. 2016, 22, 751–761.
- Li, M.; Kang, R.; Branson, D.T.; Dai, J.S. Model-Free Control for Continuum Robots Based on an Adaptive Kalman Filter. IEEE/ASME Trans. Mechatron. 2017, 23, 286–297.
- Wang, Y.; Gregory, C.; Minor, M.A. Improving Mechanical Properties of Molded Silicone Rubber for Soft Robotics Through Fabric Compositing. Soft Robot. 2018, 5, 272–290.
- Webster, R.J.; Okamura, A.M.; Cowan, N.J. Toward Active Cannulas: Miniature Snake-Like Surgical Robots. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 2857–2863.
- Morimoto, T.K.; Okamura, A.M. Design of 3-D Printed Concentric Tube Robots. IEEE Trans. Robot. 2016, 32, 1419–1430.
- Bergeles, C.; Gosline, A.H.; Vasilyev, N.V.; Codd, P.J.; Del Nido, P.J.; Dupont, P.E. Concentric Tube Robot Design and Optimization Based on Task and Anatomical Constraints. IEEE Trans. Robot. 2015, 31, 67–84.
- Dupont, P.E.; Lock, J.; Itkowitz, B.; Butler, E.J. Design and Control of Concentric-Tube Robots. IEEE Trans. Robot. 2010, 26, 209–225.
- Iyengar, K.; Dwyer, G.; Stoyanov, D. Investigating exploration for deep reinforcement learning of concentric tube robot control. Int. J. Comput. Assist. Radiol. Surg. 2020, 15, 1157–1165.
- Su, H.; Li, G.; Rucker, D.C.; Iii, R.J.W.; Fischer, G.S. A Concentric Tube Continuum Robot with Piezoelectric Actuation for MRI-Guided Closed-Loop Targeting. Ann. Biomed. Eng. 2016, 44, 2863–2873.
- Webster, I.R.J.; Romano, J.M.; Cowan, N.J. Mechanics of Precurved-Tube Continuum Robots. IEEE Trans. Robot. 2009, 25, 67–78.
- Hendrick, R.J.; Gilbert, H.B.; Webster, R.J. Designing snap-free concentric tube robots: A local bifurcation approach. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 25–30 May 2015; pp. 2256–2263.
- Gilbert, H.B.; Hendrick, R.J.; Iii, R.J.W. Elastic Stability of Concentric Tube Robots: A Stability Measure and Design Test. IEEE Trans. Robot. 2016, 32, 20–35.
- Rucker, D.C.; Webster, I.R.J.; Chirikjian, G.S.; Cowan, N.J. Equilibrium Conformations of Concentric-tube Continuum Robots. Int. J. Robot. Res. 2010, 29, 1263–1280.
- Kudryavtsev, A.V.; Chikhaoui, M.T.; Liadov, A.; Rougeot, P.; Spindler, F.; Rabenorosoa, K.; Burgner-Kahrs, J.; Tamadazte, B.; Andreff, N. Eye-in-Hand Visual Servoing of Concentric Tube Robots. IEEE Robot. Autom. Lett. 2018, 3, 2315–2321.
- Vandini, A.; Bergeles, C.; Glocker, B.; Giataganas, P.; Yang, G.-Z. Unified Tracking and Shape Estimation for Concentric Tube Robots. IEEE Trans. Robot. 2017, 33, 901–915.
- Xu, R.; Yurkewich, A.; Patel, R.V. Curvature, Torsion, and Force Sensing in Continuum Robots Using Helically Wrapped FBG Sensors. IEEE Robot. Autom. Lett. 2016, 1, 1052–1059.
- Haraguchi, D.; Kanno, T.; Tadano, K.; Kawashima, K. A Pneumatically Driven Surgical Manipulator With a Flexible Distal Joint Capable of Force Sensing. IEEE/ASME Trans. Mechatron. 2015, 20, 2950–2961.
- Li, M.; Kang, R.; Geng, S.; Guglielmino, E. Design and control of a tendon-driven continuum robot. Trans. Inst. Meas. Control. 2018, 40, 3263–3272.
- Yoon, H.-S.; Jeong, J.H.; Yi, B.-J. Image-Guided Dual Master–Slave Robotic System for Maxillary Sinus Surgery. IEEE Trans. Robot. 2018, 34, 1098–1111.
- Santiago, J.L.C.; Godage, I.S.; Gonthina, P.; Walker, I.D. Soft Robots and Kangaroo Tails: Modulating Compliance in Continuum Structures Through Mechanical Layer Jamming. Soft Robot. 2016, 3, 54–63.
- Kim, Y.; Cheng, S.S.; Diakite, M.; Gullapalli, R.P.; Simard, J.M.; Desai, J.P. Toward the Development of a Flexible Mesoscale MRI-Compatible Neurosurgical Continuum Robot. IEEE Trans. Robot. 2017, 33, 1386–1397.
- Gao, A.; Zou, Y.; Wang, Z.; Liu, H. A General Friction Model of Discrete Interactions for Tendon Actuated Dexterous Manipulators. J. Mech. Robot. 2017, 9, 041019.
- Frazelle, C.G.; Kapadia, A.D.; Walker, I.D. A Haptic Continuum Interface for the Teleoperation of Extensible Continuum Manipulators. IEEE Robot. Autom. Lett. 2020, 5, 1875–1882.
- Feng, F.; Hong, W.; Xie, L. Design of 3D-Printed Flexible Joints With Presettable Stiffness for Surgical Robots. IEEE Access 2020, 8, 79573–79585.
- Francis, P.; Eastwood, K.W.; Bodani, V.; Price, K.; Upadhyaya, K.; Podolsky, D.; Azimian, H.; Looi, T.; Drake, J. Miniaturized Instruments for the da Vinci Research Kit: Design and Implementation of Custom Continuum Tools. IEEE Robot. Autom. Mag. 2017, 24, 24–33.
- Thuruthel, T.G.; Falotico, E.; Manti, M.; Pratesi, A.; Cianchetti, M.; Laschi, C. Learning Closed Loop Kinematic Controllers for Continuum Manipulators in Unstructured Environments. Soft Robot. 2017, 4, 285–296.
- Frazelle, C.G.; Kapadia, A.; Walker, I. Developing a Kinematically Similar Master Device for Extensible Continuum Robot Manipulators. ASME J. Mech. Robot. 2018, 10, 025005.
- Yeshmukhametov, A.; Buribayev, Z.; Amirgaliyev, Y.; Ramakrishnan, R.R. Modeling and Validation of New Continuum Robot Backbone Design With Variable Stiffness Inspired from Elephant Trunk. IOP Conf. Series Mater. Sci. Eng. 2018, 417, 012010.
- Hao, G.; Dai, F.; He, X.; Liu, Y. Design and analytical analysis of a large-range tri-symmetrical 2R1T compliant mechanism. Microsyst. Technol. 2017, 23, 4359–4366.
- Simaan, N.; Taylor, R.; Flint, P. A dexterous system for laryngeal surgery. In Proceedings of the IEEE International Conference on Robotics and Automation, 2004. ICRA ’04. 2004, New Orleans, LA, USA, 26 April–1 May 2004.
- Qi, P.; Qiu, C.; Liu, H.; Dai, J.S.; Seneviratne, L.; Althoefer, K.A. A Novel Continuum Manipulator Design Using Serially Connected Double-Layer Planar Springs. IEEE/ASME Trans. Mechatron. 2015, 21, 1281–1292.
- Awtar, S.; Slocum, A.H. Flexure systems based on a symmetric diaphragm flexure. In Proceedings of the ASPE 2005 Annual Meeting, Chicago, IL, USA, 10–14 September 2005.
- Dong, X.; Raffles, M.; Guzman, S.C.; Axinte, D.; Kell, J. Design and analysis of a family of snake arm robots connected by compliant joints. Mech. Mach. Theory 2014, 77, 73–91.
- Thomas, T.L.; Venkiteswaran, V.K.; Ananthasuresh, G.K.; Misra, S. A Monolithic Compliant Continuum Manipulator: A Proof-of-Concept Study. J. Mech. Robot. 2020, 12, 1–11.
- Zhang, T.; Ping, Z.; Zuo, S. Miniature Continuum Manipulator with 3-DOF Force Sensing for Retinal Microsurgery. J. Mech. Robot. 2021, 1–34.
- Walker, I.D. Continuous Backbone ‘Continuum’ Robot Manipulators. ISRN Robot. 2013, 2013, 1–19.
- Rolf, M.; Steil, J.J. Efficient Exploratory Learning of Inverse Kinematics on a Bionic Elephant Trunk. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1147–1160.
- Bailly, Y.; Amirat, Y.; Fried, G. Modeling and Control of a Continuum Style Microrobot for Endovascular Surgery. IEEE Trans. Robot. 2011, 27, 1024–1030.
- Kim, S.-J.; Lee, D.-Y.; Jung, G.-P.; Cho, K.-J. An origami-inspired, self-locking robotic arm that can be folded flat. Sci. Robot. 2018, 3, eaar2915.
- Edmondson, B.J.; Bowen, L.A.; Grames, C.L.; Magleby, S.P.; Howell, L.L.; Bateman, T.C. Oriceps: Origami-Inspired Forceps. In Proceedings of the ASME 2013 Conference on Smart Materials, Adaptive Structures and Intelligent Systems. Volume 1: Development and Characterization of Multifunctional Materials; Modeling, Simulation and Control of Adaptive Systems; Integrated System Design and Implementation, Snowbird, UT, USA, 16–18 September 2013.
- Zhang, K.; Qiu, C.; Dai, J.S. An Extensible Continuum Robot With Integrated Origami Parallel Modules. J. Mech. Robot. 2016, 8, 031010.
- Edelmann, J.; Petruska, A.J.; Nelson, B.J. Magnetic control of continuum devices. Int. J. Robot. Res. 2017, 36, 68–85.
- Suh, J.-W.; Kim, K.-Y.; Jeong, J.-W.; Lee, J.-J. Design Considerations for a Hyper-Redundant Pulleyless Rolling Joint With Elastic Fixtures. IEEE/ASME Trans. Mechatron. 2015, 20, 2841–2852.
- Kim, Y.-J.; Cheng, S.; Kim, S.; Iagnemma, K. A Stiffness-Adjustable Hyperredundant Manipulator Using a Variable Neutral-Line Mechanism for Minimally Invasive Surgery. IEEE Trans. Robot. 2014, 30, 382–395.
- Hassan, T.; Cianchetti, M.; Mazzolai, B.; Laschi, C.; Dario, P. Active-Braid, a Bioinspired Continuum Manipulator. IEEE Robot. Autom. Lett. 2017, 2, 2104–2110.
- Felt, W.; Chin, K.Y.; Remy, C.D. Contraction Sensing With Smart Braid McKibben Muscles. IEEE/ASME Trans. Mechatron. 2016, 21, 1201–1209.
- Wu, L.; Crawford, R.; Roberts, J. Dexterity Analysis of Three 6-DOF Continuum Robots Combining Concentric Tube Mechanisms and Cable-Driven Mechanisms. IEEE Robot. Autom. Lett. 2016, 2, 514–521.
- Xing, Z.; Wang, F.; Ji, Y.; McCoul, D.; Wang, X.; Zhao, J. A Structure for Fast Stiffness-Variation and Omnidirectional-Steering Continuum Manipulator. IEEE Robot. Autom. Lett. 2021, 6, 755–762.
- Li, S.; Stampfli, J.J.; Xu, H.J.; Malkin, E.; Diaz, E.V.; Rus, D.; Wood, R.J. A vacuum-driven origami ‘magic-ball’ soft gripper. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 7401–7408.
- Simaan, N. Snake-Like Units Using Flexible Backbones and Actuation Redundancy for Enhanced Miniaturization. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 3012–3017.
- Dong, X.; Palmer, D.; Axinte, D.; Kell, J. In-situ repair/maintenance with a continuum robotic machine tool in confined space. J. Manuf. Process. 2019, 38, 313–318.
- Kim, Y.; Cheng, S.S.; Desai, J.P. Active Stiffness Tuning of a Spring-Based Continuum Robot for MRI-Guided Neurosurgery. IEEE Trans. Robot. 2017, 34, 18–28.
- Yang, C.; Geng, S.; Walker, I.; Branson, D.T.; Liu, J.; Dai, J.S.; Kang, R. Geometric constraint-based modeling and analysis of a novel continuum robot with Shape Memory Alloy initiated variable stiffness. Int. J. Robot. Res. 2020, 39, 1620–1634.
- Pelrine, R.E.; Kornbluh, R.D.; Joseph, J.P.; International, S.R.I.; Ave, R.; Park, M. Electrostriction of polymer dielectrics with compliant electrodes as a means of actuation. Sens. Actuators A Phys. 1998, 4247, 77–85.
- Moghadam, A.A.A.; Torabi, K.; Kaynak, A.; Alam, M.N.H.Z.; Kouzani, A.; Mosadegh, B. Control-Oriented Modeling of a Polymeric Soft Robot. Soft Robot. 2016, 3, 82–97.