Your browser does not fully support modern features. Please upgrade for a smoother experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Mykola Sysyn | + 1894 word(s) | 1894 | 2021-07-19 11:02:49 |
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Sysyn, M. Ballasted Track. Encyclopedia. Available online: https://encyclopedia.pub/entry/12178 (accessed on 08 January 2026).
Sysyn M. Ballasted Track. Encyclopedia. Available at: https://encyclopedia.pub/entry/12178. Accessed January 08, 2026.
Sysyn, Mykola. "Ballasted Track" Encyclopedia, https://encyclopedia.pub/entry/12178 (accessed January 08, 2026).
Sysyn, M. (2021, July 19). Ballasted Track. In Encyclopedia. https://encyclopedia.pub/entry/12178
Sysyn, Mykola. "Ballasted Track." Encyclopedia. Web. 19 July, 2021.
Copy Citation
Ballasted track has the phenomenon of local instabilities, which are usually related to the intensive sleeper void development that requires enormous maintenance costs and influences track reliability, availability and safety. The appearance of the void zones is unavoidable in such structures as transition zones, turnouts and rail joints.
ballasted track
unsupported sleepers
sleeper–ballast dynamic impact
dynamic simulation
analytic solution
discrete element modelling
1. Introduction
The maintenance cost reduction using operational and structural measures would require the plausible prediction of void and resulting track geometry development. However, different from the track without voids, the ballast layer settlement behaviour in a void zone is influenced by many factors. The ballast layer in a void zone is subjected to the special dynamic interaction that includes the different frequencies and time-shifted impact oscillations, quasistatic rail loading and contact interaction. The role of the geometrical void parameters is ambiguous (Figure 1): on the one hand, they increase impact loading; on the other hand, they could reduce the quasistatic component due to its redistribution to the neighbour sleepers.
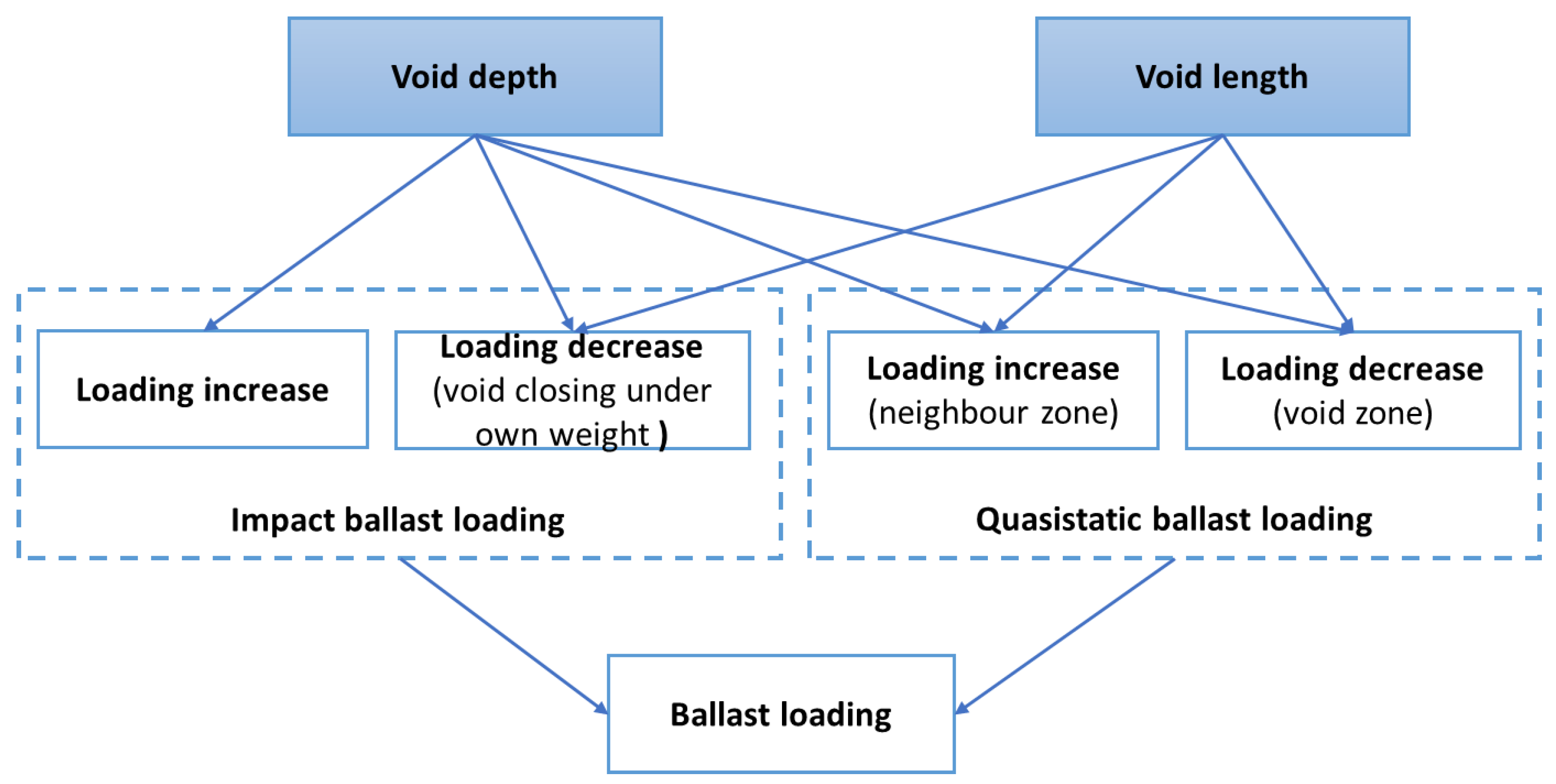 Figure 1. Influence of the void sizes on ballast loading.
Figure 1. Influence of the void sizes on ballast loading.The phenomenon of sleeper–ballast dynamic impact in the void zone can be schematically explained as in Figure 2. After the wheel enters the void zone, the rail-sleeper grid is deflected so that the maximal deflection reaches the void depth. The time moment is the impact moment of the sleeper mass. After that, the void is closed and the ballast is loaded by the quasistatic wheel loading that is, however, to some extent lower than that for the normal track due to the loading redistribution on the neighbour sleepers.
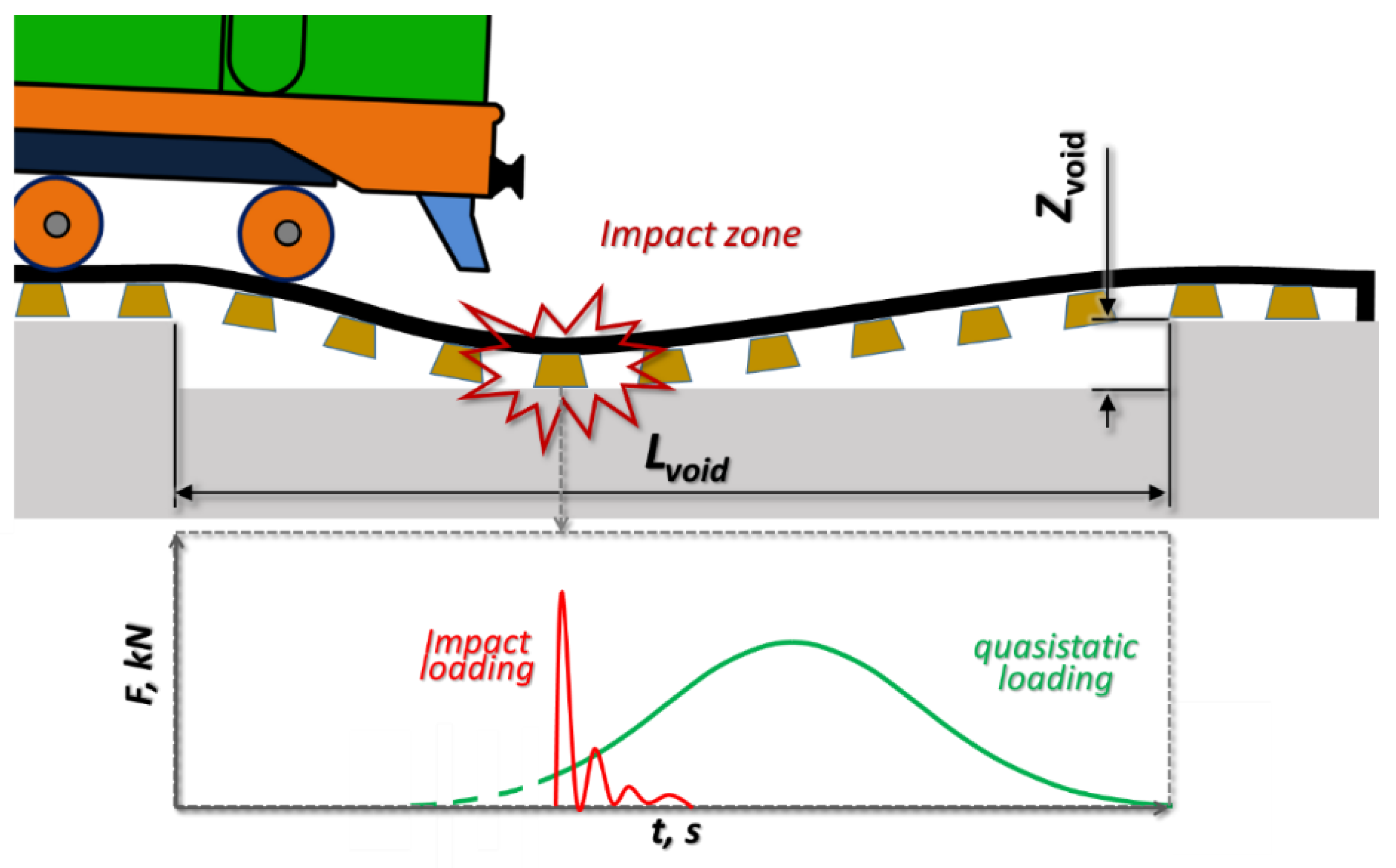 Figure 2. Schematic explanation of the phenomenon of sleeper–ballast dynamic impact in the void zone.
Figure 2. Schematic explanation of the phenomenon of sleeper–ballast dynamic impact in the void zone.The values of the impact and the quasistatic loading depend on the void sizes, trail velocity and other factors.
2. Mechanism of Sleeper–Ballast Dynamic Impact and Residual Settlements Accumulation in Zones with Unsupported Sleepers
There have been many studies on the dynamic interaction in zones with unsupported sleepers. However, most of them are theoretical and generally without experimental comparison and validation.
One of the earliest studies on the dynamic behaviour of railway track with unsupported sleepers is presented in [1]. The dynamic response of railway track with a section of unsupported sleepers was examined experimentally and using a mathematical model. An extensive study on the sleeper void short- and long-term dynamic behaviour is presented in [2]. The applied FEM simulations with the constitutive model of hypoplasticity enabled long-term dynamic settlement prediction of the development of voids between sleeper and ballast. Additionally, the influencing factors of the load level and vibrations were taken into account and the resulting phenomenological settlement equation was proposed. Another theoretical study [3] presents an FEM modelling of the sleeper contact impact due to unsupported sleepers. The modelling simulates several hanging sleepers with a void depth of up to 1 mm. The results indicate an increase of up to 70% in the sleeper–ballast contact force at the neighbouring sleepers for a single hanging sleeper with 1 mm void.
A track system model with hanging sleepers using multibody system (MBS) modelling and finite element method (FEM) techniques is presented in [4]. The influence of the hanging sleepers was assumed in the calculation of the ballast–sleeper interaction as a bilinear function. The model simulated the impact of vibrations due to hanging sleepers on the vehicle and on the track. In [5], the authors present a multibody vehicle–track model assembly that couples the integration of the continuous and discrete system. The model considers an uncontacted spring-damping element underneath the unsupported sleeper as well as a triangularly unsupported sleeper. The presence of a critical gap size causing the largest force was found and was estimated to be 2.5 mm for four unsupported sleepers. An experimental investigation and numerical simulations of the dynamic behaviour of unsupported sleepers are presented in [6]. A simple method for unsupported sleeper identification using a falling weight deflectometer was proposed. The numerical simulations that were based on discrete element modelling showed different loading patterns of fully supported and unsupported sleepers. In [7], the authors investigate the effect of unsupported sleepers on the load of wheel–rail using a numerical simulation based on a coupling dynamic model of vehicle–track.
The vehicle was modelled as a multibody system, and the track was considered as a three-layer model with rails, sleepers and ballast masses. A nonlinear spring and damper were used to simulate a gap between the unsupported sleeper and the ballast mass. A detailed finite-element track model for nonperiodic and asymmetrical mechanical defects was developed in [8]. The model takes into account the unsupported sleepers and the nonlinear multibody railroad vehicle system. The results are reported for different values of the forward velocities that show up to a 30% increase in the wheel–rail contact forces at higher speeds. In [9], the authors present a numerical model and experimental measurements of the dynamic loads on the ballast caused by trains passing a transition zone with hanging sleepers. The results show that the forces on the ballast vary significantly both in time and space on a transition, especially with the appearance of voids under the sleepers. A parametric study comprising nonlinear dynamic analyses using an FEM model of the track with sleeper voids is presented in [10]. Hanging sleepers were found to be strongly associated with critical situations of track degradation.
The performance assessment of a transition zone with unsupported sleepers by means of numerical analysis is shown in [11]. The stress redistribution towards the free ends of the void zones was analysed. A critical train speed was identified for the transition zone. In [12], the authors demonstrate the monitoring of distributed strain of rail during train passage over the bridge track with unsupported sleepers by applying a distributed optical fiber sensor. The distributed strain in the rail was measured within a length of 40.26 m and with a spatial resolution of 31.1 cm. The study could identify the location of the excessive strain due to an influence of unsupported sleepers on the girders of the bridge. In [13], the authors investigate the response of rails due to unsupported sleepers and insulated rail joints using an elastic–plastic FEM framework. The findings show the high sensitivity of plastic flow and rail material fatigue to the value of rail deflection.
Experimental investigation of the train-induced ground vibration at a test site with under-ballast plates is presented in [14]. Hammer excitations of the soil and the tracks, as well as train passages, indicated the presence of many voids between the sleepers and the ballast. A vehicle–track coupled dynamic model for heavy-haul freights with double suspension systems was built in [15], considering hanging sleepers. The results show that unsupported sleepers influence the aggravation of the wheel–rail interaction and affect the dynamic characteristics of the adjacent track structure with normal sleepers. The influence of the magnitude of the applied falling weight deflectometer (FWD) load on the measured track support stiffness was studied in [16].
The FWD tests were conducted on full-scale ballasted track models consisting of seven sleepers. It was shown that the track support stiffness measured by FWD is decreased due to the hanging sleepers. The effects of hanging sleepers and locally deteriorated substructures are investigated in [17]. Two numerical solutions were used for the simulation of track–substructure–ground response: the frequency-domain solution using a combination of beam elements for the track and an FEM model. The track vibrations were simulated and compared with other studies. The effects of the gap beneath the unsupported sleeper and the track support stiffness on increasing the sleeper displacement and track support force were studied in [18] using MBS and FEM numerical simulations. A series of regression equations were derived for the peak particle velocity in the surrounding environment of the railway track and the sleeper support stiffness for unsupported sleepers and fully supported ones.
The literature review presents a wide range of studies on numerical simulation of track and vehicle dynamic interaction considering unsupported sleepers. The numerical simulation is produced with help of models of different complexity, ranging from simple beam models to detailed 3D FEM ones.
3. Conclusions
The phenomenon of the intensive development of the unsupported sleeper zones has been known for a long time. However, the geometrical irregularity and wheel–track dynamic interaction are usually considered to be the reasons for the intensive settlement development. Most of the present theoretical studies, despite the complex models used, simply imitate the experimental measurements and do not consider the internal reasons for the dynamic interaction. The experimental studies usually do not analyse the dynamic impact in the ballast–sleeper contact.
The present experimental measurements and the simple numerical modelling of the dynamic interaction indicate the presence of the ballast impact even for low-velocity lightweight vehicles. Both results show that the impact occurs not directly under the wheel but before it with some time shift. Moreover, some minor dynamic interactions occur during the wheel leaving the void zone. Thereby, the wheel dynamic interaction is more than 50% lower than that of the sleeper. Thus, the main reason for the impact is the void closing.
The simulated loading patterns of the ballast present quite different processes for the different locations of the void zone. The loading in the impact location consists of the short impact, the following quasistatic part and the full unloading before the impact. On the other hand, the zones neighbouring to the void zone are characterised by a high pre-stress of the ballast and up to 2 times higher loading amplitudes compared to the track without void. The other zones in the void have low impact and a lower quasistatic load depending on the void sizes.
The study of void size influence on the dynamic interaction shows ambiguous relations. Different from a geometrical irregularity, the influence of the void depth on the dynamic interaction is such that the loadings increase until some depth and then should decrease until full unloading. Thus, the maximal impact values are present for some void depth.
The numerical simulation provides only an approximate imitation of the experimental measurement. It cannot explain the mechanism or the complex interrelations between the influencing factors and the impact loading. A simple analytical explanation is proposed by using the clamped beam as the basic model. The equation found for the sleeper impact velocity shows that it depends linearly on the train speed. It can explain why the low velocities cause high impacts. Thus, the dominating reason for the impact is not the wheel–track interaction but the rail quasistatic deflection rate. However, for high velocities, the resulting dynamic interaction could be a combination of both effects.
The DEM simulation of sleeper settlement under the main ballast loading patterns in the void zone shows almost no increase in the settlement intensity for the pre-stressed ballast despite the 30% increase in the maximal loadings. However, the impact loading case caused more than 8 times higher settlement intensity. The influence of the pre-stress and impact factors is the aim of further studies.
Thus, the phenomenon of settlement intensity increase for the case of impact loading has a relation to the property of the pressure distribution of the ballast layer and, first of all, the pressure breakdown zones under the sleeper ends. The growing zones can be explained by the reduction in the horizontal particle support of the ballast bed sides due to particle flow. The investigation of the further reason chain up to the root causes is the aim of further research.
References
- Grassie, S.L.; Cox, S.J. The Dynamic Response of Railway Track with Unsupported Sleepers. Proc. Inst. Mech. Eng. Part D Transp. Eng. 1985, 199, 123–136.
- Holtzendorff, K. Investigation of the Settlement Behaviour of Railway Ballast and the Void Forming on Railway Tracks. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2003.
- Lundqvist, A.; Dahlberg, T. Load impact on railway track due to unsupported sleepers. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2005, 219, 67–77.
- Bezin, Y.; Iwnicki, S.; Cavalletti, M.; De Vries, E.; Shahzad, F.; Evans, G. An investigation of sleeper voids using a flexible track model integrated with railway multi-body dynamics. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2009, 223, 597–607.
- Zhu, J.J.; Ahmed, A.K.; Rakheja, S.; Khajepour, A. Development of a vehicle–track model assembly and numerical method for simulation of wheel–rail dynamic interaction due to unsupported sleepers. Veh. Syst. Dyn. 2010, 48, 1535–1552.
- Kim, D.-S.; Kim, S.D.; Lee, J. Easy detection and dynamic behavior unsupported sleepers in high speed ballasted track. In Proceedings of the World Congress on Railway Research, Montreal, CA, Canada, 4–8 June 2006.
- Zhang, S.; Xiao, X.; Wen, Z.; Jin, X. Effect of unsupported sleepers on wheel/rail normal load. Soil Dyn. Earthq. Eng. 2008, 28, 662–673.
- Recuero, A.M.; Escalona, J.; A Shabana, A. Finite-element analysis of unsupported sleepers using three-dimensional wheel–rail contact formulation. Proc. Inst. Mech. Eng. Part K J. Multi-body Dyn. 2011, 225, 153–165.
- Varandas, J.N.; Hölscher, P.; Silva, M.A. Dynamic behaviour of railway tracks on transitions zones. Comput. Struct. 2011, 89, 1468–1479.
- Paixão, A.; Fortunato, E.; Calçada, R. The effect of differential settlements on the dynamic response of the train–track system: A numerical study. Eng. Struct. 2015, 88, 216–224.
- Coelho, B.Z.; A Hicks, M. Numerical analysis of railway transition zones in soft soil. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 230, 1601–1613.
- Yoon, H.-J.; Song, K.-Y.; Choi, C.; Na, H.-S.; Kim, J.-S. Real-Time Distributed Strain Monitoring of a Railway Bridge during Train Passage by Using a Distributed Optical Fiber Sensor Based on Brillouin Optical Correlation Domain Analysis. J. Sensors 2016, 2016, 1–10.
- Elsayed, H.; Lotfy, M.; Youssef, H.; Sobhy, H. Assessment of degradation of railroad rails: Finite element analysis of insulated joints and unsupported sleepers. J. Mech. Mater. Struct. 2019, 14, 429–448.
- Auersch, L. Tracks with under-ballast plates and their mitigation of train induced ground vibration. In Proceedings of the 24th International Congress on Sound and Vibration (ICSV 2017), Auburn, AL, USA, 23–27 July 2017.
- Zhang, D.; Wang, K.; Zhai, W.; Liu, P. Effect of unsupported sleepers on the wheel/rail dynamic interaction on heavy-haul railway lines. J. Vib. Shock 2017, 36, 1–7.
- Bayraktarova, K.; Eberhardsteiner, L.; Blab, R.; Tanigawa, H.; Nakamura, T.; Momoya, Y. Seasonal temperature distribution in rigid pavements. In Bearing Capacity of Roads, Railways and Airfields, Proceedings of the 10th International Conference on the Bearing Capacity of Roads, Railways and Airfields (BCRRA 2017), Athens, Greece, 28–30 June 2017; CRC Press: Boca Raton, FL, USA, 2017; pp. 2087–2093.
- Kaynia, A.M.; Park, J.; Norén-Cosgriff, K. Effect of track defects on vibration from high speed train. Procedia Eng. 2017, 199, 2681–2686.
- Mosayebi, S.-A.; Esmaeili, M.; Zakeri, J. Numerical investigation of the effects of unsupported railway sleepers on train-induced environmental vibrations. J. Low Freq. Noise, Vib. Act. Control. 2017, 36, 160–176.
More
Information
Subjects:
Engineering, Civil
Contributor
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
2.3K
Revision:
1 time
(View History)
Update Date:
19 Jul 2021
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No




