Key Issues in Hypersonic Propulsion

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Ingenito Antonella	+ 1684 word(s)	1684	2021-06-30 04:05:35	\|
2	format correction	Peter Tang	Meta information modification	1684	2021-07-01 04:55:01	\|

This entry is adapted from the peer-reviewed paper 10.3390/en14123690

This entry summarizes and discusses some critical aspects of flying hypersonically. The first is the L/D (lift over drag) ratio determining thrust and that in turn depends on the slenderness Küchemann’s τ parameter. This second parameter is found to depend on the relative importance of wave versus friction drag. Ultimately, all engineering drag is argued to depend on vorticity formed at the expense of the vehicle kinetic energy, thus requiring work by thrust.

scramjet engine hypersonic propulsion

1. Introduction

Hypersonic Propulsion is enjoying a revival of interest not seen since the 1960s, when the US Navy, USAF and the UK MoD were funding research and developments (R&D) in SCRJ engines. The reason is military applications that, using a current buzzword, have been defined ‘disruptive’, in that they may alter the strategic balance of power. Powered hypersonic missiles can potentially fly at M ~ 5–14 and altitude ~20–40 km where, because of the Earth curvature, they cannot be detected by radar until too late. Hypersonic gliders, after being boosted to much higher altitude (~10² km) fly to their destination unpowered. In both applications range may reach many thousands of km. They realize what E. Sänger ^[1] pursued until 1943 in Germany using rocket acceleration. Airbreathing engines as well as rocket boosting are the propulsion means.

1.1. Cruisers

The range, R, of cruisers is specified by the Bréguet formula ^[2], see Equation (2), derived from Newton’s Second Law when drag, D, is assumed equal to thrust T, and lift, L, equal to weight, W; the subscript in and fin in the weight W denote initial and final weight of the vehicle:

Isp tracks fuel consumption per unit thrust of the engine. Isp is the second parameter of importance of airbreathing engines. After acceleration to the cruising altitude the vehicle loses fuel mass at a nearly constant rate. Thrust determines the mass necessary to accomplish the mission via the specific fuel consumption (or Isp). Thrust is a function of L/D: as a first approximation, assuming L = W and T = D,

That is, the thrust necessary to the mission is equal to weight reduced by the (L/D) factor. This is an advantage compared to rocket propulsion where, to enable long range missions, thrust must be larger than weight. The ratio L/D is well known to be responsible for range: subsonic gliders may have L/D ~ 25–30 and airliners are close to 20. Allowance made for climbing and accelerating to the mission altitude, this relationship can be used to size the engine.

The L/D ratio is the most important parameter driving hypersonic flight range. Generally speaking, as speed increases past M = 1, the aerodynamic lift coefficient C_L diminishes while drag increases and, past M ~ 3, L/D drops rapidly: Figure 1 shows aerodynamic test data for the maximum L/D (as a function of the angle of attack) starting at M = 3, together with two theoretical curves developed by Küchemann ^[3]^[4]^[5] in the 1970s. Both are partially satisfactory, in the sense that the theoretical curves fit only parts of the data, and the data themselves are scattered. The flowfield determines L/D performance far more than the Mach number per se: such plots reveal the range of L/D potentially available, but their realization in a vehicle depends on actual lift and drag specific to the flow wrapped around and inside a vehicle shape.

Figure 1. L/D vs. flight Mach number.

Figure 1 shows that the L/D ratio is generally a decreasing function of Mach number, but actual values depend on specific L and D determined by the vehicle shape. The importance of L and D in determining thrust should spur initiatives to investigate the fundamental nature of both. Lift can be shown to be due to circulation (the Kutta–Jukowski theorem), and circulation is linked to vorticity; drag, however, is typically parceled among different contributions (form, friction, shock, induced) each dependent on different vehicle features. This paper recognizes the importance of the Küchemann parameter τ, the ratio between vehicle volume and (surface)^3/2 ^[6]. This ratio is in fact proportional to the ratio between shock drag and friction drag, and while still not accounting for fundamental drag physics, at least for a broad range of shapes supplies criteria to optimize hypersonic shapes.

The common factor to all contributions to drag is the formation of vorticity. A body moving in a still medium at supersonic speed must part the still air ahead. That is responsible for the formation of shocks and, in general, vorticity due to stagnation pressure non-uniformity. The simultaneous pressure and velocity field created by the body form vorticity as shown by the Crocco–Vaszonyi theorem in the compressible regime ^[7]. In terms of energy, inducing vorticity corresponds to rotationally accelerating the medium, and that requires work by the drag force resisting acceleration. All forms of drag end up by creating vorticity, which is eventually converted to heat by thermodynamic dissipation. Vorticity is formed by wall shear (wall friction), by shear and compression inside the thin shocks structure, and more generally by interaction between velocity and pressure field, as is the case of induced drag. Friction is a function of the vehicle surface area, and shocks depend on the volume being displaced by the vehicle, explaining why the Küchemann τ can help in increasing the L/D ratio.

Slender bodies are characterized by τ ~ 0.1, and waveriders (gliders) even a factor two less, precluding carrying much fuel or payload; their drag is mostly due to friction. At the other extreme are rocket powered vehicles that must store both fuel and oxidizer propellants and need τ ~ 0.2–0.3 or higher: their drag is mostly wave drag. The L/D ratio so important for range depends on the Küchemann τ and flight Mach number, M, as shown in the Figure 2. This figure can be interpreted as a sequence of L/D ratios as a function of Mach but also of shape (τ) for a class of vehicles characterized by a ‘pointy’ body (fuchsia-colored curves). The broken line corresponds to one of the theoretical Küchemann’s fit. Waveriders can maintain their relatively high L/D over a broad range of Mach numbers.

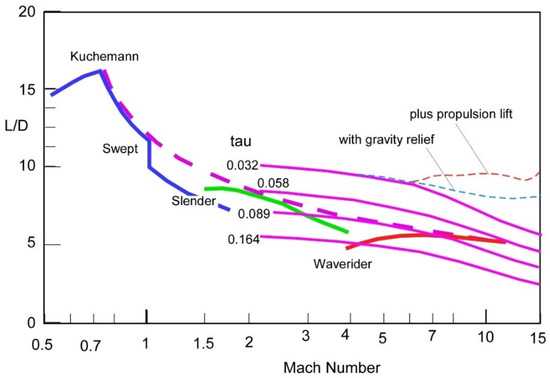
Figure 2. L/D vs. the flight Mach number and the shape factor τ (courtesy of P.A. Czysz).

Cruiser aerodynamics must ensure high L/D and high Isp in order to have thrust a small fraction of the take-off weight, and to limit the fuel fraction of take-off weight. Figure 2 enables preliminary engine and vehicle sizing. Realizing that drag is a function of vorticity simplifies conceptually the task of reducing it and suggests also ways, for instance at Mach numbers > 10, based on electromagnetics.

1.2. Accelerators

This class of applications includes first-stage airbreathing launchers and interceptors. Performance in terms of range and Isp is replaced by time-of-flight (=tof), and effective thrust, the difference (T-D), or (T-D)/T, determining acceleration. Short tof requires strong acceleration enabled by (T-D)/T ~ 1. Effective thrust determines the take-off, or launch, mass consisting mostly of fuel. The other performance quantity is the fuel fraction, m_fuel/m_TO, that has been calculated ^[3] as a function of T/D as

where total energy normalized using the fuel heat content is

The fuel energy Q should be the free energy F, but in Hunt’s analysis ^[8], it has been replaced by drag work DV. These are relationships enabling preliminary sizing of engine and vehicle for accelerator missions; they may also be used to calculate the fuel fraction for the climb and acceleration segment of cruisers.

2. Energy and Propulsion

Hypersonic flight depends on Isp and thrust, therefore, on L/D. This fact makes close engine-vehicle integration indispensable to reduce drag and weight. Integration, for instance, means that the air compression flowpath must also generate part of lift: the contraction ratio defining compression and temperature necessary to make the engine work is a function of forebody geometry and shape, both responsible for lift. A half-nozzle in 2-D geometries does the same. Together with these intertwined issues, a second critical issue is that of entropy.

Past M ~ 3 vehicle drag work increases and so does entropy, the third thermodynamic quantity of importance in hypersonics after kinetic energy (KE) and enthalpy ^[9]. Here the tacit assumption is that temperature and pressure limits of conventional ramjets can be overcome only with SCRJ engines or SCRJ-based combined engines. In fact, a hypersonic vehicle can be treated as a thermodynamic machine, its cycle including to a first approximation, the usual Brayton phases, and that is defined by in and out mass and energy fluxes of both air and fuel. Unlike subsonic or mildly supersonic vehicles, entropy becomes critically important in hypersonics, because it is strictly connected with vorticity and drag work ^[6]^[10]. Because the KE of the airstream, captured at great cost in terms of speed and drag, must not be wasted, the thickness of the entropy layer formed by the forebody curvature must be reduced as much as possible: thus, the vehicle should be ‘pointy’ or sharply spatular. By doing so, the volume of the bow and leading edges shock layers shrinks, streamlines are less ‘curvy’, and temperature and pressure gradients are moderate and entropy layers thinner. Entropy layers are sources of vorticity that causes drag and eventually dissipates and converts the KE of the airstream to useless heat. High temperature materials like ultra-high-temperature-ceramics are indispensable to design sharp leading edges and noses without resort to active cooling; past these high heat transfer zones (e.g., ~1 ft to ~1 m downstream), refractory metals and TBC may be adequate. Reducing entropy formation suggests using friction and shock heating to generate work or extra thrust: for instance, fuel used as a heat sink can produce KE and increase total thrust. In fact, thrust from high-speed fuel injection in the combustor becomes important past M ~ 10.

Much emphasis in hypersonic should be on conserving the KE of the airstream captured. Energy conservation and management are paramount when airstream KE may easily convert to enthalpy by friction and shocks ^[9]^[10]; means to recover internal and external heat fluxes are critical to enable vehicles to be re-usable: in this light cryogenic and endothermic fuels are very important, but logistics and cost must also be taken in consideration.

References

Sänger, E. Rocket Flight Engineering; National Aeronautics and Space Administration: Washington, DC, USA, 1965.
Bréguet, L. Calcul du poids de combustible consommé par un avion en vol ascendant. In Comptes Rendus Hebdomadaires des Séances de l’Académie des Sciences; Académie des Sciences: Paris, France, 1923; pp. 870–872.
Czysz, P.A.; Bruno, C.; Chudoba, B. Future Space Propulsion Systems and Integration; Springer/Praxis: Berlin/Heidelberg, Germany, 2018.
Ingenito, A.; Gulli, S.; Bruno, C.; Chudoba, B.; Czysz, P.A. Sizing of a fully integrated hypersonic commercial airliner. J. Aircr. 2011, 48, 2161–2164.
Ingenito, A. Subsonic Combustion Ramjet Design, SpringerBriefs in Applied Sciences and Technology; Springer: Cham, Switzerland, 2021.
Küchemann, D. The Aerodynamic Design of Aircraft; Pergamon Press: London, UK, 1978.
Bruno, C. Hypersonic Propulsion—An Introduction; Springer: New York, NY, USA, 2021; in press.
Hunt, J.L. Trade studies for hypersonic vehicles. In Proceedings of the 1st Joint Europe-US Short Course on Hypersonics, Paris, France, 7–11 December 1987.
Oswatitsch, K. Gas Dynamics; Academic Press: Cambridge, MA, USA, 1956.
Czysz, P.A.; Murthy, S.N.B. Energy management and vehicle synthesis. In Developments in High-Speed-Vehicle Propulsion Systems; Murthy, S.N.B., Curran, E.T., Eds.; AIAA: Reston, VA, USA, 1996; p. 587.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Energy & Fuels

Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Ingenito Antonella

View Times: 617

Update Date: 01 Jul 2021

Table of Contents

Video Upload Options

Confirm