Direct Ultrafast Laser Processing

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Ciro D'Amico	+ 5113 word(s)	5113	2021-06-16 08:14:34	\|
2	Format correct	Vicky Zhou	+ 5 word(s)	5118	2021-06-25 14:30:55	\|

This entry is adapted from the peer-reviewed paper 10.3390/photonics8060211

Direct ultrafast laser processing is nowadays considered the most flexible technique allowing to generate complex 3D optical functions in bulk glasses. The fact that the built-in optical element is embedded in the material brings several advantages in terms of prototype stability and lifetime, but equally in terms of complexity and number of possible applications, due to the 3D design. The generated optical functions, and in particular the single mode character of the light guiding element alongside the accessibility toward different spectral windows, depend on the refractive index contrast that can be achieved within the material transparency window and on the characteristic dimensions of the optical modification. In particular, the accessibility to the infrared and mid-infrared spectral domains, and to the relevant applications in sensing and imaging, requires increasing the cross-section of the guiding element in order to obtain the desired normalized frequency. Moreover, efficient signal extraction from the transported light requires nanometer size void-like index structures. All this demands a thorough knowledge and an optimal control of the material response within the interaction with the ultrafast laser pulse.

ultrafast lasers direct-laser-writing chalcogenide glasses integrated photonics linear and nonlinear optical functions.

1. Introduction

Bulk material refractive index engineering under exposure to focused ultrafast laser beams represents the fundament of direct-laser-writing (DLW) techniques ^[1]. The local change of the dielectric function induced by the laser due to energy absorption, and replicated via the laser/sample scan, is thus the building block of complex 3D embedded optical functions in transparent materials ^[2]^[3]. The technique consists in focusing the laser beam into the glass, usually by using high numerical aperture (NA) microscope objectives or optical lenses; the material is thus modified in correspondence of the focal region, where the intensity reached by the focused beam is sufficiently high that strong-field nonlinear ionization processes (multi-photon, tunnel, avalanche) are induced, with the subsequent generation of free carriers in the conduction band (electron-hole plasma). Part of the energy of the laser pulse is firstly transferred to the free carriers (inverse Bremsstrahlung) and subsequently to the material matrix (recombination of the plasma, electron–phonon coupling) due to collisional processes. The locally absorbed laser energy induces a local elevation of the temperature in the material, and eventually thermodynamic and hydrodynamic phenomena of matter modification and rearrangement can happen (phase transitions, material expansion and cavitation, cooling). Incubation effects are also important because point defects ^[4], broken chemical bonds, and, more generally, molecular rearrangement can be generated during the plasma recombination, which can be considered as precursors of the final permanent change obtained after many laser shots ^[5]^[6]. The permanent change is represented by a local modification of the glass refractive index, which can be either positive, corresponding to a local smooth densification (the so-called Type I index change) or negative, corresponding to a local rarefaction (the so-called Type II index change). In the case of smooth Type I index changes, by translating the sample during the irradiation process a structure can be generated capable to transport and guide light (a waveguide). In general, by using both Type I and Type II index changes, within a 3D optical design, complex optical functions can be defined ^[7]^[8]^[9]^[10]^[11], and sophisticated integrated photonic devices can be built, which can find applications in numerous domains, such as information technology, opto-fluidics, but also laser developments and quantum optics ^[12]^[13]^[14]^[15]^[16]. Possibilities of application further increase when one moves toward the infrared (IR) and mid-infrared (MIR) spectral regions, and they range from gas sensing for atmospheric and astronomical measurements (spectroscopy and interferometry) ^[8]^[17]^[18]^[19]^[20]^[21] to industrial monitoring/control processes.

The interest of DLW technique for building bulk embedded optical functions relies on a series of advantages with respect to existing micro/nano-technologies; this is not only related to intrinsic mechanical stability or optical performances of the embedded optical functions, but equally to the extension to 3D geometries, and the high flexibility in designing index properties, relevant scales, and therefore modal features. The extension to the third dimension in compact geometries allows for example addressing the complexity of the next generation of astronomical instruments (especially for multi object spectroscopy and stellar interferometry) ^[20]^[21] due to the embedded nature of the technology. Basic optical functions, as for example light transport, wavefront filtering, beam splitting and combination, and signal information extraction, can be integrated within a monolithic compact photonic device, contributing to the development of complex, compact integrated instruments for astronomy signal collection and processing. As an example, the spectral domains of 3–5 µm and 8–12 µm are of great astrophysical interest as numerous molecular organic tracers (water, CO₂, ozone) can be sensed at these wavelengths, and this can be applied to the research of life on exoplanets.

Concerning the optical bulk materials, the question of accessibility and fabrication requirements in the MIR region puts forward chalcogenide glasses (ChGs) as a promising solution. ChGs are an important class of amorphous semiconductors, which finds applications in many fields, as for example phase-change memories, solar cells, sensors, and photonics ^[22]^[23]^[24]^[25]^[26]^[27]. Their name is due to the fact that they contain one or more chalcogen elements from group 6a of the periodic table (sulphur, selenium, and tellurium), which are covalently bonded to network formers such as As, Ge, Sb, Ga, Si, or P. This gives a very broad range of possible glass-forming systems, generating glasses with a large variety of optical properties, such as nonlinearity, photosensitivity, and infrared transparency ^[28]^[29]^[30]^[31]^[32]^[33]. The energy band-gap of these material is lowered by the fact that their inter-atomic bonds are weak if compared to those in oxide glasses. Moreover, the vibrational energies of the bonds are low because the constituent atoms are particularly heavy. This gives them a large transparency up to the mid-infrared, and the heavier the constituent atoms the larger the transparency window. Typically, Sulphur-based ChGs transmit to about 11 μm, selenium-based ChGs to about 15 μm, and tellurium-based ChGs to beyond 20 μm. However, physical properties such as the glass transition temperature (T_g), glass hardness and strength generally deteriorate with weaker bonding and therefore decrease with long-wave transparency. On the contrary the nonlinear index (200 to 1000 times higher than in fused silica) generally increases with weaker bonding and lower band-gap.

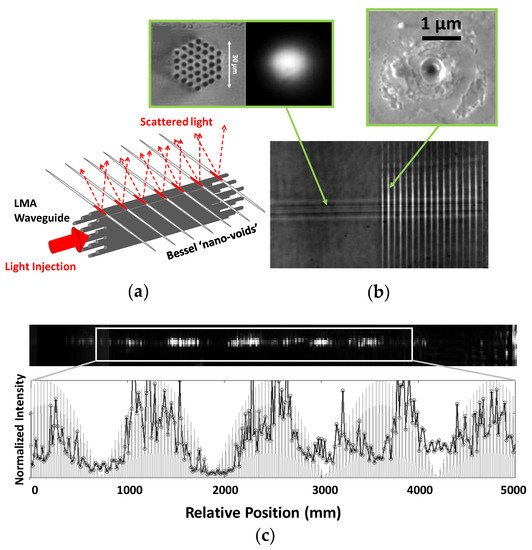
2. Response of Sulfur-based ChG Glasses to Ultrafast Lasers

The final result of the laser-induced local index change in ChGs strongly depends on their elemental composition and their thermal history. The role played by the glass elemental composition is evidenced by comparing the optical response of two ChGs, namely As₂S₃ and Ge₁₅As₁₅S₇₀, under femtosecond laser irradiation. Typical photo-inscribed longitudinal waveguides, obtained by translating the sample in the confocal direction during laser irradiation, are shown in Figure 1a (As₂S₃) and Figure 1b (Ge₁₅As₁₅S₇₀). The irradiation conditions were the same for the two glasses, with a laser energy density (in vacuum) at the center of the focal region reaching about 130 J/cm³. As can be clearly seen, As₂S₃ and Ge₁₅As₁₅S₇₀ samples show an almost opposite response, which can be summarized as follows: (1) As₂S₃ presents mainly negative refractive index modifications; positive index Type I modifications are observed for very low laser doses in a relatively narrow range and with a very poor contrast; (2) Ge₁₅As₁₅S₇₀ presents mainly positive index modifications over a wide range of laser dose values (negative modifications are observed, but only at relatively high laser doses). A first conclusion can therefore be given: doping with Ge an As-S glass structure, having very narrow windows for positive index modifications, allows creating glasses (Ge-As-S structures) with a large window for positive index changes, which are much more suitable for photonic applications. A first remark can be done concerning the role of Ge insertion: the quasi planar As-S molecular structure acquires a 3D connectivity after inserting Ge, as depicted in Figure 1c; one can claim therefore that this is a key factor to increase the level of structural flexibility.

On the other side, several levels of structural arrangements and rigidity of the glass matrix can be obtained depending on the thermal history during glass preparation. The glass thermal history is a key factor in establishing the link between the matrix connectivity and the degree of photo-induced densification. The process by which Ge-As-S glasses are prepared generates quite unrelaxed glasses with characteristic volumes higher than the volume corresponding to a relaxed configuration, and therefore a lower density. Re-annealing should enable a structural relaxation process that corresponds closely to a structural equilibrium at the annealing temperature, little affected by the cooling tie as the relaxation times becomes prohibitively long ^[34]. In other words, from a standard normal thermodynamic behavior of a chalcogenide glass, the longer the annealing time at temperatures under T_g, the lower its final volume, i.e., the higher its density ^[35], as schematized in Figure 1e. The glass refractive index, which depends on its density, will depend therefore on its thermal history. A glass annealed for a long time at a temperature close to T_g will have therefore a higher refractive index than a glass annealed for a short time; global refractive index variations of the order of 10⁻⁴ to 10⁻³ can be achieved by annealing ^[36]^[37]. The enthalpy represents a first evaluation of structural flexibility allowing evaluating the strength of additional laser-induced modification on a structure with different degrees of relaxation, up to the point where, in principle, no further structural changes and relaxation can be induced. In re-annealed samples, where the glass structure is relaxed, it should be much harder to induce photo-contraction, and furthermore the opposite effect of photo-expansion should be observed, especially at higher intensities ^[38]. To verify this point, ultrafast laser photo-inscription of Type I waveguides has been performed in two samples, a reference Ge₁₅As₁₅S₇₀ glass, as prepared in the laboratory with a standard procedure, and a similar sample but re-annealed during 72 h at T_g–15 °C and then slowly cooled to room temperature. The photo-inscription process was performed in both samples under the same experimental conditions and the response of the two samples was evaluated by performing guiding tests (injecting light in the waveguides and evaluating the intensity of the near-field guided modes at the exit). The results are shown in Figure 1d,e, the response of the reference and re-annealed samples was significantly different. The reference sample (top) showed the expected response, a good photo-induced local densification and a good confined guided mode, while waveguides photo-inscribed in the re-annealed sample (bottom) showed a much lower index contrast with a poor guided mode. Furthermore, as can be seen on the bottom of Figure 1d, in the re-annealed sample, the region where the laser pulse is more intense (the center of the pulse) gives an inverted response, with a negative refractive index variation. This behavior was expected and it is in good agreement with the results reported in ^[38], i.e., irradiating the surface of high enthalpy chalcogenide glass with low intensity laser pulses results in a large photo-contraction, while high intensity irradiation can generate the exactly opposed effect, i.e., photo-expansion, in low enthalpy samples. These results can be explained in terms of volume reduction by structural relaxation when high enthalpy ChGs samples are annealed for a long time slightly under T_g.

Raman shift analysis performed on non-irradiated and irradiated Ge₁₅As₁₅S₇₀ samples showed many molecular structural changes corresponding to the irradiated region, some of which are a clear signature of an augmented disorder under laser irradiation, and a possible cause of photo-induced densification. Measurements on re-annealed samples showed the same molecular changes after laser exposure, but less intense than in the case of non-reannealed samples, in agreement with the difference observed in the refractive index change. Recently, Gretzinger et al. ^[39] reported on structural rearrangements and ion migration in correspondence of Type I structures photowritten in GLS, as evidenced by Raman spectroscopy.

Based on all the results presented above, the following scenario has been proposed. First, the insertion of Ge in a quasi-planar As-S matrix introduces a 3D connectivity and new degrees of freedom, allowing for higher structural flexibly and so a higher relaxation potential. This indicates that the laser role is to trigger locally states with a different degree of relaxation with respect to the pristine sample, inducing further relaxation in unrelaxed or partially relaxed matrices (with a result in index increase) or to induce structural constraints in relaxed matrices up to thermomechanical effects (local expansion). The question is then how the laser pulse is able, via the deposited energy, to trigger molecular mobility and structural rearrangement ^[40]. As a consequence of the ionization of the sample by the focused laser pulse, a number of electrons are promoted from the valence band to the conduction band by two-photon absorption. When electrons are excited to the conduction band, covalent bonds of the glass matrix are weakened and molecular mobility is allowed even at room temperatures where normally it is prohibited by slow kinetics. The lifetime of the electron plasma generated by a single pulse (which can reach few tens of nanoseconds ^[41]) is too short to induce an efficient molecular mobility with only one laser pulse; however, following laser pulse after laser pulse, a relaxation channel is generated through which the glass structure is allowed to rearrange even at room temperature. The irradiation process can be seen therefore as a way to remove the kinetic constraint to the thermodynamically driven relaxation. These results are in good agreement with previous works reported in the literature. Hisakuni and Tanaka ^[34]^[42] reported on photo-induced glass softening effect in amorphous As₂S₃. They have shown the possibility of a-thermally photo-induced fluidity, i.e., the possibility of introducing degrees of freedom and structural mobility via paths that are not exactly temperature driven in the glass matrix under laser irradiation. More recently, Lucas and King ^[40] reported on the observation of fast light-activated relaxation in GeSe₉ chalcogenide glass illuminated with sub-band-gap light from a Ti:Sapphire laser.

Figure 1. Comparison of the refractive index change results (PCM) of the waveguide laser photo-inscription process in (a) As₂S₃ and (b) Ge₁₅As₁₅S₇₀ glasses with the same laser parameters (2 mW (@100 kHz) and 160 fs duration) and for two different scanning speeds. The translation speeds of the samples are indicated on the images; (c) A quasi planar As-S molecular structure acquires a 3D connectivity (Ge-As-S) after doping with Ge, increasing its structural flexibility; (d,e) Comparison of the index change results (PCM) of the waveguide photo-inscription process in a pristine (top) and longtime re-annealed (bottom) Ge₁₅As₁₅S₇₀ samples by 2 mW (@100 kHz) and 160 fs laser pulses, with two different scanning speeds. The translation speeds are indicated on the top; (f) Schematic of the thermal history of annealed chalcogenide glasses and its influence on the enthalpy of the microscopic glass structure.

3. Infrared Light Transport by Embedded Large Diameter Waveguides

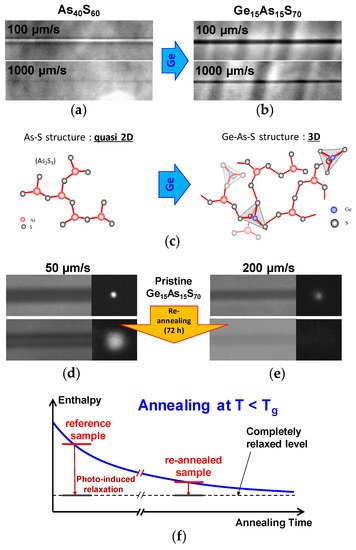
The requirements of single mode guiding in the MIR domain impose constraints on minimal waveguide section diameters (with ranges in the tens of µm) and index contrast (approaching or exceeding 10⁻³). In response to these limitations mainly two approaches have been tested, namely the slit-shaping method ^[43]^[44] and the evanescently coupled multicore waveguide bundle design ^[7]^[9]. In standard irradiation conditions, laser photo-inscribed waveguides have transverse cross-sections with few micrometers in diameter, and, particularly for transverse scan schemes, the cross-section is asymmetric and elongated in the direction of the confocal axis. One of the most effective spatial shaping techniques by which one can obtain either a higher symmetry of the transverse profile (increasing the circularity of the guided mode and reducing polarization sensitivity) or a larger cross-section diameter is the slit-shaping technique, allowing to change the profile along the propagation axis and thus the confocal volume. The technique has been introduced by Cheng et al. ^[43] using partial beam truncation along one transverse direction, and then reinforced via astigmatic control by Osellame et al. ^[44]. As a consequence of Gaussian beam propagation laws, decreasing the initial beam waist along one transverse direction leads to the related increase of the corresponding focal waist in the focal plane up to the point where it becomes comparable to the confocal length. A quasi-circular symmetry thus can be obtained in the form of a disk that can be replicated by transverse scanning to form a waveguide of larger diameter and circular cross-section.

Further flexibility in the normalized frequency requires increasing even more the waveguide cross-section diameter, beyond the typical limit of the slit-shaping technique (tipically 10-15 µm). The flexibility in designing optical functions in a waveguide array concept is considerable, ranging from photonic crystal fibers to imaging devices, routers, and mode convertors ^[45]^[46]^[47]. In the context of LMA light transport, evanescently coupled fibers ^[48] or embedded waveguides ^[43] were demonstrated to be potential efficient solutions. The coupling efficiency in waveguide arrays is the key engineering factor in designing the properties of the array, and it can straightforwardly be designed using index contrast, inter-trace spacings, or lengths for various spectral domains. In terms of optical guiding, based on a multicore fiber concept, a matrix of waveguides permits upon central injection and gradual coupling in the next neighboring waveguides the development of in-phase modes that will coherently overlap, thus forming a large-area single mode covering the whole array. An example of photo-inscribed multicore array waveguides functioning in single-mode operation is given in Figure 2c. Typical hexagonal arrangements with 37 micron-spaced 10 mm-long traces were used in a Ge₁₅As₁₅S₇₀ sample. For typical single trace NA below 0.05, equivalent to index contrasts of up to 5 × 10⁻⁴ at 800 nm, the individual modes superpose coherently and create super-single-mode propagation over the bundle cross-section. Higher NA and/or section diameters lead to stronger mode localization and favorable conditions for multimode guiding. The mode becomes more confined when increasing the index contrasts and keeping the diameter constant, or inversely can be extended with larger inter-trace separation and keeping the index contrast constant. Consequently, the single trace NA can be adjusted for single mode conditions, with losses around 1 dB/cm. Even larger sections (up to 100 µm or more) with multimode character can be obtained using multicore bundles with slit-shaped individual traces.

Tests of MIR light guiding with multicore and slit-shaped structures with index contrasts up or in excess of 10⁻³ are given in Figure 2. The results indicate high transmittance over the whole black body source range (2–13 µm) convoluted with the glass transparency window (0.5–11 µm) and the detector response (FLIR camera). The large band response in Figure 2a shows chromatic effects with apparent slightly higher attenuation at large wavelengths depending on the degree of mode confinement, obtained by increasing the waveguide index contrast. The chromaticity of the structures can be controlled via index contrast engineering. Chromatic effects are less apparent in slit-shaped traces (Figure 2b), with main index contrast effects in the overall guide transparency. Spatial mode profiles under coherent light injection were tested at 3.39 µm He-Ne laser radiations for multicore structures and show symmetric single mode guiding (Figure 2d) with mode areas matching the size of the multicore structure in Figure 2c. The result is confirmed by numerical simulations ^[9]. An example of a calculated mode is given in Figure 2e for a hexagonal structure having the same characteristic of the experimental one. The guiding performances were experimentally analyzed via the cut-back method on multicore guides of several lengths, indicating propagation losses in the 1 dB/cm range at 3.39 µm injection. More recently, Masselin et al. ^[49] showed that propagation losses as low as 0.11 dB/cm at 1.5 µm can be obtained by optimizing the index contrast of multicore structures in bulk ChGs. Other techniques and configurations have been proposed in the literature in order to increase the guiding cross-section area. These techniques are mainly based on depressed cladding concepts ^[16]^[50]^[51] (photo-inscription of a low index Type II cladding surrounding the guiding area), or on a 1D version of the multicore concept ^[52] (periodic arrangement of Type I index slabs). In particular, depressed-cladding techniques can be effective in bulk materials which cannot sustain contrasted Type I index structures, as is the case for example in As₂S₃ chalcogenide glass, as will be discussed below.

Figure 2. (a) MIR large band guiding in a multicore waveguide. The spectral dependencies of the laser-induced structures as a function of the index contrast is also shown. Two input powers at 2 and 6 mW are used with the same sample scan velocities of 0.1 mm/s, in order to obtain two different index contrasts. Higher contrast leads to better guiding in the large wavelength spectral domain; (b) Laser energy dose dependent spectral behavior of slit-shaped traces via two scan velocities (0.1 and 0.2 mm/s) at the same input power of 380 mW. Higher contrast leads to better guide transparency; however, overall performances lay below those of the multicore; (c) Multicore structure written in bulk Ge₁₅As₁₅S₇₀ glass (10 mm length) at 2.4 mW, 100 kHz input laser conditions via a NA 0.5 aspherical lens at 0.5 mm/s scan speed. The inter-trace spacing is 5 µm, and the whole diameter 30 µm; (d) The corresponding single mode guided at 3.39 µm, detected via a FLIR camera ^[9]; (e) Finite element analysis for a guided mode at 3.39 µm in a multicore hexagonal structure with 5 µm spaced, 4 µm thick individual traces of NA = 0.08.

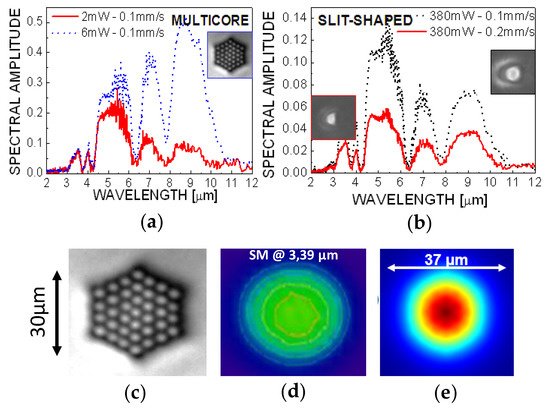
4. Signal Extraction by Embedded High-Aspect-Ratio Bessel Nanovoids

Reducing the size and power consumption of detecting instruments has always been an issue for spatial astronomical applications. Nowadays, with the development of Nanosat projects, the possibility of achieving very high resolution in a very compact and light device gives waveguide optics a very broad field of application. A possible approach is to develop integrated spectrometers where the spectrum is obtained by Fourier Transform of a static interferogram, as proposed in the SWIFTS-Lippmann configuration ^[53]^[54]. In the present approach, the stationary wave is obtained by superposing the direct and backward guided modes of a simple channel optical waveguide, the latter being obtained without using a mirror but only Fresnel reflection at the waveguide output, exploiting the high refractive index of GLS waveguides. For sampling the stationary wave inside the waveguide, periodic nanodots of gold sputtered on the surface ^[55], or grooves obtained by Focused Ion Beam technology (FIB) ^[54], are typically utilized. For the first time, the classical nano-scattering centers, fabricated by time-consuming lithographic techniques, are here replaced by Bessel high aspect-ratio nanovoids photo-written by DLW perpendicularly to the waveguide ^[10] (the energy scattered by the periodic nanostructure, which is then used to sample the signal transported in the waveguide), as shown in Figure 3a,b. Periodic Bessel nanovoids with a transverse section below 500 nm (see the inset on top-right of Figure 3b) and an axial dimension above 150 µm, separated by 10 µm were employed. As a guiding element, a photo-inscribed LMA waveguide was used, in order to achieve large diameter mode guiding in the NIR and MIR with single mode characteristics. This was based on a centered hexagonal arrangement of 37 parallel waveguides A view on the multicore waveguide cross-section structure and the corresponding guided mode at 1550 nm, with a diameter of about 20 µm, is shown in the top-left inset of Figure 3b. The trial was performed in GLS. The main interest of this technology is not only that the waveguide cross-section diameter and index can be adjusted in order to have single mode guiding at the desired wavelength, but also that the sampling nano-voids can be written in a very short time using DLW (few minutes) over the whole length of the sample (typically few cm, and this is highly suited in order to increase the spectral resolution), whereas classical techniques such as FIB or lithography take hours, and are limited to small lengths (typically 500 μm), requiring mask shifting in order to cover high areas. Moreover, the sampling nano-voids can be set at different depths in order to optimize interaction with the evanescent field of the waveguide, optimizing therefore the scattered signal, and finally their form factor can be easily changed, in order to modify the extraction efficiency and directivity ^[56]. This is a perfect demonstration of the high flexibility of the DLW technique in realizing compact embedded detectors, if compared to existing industrially mature lithographic techniques.

Figure 3. (a) Schematic concept of LMA light transport and signal extraction optical functions, obtained by using multicore array waveguide concept (for guiding) and high aspect ratio Bessel nano-voids photo-written transversally to the waveguide (signal extraction by scattering); (b) Top-view of the prototype schematized in (a) fabricated in bulk GLS glass. The inset on the left shows the multicore cross-section of the fabricated LMA waveguide and the corresponding guided mode obtained by injecting the waveguide with a 1550 nm SLED. The inset on the right shows the cross-section of the single Bessel nano-void structure; (c) Sampling of the λ = 3.39 µm signal confined in the waveguide and extracted from the periodic Bessel nano-voids (input injection on the left, output interface on the right). Although the signal is under-sampled (discussion in the text), a stationary wave is clearly visible as formed in the waveguide by interference.

5. Photoinscription of 3D Nonlinear Optical Functions in Bulk ChG Glasses

Designing bulk 3D optical functions with additional Kerr nonlinearity becomes possible in ChGs, due to their high nonlinear index, enabling the development of all-optical signal processing concepts based on the excitation of spatial and temporal solitons at relatively low peak powers ^[45]^[57]. In this context, evanescently coupled two-dimensional waveguide arrays with a third-order nonlinear response have been proposed for light manipulation due to the strong sensitivity to injected power and subsequent discrete coupling ^[58]^[59]^[60]^[61]. A good example in this sense is represented by the function of a passive saturable absorber with a variable modulation depth ^[62] relying on discrete nonlinear localization of light in arrays of coupled waveguides ^[58]. The nonlinear waveguide arrays geometry is particularly interesting as the fabrication procedure can be extended to 3D embedded designs in ChG glasses using the ultrafast DLW technique. The design of such an optical device in bulk glasses implies the photo-inscription of Type I waveguide in longitudinal configuration and in a centered hexagonal arrangement, where the maximum transfer from the central to the side waveguides can reach up to 86% ^[63], controllable via the length and the index contrast of the surrounding waveguides. In the present case, the Type I central waveguide has a length of 9.1 mm, with the surrounding hexagon at a length of 2.4 mm. Details about the irradiation conditions can be found in ref. ^[64].

Type I positive index waveguides with typical index contrasts in the range of 10⁻⁴−10⁻³ were generated. A summary of the optical performance of the device, with its conceptual design, is shown in Figure 4a. Upon core injection with ps-long pulsed laser at 800 nm, the collective optical response of the waveguide array shows a strong intensity dependence, with the low-power propagating field being redistributed between the central core and the surrounding waveguides due to evanescent coupling, and high-power favoring decoupling and core propagation. Figure 4b indicates the measured low-power (around 0.2 kW) repartition of energy in the structure, with a minimal amount localized in the core. Increasing the intensity, the Kerr contribution increases the effective index of the central waveguide and the light becomes self-localized (Figure 4c), achieving more than 90% transmission in a stable manner. The power-dependent field propagation in the core suggests its potential as a saturable absorber. We noted that femtosecond injection leads to output transmission fluctuations, due to pulse spatial and temporal nonlinear distortions during propagation in the array. The spatiotemporal propagation of the pulses in the micro-structured GLS sample has been modeled by means of a discrete–continuous version of the UMEs ^[57], as described in detail in ref. ^[64]. The results for simulation concerning the picosecond input case are given in Figure 4d. This presents the fluence profile at the output of the saturable absorber for two levels of input pulse intensity. The modal profiles are comparable to the experimental profiles shown in Figure 4b,c, which were taken under similar input conditions. The overall transmission response of the saturable absorber (with respect to the performance of a single waveguide) is summarized in Figure 4e, which displays the experimental transmission data in the central core as a function of the estimated peak intensity of the injected pulse. The analogous results of the simulation are shown in the same graph (calculated assuming all the energy of the pulse is coupled in the waveguide), indicating good agreement between experiment and theory.

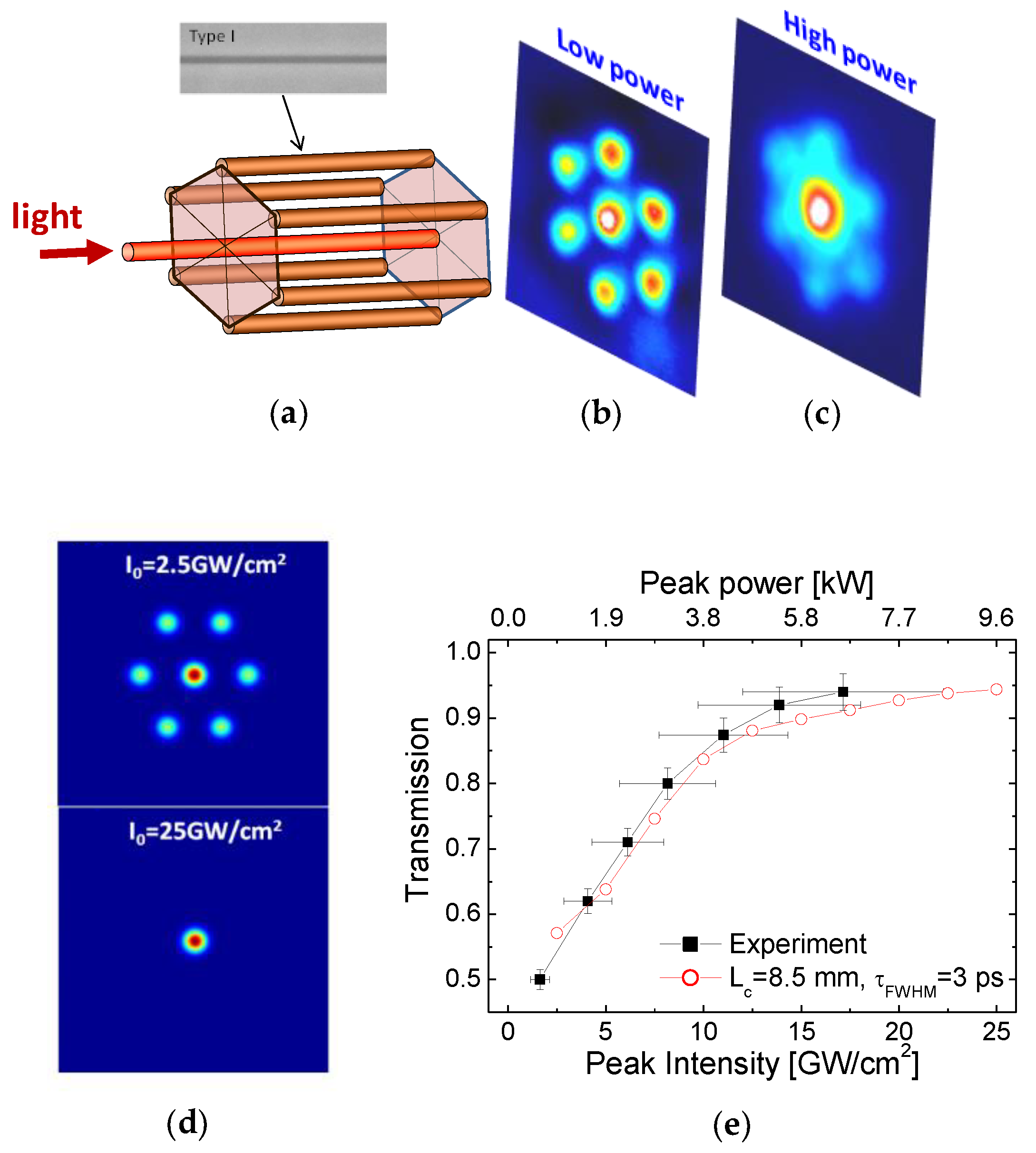Figure 4. (a) Conceptual design of the centered hexagonal array with a 9.1 mm length for the core guide and a 2.4 mm length for the surrounding hexagon. The inter-trace spacing is 13 μm; (b) Output mode in the case of low-power (0.2 kW) injection with a uniform spread of energy; (c) Output mode in the case of high-power (7 kW) injection with a core localization of light. The injected pulse duration (FWHM) is 3 ps; (d) Output mode snapshots resulting from the simulation of the propagation in the photonic saturable absorber of a λ = 800 nm positively chirped pulse of 3 ps, for an input pulse intensity of 2.5 GW/cm² (top) and 25 GW/cm² (bottom); (e) Intensity and power-dependent transmission in the hexagonal array. Experimental values (solid squares) and simulation data (open circles) are plotted. The x-error bars reflect the precision in evaluating the intensity via the accuracy of mode size estimations.

6. Conclusions

In conclusion, ultrafast photo-inscription concepts for designing laser-written waveguides in sulfur-based chalcogenide glasses have been explored, which are compatible with light transport in the infrared and mid-infrared spectral domains. They emphasize a correlation between irradiation design and material engineering. The focal slit-shaping technique and evanescently-coupled and structured multicore waveguides are efficient solutions for large-mode-area guiding in the infrared ranges. The study of the response to ultrafast lasers showed how Ge-doping an As-S chalcogenide structure increases the structural flexibility of S-based chalcogenide glasses, allowing for a larger processing window of positive index changes, via photo-induced local contraction. Equally, it has been shown how the thermal history of the sample can influence its structural flexibility, a short annealing time under T_g corresponding to a reduced packaging, allowing for a more efficient response.

From an applicative point of view, it has been demonstrated how using multiscale laser processing, from micron-sized large-mode-area waveguides traces to nanoscale one-dimensional Bessel scatterers, it is possible to obtain compact high spectral and spatial resolution spectrometer designs, embedded in the bulk of chalcogenide glasses and working in the infrared domain. By direct laser photo-inscription, it is possible to design the modal characteristics, such as waveguide refractive index, as well as the length of the diffraction nanovoids grating, so that the spectral resolution and the spectral bandwidth can be easily tuned, giving to these photowritten embedded photonic prototype a very high flexibility. The obtained results, although preliminary and to be optimized, are encouraging for lightweight applications, such as drone and cubesat interferometry projects, where we expect this type of compact spectro-interferometers to be a good tradeoff between performances and fabrication time and cost. Finally, by exploiting the high nonlinearity of chalcogenide glasses (GLS in the present case), nonlinear embedded optical functions can be also defined. In particular, a near-infrared saturable absorber 3D concept based on ultrafast laser-fabricated coupled waveguide arrays has been demonstrated, which is suitable for infrared ultrashort laser pulses at a low, kilowatt threshold.

References

Davis, K.M.; Miura, K.; Sugimoto, N.; Hirao, K. Writing waveguides in glass with a femtosecond laser. Opt. Lett. 1996, 21, 1729–1731.
Itoh, K.; Watanabe, W.; Nolte, S.; Schaffer, C. Ultrafast processes for bulk modification of transparent materials. MRS Bull. 2006, 31, 620–625.
Nolte, S.; Will, M.; Burghoff, J.; Tünnermann, A. Femtosecond waveguide writing: A new avenue to three-dimensional integrated optics. Appl. Phys. A Mater. Sci. Process. 2003, 77, 109–111.
Pacchioni, G.; Skuja, L.; Griscom, D.L. Defects in SiO2 and Related Dielectrics: Science and Technology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000.
Mishchik, K.; D’Amico, C.; Velpula, P.K.; Mauclair, C.; Ouerdane, Y.; Boukenter, A.; Stoian, R. Ultrafast laser-induced electronic and structural modifications in bulk fused silica. J. Appl. Phys. 2013, 114, 133502.
Masselin, P.; Le Coq, D.; Cuisset, A.; Bychkov, E. Spatially resolved Raman analysis of laser induced refractive index variation in chalcogenide glass. Opt. Mater. Express 2012, 2, 1768–1775.
Cheng, G.; D’Amico, C.; Liu, X.; Stoian, R. Large mode area waveguides with polarization functions by volume ultrafast laser photoinscription of fused silica. Opt. Lett. 2013, 38, 1924–1926.
Thomson, R.R.; Birks, T.A.; Leon-Saval, S.G.; Kar, A.K.; Bland-Hawthorn, J. Ultrafast laser inscription of an integrated photonic lantern. Opt. Express 2011, 19, 5698–5705.
D’Amico, C.; Cheng, G.; Mauclair, C.; Troles, J.; Calvez, L.; Nazabal, V.; Caillaud, C.; Martin, G.; Arezki, B.; LeCoarer, E.; et al. Large-mode-area infrared guiding in ultrafast laser written waveguides in sulfur-based chalcogenide glasses. Opt. Express 2014, 22, 13091–14001.
Martin, G.; Bhuyan, M.; Troles, J.; D’Amico, C.; Stoian, R.; Le Coarer, E. Near infrared spectro-interferometer using femtosecond laser written GLS embedded waveguides and nano-scatterers. Opt. Express 2017, 25, 8386–8397.
Cvetojevic, N.; Jovanovic, N.; Gross, S.; Norris, B.; Spaleniak, I.; Schwab, C.; Withford, M.J.; Ireland, M.; Tuthill, P.; Guyon, O.; et al. Modal noise in an integrated photonic lantern fed diffraction-limited spectrograph. Opt. Express 2017, 25, 25546–25565.
Watanabe, W.; Kuroda, D.; Itoh, K.; Nishii, J. Fabrication of Fresnel zone plate embedded in silica glass by femtosecond laser pulses. Opt. Express 2002, 10, 978–983.
Monat, C.; Domachuk, P.; Eggleton, B.J. Integrated optofluidics: A new river of light. Nat. Photonics 2007, 1, 106–114.
Marshall, G.D.; Dekker, P.; Ams, M.; Piper, J.A.; Withford, M.J. Directly written monolithic waveguide laser incorporating a distributed feedback waveguide-Bragg grating. Opt. Lett. 2008, 33, 956–958.
Sansoni, L.; Sciarrino, F.; Vallone, G.; Mataloni, P.; Crespi, A.; Ramponi, R.; Osellame, R. Polarization Entangled State Measurement on a Chip. Phys. Rev. Lett. 2010, 105, 200503.
Caulier, O.; LeCoq, D.; Bychkov, E.; Masselin, P. Direct laser writing of buried waveguide in As2S3 glass using a helical sample translation. Opt. Lett. 2013, 38, 4212–4215.
Bland-Hawthorn, J.; Kern, P. Astrophotonics: A new era for astronomical instruments. Opt. Express 2009, 17, 1880–1884.
Ta’eed, V.G.; Baker, N.J.; Fu, L.; Finsterbusch, K.; Lamont, M.R.E.; Moss, D.J.; Nguyen, H.C.; Eggleton, B.J.; Choi, D.Y.; Madden, S.; et al. Ultrafast all-optical chalcogenide glass photonic circuits. Opt. Express 2007, 15, 9205–9221.
Thomson, R.R.; Kar, A.K.; Allington-Smith, J. Ultrafast laser inscription: An enabling technology for astrophotonics. Opt. Express 2009, 17, 1963–1969.
Jovanovic, N.; Tuthill, P.G.; Norris, B.; Gross, S.; Stewart, P.; Charles, N.; Lacour, S.; Ams, M.; Lawrence, J.S.; Lehmann, A.; et al. Starlight demonstration of the Dragonfly instrument: An integrated photonic pupil-remapping interferometer for high-contrast imaging. Mon. Not. R. Astron. Soc. 2012, 427, 806–815.
Cvetojevic, N.; Norris, B.R.M.; Gross, S.; Jovanovic, N.; Arriola, A.; Lacour, S.; Kotani, T.; Lawrence, J.S.; Withford, M.J.; Tuthill, P. Building hybridized 28-baseline pupil-remapping photonic interferometers for future high-resolution imaging. Appl. Opt. 2021, 60, D33–D42.
Eggleton, B.; Luther-Davies, B.; Richardson, K. Chalcogenide photonics. Nat. Photonics 2011, 5, 141–148.
Hu, J.; Meyer, J.; Richardson, K.; Shah, L. Feature issue introduction: Mid-IR photonic materials. Opt. Mater. Express 2013, 3, 1571–1575.
Sanghera, J.S.; Aggarwal, I.D. Active and passive chalcogenide glass optical fibers for IR applications: A review. J. Non Cryst. Solids 2008, 256–257, 462–467.
Gai, X.; Han, T.; Prasad, A.; Madden, S.; Choi, D.-Y.; Wang, R.; Bulla, D.; Luther-Davies, B. Progress in optical waveguides fabricated from chalcogenide glasses. Opt. Express 2010, 18, 26635–26646.
Labadie, L.; Martin, G.; Anheier, N.C.; Arezki, B.; Qiao, H.A.; Bernacki, B.; Kern, P. First fringes with an integrated-optics beam combiner at 10µm. A new step towards instrument miniaturization for mid-infrared interferometry. Astron. Astrophys. 2011, 531, A48–A54.
Vázquez, M.R.; Sotillo, B.; Rampini, S.; Bharadwaj, V.; Gholipour, B.; Fernández, P.; Ramponi, R.; Soci, C.; Eaton, S.M. Femtosecond laser inscription of nonlinear photonic circuits in Gallium Lanthanum Sulphide glass. J. Phys. Photonics 2019, 1, 015006.
Kanbara, H.; Fujiwara, S.; Tanaka, K.; Nasu, H.; Hirao, K. Third-order nonlinear optical properties of chalcogenide glasses. Appl. Phys. Lett. 1997, 70, 925–927.
Bindra, K.S.; Bookey, H.T.; Kar, A.K.; Wherrett, B.S.; Liu, X.; Jha, A. Nonlinear optical properties of chalcogenide glasses: Observation of multiphoton absorption. Appl. Phys. Lett. 2001, 9, 1939–1941.
Zakery, A.; Elliott, S. Optical properties and applications of chalcogenide glasses: A review. J. Non Cryst. Solids 2003, 330, 1–12.
Sanghera, J.S.; Florea, C.M.; Shaw, L.B.; Pureza, P.; Nguyen, V.Q.; Bashkansky, M.; Dutton, Z.; Aggarwal, I.D. Non-linear properties of chalcogenide glasses and fibers. J. Non Cryst. Solids 2008, 354, 462–467.
Eggleton, B.J. Chalcogenide photonics: Fabrication, devices and applications Introduction. Opt. Express 2010, 18, 26632–26634.
Hewak, D.W.; Brady, D.; Curry, R.J.; Elliott, G.; Huang, C.C.; Hughes, M.; Knight, K.; Mairaj, A.; Petrovich, M.N.; Simpson, R.E.; et al. Chalcogenide glasses for photonics device applications. In Photonic Glasses and Glass-Ceramics; Murugan, G.S., Ed.; Research Signpost: Thiruananthapuram, India, 2010; pp. 29–102.
Hisakumi, H.; Tanaka, K. Giant photoexpansion in As2S3 glass. Appl. Phys. Lett. 1994, 65, 2925.
Zarzycki, J. Glasses and the Vitreous State; Cambridge University Press: Cambridge, UK, 1991.
Minardi, S.; Cheng, G.; D’Amico, C.; Stoian, R. Low-power-threshold photonic saturable absorber in nonlinear chalcogenide glass. Opt. Lett. 2015, 40, 257–259.
Macedo, P.; Napolitano, A. Effects of a distribution of volume relaxation times in the annealing of BSC glass. J. Res. Natl. Bur. Stand. 1967, 71, 231–238.
Calvez, L.; Yang, Z.; Lucas, P. Reversible giant photocontraction in chalcogenide glass. Opt. Express 2009, 17, 18581–18589.
Gretzinger, T.; Fernandez, T.T.; Gross, S.; Arriola, A.; Withford, M.J. Boson band mapping: Revealing ultrafast laser induced structural modifications in chalcogenide glass. Opt. Lett. 2020, 45, 3369–3372.
Lucas, P.; King, E.A. Calorimetric characterization of photoinduced relaxation in GeSe9 glass. J. Appl. Phys. 2006, 100, 023502.
Caulier, O.; Le Coq, D.; Calvez, L.; Bychkov, E.; Masselin, P. Free carrier accumulation during direct laser writing in chalcogenide glass by light filamentation. Opt. Express 2011, 19, 20088–20096.
Hisakumi, H.; Tanaka, K. Optical microfabrication of chalcogenide glasses. Science 1995, 270, 974–975.
Boesch, L.; Napolitano, A.; Macedo, P.B. Spectrum of Volume Relaxation Times in B2O3. J. Am. Ceram. Soc. 1970, 53, 148–153.
Cheng, Y.; Sugioka, K.; Midorikawa, K.; Masuda, M.; Toyoda, K.; Kawachi, M.; Shihoyama, K. Control of the cross-sectional shape of a hollow microchannel embedded in photo-structurable glass by use of a femtosecond laser. Opt. Lett. 2003, 28, 55–57.
Osellame, R.; Taccheo, S.; Marangoni, M.; Ramponi, R.; Laporta, P.; Polli, D.; De Silvestri, S.; Cerullo, G. Femtosecond writing of active optical waveguides with astigmatically shaped beams. J. Opt. Soc. Am. B 2003, 20, 1559–1567.
Keil, R.; Heinrich, M.; Dreisow, F.; Pertsch, T.; Tünnermann, A.; Nolte, S.; Christodoulides, D.N.; Szameit, A. All-optical routing and switching for three-dimensional photonic circuitry. Sci. Rep. 2011, 1, 94.
Minardi, S.; Dreisow, F.; Grüfe, M.; Nolte, S.; Pertsch, T. Three-dimensional photonic component for multichannel coherence measurements. Opt. Lett. 2012, 37, 3030–3130.
Crespi, A.; Osellame, R.; Ramponi, R.; Brod, D.J.; Galvao, E.F.; Spagnolo, N.; Vitelli, C.; Maiorino, E.; Mataloni, P.; Sciarrino, F. Integrated multimode interferometers with arbitrary designs for photonic boson sampling. Nat. Photonics 2013, 7, 545–549.
Vogel, M.M.; Abdou-Ahmed, M.; Voss, A.; Graf, T. Very-large-mode-area single- mode multicore fiber. Opt. Lett. 2009, 34, 2876–2878.
Masselin, P.; Bychkov, E.; Le Coq, D. Direct laser writing of a low-loss waveguide with independent control over the transverse dimension and the refractive index contrast between the core and the cladding. Opt. Lett. 2016, 41, 3507–3510.
Long, X.; Bai, J.; Zhao, W.; Stoian, R.; Hui, R.; Cheng, G. Stressed waveguides with tubular depressed-cladding inscribed in phosphate glasses by femtosecond hollow laser beams. Opt. Lett. 2012, 37, 3138–3140.
Tang, W.; Zhang, W.; Liu, X.; Liu, S.; Stoian, R.; Cheng, G. Tubular depressed cladding waveguide laser realized in Yb: YAG by direct inscription of femto- second laser. J. Opt. 2015, 17, 05803.
Liu, X.; Zhang, W.; Zhao, W.; Stoian, R.; Cheng, G. Expanded-core waveguides written by femtosecond laser irradiation in bulk optical glasses. Opt. Express 2014, 22, 28771–28782.
Le Coarer, E.; Blaize, S.; Benech, P.; Stefanon, I.; Morand, A.; L’erondel, G.; Leblond, G. Wavelength-scale stationary-wave integrated Fourier-transform spectrometry. Nat. Photonics 2007, 1, 473–478.
Thomas, F.; Heidmann, S.; de Mengin, M.; Courjal, N.; Ulliac, G.; Morand, A.; Benech, P.; Le Coarer, E.; Martin, G. First Results in Near and Mid IR Lithium Niobate-Based Integrated Optics Interferometer Based on SWIFTS-Lippmann Concept. J. Light. Technol. 2014, 32, 4338–4344.
Bonneville, C.; Thomas, F.; de Mengin Poirier, M.; LeCoarer, E.; Benech, P.; Gonthiez, T.; Morand, A.; Coutant, O.; Morino, E.; Puget, R.; et al. SWIFTS: A groundbreaking integrated technology for high performances spectroscopy and optical sensors. In Proceedings of the SPIE MOEMS Photonics West, San Francisco, CA, USA, 2–7 February 2013.
Bonduelle, M.; Martin, G.; Perez, I.H.; Morand, A.; D’Amico, C.; Stoian, R.; Zhang, G.; Cheng, G. Laser written 3D 3T spectro-interferometer: Study and optimisation of the laser-written nano-antenna. In Proceedings of the SPIE 11446, Optical and Infrared Interferometry and Imaging VII, 114462T, online, CA, USA, 13 December 2020.
Büttner, T.F.S.; Hudson, D.D.; Mägi, E.C.; Bedoya, A.C.; Taunay, T.; Eggleton, B.J. Multicore, tapered optical fiber for nonlinear pulse reshaping and saturable absorption. Opt. Lett. 2012, 37, 2469–2471.
Bellec, M.; Panagiotopoulos, P.; Papazoglou, D.G.; Efremidis, N.K.; Couairon, A.; Tzortzakis, S. Observation and Optical Tailoring of Photonic Lattice Filaments. Phys. Rev. Lett. 2012, 109, 113905.
Szameit, A.; Blömer, D.; Burghoff, J.; Schreiber, T.; Pertsch, T.; Nolte, S.; Tünnermann, A.; Lederer, F. Discrete nonlinear localization in femtosecond laser written waveguides in fused silica. Opt. Express 2005, 13, 10552–10557.
Minardi, S.; Eilenberger, F.; Kartashov, Y.V.; Szameit, A.; Röpke, U.; Kobelke, J.; Schuster, K.; Bartelt, H.; Nolte, S.; Torner, L.; et al. Three-Dimensional Light Bullets in Arrays of Waveguides. Phys. Rev. Lett. 2010, 105, 263901.
Hudson, D.D.; Shish, K.; Schibli, T.R.; Kutz, J.N.; Christodoulides, D.N.; Morandotti, R.; Cundiff, S.T. Nonlinear femtosecond pulse reshaping in waveguide arrays. Opt. Lett. 2008, 33, 1440–1442.
Snyder, A.W. Coupled-Mode Theory for Optical Fibers. J. Opt. Soc. Am. 1972, 62, 1267–1277.
Zhao, H.; Major, A. Powerful 67 fs Kerr-lens mode-locked prismless Yb:KGW oscillator. Opt. Express 2013, 21, 31846–31851.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Physics, Applied; Physics, Condensed Matter; Optics

Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Ciro D'Amico

View Times: 1.0K

Update Date: 25 Jun 2021

Table of Contents

Video Upload Options

Confirm