
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Giorgio Palma | + 2393 word(s) | 2393 | 2021-06-22 11:20:22 | | | |
| 2 | Peter Tang | Meta information modification | 2393 | 2021-06-25 04:07:35 | | |
Video Upload Options
Metamaterials, man-made composites that are scaled smaller than the wavelength, have demonstrated a huge potential for application in acoustics, allowing the production of sub-wavelength acoustic absorbers, acoustic invisibility, perfect acoustic mirrors and acoustic lenses for hyper focusing, and acoustic illusions and enabling new degrees of freedom in the control of the acoustic field. The zero, or even negative, refractive sound index of metamaterials offers possibilities for the control of acoustic patterns and sound at sub-wavelength scales. The potential of metamaterial-based technologies has recently caught the interest of the aeronautics community. Their effect in the presence of realistic flows in the surrounding domains, with boundary layer, turbulence, is currently a hot research topic. The interaction with flow requires a careful design of the metamaterial to avoid detrimental effects and enabling the device maximum capabilities in aeronautics.
1. Introduction
When both mass density (ρ) and the bulk modulus (K) are negative, an acoustic wave is allowed to propagate inside the medium, thus exhibiting a negative refractive index. This causes energy to flow in the opposite direction with respect to the wave, i.e., the wave vector and the Poynting vector (describing the energy flow associated with the acoustic propagation) point in opposite directions. A metamaterial exposing the negative refraction index can be exploited for applications like acoustic superlenses [4][11], i.e., a device capable of focusing an incident acoustic wave (with a sub-wavelength spacial resolution), even beyond the diffraction limit, in a sub-wavelength spot, and, in general, for bending waves and shaping the acoustic field almost arbitrarily.
Near-total reflection can be obtained when only one of the two material parameters, ρand K, becomes negative. This can be achieved using resonant elements to let ρ turn negative [5], or with a membrane decorated with a resonant mass(es) [12][13][14][15], even without [16][17]. The frequency working range can be tuned, adjusting the weight of the masses, if present, or other constructive parameters to place the resonant effect even in the low frequency range. Stacking more than one metamaterial panel together can be a strategy to obtain a more broadband effect.
Another type of singular negative metamaterial can be obtained when the effective bulk modulus turns negative. In Fang et al. [18], inspired by results obtained in the electromagnetic field, an array of sub-wavelength Helmholtz resonators is used to obtain this effect in the ultrasonic regime. Dipolar and monopolar local resonances were proved to be the essential wave mechanisms for producing, respectively, a negative effective mass density and a negative effective bulk modulus of the metamaterial.
Double negative acoustic metamaterials can be achieved by combining negative density and negative compressibility materials, or by overlapping monopolar and dipolar resonances in the same frequency range, or to design phononic crystals to generate a band folding through multiple scattering in a periodic structure.
Different and more complex devices with equivalent dynamic or electromagnetic lumped models have been developed so far [19] to obtain metamaterials, based on locally resonant elements that show single or double negativity, depending on the considered frequency working range [19][20][21].
Other approaches have also been successfully adopted to realize metamaterials with interesting properties, such as coiling up space by using labyrinthine structures to introduce local phase delay in sound propagation. The phase shift can be designed in the full 0–2π range to obtain flat surfaces to act as arbitrarily-shaped virtual surfaces [22][23][24], modifying the reflection angle, or it could be random to maximize acoustic diffusion [25][26] (Figure 1). Space-coiling metamaterials can be adopted to obtain lens-like behaviors or even to transform the propagation pattern from spherical to plane waves [27][28]. Furthermore, this approach allows for an effective dynamic ρ<0 and K<0, and hence, a negative refractive index to be obtained in the deep sub-wavelength regime with a quite simple device [29][30].
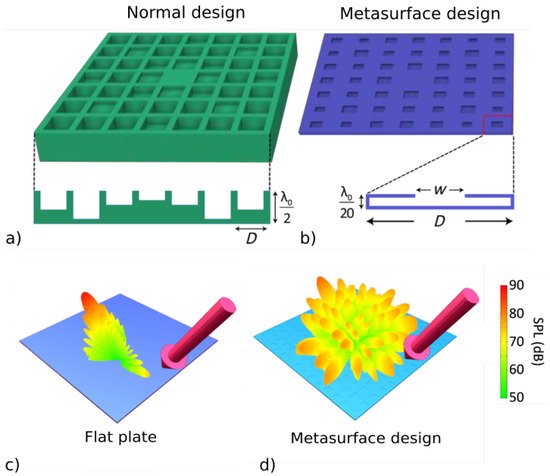
Thermo-viscous losses at the solid–fluid interfaces inside metamaterial components are crucial in determining the behavior of metamaterials. This is particularly true for concepts that consider micro-slits, micro-cavities and/or narrow channels as part of the design, like space-coiling metamaterials. The visco-thermal loss mechanism becomes non-negligible even when the widths of the slits are about two order of magnitude bigger than the viscous and thermal boundary layers (in the order of 10−5 m) and is enhanced by the fact that high amplitude standing waves can form in small cavities. Such losses can deeply modify the expected behavior of the metamaterial under study and hence, should be carefully taken into account and exploited when dissipation and absorption are sought [37][38]. The geometric parameters of a metamaterial can even be tuned to achieve high transmission, high absorption or high reflection from the same basic concept [39].
2. Potential Applications of Aeroacoustic Metamaterials
3. Challenges
References
- Weiglhofer, W.S.; Lakhtakia, A. Introduction to Complex Mediums for Optics and Electromagnetics; SPIE Publications: Bellingham, WA, USA, 1999.
- Cui, T.J.; Smith, D.; Liu, R. Metamaterials; Springer: Berlin/Heidelberg, Germany, 2010.
- Veselago, V.G. The electrodynamics of substances with simultaneously negative values of ϵ and μ. Sov. Phys. Uspekhi 1968, 10, 509.
- Pendry, J.B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 2000, 85, 3966.
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally Resonant Sonic Materials. Science 2000, 289, 1734–1736.
- Li, J.; Chan, C.T. Double-negative acoustic metamaterial. Phys. Rev. E 2004, 70, 055602.
- Ding, Y.; Liu, Z.; Qiu, C.; Shi, J. Metamaterial with Simultaneously Negative Bulk Modulus and Mass Density. Phys. Rev. Lett. 2007, 99, 093904.
- Brunet, T.; Merlin, A.; Mascaro, B.; Zimny, K.; Leng, J.; Poncelet, O.; Aristégui, C.; Mondain-Monval, O. Soft 3D acoustic metamaterial with negative index. Nat. Mater. 2014, 14, 384.
- Lee, S.H.; Wright, O.B. Origin of negative density and modulus in acoustic metamaterials. Phys. Rev. B 2016, 93, 024302.
- Ma, G.; Sheng, P. Acoustic metamaterials: From local resonances to broad horizons. Sci. Adv. 2016, 2, e1501595.
- Zhang, S.; Yin, L.; Fang, N. Focusing Ultrasound with an Acoustic Metamaterial Network. Phys. Rev. Lett. 2009, 102, 194301.
- Yang, Z.; Mei, J.; Yang, M.; Chan, N.H.; Sheng, P. Membrane-Type Acoustic Metamaterial with Negative Dynamic Mass. Phys. Rev. Lett. 2008, 101, 204301.
- Yang, Z.; Dai, H.M.; Chan, N.H.; Ma, G.C.; Sheng, P. Acoustic metamaterial panels for sound attenuation in the 50–1000 Hz regime. Appl. Phys. Lett. 2010, 96, 041906.
- Langfeldt, F.; Riecken, J.; Gleine, W.; Von Estorff, O. A membrane-type acoustic metamaterial with adjustable acoustic properties. J. Sound Vib. 2016, 373, 1–18.
- Mei, J.; Ma, G.; Yang, M.; Yang, Z.; Wen, W.; Sheng, P. Dark acoustic metamaterials as super absorbers for low-frequency sound. Nat. Commun. 2012, 3, 756.
- Cselyuszka, N.; Sečujski, M.; Crnojević-Bengin, V. Novel negative mass density resonant metamaterial unit cell. Phys. Lett. A 2015, 379, 33–36.
- Sheng, P. Coupled membranes with doubly negative mass density and bulk modulus. J. Acoust. Soc. Am. 2013, 134, 4026.
- Fang, N.; Xi, D.; Xu, J.; Ambati, M.; Srituravanich, W.; Sun, C.; Zhang, X. Ultrasonic metamaterials with negative modulus. Nat. Mater. 2006, 5, 452–456.
- Liu, X.N.; Hu, G.K.; Huang, G.L.; Sun, C.T. An elastic metamaterial with simultaneously negative mass density and bulk modulus. Appl. Phys. Lett. 2011, 98, 251907.
- Graciá-Salgado, R.; García-Chocano, V.M.; Torrent, D.; Sánchez-Dehesa, J. Negative mass density and ρ-near-zero quasi-two-dimensional metamaterials: Design and applications. Phys. Rev. B 2013, 88, 224305.
- Lee, S.H.; Park, C.M.; Seo, Y.M.; Wang, Z.G.; Kim, C.K. Composite Acoustic Medium with Simultaneously Negative Density and Modulus. Phys. Rev. Lett. 2010, 104, 054301.
- Li, Y.; Liang, B.; Gu, Z.M.; Zou, X.Y.; Cheng, J.C. Reflected wavefront manipulation based on ultrathin planar acoustic metasurfaces. Sci. Rep. 2013, 3, 2546.
- Li, Y.; Jiang, X.; Li, R.Q.; Liang, B.; Zou, X.Y.; Yin, L.L.; Cheng, J.C. Experimental Realization of Full Control of Reflected Waves with Subwavelength Acoustic Metasurfaces. Phys. Rev. Appl. 2014, 2, 064002.
- Zhu, Y.F.; Fan, X.D.; Liang, B.; Yang, J.; Yang, J.; Yin, L.l.; Cheng, J.C. Multi-frequency acoustic metasurface for extraordinary reflection and sound focusing. AIP Adv. 2016, 6, 121702.
- Gu, Z.M.; Liang, B.; Zou, X.Y.; Cheng, J.C. Broadband diffuse reflections of sound by metasurface with random phase response. EPL (Europhys. Lett.) 2015, 111, 64003.
- Zhu, Y.; Fan, X.; Liang, B.; Cheng, J.; Jing, Y. Ultrathin Acoustic Metasurface-Based Schroeder Diffuser. Phys. Rev. X 2017, 7, 021034.
- Wang, W.; Xie, Y.; Konneker, A.; Popa, B.I.; Cummer, S.A. Design and demonstration of broadband thin planar diffractive acoustic lenses. Appl. Phys. Lett. 2014, 105, 101904.
- Xie, Y.; Wang, W.; Chen, H.; Konneker, A.; Popa, B.I.; Cummer, S.A. Wavefront modulation and subwavelength diffractive acoustics with an acoustic metasurface. Nat. Commun. 2014, 5, 5553.
- Liang, Z.; Feng, T.; Lok, S.; Liu, F.; Ng, K.B.; Chan, C.H.; Wang, J.; Han, S.; Lee, S.; Li, J. Space-coiling metamaterials with double negativity and conical dispersion. Sci. Rep. 2013, 3, 1614.
- Tang, K.; Qiu, C.; Ke, M.; Lu, J.; Ye, Y.; Liu, Z. Anomalous refraction of airborne sound through ultrathin metasurfaces. Sci. Rep. 2014, 4, 6517.
- Zhai, S.; Chen, H.; Ding, C.; Shen, F.; Luo, C.; Zhao, X. Manipulation of transmitted wave front using ultrathin planar acoustic metasurfaces. Appl. Phys. A 2015, 120, 1283–1289.
- Christensen, J.; Martín-Moreno, L.; García-Vidal, F.J. All-angle blockage of sound by an acoustic double-fishnet metamaterial. Appl. Phys. Lett. 2010, 97, 134106.
- Zhao, J.; Li, B.; Chen, Z.N.; Qiu, C.W. Redirection of sound waves using acoustic metasurface. Appl. Phys. Lett. 2013, 103, 151604.
- Zhao, S.D.; Wang, Y.S.; Zhang, C. A continuously tunable acoustic metasurface for transmitted wavefront manipulation. arXiv, 2017; arXiv:1711.09701.
- Díaz-Rubio, A.; Tretyakov, S.A. Acoustic metasurfaces for scattering-free anomalous reflection and refraction. Phys. Rev. B 2017, 96, 125409.
- Leroy, V.; Strybulevych, A.; Lanoy, M.; Lemoult, F.; Tourin, A.; Page, J.H. Superabsorption of acoustic waves with bubble metascreens. Phys. Rev. B 2015, 91, 020301.
- Starkey, T.A.; Smith, J.D.; Hibbins, A.P.; Sambles, J.R.; Rance, H.J. Thin structured rigid body for acoustic absorption. Appl. Phys. Lett. 2017, 110, 041902.
- Cai, X.; Guo, Q.; Hu, G.; Yang, J. Ultrathin low-frequency sound absorbing panels based on coplanar spiral tubes or coplanar Helmholtz resonators. Appl. Phys. Lett. 2014, 105, 121901.
- Molerón, M.; Serra-Garcia, M.; Daraio, C. Visco-thermal effects in acoustic metamaterials: From total transmission to total reflection and high absorption. New J. Phys. 2016, 18, 033003.
- Gaborit, M.; Schwan, L.; Dazel, O.; Groby, J.P.; Weisser, T.; Göransson, P. Coupling FEM, Bloch Waves and TMM in Meta Poroelastic Laminates. Acta Acust. United Acust. 2018, 104, 220–227.
- Gao, K. Multiscale Modelling of Acoustic Porous Materials. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 2016.
- Roca, D.; Lloberas-Valls, O.; Cante, J.; Oliver, J. A computational multiscale homogenization framework accounting for inertial effects: Application to acoustic metamaterials modelling. Comput. Methods Appl. Mech. Eng. 2018, 330, 415–446.
- Sridhar, A.; Kouznetsova, V.G.; Geers, M.G.D. Homogenization of locally resonant acoustic metamaterials towards an emergent enriched continuum. Comput. Mech. 2016, 57, 423–435.




