Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Yuichi Nakamura
 + 2129 word(s) 2129 2021-06-03 07:37:04 |
2 format correct
Nora Tang
 Meta information modification 2129 2021-06-24 05:52:43 |

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Nakamura, Y. Magnetic Holography. Encyclopedia. Available online: https://encyclopedia.pub/entry/11224 (accessed on 29 November 2024).
Nakamura Y. Magnetic Holography. Encyclopedia. Available at: https://encyclopedia.pub/entry/11224. Accessed November 29, 2024.
Nakamura, Yuichi. "Magnetic Holography" Encyclopedia, https://encyclopedia.pub/entry/11224 (accessed November 29, 2024).
Nakamura, Y. (2021, June 24). Magnetic Holography. In Encyclopedia. https://encyclopedia.pub/entry/11224
Nakamura, Yuichi. "Magnetic Holography." Encyclopedia. Web. 24 June, 2021.
Magnetic Holography
Edit
This entry is adapted from the peer-reviewed paper 10.3390/photonics8060187

The principle of magnetic holograms and its application to holographic memory are reviewed. A magnetic hologram was recorded through a thermomagnetic recording as a difference in magnetization direction and reconstructed with the magneto-optical effect. To achieve a bright reconstruction image, it is important to record deep magnetic fringes on the materials with large Faraday rotation coefficients. This technique was applied to the holographic memory using transparent magnetic garnets as a recording material. The first reconstruction image was dark and noisy, but improvements in the recording conditions resulted in error-free recording and reconstruction of the magnetic hologram. To form deep magnetic fringes, insertion of heat dissipation (HD) layers into recording layer was proposed. It was found that this HD multilayer medium showed diffraction efficiency higher than that of a single layer medium, and error-free recording and reconstruction were also achieved, using magnetic assisted recording. These results suggest that HD multilayer media have potential applications in recording media of magnetic holographic data storage. In future, a high recording density technique, such as multiple recording, should be developed.

magnetic hologram magneto-optical effect thermomagnetic recording magnetic holographic memory

1. Introduction

Holography is a technology that records and reconstructs light from an object (object or signal light), using interference and diffraction. The light from the object and the reference light interfere with each other, and this interference pattern, recorded on a recording medium, is called a hologram. When only the reference light is irradiated on this hologram, the waveform of the original light from the object is reconstructed as it is through diffraction by the interference fringes. Therefore, holography is an ideal three-dimensional image reconstruction technique because the image reconstructed from the hologram can be seen as it is, even if the viewing angle is changed. In holography, the interference fringes are recorded volumetrically, and the signal light can be reconstructed one by one from the holograms recorded in the same place with slightly different conditions, for example, by changing the angle or phase of the reference and signal lights because the interference conditions are strict. Holographic technology is expected to be applied to holographic data storage with large capacity and a high data transfer rate since a large amount of data can be recorded in the same place and reconstructed at once by showing two-dimensional data as the signal light [1][2][3][4][5][6][7][8][9][10][11][12][13][14][15][16][17].
There are various types of holography, but two methods are mainly used as optical interference systems for the recording and reconstruction of holographic memory; one is the two-beam interference method in which signal and reference lights are irradiated from different angles and interfered (Figure 1a), and the other is the collinear (or coaxial) holographic interference method in which signal and reference lights are formed in a spatial light modulator (SLM) and interfered in the same axis (Figure 1b) [12][13][14][15][16][17]. In general, the former is widely used, while the latter can use a similar optical system to that of the conventional Digital Versatile Disc and the Blu-ray Disc and has an advantage against vibration.
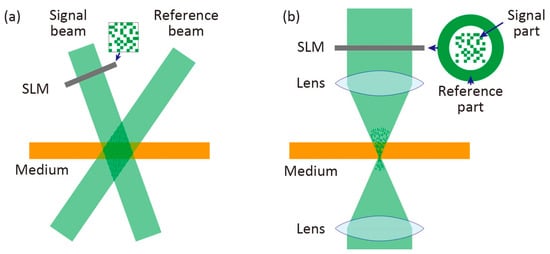
Photonics 08 00187 g001 550
Figure 1. Schematics of (a) two-beam interference method and (b) collinear interference method.
A photoreactive photopolymer is generally used for hologram recording material, and a hologram is formed as a difference in the refractive index of the material, in general. This shows large diffraction efficiency, which is an index of the brightness of the reconstruction image, while there are issues with the volume change associated with the photoreaction and material stability. Contrastingly, a magnetic hologram that is formed as the difference in the magnetization direction of a recording magnetic material was proposed by Mezrich [18] in 1969. Magnetic holograms are recorded by a thermomagnetic recording (Curie point writing) method [18][19][20][21][22] and reconstructed using the rotation of the polarization plane through a magneto-optical effect [18][20][21][22][23].
We developed magnetic holograms and their application technologies, using transparent bismuth substituted rare earth iron garnet (Bi:RIG) as the recording material [24][25][26][27][28][29][30][31][32][33][34]. Since magnetic garnet is an oxide, it is substantially a very stable recording material, and by recording on a magnetic material with appropriate translucency, it is possible to record volumetric holograms. Holographic memory using this as a recording material is also expected to realize a rewritable (reformattable) hologram memory, and there are no issues of volume change and shading that may occur with photopolymers. In this paper, the principle of magnetic holograms and its application to magnetic hologram memory are reviewed.

2. Principles of Recording and Reconstruction of Magnetic Holography

2.1. Recording of Magnetic Hologram

The thermomagnetic recording method is used for recording magnetic holograms. Figure 2 schematically shows the recording process of a magnetic hologram. Reference and signal beams are irradiated on a perpendicularly magnetized film, and the intensity distribution of light is formed due to light interference. The temperature distribution is formed corresponding to the light intensity distribution through the absorption of light, and the magnetization of the regions exceeding the Curie temperature, TC, disappears. In the subsequent cooling process, the direction of magnetization is reversed by stray magnetic fields from the surrounding magnetization, so that a magnetic hologram is formed as the difference in the direction of magnetization.
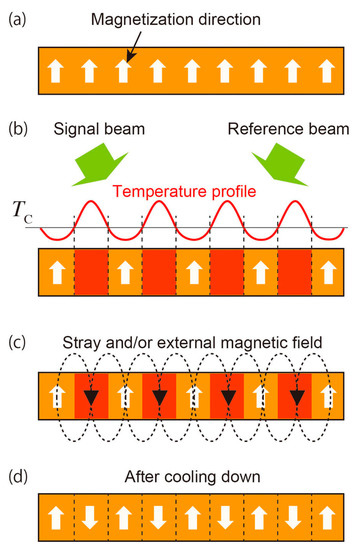
Photonics 08 00187 g002 550
Figure 2. Schematics of recording process of magnetic hologram. (a) Perpendicularly magnetized recording medium. (b) As the result of interference, the medium is locally heated up higher than Curie temperature, TC, by the absorption of light. (c) The magnetization of the heated region is reversed by stray and/or external magnetic fields during cooling. (d) The interference pattern of light can be recorded as the difference in the direction of magnetization.
The effect of heat generated by the absorption of light is important to form clear magnetic fringes by thermomagnetic recording. The magnetic hologram is formed by the thermally demagnetized regions where the temperature exceeds the Curie temperature due to the absorption of light, while this heat diffuses to the low temperature regions in the magnetic film. This heat diffusion effect becomes greater in the case of recording on the materials with large heat conduction, especially in the metal film. In this case, if the energy density for recording is small, the generated heat diffuses before the temperature rises to the Curie temperature, and the temperature of the entire film rises; therefore, we cannot obtain a clear magnetic fringe. Chen et al. reported that the pulse width of the laser should be on the order of 10 ns or less to form magnetic fringes on MnBi films [35]. Nakamura et al. [25] also reported the effect of the period of the interference fringe and the pulse width of the laser radiation on the shape of the magnetic fringe in a magnetic garnet film with low thermal conductivity with a numerical simulation. They reported that the depth of the magnetic fringe of 500 line-pair/mm, in which the period of the interference fringe is 2 µm, is deeper than that of 1500 line-pair/mm in which the period of the interference fringe is 0.667 µm; a laser pulse of 50 ps is desirable for recording clear and deep magnetic fringes of 1500 line-pair/mm, compared to 25 ns. These results show that lateral thermal diffusion during thermomagnetic recording is important for the formation of magnetic fringes, that is, the wider the distance between fringes, the smaller the effect of thermal diffusion; the effect of thermal diffusion during irradiation can be reduced, using the high energy and short pulse laser. In addition, Lee et al. [36] reported that when the average temperature in the film during thermomagnetic recording exceeds the Curie temperature, the magnetization of the entire region disappears. Therefore, the total recording energy should not be too large. This heat diffusion effect is discussed later in Section 3.3, and a method reducing this effect to form deep magnetic fringes is proposed.

2.2. Reconstruction from Magnetic Hologram

The magneto-optical effect is used for reconstruction of a magnetic hologram. The magneto-optical effect is a phenomenon in which the polarization plane rotates depending on the direction and strength of magnetization when linearly polarized light is incident on a magnetic material. The magneto-optical effect on transmitted light is called the Faraday effect, and that on reflected light is called the Kerr effect. Figure 3 schematically shows the reconstruction principle for transmitted light. When linearly polarized light is incident on the magnetic grating, the polarization plane rotates in the opposite direction depending on the direction of magnetization. At this time, when we see the component in the direction orthogonal to the polarization plane of incident light, the light has a phase difference of 180°. When the reference light is incident on the magnetic hologram, this component of the diffracted light interferes with each other, so that the signal light is reconstructed by the principle of the phase hologram [21][22][23]. The S/N ratio of the reconstructed light can be improved, therefore, by separating only the component orthogonal to the incident light polarization plane, using the analyzer [18].
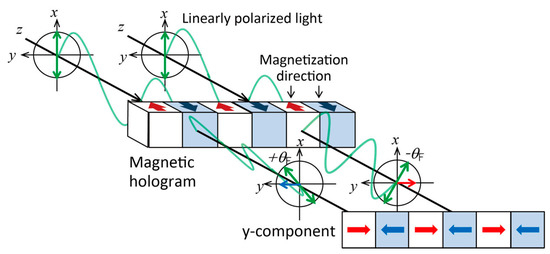
Photonics 08 00187 g003 550
Figure 3. Principle of the reconstruction of magnetic hologram.
Hascal [23] discussed in detail the reconstruction principle and diffraction efficiency of magnetic holograms. In a binary magnetic hologram, the polarization plane of diffracted light is orthogonal to that of the incident light. On the other hand, in a magnetic hologram with magnetization distribution, such as a trigonometric function, an even order diffracted light, including the 0th order transparent light, has a polarization plane that is the same as that of the incident light, while the polarization plane of the odd order diffracted light is orthogonal to that of the incident light. In either case, the strength of the diffracted light of the second order or higher is sufficiently weak, so the first order diffraction light that has a polarized plane orthogonal to the incident light is used. Theoretically, the diffraction efficiency η of the first-order diffracted light is described as follows:
η = sin2(θF) ~ θF2 = (Ft)2
with the rotation angle θF of the magnetic hologram as θF = Ft, where F is the Faraday rotation coefficient representing the rotation angle per unit thickness, and t is the depth of the magnetic hologram, respectively. This diffraction efficiency η is an index of the brightness of the reconstructed image, and a bright reconstructed image can be obtained by forming a deep volumetric magnetic hologram on the recording material with a large rotation angle per unit thickness. Equation (1) shows that the diffraction efficiency decreases when the Faraday rotation angle exceeds 90 degrees. However, for example, the Faraday rotation angle of a typical bismuth-substituted rare earth iron garnet is about several deg./µm at a wavelength of 532 nm, and, as will be described later, the recording depth by thermomagnetic recording is about 1 to 2 µm. On the other hand, magnetic metal films, such as MnBi, show a rotation angle of several tens of deg./µm, while the recording depth is only 100 nm or less due to large light absorption. Hence, we need not worry that the rotation angle becomes too large since the rotation angle of the magnetic hologram will be less than 10 degrees. Therefore, the recording conditions for recording the magnetic hologram as deeply as possible are desirable.
Tanaka et al. [37] recorded interference fringes on the Bi–Mn film by the two-beam interference method and experimentally showed that the diffraction efficiency was proportional to the 2.3rd power of the Faraday rotation angle, which is in good agreement with the theory. In addition, Chen et al. [35][38] recorded and reconstructed a two-dimensional dot pattern on the Bi–Mn film and proved that complex two-dimensional patterns can be recorded and constructed with magnetic holograms. Nakamura et al. [25] reported that the diffraction efficiency of the magnetic fringe with 500 line-pair/mm was larger than that with 1500 line-pair/mm. The diffraction efficiency is theoretically independent of the fringe spacing, but the depth of the magnetic fringe with 500 line-pair/mm was deeper than that with 1500 line-pair/mm from the numerical simulation as mentioned in Section 2.1. Therefore, this large diffraction efficiency was thought to be attributed to the deep magnetic fringe from Equation (1).

3. Conclusions

The principle of magnetic holography and the development of the magnetic hologram memory were reviewed. The magnetic hologram is recorded by the thermomagnetic recording method and reconstructed with the magneto-optical effect. Therefore, a bright reconstruction image is achieved by recording a deep magnetic hologram in the recording material with a large Faraday rotation coefficient. Although the first reconstruction image was dark and noisy, the improvement in the recording conditions resulted in error-free recording and reconstruction of the magnetic hologram. In addition, HD multilayer media were proposed to avoid the merging of the magnetic fringes and to form a deep magnetic hologram. The properly designed HD multilayer medium showed that the diffraction efficiency is larger than that of the usual single-layer film. Error-free recording and reconstruction were also achieved, using the magnetic assisted recording technique. This suggests that the HD multilayer media have potential applications in the recording media of magnetic holographic data storage and are suitable for volumetric hologram recording, which is advantageous for multiple recordings. In future, the development of a high recording density technique, such as multiple recording, is expected.

References

  1. Mikaeliane, A.L.; Bobrinev, V.I. Holographic memory devices. Opto Electron. 1970, 2, 193–199.
  2. Rajchman, J.A. An Optical Read-Write Mass Memory. Appl. Opt. 1970, 9, 2269–2271.
  3. Sakaguchi, M.; Nishida, N.; Nemoto, T. A New Associative Memory System Utilizing Holography. IEEE Trans. Comput. 1970, C-19, 1174–1181.
  4. Takeda, Y. Hologram memory with high quality and high information storage density. Jpn. J. Appl. Phys. 1972, 11, 656–665.
  5. D’auria, L.; Huignard, J.; Spitz, E. Holographic read-write memory and capacity enhancement by 3-Dstorage. IEEE Trans. Magn. 1973, 9, 83–94.
  6. Nomura, H.; Okoshi, T. Storage density limitation of a volume-type hologram memory: Theory. Appl. Opt. 1976, 15, 550–555.
  7. Hong, J.H.; McMichael, I.; Chang, T.V.; Christian, Q.; Paek, E.G. Volume holographic memory systems: Techniques and architectures. Opt. Eng. 1995, 34, 2193–2203.
  8. Rakuljic, G.A.; Leyva, V.; Yariv, A. Optical data storage using orthogonal wavelength multiplexed volume holograms. Opt. Lett. 1992, 17, 1471–1473.
  9. Li, H.-Y.S.; Psaltis, D. Three-dimensional holographic disks. Appl. Opt. 1994, 33, 3764–3774.
  10. Pu, A.; Psaltis, D. High-density recording in photopolymer-based holographic three-dimensional disks. Appl. Opt. 1996, 35, 2389–2398.
  11. Orlov, S.S.; Phillips, W.; Bjornson, E.; Takashima, Y.; Sundaram, P.; Hesselink, L.; Okas, R.; Kwan, D.; Snyder, R. High-transfer-rate high-capacity holographic disk data-storage system. Appl. Opt. 2004, 43, 4902–4914.
  12. Horimai, H.; Tan, X. Holographic versatile disc system. Proc. SPIE 2005, 5939, 593901.
  13. Horimai, H.; Tan, X.; Li, J.; Suzuki, K. Wavelength margin analysis in advanced collinear holography. Jpn. J. Appl. Phys. 2005, 44, 3493–3494.
  14. Horimai, H.; Tan, X.; Li, J. Collinear holography. Appl. Opt. 2005, 44, 2575–2579.
  15. Horimai, H.; Tan, X. Advanced collinear holography. Opt. Rev. 2005, 12, 90–92.
  16. Horimai, H.; Tan, X. Collinear technology for a holographic versatile disk. Appl. Opt. 2006, 45, 910–914.
  17. Horimai, H.; Tan, X. Holographic information storage system: Today and future. IEEE Trans. Magn. 2007, 43, 943–947.
  18. Mezrich, R.S. Curie-point writing of magnetic holograms on MnBi. Appl. Phys. Lett. 1969, 14, 132–134.
  19. Mayer, L. Curie-Point Writing on Magnetic films. J. Appl. Phys. 1958, 29, 1003.
  20. Fan, G.; Pennington, K.; Greiner, J.H. Magneto-Optic Hologram. J. Appl. Phys. 1969, 40, 974–975.
  21. Mezrich, R.S. Magnetic Holography. Appl. Opt. 1970, 9, 2275–2279.
  22. Mezrich, R.S. Reconstruction Effects in Magnetic Holography. IEEE Trans. Magn. 1970, 6, 537–541.
  23. Hascal, H.M. Polarization and Efficiency in Magnetic Holography. IEEE Trans. Magn. 1970, 6, 542–545.
  24. Nakamura, Y.; Takagi, H.; Lim, P.B.; Inoue, M. Magnetic volumetric hologram memory with magnetic garnet. Opt. Express 2014, 22, 16439–16444.
  25. Nakamura, Y.; Takagi, H.; Lim, P.B.; Inoue, M. Effect of recording condition on the diffraction efficiency of magnetic hologram with magnetic garnet films. J. Appl. Phys. 2014, 116, 103106.
  26. Isogai, R.; Sagara, N.; Goto, T.; Nakamura, Y.; Lim, P.B.; Inoue, M. Diffraction efficiency of volumetric magnetic holograms with Magnetophotonic crystals. J. Mag. Soc. Jpn. 2014, 38, 119–122.
  27. Isogai, R.; Goto, T.; Takagi, H.; Nakamura, Y.; Lim, P.B.; Inoue, M. Effect of structure and properties of magnetic material on diffraction efficiency of magnetophotonic crystal media for magnetic volumetric holography. J. Mag. Soc. Jpn. 2015, 39, 33–36.
  28. Isogai, R.; Suzuki, S.; Nakamura, K.; Nakamura, Y.; Takagi, H.; Goto, T.; Lim, P.B.; Inoue, M. Collinear volumetric magnetic holography with magnetophotonic microcavities. Opt. Express 2015, 23, 13153–13158.
  29. Isogai, R.; Nakamura, Y.; Takagi, H.; Goto, T.; Lim, P.B.; Inoue, M. Thermomagnetic writing into magnetophotonic microcavities controlling thermal diffusion for volumetric magnetic holography. Opt. Express 2016, 24, 522–527.
  30. Nakamura, Y.; Shirakashi, Z.; Takagi, H.; Lim, P.B.; Goto, T.; Uchida, H.; Inoue, M. Error-free reconstruction of magnetic hologram via improvement of recording conditions in collinear optical system. Opt. Express 2017, 25, 15349–15357.
  31. Shirakashi, Z.; Goto, T.; Takagi, H.; Nakamura, Y.; Lim, P.B.; Uchida, H.; Inoue, M. Reconstruction of non-error magnetic hologram data by magnetic assist recording. Sci. Rep. 2017, 7, 12835.
  32. Nakamura, Y.; Lim, P.B.; Goto, T.; Uchida, H.; Inoue, M. Recording and reconstruction of volumetric magnetic hologram using multilayer medium with heat dissipation layers. Opt. Express 2019, 27, 27573–27579.
  33. Nakamura, Y.; Lim, P.B.; Goto, T.; Uchida, H.; Inoue, M. Development of Heat Dissipation Multilayer Media for Volumetric Magnetic Hologram Memory. Appl. Sci. 2019, 9, 1738.
  34. Nakamura, Y.; Lim, P.B.; Goto, T.; Uchida, H.; Inoue, M. Development of heat dissipation multilayer media for magnetic hologram memory. Electron. Comm. Jpn. 2020, 103, 22–29.
  35. Chen, D.; Otto, G.N.; Schmit, F.M. MnBi Films for Magnetooptic Recording. IEEE Trans. Magn. 1973, 9, 66–83.
  36. Lee, T.C.; Chen, D. Writing characteristics of MnBi films for Holographic recording. Appl. Phys. Lett. 1971, 19, 62–65.
  37. Tanaka, M.; Ito, T.; Nishimura, Y. Diffraction Efficiency of Magnetic Hologram. IEEE Trans. Magn. 1972, 8, 523–525.
  38. Aagard, R.L.; Lee, T.C.; Chen, D. Advanced optical storage techniques for computers. Appl. Opt. 1972, 11, 2133–2139.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Engineering, Electrical & Electronic
Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Yuichi Nakamura
View Times: 1.2K
Revisions: 2 times (View History)
Update Date: 24 Jun 2021
Table of Contents
    1000/1000
    Hot Most Recent
    ScholarVision Creations
    Feedback