You're using an outdated browser. Please upgrade to a modern browser for the best experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Ngoc Hoang Tran | + 2211 word(s) | 2211 | 2021-06-17 05:06:32 | | | |
| 2 | Bruce Ren | -21 word(s) | 2190 | 2021-06-24 03:17:07 | | |
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Tran, N.H. Geant4-DNA Modeling of Water Radiolysis. Encyclopedia. Available online: https://encyclopedia.pub/entry/11208 (accessed on 03 January 2026).
Tran NH. Geant4-DNA Modeling of Water Radiolysis. Encyclopedia. Available at: https://encyclopedia.pub/entry/11208. Accessed January 03, 2026.
Tran, Ngoc Hoang. "Geant4-DNA Modeling of Water Radiolysis" Encyclopedia, https://encyclopedia.pub/entry/11208 (accessed January 03, 2026).
Tran, N.H. (2021, June 23). Geant4-DNA Modeling of Water Radiolysis. In Encyclopedia. https://encyclopedia.pub/entry/11208
Tran, Ngoc Hoang. "Geant4-DNA Modeling of Water Radiolysis." Encyclopedia. Web. 23 June, 2021.
Copy Citation
In this work, we use the next sub-volume method (NSM) to investigate the possibility of using the compartment-based (“on-lattice”) model to simulate water radiolysis.
water radiolysis
RDME
Gillespie
NSM
Geant4-DNA
1. Introduction
The energy transfer induced by ionizing radiation in a water medium occurs rapidly (on a scale of femtoseconds (fs)) during the physical stage of water radiolysis and is followed by the formation of radiolytic species. These species are created in a very short time (from femtoseconds (fs) to picoseconds (ps)), mainly through electronic events during the physico-chemical stage [1][2][3][4]. These events—such as thermalization, solvation of sub-excitation electrons, electronic hole migration, and fast electronic recombination—can lead to chemical bond breaks and produce species. After this stage, the chemical stage starts with heterogeneous distributions of radiation-induced spurs along the axis of the tracks from a few picoseconds (ps) to greater than ~100 nanoseconds (ns) in water at room temperature [5]. The spur evolution largely depends on the spatial distribution of these high concentration regions. Methods using Brownian dynamics and Smoluchowski theory have been applied to describe the spur evolution, in which detailed individual trajectories of spherical particles are simulated in chemical reaction-diffusion systems (called "systems" in the following text) [5][6][7][8][9]. In this particle-based representation, only the molecules of interest are explicitly simulated, and the solvent (water) is considered a continuum. Under these conditions, the diffusion of the species occurs until two individual reactants encounter each other (chemical interactions happen when the distance between reactants is less than a pre-defined distance). Over time, the species and their products disperse and are distributed more homogeneously. Their reactions continuously occur until they reach steady-states, where the species concentrations do not change anymore (from 100 microseconds (µs) to several seconds (s)).
Although the detail level is limited when using simplifications (spherical particles, continuum representation), the calculation time remains the main drawback of the particle-based representation when the simulations deal with a large number of species. This makes it difficult to simulate large, absorbed dose radiation systems, where the concentration of produced species may significantly impact the irradiated medium composition. Moreover, the majority of radiation chemistry experiments extend up to the homogeneous regime where radiation-induced species evolve and reach steady-states over long-term scales [5]. Because of its computational cost, the particle-based representation cannot simulate these types of conditions. Instead, compartment-based models can be used because the level of detail is more limited [10].
The compartment-based representation describes species evolution by gathering molecules of the same species as one group placed in a confined volume (or “compartment”). Only molecules in the compartment can react with each other. A basic requirement of compartment-based models is that the distribution of the species is a homogeneous mixture or “well-mixed” in their compartment. Therefore, no information about species positions is described during the evolution. Under this condition, the chemical master equation (CME) [11] is used to describe the time–evolution probability of all the different possible states of the system. In general, the CME is mathematically troublesome. To address this, Gillespie developed a stochastic simulation algorithm (SSA) that equivalently reproduces the CME using a derived Monte Carlo technique [11].
In practice, this “well-mixed” condition is usually not fulfilled since most systems of interest do not begin in homogeneous states. Many of them are first heterogeneously distributed and then tend toward homogeneity as the systems evolve over time, before reaching the fully well-mixed state. For example, in water radiolysis, the transition process between the heterogeneous and homogeneous states may occur continuously from ns to µs or longer, depending on the volume and initial species distribution. Therefore, to be able to apply this well-mixed condition to heterogeneous systems, the compartment-based model proposes dividing the simulation volume into smaller regions (“sub-volume” or “voxels”). In these voxels, the species can be considered as well-mixed (or locally homogeneous). The species can react with each other in the same voxel, and diffusion is modeled by jumps between adjacent voxels. An extension of the CME is the reaction-diffusion master equation (RDME) [12], which is used to account for spatial distributions of species into the states of the system.
2. Simulation of Diffusion
In this test, we simulated the diffusion of solvated electrons (e−aq) in a 0.2 × 0.2 × 0.2 µm3 water cubic volume without chemical reactions taking place. In the compartment-based simulation, the water volume was split into a mesh of 213 voxels with a voxel size of (h=0.2/21μm) kept constant over time. The simulation started with 200 e−aq molecules placed randomly in the central voxel of the mesh. The diffusion coefficient of the solvated electron was set to D=4.9×10−9 m2 s−1, reflecting a temperature of 25 °C. The NSM algorithm is only used for diffusion. Figure 1 shows the comparison of spatial distributions of e−aq species at time 10 ns, 20 ns, 50 ns, and 100 ns obtained by the compartment-based and the particle-based SBS models. For the particle-based model, since the cubic volume is chosen large enough, we processed four different simulations with one single time step of 10 ns, 20 ns, 50 ns, and 100 ns [6]. We obtained a general good agreement between the results obtained with the compartment-based and the particle-based simulations.

Figure 1. Comparison of spatial (radial) distributions of solvated electrons diffusing in water as computed with the RDME method (blue histogram with unbold error bars) and the SBS method implemented in Geant4-DNA (solid line with bold error bars). The distributions are computed at 10 ns, 20 ns, 50 ns, and 100 ns.
3. Simulation of a Simple Reaction-Diffusion System
For the second benchmark, we investigated a simplified reaction-diffusion system. We considered the same simulation setup with the exception that the solvated electrons did not only diffuse in water but could also interact with each other (Reaction 9 in Table 3). The resolution of the initial mesh in the compartment-based model should be set small enough to ensure that the molecules are well-mixed in each voxel at the start of the simulation. This condition is fulfilled if the voxel size h is smaller than the mean inter-particle distance d. The distance d can be approximated by the expression (V/N)1/3, with N the number of primary molecules and V the volume over which they are generated. In our simulation case, N = 200 and V=(0.2/21)3 μm3,and we get d = 1.63 nm. We, therefore, selected an initial mesh of 1283 voxels, giving a voxel size of h = 1.5625 nm, which is smaller than the distance d. We then applied the hRDME approach to adapt the size of the mesh during the simulation. It started from the initial mesh and changed over time to coarser meshes of 643, 323, 163, 83, 43, 22, and one voxel.
Figure 2 shows the comparison of the time-dependent yield of species (number of molecules) as computed with the particle-based SBS model and the compartment-based model. A very good agreement was observed between the results obtained with both models. Table 2 shows the speed-up factor of the compartment-based model compared to the particle-based SBS model for different time scales covered by the simulations. The speed-up factor is defined as the ratio between the particle-based SBS and the compartment-based model simulation time. While simulations with end times less than 100 ns show a speed-up factor of one order of magnitude, we observed larger factors for longer timescales. The explanation is that, for timescales from 1 ns to 100 ns, the compartment-based model is performed in fine resolution meshes of 1283, 643, 323, and 163 voxels, which makes the compartment-based model less computationally efficient than at longer timescales (from 100 ns to 100 µs) where the system is transferred to coarser meshes. Moreover, at longer timescales, the particle-based SBS is much less efficient than the compartment-based model because it requires using small time-steps when the species reach the volume borders (boundary interactions).
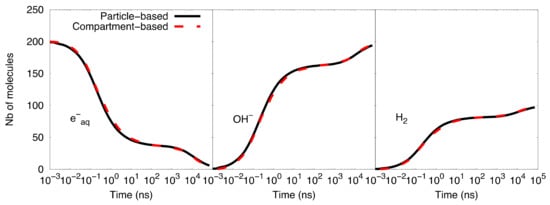
Figure 2. Compartment-based model for the simplified diffusion-reaction system compared with the particle-based SBS simulation.
Table 2. Speed-up factor of the compartment-based model compared to the particle-based SBS model for different simulation end times from 1 ns to 100 µs.
| End time | 1 ns | 10 ns | 100 ns | 1 µs | 10 µs | 100 µs |
| Speedup factor | 13 | 15.7 | 16.5 | 2.5 × 102 | 2.3 × 103 | 2.3 × 104 |
4. Full Water Radiolysis Simulation
For the third benchmark, we tested our full SBS-RDME model with a water radiolysis simulation. A water box of 0.2 × 0.2 × 0.2 µm was randomly irradiated on one face by a normal incident beam of 1 MeV electrons. The incident electrons were shot until the sum of all energy deposits in the volume led to an absorbed dose of 100 Gy (about 5 keV for the considered water volume). In this simulation, we used the physics list “G4EmDNAPhysics_option2” for the modeling of the physical stage. The microscopic sub-stage (see Figure 6) extended until 1 ns, at which point, we initiated the compartment-based model with a mesh of 323 voxels. We then used the hRDME approach to successively transfer species from the finer mesh to coarser meshes of 163, 83, 43, 23, and finally one voxel where the simulation volume is fully homogeneous.
The list of reactions and reaction rates considered in this work are shown in Table 3. It is worth noting that, in this work, these reactions are considered to be diffusion-controlled reactions where the products are created as soon as the reactants encounter each other.
Table 3. The reactions and reaction rates [13] used in this work that apply at ambient temperature (25 °C).
| Reaction | Reaction Rate (1010 M−1s−1) |
|
|---|---|---|
| 1 | H• + e−aq + H2O → OH− + H2 | 2.5 |
| 2 | H• + •OH → H2O | 1.55 |
| 3 | H• + H• → H2 | 0.503 |
| 4 | H2O2 + e−aq → OH− + •OH | 1.1 |
| 5 | H3O+ + e−aq → H• + H2O | 2.11 |
| 6 | H3O+ + OH− → 2H2O | 11.3 |
| 7 | •OH + e−aq → OH− | 2.95 |
| 8 | •OH + •OH → H2O2 | 0.55 |
| 9 | e−aq + e−aq + 2H2O → 2OH− + H2 | 0.636 |
Figure 3 shows the comparison of time-dependent G-values as computed by the particle-based SBS model of Geant4-DNA and our SBS-RDME model. Note that the comparison is considered from 1 ns when the compartment-based model is activated in the SBS-RDME model. A good agreement was observed for the entire time range between both models, thus, validating our SBS-RDME model implementation. Both SBS-RDME and particle-based SBS models showed that the system reached a steady-state at about 100 µs.
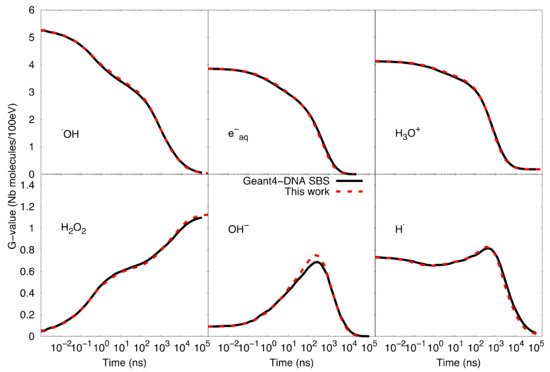
Figure 3. Comparison of time-dependent G-values as computed with the particle-based SBS model and the SBS-RDME model (this work) from 1 ns until 100 µs.
Figure 3 also shows a slight imbalance of neutrality of about 0.18 molecules per 100 eV observed in the G-value of H3O+. The explanation is that during the physical stage, some secondary electrons left the simulated volume as a result of ionizations that took place near the volume borders. These escaping electrons would not produce solvated electrons in the considered volume, while the corresponding ionized water molecules would dissociate in the volume and, therefore, create the slight imbalance of neutrality.
5. Materials and Methods
The main characteristic of our model is the combination of the SBS Brownian dynamics model already available in Geant4-DNA with the compartment-based model using the RDME (so-called “SBS-RDME model”) in water radiolysis simulations. Figure 6 illustrates the simulation scheme of this combination.
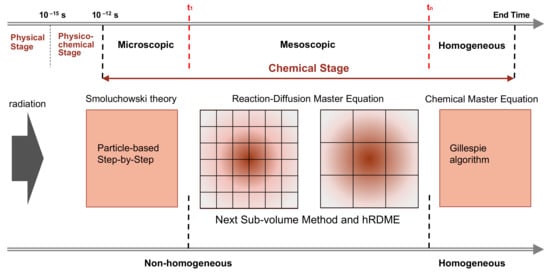
Figure 6. The simulation scheme of the combination of the particle-based SBS model with the compartment-based model that uses the RDME (SBS-RDME model).
We began by using Geant4-DNA [14][15][16][17][18][19][20] to model the physical and physico-chemical stage up to 1 ps. Then, the chemical stage was divided into three sub-stages: the microscopic, mesoscopic, and homogeneous sub-stages. The microscopic sub-stage started from the formation of species at the beginning of the chemical stage. As the spatial distribution of the early species (e−aq, H•, •OH, H3O+,…) was concentrated in very small volumes around the tracks, their evolutions largely depended on the species position. Therefore, at this sub-stage, we used the particle-based SBS method of Geant4-DNA to simulate the detailed trajectories of the individual species. Once the simulation reached a time t1, we stopped the particle-based SBS simulation and initiated a uniform 3D Cartesian mesh for the compartment-based model. This was the beginning of the mesoscopic sub-stage. The initial mesh resolution should be small and selected according to the spatial distribution of species at the end of the microscopic sub-stage. We then used the hRDME approach (see details in Section 4.2.2) to adapt the size of the voxels during the evolution of the system. The system used increasingly coarser meshes over time, to finally merge into one single voxel that covered the full simulation volume at time tn, when the homogeneous sub-stage started. During the homogeneous sub-stage, we used the CME stochastic process to sample only reactive events. The detail our implementation of the compartment-based model can be found in the original article.
6. Conclusions
In this work, we implemented, in Geant4-DNA, the compartment-based model combined with the SBS Brownian dynamics model already available in Geant4-DNA. We showed that the compartment-based model can reproduce the same species yield obtained by the particle-based SBS of Geant4-DNA but with 100 to 1000 times less computing time. Moreover, our new model can also extend the simulation timescale beyond the microsecond when the system has reached a steady-state. These advantages will allow us to study the production and evolution of reactive oxygen species generated under irradiation with different dose rate conditions, such as in FLASH and conventional radiotherapy.
In this work, we only considered a radiation-induced species system in a cubic water volume. The approach could be applied for more complicated systems, such as complex geometries including biological materials. This may be technically more difficult since we need to handle the two different representations (compartment-based and particle-based) in one simulation. We plan to work on such an extension in the future.
References
- Novakovskaya, Y.V. Theoretical estimation of the ionization potential of water in condensed phase. ii. superficial water layers. Prot. Met. 2007, 43, 22–33.
- Gauduel, Y.; Pommeret, S.; Antonetti, A. Femtosecond spec- troscopy of ultrafast reactions in aqueous media. J. Phys. Condens. Matter 1990, 2, SA171.
- Ogura, H.; Hamill, W.H. Positive hole migration in pulse-irradiated water and heavy water. J. Phys. Chem. 1973, 77, 2952–2954.
- Mozumder, A.; Magee, J.L. The early events of radiation chemistry. Int. J. Radiat. Phys. Chem. 1975, 7, 83–93.
- Clifford, P.; Green, N.J.B.; Pilling, M.J. Monte Carlo Simulation of diffusion and reaction in radiation-induced spurs. Comparison with analytic models. J. Phys. Chem. 1982, 86, 1322–1327.
- Karamitros, M.; Luan, S.; Bernal, M.; Allison, J.; Baldacchino, G.; Davidkova, M.; Francis, Z.; Friedland, W.; Ivantchenko, V.; Mantero, A.; et al. Diffusion-controlled reactions modeling in Geant4-DNA. J. Comput. Phys. 2014, 274, 841–882.
- Uehara, S.; Nikjoo, H. Monte Carlo Simulation of Water Radiolysis for Low-energy Charged Particles. J. Radiat. Res. 2006, 47, 69–81.
- Clifford, P.; Green, N.J.B.; Oldfield, M.J.; Pilling, M.J.; Pimblot, S.M. Stochastic models of multi-species kinetics in radiation-induced spurs. J. Chem. Soc. Faraday Trans. 1986, 82, 2673–2689.
- Frongillo, Y.; Goulet, T.; Fraser, M.; Cobut, V.; Patau, J.P.; Jay-Gerin, J.-P. Monte Carlo simulation of fast electron and proton tracks in liquid water—II. Nonhomogeneous chemistry. Radiat. Phys. Chem. 1998, 51, 245–254.
- Erban, R.; Chapman, S. Stochastic modelling of reaction-diffusion processes: Algorithms for bimolecular reactions. Phys. Biol. 2009, 6, 046001.
- Gillespie, D.T. Exact Stochastic Simulation of Coupled Chemical Reactions. J. Phys. Chem. 1977, 81, 2340–2361.
- Gillespie, D.T.; Hellander, A.; Petzold, L.R. Perspective: Stochastic algorithms for chemical kinetics. J. Chem. Phys. 2013, 138, 170901.
- Plante, I.; Devroye, L. Considerations for the independent reaction times and step-by-step methods for radiation chemistry simulations. Radiat. Phys. Chem. 2017, 139, 157–172.
- Incerti, S.; Baldacchino, G.; Bernal, M.A.; Capra, R.; Champion, C.; Francis, Z.; Guèye, P.; Mantero, A.; Mascialino, B.; Moretto, P.; et al. The Geant4-DNA project. Int. J. Model. Simul. Sci. Comput. 2010, 1, 157–178.
- Incerti, S.; Ivanchenko, A.; Karamitros, M.; Mantero, A.; Moretto, P.; Tran, H.N.; Mascialino, B.; Champion, C.; Ivanchenko, V.N.; Bernal, M.A.; et al. Comparison of Geant4 very low energy cross section models with experimental data in water. Med. Phys. 2010, 37, 4692–4708.
- Bernal, M.A.; Bordage, M.; Brown, J.; Davídková, M.; Delage, E.; El Bitar, Z.; Enger, S.; Francis, Z.; Guatelli, S.; Ivanchenko, V.; et al. Track structure modeling in liquid water: A review of the Geant4-DNA very low energy extension of the Geant4 Monte Carlo simulation toolkit. Phys. Medica 2015, 31, 861–874.
- Incerti, S.; Kyriakou, I.; Bernal, M.A.; Bordage, M.C.; Francis, Z.; Guatelli, S.; Ivanchenko, V.; Karamitros, M.; Lampe, N.; Lee, S.B.; et al. Geant4-DNA example applications for track structure simulations in liquid water: A report from the Geant4-DNA Project. Med. Phys. 2018, 45, e722–e739.
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. Geant4—a simulation toolkit. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2003, 506, 250–303.
- Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Dubois, P.A.; Asai, M.; Barrand, G.; Capra, R.; Chauvie, S.; Chytracek, R.; et al. Geant4 developments and applications. IEEE Trans. Nucl. Sci. 2006, 53, 270–278.
- Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barrand, G.; et al. Recent developments in GEANT4. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2016, 835, 186–225.
More
Information
Contributor
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
1.9K
Revisions:
2 times
(View History)
Update Date:
24 Jun 2021
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No




