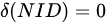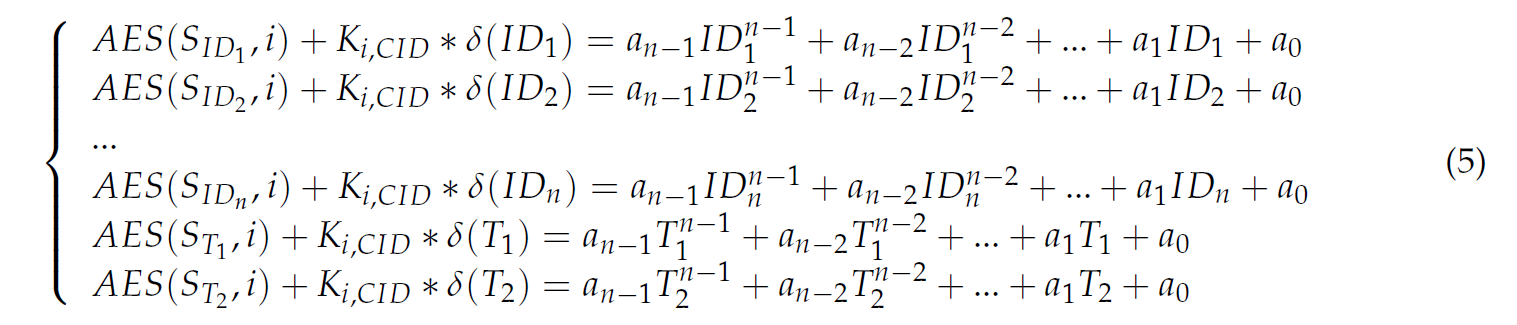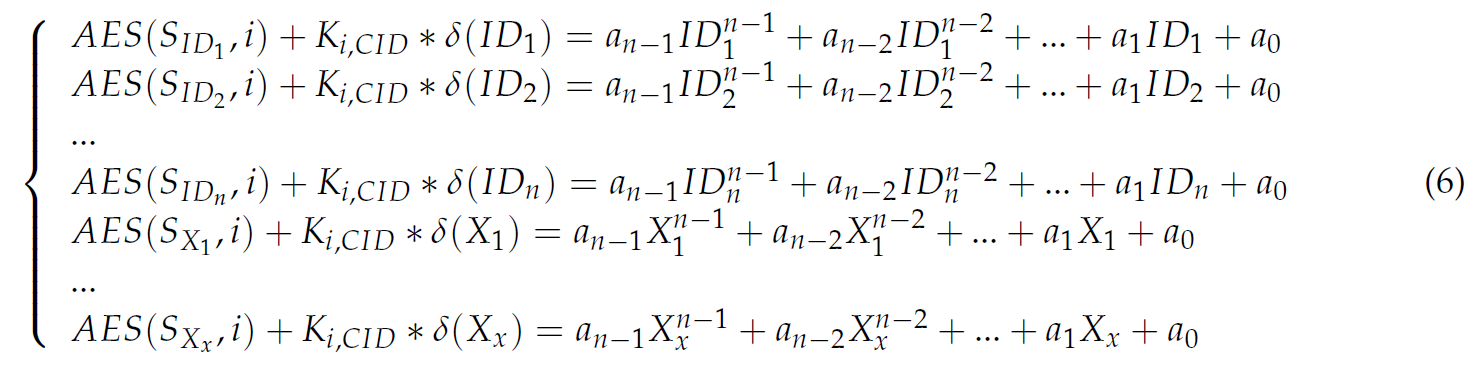1. Overall Design

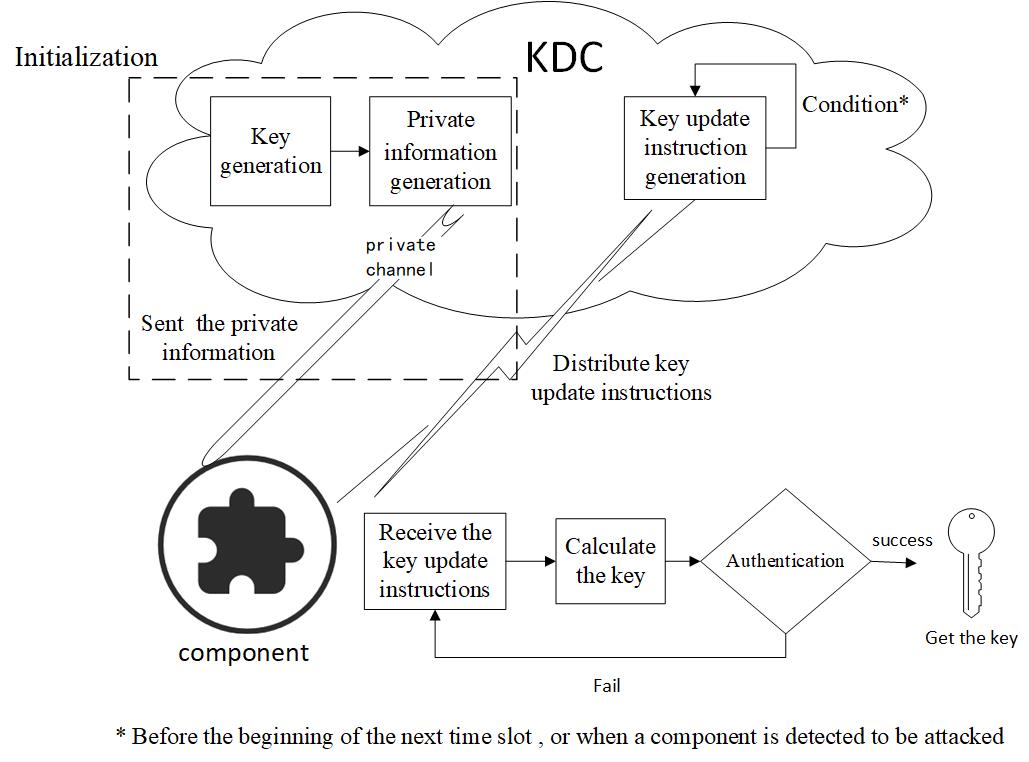
This entry proposes a security key establishment mechanism based on the high-order polynomial. It discusses the key management among the multiple smart components (such as sensors and actuators) on a single robot in the multi-robots network, and it is based on a symmetric key distribution algorithm. The key-center (or the cloud) sends the key in a time slot to the components by sending the coefficients of a polynomial. The components restore the coefficients to a polynomial and plug the private information themselves into the polynomial to obtain the key. The components are divided into multiple communication groups (or clusters) in the typical bus topological structure, according to the attribution of the components. The keys in a cluster are generated and distributed by the key center periodically.

At the beginning of a period, all keys in this period are generated by the key center and distributed to the components before each time slot begins. The process is presented as follows, and it is shown in Figure 1.

(1). At the beginning, the key center calculates the communication session key (K_1,CID, K_2,CID, ., K_N,CID) of a cluster in the N time slots, based on the cluster identification information CID, and saves them in the key center.

(2). The key center generates private information for each communication component in the cluster. The private information is sent to each component through a secure private channel at initialization. It is privately stored by each component, and is used to calculate the keys in the next few time slots.

(3). Before the beginning of the next time slot i, or when a component is detected to be attacked, the key center calculates the coefficients of a set of polynomials and generates a key update instruction, which is broadcast to components of a cluster.

(4). The key center broadcasts the ID information of the components which are attacked to all components in the key update instruction.

(5). After receiving the key update instruction, the component restores the polynomial and calculates the key according to the formula.

(6). After the calculation, the component uses the message authentication code to identify whether the received information is true and complete.

(7). The component updates the key based on the authentication result.

 2. Key Factor Initialization

On a smart robot, the communication components (such as sensors) communicate and cooperate closely with each other. Some other smart robots that have business relevance to the robot also communicate frequently with it. Therefore, all communication components on the smart robot form a communication group called cluster. In each cluster, a component that can communicate with all other components in the cluster is called the cluster head component. In general, the cluster head communicates with other components in the cluster using one or more full-duplex, half-duplex communication links such as UART, Ethernet, SPI, I2C, and CAN, and each cluster head communicates with cloud based on the IP network, such as GPRS, LTE, NBloT, LowPAN, etc. Therefore, to prevent the attackers from intercepting intra-cluster communication information through a shared medium or attacking the node itself, each component in the cluster needs to hold a common session key to encrypt and decrypt the communication information.

The communication session key between the intra-cluster communication components is distributed by the Key Distribution Center (KDC) located in the cloud, which greatly reduces computing resources for communication components with weak computing power. Each communication component holds a private and unique information identification value NID, and each cluster has a cluster identification CID. Before the start of communication for one cycle, the KDC generates a communication session key group {K_1,CID, K_2,CID, ., K_N,CID} for each normal communication component within the cluster CID, in the initial stage, the secret value S_NID required to calculate the session key is delivered to each communication component through the private channel.

In the initial stage, the key center uses the AES (Advanced Encryption Standard) algorithm to generate the communication session key of the components in the cluster. The AES algorithm is a highly efficient and high-security symmetric encryption algorithm. The algorithm encrypts the data with low computational cost and high security. Since the data encrypted by the key center do not need to be decrypted, the key center can save the key to ensure the privacy of the information. 

Before the key generation begins, the key center first generates a random number R through a reliable random source, which is stored as a root key by the key center and protects its privacy. For the key of the component within the cluster CID in the i time slot, the key center is generated as shown in Equation (1).

                 (1)

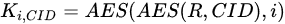
where i is the time slot number and CID is the unique identification number of the cluster.

The formula is used to generate the key of the component in the cluster, including the flag information of the cluster. The uniqueness of the flag information ensures the uniqueness of the key. Since only the private value of the generated key is stored in the key center, R, the storage cost of the key information is reduced, and the security of the key is greatly enhanced.

Definition 3.1 The private information of the component NID is S_NID, which is a ciphertext calculated by the AES algorithm by the key center according to the node ID of each component and the random number R generated by the key center. The generation of private information of the component NID is shown in Equation (2).

                                    (2)

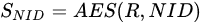
In the key factor initialization phase, the private information held by each component S_NID is written by the key center into the corresponding component through the protected channel according to its identification information NID in a controlled environment. Each component saves and protects its privacy in N time slots. This private information is used by each component for key calculations in subsequent N time slots.

3. Key Update Algorithm

3.1. Key Update Instruction

To improve the security of the key of communication session between components, the normal components in the cluster can respond to the attack in time. The key center will distribute the key update instruction to all the components in the cluster before the start of each time slot or when any component is detected to be attacked. The key update instruction sent by the key center to the components mainly carries the coefficient information of the key update polynomial F_i(X), the list of attacked components, and the list of random numbers. The key update polynomial is composed by the cluster key K_i,CID, the interference polynomial , and the identification information of each component. The formula is shown in Equation (3).

  (3)

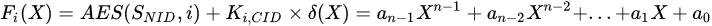
where S_NID is the private information held by each component, i is the time slot value, and {a₀, a₁, ., a_n-1} is the polynomial coefficient. When the number of normal components in the cluster m is greater than the number of components being attacked, then n = m + 2; otherwise, n = p + 3.

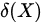
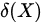
In the key updating, the key center introduces an interference polynomial in order to prevent the attacked components from getting the communication session key of the next time slot and excluding the interference of attacked components to the intra-cluster communication. The is
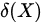
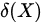
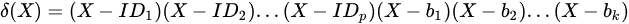
defined as Equation (4). The coefficients of consist of the identification information of the attacked components and some random numbers. The interference polynomial lists the identification information of the attacked components, so that the attacked components would not be able to obtain the key of the new time slot, even though they relive the key update instruction. When the number of attacked components p is less than the number of normal components m, the introduction of the random number list makes the highest index of the key update polynomial achieve the number m + 1. When the number of attacked components p is greater than the number of normal components m, the equation only introduces two random numbers b₁ and b₂, and the highest index of the key update polynomial is p + 2.

      (4)

where {ID₁, ID₂, ., ID_p } is the ID of the attacked components, p is the number of attacked components,
and {b₁, b₂, ., b_k} is a random number generated by a key source random source. When p < m, p + k = m + 1; otherwise, k = 2.

Equation (3) shows that the key update polynomial is determined by the coefficients {a₀, a₁, ., a_n-1}, and the index of the polynomial coefficient is n. The coefficient calculation of the key update polynomial is performed in the key center. When the number of normal components (m) in the cluster is greater than the number of attacked components (p), the IDs of all normal components in the cluster, the private information value corresponding to the component, and the anti-attack pairs (T₁, S_T1 ) and (T₂, S_T2 ), which are generated randomly, are brought into Equation (3) to get Equation (5). In the calculation of polynomial coefficient, the addition of random number pairs makes it impossible for the attacker to obtain the private information of all components, and the key of the next time slot cannot be calculated due to the existence of the random number, thereby improving the security of the key.

When the number of normal components (m) in the cluster is less than the number of the attacked components (p), the key center will automatically generate x pairs of anti-attack number (X_j, S_Xj ), so that m + x = p +2. The key center can bring the ID of all normal components and their corresponding private information values, together with the x pairs of anti-attack number randomly generated above, into Equation (3), obtaining the equation set shown in Equation (6).

Solving the equation set in a finite field, a set of coefficient vectors [a₀, a₁, ., a_n-1] can be obtained. The key center composes the coefficient vectors together with the identification information list of the attacked components and the random number list in the interference polynomial 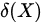to form a key update instruction, and then sends it to all communication components in the cluster by broadcast. It should be noted that the attacked components do not receive the key update instruction. 

3.2. Handling of Key Update Instructions

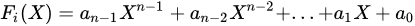
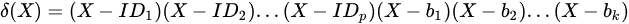
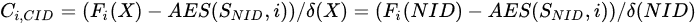
The process of a component receiving the key update instruction is shown in Algorithm 1. After receiving the key update instruction sent by the key center, the component takes out the coefficient information [a₀, a₁, ., a_n-1], which is carried in the instruction, to construct the key distribution polynomial . The ID list of the attacked components and the random number list which are published by the key center can construct the polynomial  . According to the formula shown in Equation (7), we can calculate the key C_i,CID, which is the session key of cluster CID in the next time slot.

   (7)

where i is the time slot number.

Each component takes its own node identifier NID, and the private information S_NID saved by the component itself, into Equation (7) to obtain the intra-cluster communication session key C_i,CID in the next slot. Since the attacked components have already been published by the key center, even though their own identification information and private information value are brought into Equation (7), they also cannot calculate the key value in the next time slot, due to the interference polynomial .