| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Yang Wang | + 2733 word(s) | 2733 | 2020-11-06 05:27:58 |
Video Upload Options
A modular multilevel converter (MMC) is an advanced voltage source converter applicable to a wide range of medium and high-voltage applications. It has competitive advantages such as quality output performance, high modularity, simple scalability, and low voltage and current rating demand for the power switches. The generalized configuration of a three-phase MMC is comprised of a DC terminal, an AC terminal, and a converting kernel involving three phase legs. Each leg/phase has two symmetric arms referred to as the upper arm and lower arm. The upper arm and lower arm contain a group of identical submodules connected in series together with a chock inductor to suppress high-frequency components in the arm current. The research interests of MMCs are primarily associated with the topologies, mathematical modeling, output voltage and current control, submodule balancing control, circulating current control, and modulation methods. And the incorporation of wideband gap (WBG) semiconductors are prospected to facilitate the MMC application with further advantages of high-voltage and high-power operations, low power losses, high efficiency, improved reliability, and reduced module size and cooling system.
1. Introduction
The modular multilevel converter (MMC), as a recently developed member of the multilevel converter family, was first proposed by Lesnicar and Marquardt in 2002 [1]. In 2010, this innovative converter was first commercially used by Siemens in San Francisco’s Trans bay project [2]. Since its first introduction, the MMC has gained considerable attention and development owing to its promising advantages such as excellent output performance, high modularity, simple scalability, and low voltage and current rating demand for the power switches [3][4]. These are clear advantages for the MMC over the traditional two-level and multilevel converters [5]. The MMC is particularly applicable to a wide range of medium and high-voltage power conversion systems, such as high-voltage direct current (HVDC) transmission systems [6][7], medium voltage motor drives [8][9], renewable energy systems [10][11], battery energy storage systems (BESS) [12][13], static synchronous compensator (STATCOM) [14][15], (hybrid) electrical vehicle chargers and drivers [16][17], and power interfacing applications [18][19].
The main purpose of this review paper is to present the current state of the art of the MMC technology and offer a better understanding of its operation and control. In this context, a detailed review is conducted associated with the main research issues regarding circuit topologies, mathematical modeling, control schemes, and modulation methods. The MMC circuit configuration is reviewed comprehensively from the perspective of the submodule and overall topologies. Despite limited DC fault tolerance [20][21], the half-bridge submodule (HBSM) is much preferred commercially among a variety of two-level and multilevel topologies considering its simple configuration and low cost. Advanced overall topologies are reported over the past years to meet application-oriented requirements. The MMC control methods are developed and reported with respect to the output voltage and current regulation [22], submodule balancing [23], and circulating current elimination [24] or injection [25]. Meanwhile, nonlinear and predictive controls [26] provide a solution to improve the MMC dynamic response instead of using a conventional proportional integral (PI) regulator or resonant controller. The modulation techniques of the power converter [27] directly affect the output value and output quality on power semiconductors. Numerous studies have been carried out to improve the modulation methods and are considered in this review. The emerging WBG technology [28] leads to a revolution in power electronics, which is prospected with power losses estimation using different modulation techniques in the MMC application.
2. MMC Topologies
The generalized configuration of a three-phase MMC is comprised of a DC terminal, an AC terminal, and a converting kernel involving three phase legs, as shown in Figure 1. Each leg/phase has two symmetric arms referred to as the upper arm and lower arm. The upper arm and lower arm contain a group of identical submodules connected in series together with a chock inductor to suppress high-frequency components in the arm current. An MMC can achieve bidirectional power conversion.
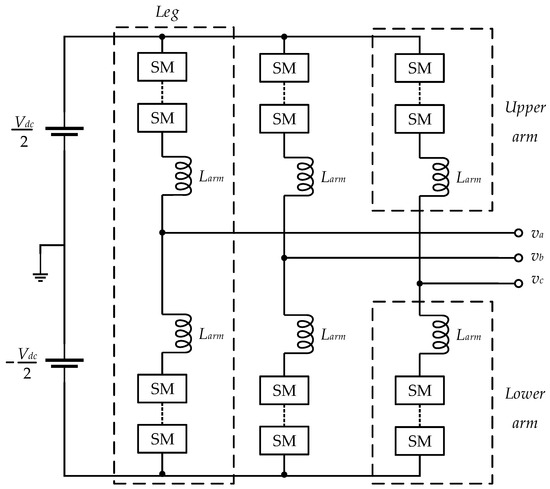
Figure 1. Generalized configuration of a three-phase modular multilevel converter (MMC).
The submodule is the fundamental component of an MMC. According to the output voltage level, these submodules can be classified into two categories: two-level submodule topologies with a single source and multilevel submodule topologies with multiple sources. Among all the submodule topologies, the half-bridge submodule (HBSM) [1] is the most popular configuration thanks to its simple structure together with a low system cost.
In terms of MMC overall topologies, the phase-leg or arm structure is one of the research points to improve the performance of MMCs. The hybrid arm/leg architecture is a key factor to trade off the system cost, power losses, and DC fault blocking capacity. Hybrid MMCs usually contain two different submodules. A symmetric hybrid MMC in [29] is based on HBSMs and FBSMs. A new family of MMC referred to as bifurcate MMCs is investigated in [30][31]. Du et al. propose a passive cross-connected MMC (PC-MMC) [9] and an active cross-connected MMC (AC-MMC) [32]. The difference is that the flying capacitor in the PC-MMC is replaced by a series of additional submodules in the AC-MMC.
According to the connection schemes of the MMC arms, the overall architectures can be classified as star-configured MMCs and delta-configured MMCs [33][34]. They can be further split into single-star, single-delta, double-star, double-delta, and triple-star based on star and delta count. The configuration circuits are shown in Figure 2. A triple-star MMC [35] is also well-known as a “modular multilevel matrix converter” (M3C) [36][37]. Figure 2d,e are the two same presentations for triple-star MMC or M3C. In recent years, researchers developed a new topology for MMC referred to hexagonal MMC or Hexverter [38]. The Hexverter consists of six arms connected in a hexagonal circuit, and each arm is alternatively connected to one phase of two three-phase AC networks, as shown in Figure 2f. The Hexverter has limited reactive power provision capability at some operation points, together with injected common-mode voltage, which is not expected in some applications such as motor drives. Therefore, another hexagonal topology called Hex-Y [39][40] is proposed based on the Hexverter. Except for the retaining hexagon circuit, three star-connected branches are added within the hexagon, as shown in Figure 2g.
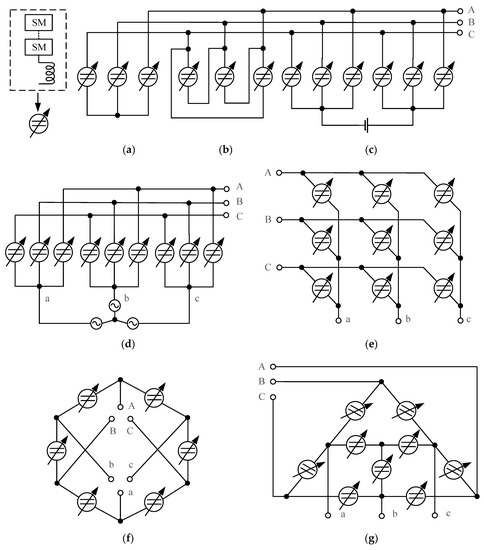
Figure 2. MMC arm configurations: (a) Single-star MMC; (b) Single-delta MMC; (c) Double-star MMC; (d) Triple-star MMC; (e) M3C; (f) Hexverter; (g) Hex-Y.
3. MMC Control Strategies
The MMC control strategies enable its high performance associated with superior safety, reliability, and efficiency. The control is challenging and sophisticated as involving substantial submodules and multiple control objectives related to the output voltage and current control, submodule voltage or SoC balancing control, and circulating current control.
The submodule balancing control in the MMC mainly involves leg/arm voltage balancing control, submodule capacitor voltage balancing control, or SoC balancing control if based on a battery submodule. Various submodule balancing schemes have been discussed and presented in the literature. These approaches are mainly based on individual voltage/SoC control or a sorting algorithm to equilibrate between submodules. Generally, when a small number of submodules are explored in the converter, the individual voltage/SoC control can be applied to realize the individual voltage/SoC regulation; otherwise, the sorting algorithm is preferred in the application with increased submodules by selecting the inserted/bypassed submodules in order of priority [4]. The individual balancing control and sorting control are also well-known as distributed balancing control and centralized balancing control [5][41].
The voltage difference between the upper and lower arms of the MMC legs results in the circulating current. The circulating current has little influence on the output voltages and currents at the AC side. However, it distorts the arm current, leading to extra power losses, a higher rating of devices, and submodule voltage ripples [42]. Therefore, the circulating current is expected to be eliminated. The arm inductors can suppress the circulating current to some extent [43]. Furthermore, the elimination controller is required to be employed. Since the circulating current is dominated by even-order harmonic components, especially second-order harmonics, the control objective of the elimination controller mainly focuses on the elimination of second-order harmonics [44]. The circulating current elimination approaches are based on decoupling control in the rotating dq-frame or resonant control in the stationary abc-frame. In terms of decoupling control, the second-order circulating current is converted into a d-axis and q-axis as DC components, which can be controlled easily and independently by PI regulators[45][46]. In the case of unbalanced conditions where the circulating currents have positive, negative, and zero sequence components, the repetitive controller [47][48] can be applied to regulate multiple circulating current harmonics. Compared to decoupling methods, the proportional resonant controller has some advantages under unbalanced conditions with an easier implementation of multiple resonant controllers to eliminate a wider bandwidth of circulating current harmonics [49][50].
The MMC as a switching converter is a nonlinear system associated with multiple coupled variables. The conventional control methods are easy to implement in digital controllers by using linear techniques. However, these methods have a limitation on the dynamic response in terms of multiple control objectives such as AC current and voltage, leg/arm voltage, and circulating currents. To achieve simultaneous control and dynamic response, nonlinear and predictive control strategies are promising alternatives for MMC applications. Model predictive control (MPC), is a preferable choice for power converters as it is a nonlinear control method. The MPC method can deal with multiple constraints in a single cost function and provide fast dynamic response and robustness against parameter variation and external disturbance. The finite control set MPC (FCS-MPC), also known as direct MPC, is a popular predictive approach used in MMC control. One disadvantage of the FSC-MPC is the computational burden to obtain the optimal switching states, which worsens with increasing voltage levels. To deal with this issue, a fast FCS control scheme is investigated. Fast FCS-MPC [51], also known as indirect MPC, remains the submodule balancing strategy along with the predictive control. The predictive control is employed as the primary controller to control the output and circulating currents. Meanwhile, the submodule balancing strategy is applied as the secondary controller to equalize the submodule voltages or SoCs within the arm. The computational effort of the indirect FCS-MPC is minimized to a large extent, as only N+1 switching states are required to be evaluated for the optimal cost function.
4. MMC Modulation Techniques
Various pulse width modulation (PWM) techniques have been developed to generate a desired output voltage for the MMC. These modulation techniques, depending on the switching frequency, can be classified as high switching frequency PWM (HSF-PWM), low switching frequency (LSF-PWM), and fundamental switching frequency (FSF-PWM) modulation scenarios [3][5]. The semiconductor switching losses increase with the switching frequency. As a result, the high switching frequency method is generally utilized when a small number of submodules are employed, whereas low switching frequency and fundamental switching frequency schemes are preferred when substantial submodules are involved [4].
Carrier-based PWM is a typical HSF-PWM method in which, for multilevel converters, the modulation reference of each phase is compared with multiple carrier waveforms to create the gating signals [27]. Triangular or sawtooth waveforms are prevalently applied as the compared carrier signals. Carrier-based modulation schemes, based on the arrangement of multiple carriers, are categorically divided as phase-shifted carrier-based (PSC-PWM) and level-shifted carrier-based (LSC-PWM) techniques [52].
The switching frequency of space vector modulation (SVM) falls into the category of the LSF-PWM scheme. It is advantageous to select the switching vectors and arrange the switching sequences with more freedom in SVM-PWM. SVM-PWM has demonstrated good performance with superior harmonic features and DC-link utilization in the two-level converter [53]. However, when it comes to multilevel modulation, the SVM-PWM algorithm is challenging to implement with the significantly increased computational burden and complexity [1]. Another low switching frequency modulation approach referred to sampled average modulation (SAM) has a similar process to SVM-PWM but with less computation complexity and simple implementation to multilevel converters with any number of submodules [54]. In SAM-PWM, the command voltage is produced by averaging the two nearest voltage levels and avoiding zero vectors in each sampling interval.
In terms of fundamental switching frequency modulation, a quite popular method is nearest level modulation (NLM) [55][56]. In this approach, the switching states and dwell time are directly derived from the command voltage eliminating the use of carrier signals. It is easy and practical to implement, especially in the case of MMC involving a large number of submodules. Selective harmonic elimination (SHE) also belongs to the category of FSF-PWM. SHE-PWM [57] can provide a high performance of output voltages. However, this method is difficult to implement due to the heavy calculation of substantial switching angles with multilevel voltages. An overview and comparison of different modulation techniques regarding modulation categories, switching frequency, application with the employed number of submodules, output harmonic performance, and implementation effort are presented in Table 2.
Table 2. Pulse width modulation techniques.
5. Power Losses and WBG Technology
Wideband gap semiconductors, made on silicon carbide (SiC) and gallium nitride (GaN) provide advantages of increased energy efficiency, high power density, and cooling density thanks to improved electrical and thermal conductivities [58][59]. WBG transistors are expected to occupy a wide range of power conversion applications which are dominated by the traditional Si-based power devices over the past decades. Power loss calculation is critical for thermal management and cooling in terms of applications with high power density. Power losses for semiconductors consist of conduction and switching losses. The low on-state resistance of WBG power devices contributes to a reduced conduction loss compared with Si-based modules.
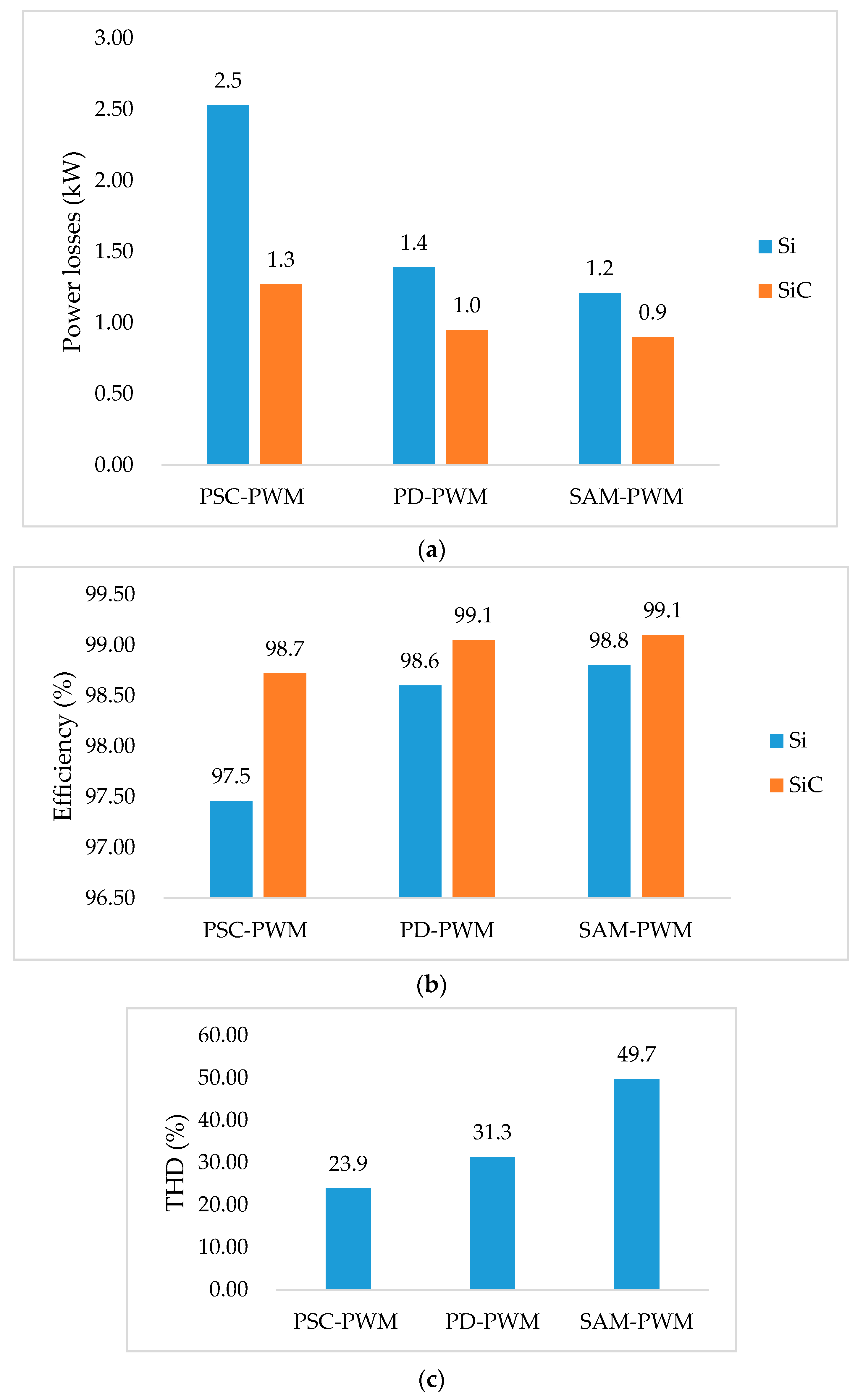
In order to assess the thermal performance of conventional Si-based semiconductors and WBG switching modules modulated by different modulation techniques for the MMC, the power losses calculation model is carried out with the simulation model in MATLAB. The simulation results are demonstrated graphically as in Figure 3 illustrates the comparative performance based on semiconductor power losses, MMC efficiency, and output voltage THD by using different modulation methods. From Figure 3a,b, it is noticed that SiC modules, compared to Si devices, yield lower power losses and higher power efficiency for all the three modulation techniques. It is also indicated that the PSC-PWM has higher power losses following with the PD-PWM and SAM-PWM for both Si and SiC switches in Figure 3a, which leads to a reduced MMC efficiency, as shown in Figure 3b. In spite of lower performance in power losses and efficiency, Figure 3c manifests that PSC-PWM is prominent in providing good voltage quality with lower THD compared to the other two methods. The comparison of performance indicates that the differences in the material properties of switching devices lead to the fact that the WBG components have superior performance regarding reduced power losses and higher power efficiency. The advantages of WBG power transistors can further substantially reduce the size of whole power conversion systems with strong robustness. It is expectable that WBG power switches will play a prominent role together with the MMC in the power conversion applications in the near future.
Figure 3. Comparative performance of using Si and SiC semiconductors with different modulation methods and load (100 kW) and input voltage per MMC HBSM (300 V): (a) Semiconductor power losses; (b) MMC efficiency; (c) Output voltage total harmonic distortion (THD).
6. Conclusions
The MMC is expected to be a preferable choice in the medium and high-voltage power applications with intrinsic advantages such as scalable multilevel output voltage, low harmonic content of output voltage and output current, modular and flexible design, improved efficiency, and redundancy. This paper reviews the MMC with respect to the submodule and overall topologies, control methods, modulation techniques, and power losses with the incorporation of WBG technology. As an application-oriented topology, it is predictable that the MMC will be guided to be more customized and well-adapted in the specific application area in terms of power transmission and quality improvement. With respect to MMC control, the output voltage and current control under different grid conditions, submodule balancing control, and circulating current control are discussed. The challenging issues include the submodule balancing control, circulating current control, multiple variables’ simultaneous control, and the complexity of consequent control. Nonlinear and predictive control strategies could be promising alternatives compared to conventional control methods. Modulation techniques are reviewed and classified according to switching frequency with decent application area and implementation effort. Power losses are investigated with the incorporation of WBG technology by using different modulation methods. The comparison of performance indicates that PSC-PWM has better output performance while generating higher power losses compared to PD-PWM and SAM-PWM, and the WBG semiconductors have superior performance regarding reduced power losses and higher power efficiency. The incorporation of WBG technology will facilitate the MMC application with further advantages of high-voltage and high-power operations, low power losses, high efficiency, improved reliability, and reduced module size and cooling system.
References
- Lesnicar, A.; Marquardt, R. An innovative modular multilevel converter topology suitable for a wide power range. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings,; IEEE: Bologna, Italy, Italy, 2003; Vol. 3, pp. 272–277.
- Friedrich, K. Modern HVDC PLUS application of VSC in Modular Multilevel Converter topology. In Proceedings of the 2010 IEEE International Symposium on Industrial Electronics; IEEE, 2010; pp. 3807–3810.
- Du, S.; Dekka, A.; Wu, B.; Zargari, N. Modular Multilevel Converters: Analysis, Control, and Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2017; ISBN 9781119367291.
- Martinez-Rodrigo, F.; Ramirez, D.; Rey-Boue, A.B.; De Pablo, S.; Herrero-De Lucas, L.C. Modular multilevel converters: Control and applications. Energies 2017, 10, doi:10.3390/en10111709.
- Raju, M.N.; Sreedevi, J.; Mandi, R.P.; Meera, K.S. Modular multilevel converters technology: A comprehensive study on its topologies, modelling, control and applications. IET Power Electron. 2019, 12, 149–169, doi:10.1049/iet-pel.2018.5734.
- Lyu, D.; Sun, Y.; Teixeira, C.A.; Holmes, D.G.; McGrath, B.P.; Wang, Q. A Novel Modular Multilevel Converter with Coupled-inductor Semi-bridge Submodules. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE); IEEE, 2019; Vol. 40, pp. 6860–6867.
- Alyami, H.; Mohamed, Y. Review and development of MMC employed in VSC-HVDC systems. In Proceedings of the 2017 IEEE 30th Canadian Conference on Electrical and Computer Engineering (CCECE); IEEE, 2017; pp. 1–6.
- Chakraborty, S.; Vu, H.-N.; Hasan, M.M.; Tran, D.-D.; Baghdadi, M. El; Hegazy, O. DC-DC Converter Topologies for Electric Vehicles, Plug-in Hybrid Electric Vehicles and Fast Charging Stations: State of the Art and Future Trends. Energies 2019, 12, 1569, doi:10.3390/en12081569.
- Du, S.; Wu, B.; Zargari, N.R.; Cheng, Z. A Flying-Capacitor Modular Multilevel Converter for Medium-Voltage Motor Drive. IEEE Trans. Power Electron. 2017, 32, 2081–2089, doi:10.1109/TPEL.2016.2565510.
- Verdugo, C.; Candela, J.I.; Blaabjerg, F.; Rodriguez, P. Three-Phase Isolated Multimodular Converter in Renewable Energy Distribution Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 854–865, doi:10.1109/JESTPE.2019.2895465.
- Bayat, H.; Yazdani, A. A Hybrid MMC-Based Photovoltaic and Battery Energy Storage System. IEEE Power Energy Technol. Syst. J. 2019, 6, 32–40, doi:10.1109/JPETS.2019.2892418.
- Hillers, A.; Biela, J. Fault-tolerant operation of the modular multilevel converter in an energy storage system based on split batteries. In Proceedings of the 2014 16th European Conference on Power Electronics and Applications; IEEE, 2014; pp. 1–8.
- Sangiri, J.B.; Raiesh, V.; Chattopadhyay, S.K.; Chakraborty, C. Modular Multilevel Converter for Multifunctional Battery Management System of Electric Vehicle. In Proceedings of the IECON 2018 - 44th Annual Conference of the IEEE Industrial Electronics Society; IEEE, 2018; pp. 1333–1338.
- Tianqi, L.; Youyin, W.; Zhanjun, L.; Meijun, L.; Weimao, X.; Yunche, S.; Zhijian, C.; Na, Z. Reactive Power Compensation and Control Strategy for MMC-STATCOM Doubly-Fed Wind Farm. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies - Asia (ISGT Asia); IEEE, 2019; pp. 3537–3542.
- Zhang, Y.; Chen, X.; Sun, J. Sequence Impedance Modeling and Analysis of MMC in Single-Star Configuration. IEEE Trans. Power Electron. 2020, 35, 334–346, doi:10.1109/TPEL.2019.2911998.
- Mao, M.; Ding, Y.; Chang, L.; Hatziargyriou, N.D.; Chen, Q.; Tao, T.; Li, Y. Multi-Objective Power Management for EV Fleet With MMC-Based Integration Into Smart Grid. IEEE Trans. Smart Grid 2019, 10, 1428–1439, doi:10.1109/TSG.2017.2766363.
- Pizzo, A. Del; Coppola, M.; Spina, I. Current waveforms distribution among electrochemical cells of Modular Multilevel Converters in Battery Electric Vehicles. In Proceedings of the 2018 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC); IEEE, 2018; pp. 1–4.
- Mahmoud, A.A.; Hafez, A.A.; Yousef, A.M. Modular Multilevel Converters for Renewable Energies Interfacing: Comparative review. In Proceedings of the 2019 IEEE Conference on Power Electronics and Renewable Energy (CPERE); IEEE, 2019; pp. 397–406.
- Wang, S.; Ahmed, K.H.; Adam, G.P.; Massoud, A.M.; Williams, B.W. A Novel Converter Station Structure for Improving Multiterminal HVDC System Resiliency Against AC and DC Faults. IEEE Trans. Ind. Electron. 2020, 67, 4270–4280, doi:10.1109/TIE.2019.2926036.
- Li, X.; Song, Q.; Liu, W.; Rao, H.; Xu, S.; Li, L. Protection of Nonpermanent Faults on DC Overhead Lines in MMC-Based HVDC Systems. IEEE Trans. Power Deliv. 2013, 28, 483–490, doi:10.1109/TPWRD.2012.2226249.
- Xu, J.; Zhao, P.; Zhao, C. Reliability Analysis and Redundancy Configuration of MMC With Hybrid Submodule Topologies. IEEE Trans. Power Electron. 2016, 31, 2720–2729, doi:10.1109/TPEL.2015.2444877.
- Wei, J. Review of Current Control Strategies in Modular Multilevel Converter, Norwegian University of Science and Technology, 2016.
- Kumar, Y.S.; Poddar, G. Balanced Submodule Operation of Modular Multilevel Converter-Based Induction Motor Drive for Wide-Speed Range. IEEE Trans. Power Electron. 2020, 35, 3918–3927, doi:10.1109/TPEL.2019.2938096.
- Xu, Y.; Xu, Z.; Zhang, Z.; Xiao, H. A Novel Circulating Current Controller for MMC Capacitor Voltage Fluctuation Suppression. IEEE Access 2019, 7, 120141–120151, doi:10.1109/ACCESS.2019.2933220.
- Li, B.; Xu, Z.; Shi, S.; Xu, D.; Wang, W. Comparative Study of the Active and Passive Circulating Current Suppression Methods for Modular Multilevel Converters. IEEE Trans. Power Electron. 2018, 33, 1878–1883, doi:10.1109/TPEL.2017.2737541.
- Perez, M.A.; Rodriguez, J.; Fuentes, E.J.; Kammerer, F. Predictive Control of AC–AC Modular Multilevel Converters. IEEE Trans. Ind. Electron. 2012, 59, 2832–2839, doi:10.1109/TIE.2011.2159349.
- Marquez, A.; Leon, J.I.; Vazquez, S.; Franquelo, L.G.; Perez, M. A comprehensive comparison of modulation methods for MMC converters. In Proceedings of the IECON 2017 - 43rd Annual Conference of the IEEE Industrial Electronics Society; IEEE, 2017; Vol. 2017-Janua, pp. 4459–4464.
- Shenai, K. Future Prospects of Widebandgap (WBG) Semiconductor Power Switching Devices. IEEE Trans. Electron Devices 2015, 62, 248–257, doi:10.1109/TED.2014.2360641.
- Cai, Y.; Wen, M.; Chen, Y.; Shi, Y.; Qin, Y. Low DC Voltage Control Strategy of Bipolar LCC-MMC Hybrid HVDC Transmission System. In Proceedings of the 2017 2nd International Conference on Power and Renewable Energy (ICPRE); IEEE, 2017; pp. 166–171.
- Shi, G.; Chang, Y.; Cai, X.; Zhang, J. Bifurcate Modular Multilevel Converter for Low-modulation-ratio Applications. IET Power Electron. 2016, 9, 145–154, doi:10.1049/iet-pel.2015.0387.
- Chang, Y.; Cai, X. A New Family of Modular Multilevel Converters. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia); IEEE, 2016; Vol. 1, pp. 3483–3488.
- Du, S.; Wu, B.; Tian, K.; Zargari, N.; Cheng, Z. An Active Cross-Connected Modular Multilevel Converter (AC-MMC) for Medium-voltage Motor Drive. IEEE Trans. Ind. Electron. 2016, 63, 1–1, doi:10.1109/TIE.2016.2547875.
- Priya, M.; Ponnambalam, P.; Muralikumar, K. Modular-multilevel Converter Topologies and Applications – a Review. IET Power Electron. 2019, 12, 170–183, doi:10.1049/iet-pel.2018.5301.
- Madichetty, S.; Abhijit, D.; Jinka, S. A Survey and Experimental Verification of Modular Multilevel Converters. Int. J. Power Electron. Drive Syst. 2014, 4, 363–375, doi:10.11591/ijpeds.v4i3.5914.
- Kawamura, W.; Hagiwara, M.; Akagi, H. Control and Experiment of a Modular Multilevel Cascade Converter Based on Triple-Star Bridge Cells. IEEE Trans. Ind. Appl. 2014, 50, 3536–3548, doi:10.1109/TIA.2014.2311759.
- Karwatzki, D.; Mertens, A. Control Approach for a Class of Modular Multilevel Converter Topologies. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE); IEEE, 2016; pp. 1–9.
- Kammerer, F.; Kolb, J.; Braun, M. Fully Decoupled Current Control and Energy Balancing of The Modular Multilevel Matrix Converter. In Proceedings of the 2012 15th International Power Electronics and Motion Control Conference (EPE/PEMC); IEEE, 2012; p. LS2a.3-1-LS2a.3-8.
- Baruschka, L.; Mertens, A. A New 3-phase AC/AC Modular Multilevel Converter with Six Branches in Hexagonal Configuration. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition; IEEE, 2011; pp. 4005–4012.
- Blaszczyk, P. Hex-Y - A New Modular Multilevel Converter Topology for a Direct AC-AC Power Conversion. In Proceedings of the 2018 20th European Conference on Power Electronics and Applications (EPE’18 ECCE Europe); IEEE: Riga, Latvia, 2018; p. P.1-P.10.
- Blaszczyk, P. Low Frequency Mode Operation for Direct ac-ac Modular Multilevel Converter Systems. A Comparison of M3C and Hex-Y Topology. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE ’19 ECCE Europe); IEEE: Genova, Italy, 2019; p. P.1-P.10.
- Deng, F.; Lu, Y.; Liu, C.; Heng, Q.; Yu, Q.; Zhao, J. Overview on Submodule Topologies, Modeling, Modulation, Control Schemes, Fault Diagnosis, and Tolerant Control Strategies of Modular Multilevel Converters. Chinese J. Electr. Eng. 2020, 6, 1–21, doi:10.23919/CJEE.2020.000001.
- Wei, J.; Acharya, A.B.; Norum, L.; Bauer, P. Comparison of Current Control Strategies in Modular Multilevel Converter. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018 -ECCE Asia); IEEE, 2018; pp. 2630–2637.
- Li, Y.; Wang, F. Arm Inductance Selection Principle for Modular Multilevel Converters with Circulating Current Suppressing Control. In Proceedings of the 2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC); IEEE, 2013; pp. 1321–1325.
- Agelidis, V.G.; Pou, J.; Ceballos, S.; Darus, R.; Konstantinou, G. Controllers for Eliminating the ac Components in the Circulating Current of Modular Multilevel Converters. IET Power Electron. 2016, 9, 1–8, doi:10.1049/iet-pel.2014.0930.
- Qingrui Tu; Zheng Xu; Lie Xu Reduced Switching-Frequency Modulation and Circulating Current Suppression for Modular Multilevel Converters. IEEE Trans. Power Deliv. 2011, 26, 2009–2017, doi:10.1109/TPWRD.2011.2115258.
- Bahrani, B.; Debnath, S.; Saeedifard, M. Circulating Current Suppression of the Modular Multilevel Converter in a Double-Frequency Rotating Reference Frame. IEEE Trans. Power Electron. 2016, 31, 783–792, doi:10.1109/TPEL.2015.2405062.
- He, L.; Zhang, K.; Xiong, J.; Fan, S. A Repetitive Control Scheme for Harmonic Suppression of Circulating Current in Modular Multilevel Converters. IEEE Trans. Power Electron. 2015, 30, 471–481, doi:10.1109/TPEL.2014.2304978.
- Zhang, M.; Huang, L.; Yao, W.; Lu, Z. Circulating Harmonic Current Elimination of a CPS-PWM-Based Modular Multilevel Converter With a Plug-In Repetitive Controller. IEEE Trans. Power Electron. 2014, 29, 2083–2097, doi:10.1109/TPEL.2013.2269140.
- Li, S.; Wang, X.; Yao, Z.; Li, T.; Peng, Z. Circulating Current Suppressing Strategy for MMC-HVDC Based on Nonideal Proportional Resonant Controllers Under Unbalanced Grid Conditions. IEEE Trans. Power Electron. 2015, 30, 387–397, doi:10.1109/TPEL.2014.2329059.
- Ma, Y.; Fan, L. Circulating current and DC current ripple control in MMC under unbalanced grid voltage. In Proceedings of the 2015 North American Power Symposium (NAPS); IEEE, 2015; pp. 1–6.
- Vatani, M.; Bahrani, B.; Saeedifard, M.; Hovd, M. Indirect Finite Control Set Model Predictive Control of Modular Multilevel Converters. IEEE Trans. Smart Grid 2015, 6, 1520–1529, doi:10.1109/TSG.2014.2377112.
- McGrath, B.P.; Holmes, D.G. Multicarrier PWM Strategies for Multilevel Inverters. IEEE Trans. Ind. Electron. 2002, 49, 858–867, doi:10.1109/TIE.2002.801073.
- Pinheiro, H.; Botteron, F.; Rech, C.; Schuch, L.; Camargo, R.F.; Hey, H.L.; Grundling, H.A.; Pinheiro, J.R. Space Vector Modulation for Voltage-Source Inverters: A Unified Approach. In Proceedings of the IEEE 2002 28th Annual Conference of the Industrial Electronics Society. IECON 02; IEEE, 2002; Vol. 1, pp. 23–29.
- Dekka, A.; Wu, B.; Zargari, N.R. A Novel Modulation Scheme and Voltage Balancing Algorithm for Modular Multilevel Converter. IEEE Trans. Ind. Appl. 2016, 52, 432–443, doi:10.1109/TIA.2015.2477481.
- Nguyen, M.H.; Kwak, S. Nearest-Level Control Method With Improved Output Quality for Modular Multilevel Converters. IEEE Access 2020, 8, 110237–110250, doi:10.1109/ACCESS.2020.3001587.
- Meshram, P.M.; Borghate, V.B. A Simplified Nearest Level Control (NLC) Voltage Balancing Method for Modular Multilevel Converter (MMC). IEEE Trans. Power Electron. 2015, 30, 450–462, doi:10.1109/TPEL.2014.2317705.
- Ke Shen; Dan Zhao; Jun Mei; Tolbert, L.M.; Jianze Wang; Mingfei Ban; Yanchao Ji; Xingguo Cai Elimination of Harmonics in a Modular Multilevel Converter Using Particle Swarm Optimization-Based Staircase Modulation Strategy. IEEE Trans. Ind. Electron. 2014, 61, 5311–5322, doi:10.1109/TIE.2013.2297301.
- Shenai, K. Wide Bandgap (WBG) Semiconductor Power Converters for DC Microgrid Applications. In Proceedings of the 2015 IEEE First International Conference on DC Microgrids (ICDCM); IEEE, 2015; pp. 263–268.
- Shenai, K. Power Electronic Module: Enabling the 21st-century energy economy. IEEE Power Electron. Mag. 2014, 1, 27–32, doi:10.1109/MPEL.2014.2330459.