1000/1000
Hot
Most Recent

Interstitial light elements play an important role in magnetic materials. Especially, Mn-based compounds with interstitial atoms are important for the easy fabrication of highly functional magnetic devices.
Some crystal structures possess interstitial crystallographic sites, which light elements such as hydrogen, boron, carbon, nitrogen, and oxygen atoms can occupy. There is a rather long history of metallurgical, physical, and chemical research studies on interstitial atoms [1][2]. In past years, domain control of ferromagnets has been studied [1]. Since the 1980s, interstitial atoms have attracted intense attention related to the improvement of magnetic properties of rare-earth Fe and Co-based permanent magnets [2][3][4][5][6].
Interstitial atoms have two major roles—influencing the stability of the crystal structure and in the modification or change in magnetic properties. In the former case, small amounts of interstitial light elements are required to stabilize the desired crystal structure; compounds without interstitial atoms would not exist in thermal equilibrium. In the latter case, interstitial atoms affect the crystal structure parameters, such as the interatomic distances between magnetic atoms or the orbital hybridization between magnetic and interstitial atoms, consequently meaning the magnetic ordering temperature, the magnetic moment, the magnetic structure, and other factors can be altered.
The most well-studied platforms for interstitial atoms are rare-earth Fe-based permanent magnets. The improvements of the magnetic properties have mainly been achieved through the addition of light elements such as boron, carbon, and nitrogen atoms. The Bethe–Slater curve is one of the criteria needed to understand whether metal 3d transition elements of Cr, Mn, Fe, Co, and Ni possess ferromagnetic (FM) or antiferromagnetic (AFM) states (see Figure 1) [7][8][9][10]. This curve exhibits the exchange coupling as a function of the interatomic distance. Fe falls in the FM region near to the border between FM and AFM states. Therefore, in Fe-based compounds, a shorter Fe–Fe distance (shrinkage of the unit cell volume) favors an AFM state, while a longer Fe–Fe distance (an expansion of the unit cell volume) favors the FM state [11][12][13]. With increasing Fe–Fe distance, smaller overlapping of 3d wave functions makes the 3d band narrower, which leads to the FM state, and in most cases the Curie temperature TC is enhanced.
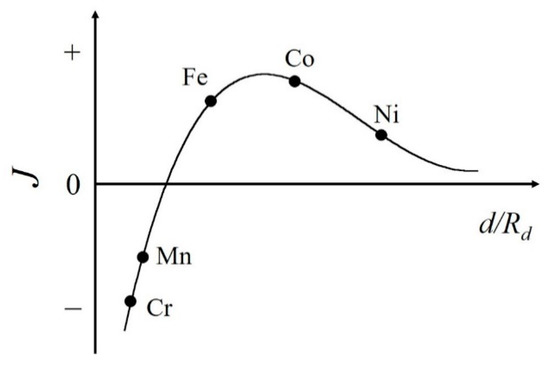
Figure 1. Schematic view of the Bethe–Slater curve. Here, J, d, and Rd represent the magnetic exchange coupling between atoms, the interatomic distance, and the radius of the 3d shell, respectively.
On the other hand, the effects of interstitial atoms in Mn-based compounds are not well researched. As shown in Figure 1, the Mn atom itself shows the AFM ground state, however the expanded Mn–Mn distance in Mn-based compounds leads to the FM state. Mn compounds are indispensable for both FM and AFM materials. For example, MnBi and MnAl have attracted much attention as permanent magnets [14][15][16][17][18]. MnSi has been extensively studied as a magnetic material with a skyrmion state, which is a noncollinear magnetic structure. The skyrmion domains can be driven by the low current density threshold [19]. Recently, Mn3Sn has been intensively studied as a topological antiferromagnet [20] and is a candidate next-generation spintronics material. If the effects of interstitial atoms are well understood, they can be highly useful in the development of spintronics devices or highly functional magnetic devices, which can be developed via easy on-demand control of the magnetic state.
We have surveyed Hydrogen-Absorbed (R or Th)6Mn23, Hydrogen-Absorbed YMn2, Carbon-Added Mn5Si3, (R or Actinide)Mn2Si2 and its germanides, Boron-Added Pd0.75Mn0.25 Alloy, and Boron-Added Sm2Mn8Al9. As in the rare-earth Fe-based compounds, the interstitial atoms give rise to the enhancement of FM interaction in the weak hybridization regime leading to the appearance of room temperature ferromagnetism. However, the Mn compounds surveyed above manifest the change or additional formation of magnetism by the interstitial atoms, while many rare-earth Fe-based parent compounds are already ferromagnets. The change from paramagnetic to FM state is observed in hydrogen-absorbed Th6Mn23, hydrogen-absorbed YMn2 or Sm2Mn8Al9Bx. The result of Mn5Si3Cx thin film may be a rare example of change from the AFM to FM state by the interstitial atoms. In Pd0.75Mn0.25Bx, the room temperature ferromagnetism is induced by a slight addition of boron, while the low-temperature magnetic ground state of the parent compound is unchanged. This can be regarded as an example of the additional formation of magnetism by interstitial atoms. It should be noted that, in some cases, the change or additional formation of a magnetic state seems to abruptly occur, which is valuable for future research. We note here that the magnetic structures have been divided into FM and AFM, although some compounds may show a more complicated state such as canted AFM, and spiral AFM. In the future, discussion taking into account a more microscopic mechanism of the magnetic ordering would be necessary.
The change in magnetism between FM and AFM states or the additional formation of new magnetic coupling at rather high temperatures by interstitial atoms is substantially valuable in a magnetic device integrated with both FM and AFM materials due to the easy on-demand control of magnetism in the fabrication process. At the present stage, Mn-based compounds fulfill the requirement of change or the additional formation of magnetism, while in Fe-based compounds, only improvements of FM properties are extensively investigated and the change (or the additional formation) of the magnetic state is not well explored. Focusing on the research area of the permanent magnet, a rare-earth Mn-based permanent magnet is still missing, although the MnBi-type magnets are well known. Based on the Bethe–Slater curve, Mn atoms favor the FM state with expanding Mn–Mn distance. Therefore, the density of Mn could not be so increased as in rare-earth Fe-based permanent magnets, resulting in a smaller saturation magnetization. However, there exists a large gap of BH energy product between the NdFeB magnets and ferrite magnets, and a rare-earth Mn-based permanent magnet may be a good candidate filling the gap [21].
Further improvement of magnetic properties in the on-demand control would be achieved by another strategy such as a composition effect and carrier doping. If a metallurgical phase diagram of a target compound possesses a homogeneity range, the magnetic ordering temperature often varies with the atomic composition. For example, the TC of Tb2Co2Ga ranges rather widely from 75 to 145 K by changing the starting composition [22]. Such a composition effect is reported in other compounds [23][24][25] such as Nd3Pd20Ge6, Tb3Co3Ga and Mn1+xGa. In many cases, the crystal structure parameters slightly change, which heavily affects the magnetic exchange interactions.
The magnetic anisotropy energy is one of the important factors in characterizing a ferromagnet. It is known that it can be tuned by doping, mainly due to the variation of the density of states near the Fermi level. The doping effect is reported in, for example, Ni2MnGa, SmCo5-xFe, MnBi, Nd2Fe17X (X = C or N), Ce2AuP3 and so on [26][27][28][29][30]. Taking into account the crystal symmetry, which is related to the magnetic anisotropy energy, a lower crystal symmetry with more tunable crystal parameters might be favorable.
Another interesting control of magnetism is the manipulation of spin by external fields such as the electric field and the optical light. For example, the employment of an electric double-layer transistor has achieved a control of magnetism by weak voltage [31]. Recently, an optical change in magnetism through the Kondo effect has been reported [32]. The interstitial atoms may precisely control the magnetism so that only a small magnitude of external field is required for the device working, and the power consumption can be highly reduced.
From the fundamental viewpoint, research into critical behavior is interesting. Actually, in strongly correlated electron systems, there have been plenty of studies for seeking a quantum critical point under the suppression of magnetism [33][34][35][36][37]. We speculate that a formation of FM exchange coupling above room temperature would be a discontinuous phenomenon as mentioned in the results of Mn-based compounds. While it is not well investigated for rare-earth Fe-based compounds, we note that RFe11TiCx and RFe11TiCx show a finite change in TC at an infinitely zero value of volume expansion depending on R species [38].