| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Isaac Bersuker | + 2460 word(s) | 2460 | 2020-12-09 17:07:20 | | | |
| 2 | Isaac Bersuker | Meta information modification | 2460 | 2020-12-11 17:18:44 | | | | |
| 3 | Isaac Bersuker | + 14 word(s) | 2474 | 2020-12-11 17:44:47 | | | | |
| 4 | Isaac Bersuker | + 16 word(s) | 2476 | 2020-12-11 23:14:52 | | |
Video Upload Options
The source of spontaneous symmetry breaking (SSB) in polyatomic systems, attributed to the Jahn-Teller effect (in electronic degenerate states) or to the pseudo-Jahn-Teller effect (under the condition of pseudodegeneracy), is complemented with the notions of hidden Jahn-Teller effect (h-JTE) and hidden pseudo-Jahn-Teller effect (h-PJTE) to stand for the cases when neither electronic degeneracy, nor pseudodegeneracy is present, but the system is still spontaneously distorted. The h-JTE and h-PJTE occur due to, respectively, the JTE and PJTE in the excited states of the undistorted system, but being strong enough, they penetrate its ground state forming a stable configuration with lower symmetry and (possibly) different spin.
1. Introduction
The source of spontaneous symmetry breaking (SSB) in polyatomic systems was first revealed by L. Landau in 1934 in a discussion with E. Teller, stating that the configuration of any nonlinear polyatomic system in a degenerate electronic state undergoes spontaneous distortions that remove the degeneracy [1], presently known as the Jahn-Teller effect (JTE) (see, e.g.,[2]). In an extension of this effect, it was shown that the spontaneous distortion may take place also when the degeneracy of the electronic state is slightly removed [3]. It served as a basis for a later on more important conclusion that the vibronic coupling between any two electronic states (often ground and excited) with any energy gap between them, under certain conditions of “pseudodegeneracy” may lead to structural instability and distortions. This is the pseudo-JTE (PJTE) [4][5].
An important generalization was reached by showing that the JTE and PJTE are the only sources of instability and distortions of high-symmetry configurations of polyatomic systems [2][4][5], meaning that the variety of properties of molecular systems and solids related to their SSB can be explained by involving these effects. This important conclusion has been challenged by examples of molecular systems, which at face seem to contradict to its statement. Indeed, there are molecules with SSB of their high-symmetry configurations, in spite of being in nondegenerate states (no JTE), with no appropriate excited state to induce the PJTE (e.g., when the excited states of appropriate symmetry are too high in energy or have a different spin multiplicity, see below). It was shown [6] that in such cases the distortions are still due to the JTE or PJTE, which originate in the excited states, but, being sufficiently strong, they penetrate the ground state, producing additional lower (global) minima of the adiabatic potential energy surface (APES), in which the system is distorted. They are called “hidden” JTE and “hidden” PJTE (h-JTE and h-PJTE, respectively) because they are not seen directly as a feature of degeneracy and pseudodegeneracy in the reference high-symmetry configuration; they appear only when the special role of an excited state in their formation is recovered.
2. Hidden Jahn–Teller and Pseudo-Jahn–Teller Effects
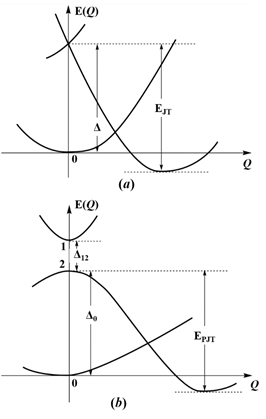
Figure 1 illustrates this statement. We see that the ground state of the system is stable in the high-symmetry configuration at Q=0, but it is unstable in this configuration in the lowest excited double-degenerate state due to the JTE (Fig. 1a), or due to the pseudodegenerate interaction with a higher state in the PJTE (Fig. 1b). If these excited-state effects are sufficiently strong, their stabilization energies may offset the energy gap to the ground state (EJT>Δ in the h-JTE or EPJT>Δ in the h-PJTE case) and produce additional global minima, in which the equilibrium ground state is distorted [6]. In the case of the h-JTE triggered by the E⊗e JTE problem in the excited state, the additional configuration occurs when (F2/2K0)>Δ, where F is the vibronic coupling constant, and K0 is the primary force constant, while for the h-PJTE the condition of a possible additional stable configuration is more complicated [6]:
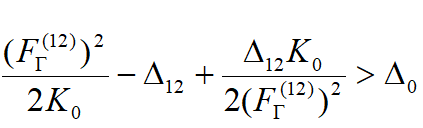
where F(12) is the constant of vibronic coupling between the two excited states, and the constants Δ12 and Δ0 are shown in Fig.1b. In both cases, h-JTE and h-PJTE, under the above conditions, we get two stable configurations, distorted and undistorted, but distinguished from the JT case, where the possible distortions are restricted by the JT active modes, the PJT induced distortion may be of any kind, dependent on the symmetries of the mixing excited states. Another distinguished feature of the h-PJTE is that it leads to orbital disproportionation [7].
Figure 1. Illustration of the origin of h-JTE and h-PJTE. In both cases the distortion of the system in the ground state global minimum of the APES is due to the JTE (a), or PJTE (b) in the excited state; it takes place when their stabilization energy (respectively, EJT or EPJT) is larger than the energy gap to the ground state of the high-symmetry configuration (Δ and Δ0, respectively); Δ12 is the energy gap between the two excited states producing the h-PJTE.
Actually, systems with h-JTE and h-PJTE are very widespread and influence a variety of observable properties, but they were not recognized as such before the theoretical exploration [6]. As clearly seen from Fig. 1, one of the important consequences of the h-JTE and h-PJTE is that they result in bistabilities, meaning they produce two equilibrium configurations of the system with different geometry, distorted and undistorted, and possible different magnetic properties when the two electronic states of the reference high-symmetry configuration have different spin-multiplicity [8]. Obviously, the properties of the specific systems with such bistabilities depend on their parameter values. They were estimated by ab initio calculations for a series of molecular systems and local formations in solids [8]. Below we show illustrative examples.
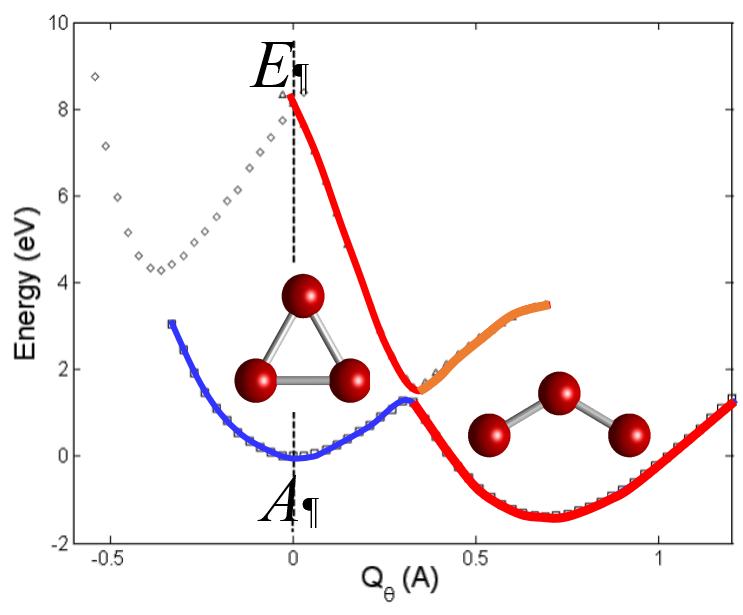
The h-JTE was first demonstrated on the structure and properties of the ozone molecule O3 [7] for which ab initio calculations [9][10] show that in the high-symmetry regular-triangular geometry the ground state 1A is nondegenerate, and its excited double degenerate 1E state is rather high, at the energy gap Δ~8.5 eV, so no JTE or PJTE is expected in the reference high-symmetry configuration. Nevertheless, the regular-triangular configuration of O3 is not the ground-state one: its APES has lower-in-energy three equivalent minima, in which the configuration of the molecule is obtuse-triangular (with a nonzero dipole moment). The ab initio calculation of the cross-section of the APES of this molecule along the distortion coordinate Q, carried out including the ground 1A state and first excited 1E state [11] follows the prediction of the theory for the h-JTE: the three equivalent obtuse-triangular configurations with lower energy emerge from the E⊗e problem of the JTE in the excited 1E state, yielding a strong stabilization energy EJT~9eV that penetrates the energy gap of ~8.5 eV (Fig. 2).
Figure 2. (Color online) Cross-section of the APES of the ozone molecule along the Qθ component of the double degenerate e mode, obtained by numerical ab initio calculations including the highly excited E state, explicitly demonstrating that the ground state distorted configurations are due to the JTE in the excited state. The global minimum is at Qθ= 0.69Å and the E-A avoided crossing takes place at Qθ~0.35Å (Reprinted with permission from Ref. 11. Copyright 2006 American Physical Society).
Note, that in the case of the ozone molecule both the ground state and the excited state, responsible for the h-JTE, have the same spin state. Therefore the two stable configurations, distorted and undistorted, have the same magnetic properties, hence the bistability in this case created by the h-JTE is simply dielectric: dipolar-nonpolar. However, if the two electronic states, participating in the hidden effects possess different spin states, the bistability would be both polar and magnetic. Below we demonstrate this by the examples from h-PJTE that incorporate a whole class of molecular systems and solids. There are also cases when both the h-JTE and h-PJTE take place simultaneously in the same system (see, e.g., the electronic structure of the CO3 molecule [12]).
3. Half-Filled Closed-Shell Degenerate Electronic Configurations with h-PJTE and Spin Crossover
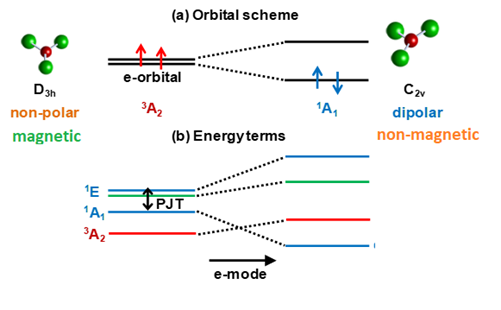
With respect to the h-PJTE induced bistabilities, the cases of half-filled closed-shell electronic e2 and t3 configurations that occur in a wide range of molecular and solid-state systems are very illustrative. The JTE nature of possible distortions of the ground state of such systems is “hidden” because their closed-shell charge distribution is totally symmetric. The energy terms formed by the interelectron interactions in e2 configurations is shown in Fig. 3. We see that in these cases the ground state of the undistorted configuration (triangular, octahedral, etc.) is a spin triplet, 3A2 , but a strong PJTE mixing of two excited singlet states, 1A1 and 1E, may produce an additional lower-energy state with a distorted configuration (provided the stabilization energy EPJT is larger than the energy gap Δ to the ground state, as in Fig. 1b)). For a triangular system, the distorted configuration has a non-zero dipole moment, but a zero magnetic moment (zero spin from the 1A1 state), whereas the undistorted configuration in the 3A2 state has a zero dipole moment, but a nonzero magnetic moment.
The two different spin states of the two energy-minima configurations is a remarkable feature of systems with half-filled closed-shell e2 and t3 configurations. It is directly related to orbital disproportionation [7], when the triplet 3A state (formed by the two electrons that occupy the two e orbitals with parallel spins), which is expected to be the ground state according to the Hund’s rule, is overridden by the 1A state with zero spin (with two electrons with antiparallel spins in one e orbital), the whole process being driven by the PJTE that lowers the energy.
Figure 3. |Illustration to the formation of two coexisting configurations with different magnetic and structural properties: (a) In a typical orbital energy level scheme of the electronic e2 configuration the ground state 3A2 is formed by the two electrons with parallel spins, each of them occupying one e orbital, resulting in the eθ↑eε↑ configuration, which is totally symmetric and magnetic (the spin S=1); the picture shows the example of a planar triangular molecule (e.g.,CuF3); (b) In the energy terms scheme of the same electronic e2 configuration the first excited singlet state 1A1 with the electron configuration (1/√2)(eθ↑eθ↓ + eε↑eε↓) is totally symmetric too, but due to the PJT interaction with the higher 1E1 state it undergoes the orbital disproportionation resulting in either eθ↑eθ↓ or eε↑eε↓ configurations, both having a lower symmetry of charge distribution that distorts the systems in the e mode direction, but a zero spin state.
A quite similar effect takes place in the case of electron configuration t3. In this case, the interelectron interaction spans the states 4A2, 2T1 , 2E and 2T2 , with the ground quadruplet state 4A2, which corresponds to the Hund’s rule distribution Ιtx↑; ty↑; tz↑>. A strong PJTE coupling between the two excited states 2T1 and 2T2 results in a lower orbital disproportionate component of the type Ιtx↑; ty↓; tz↑> with a doublet spin-state instead of the quadruplet in the high-symmetry configuration [7].
As follows from these results, orbital disproportionation in systems with half-filled closed-shell electronic configurations is necessarily accompanied by lowering the spin of the electronic ground state. For the e2 configuration it means transition from the high-spin (HS) triplet 3A state to the low-spin (LS) singlet state 1A, while for t3 this transition is from the quadruplet (HS = 3/2) to the doublet (LS = ½) state. Since this transition is induced by the PJTE distortion originating from an excited electronic state, the two states, HS undistorted and LS distorted, coexist in two minima of the APES which may have close energies (Fig. 2). In between these two minima there is a crossing between the two states of different spin, a spin crossover. The results of ab initio calculations [7][8][11] show explicitly the spin crossover that takes place in the specific molecules and solids under consideration. It is demonstrated above to take place in molecular systems with electronic e2 and t3 configurations, meaning molecules with at least one three-fold axis of symmetry and the appropriate number of electrons, as well as in solids with corresponding bands, but it may be expected in any systems with h-JTE or h-PJTE.
In the e2 and t3 systems the spin of the two nuclear configurations, distorted and undistorted, is different, with a higher spin in the undistorted configuration. This leads directly to magnetic moment μ bistability (μ1;μ2). For e2 systems, the magnetic moment of the undistorted HS configuration with the spin S=1 is μ1 ~ 2.82 MB, while for the distorted LS geometry S=0 and μ =0, realizing a (2.82 MB; 0) magnetic bistability. On the other hand, the two geometries have different dielectric properties, e.g., dipole moments p, leading to dipolar bistability (p1; p2). Often the distorted LS configuration has a non-zero dipole moment, whereas p=0 in the undistorted HS one, resulting in (0; p) bistability. Thus in such systems we have two coexisting bistabilities, magnetic (2.82 MB; 0) and dipolar (0; p), with interesting (and peculiar) properties of either magnetic moment, but no dipole moment in one of the coexisting states, or dipole moment, but no magnetic moment in the other state. Following the often-used terminology, such systems can be termed single-molecule multiferroics.
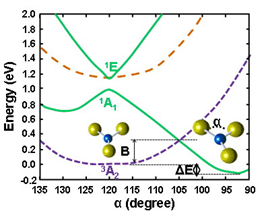
As demonstrative examples, we show here the results of ab initio calculations of the h-PJTE in the molecule CuF3 with symmetries D3h where the Cu3+ ion has the valence electronic d8 configuration, the outer two d electrons of which occupy the e orbitals forming the e2 configuration [11]. The latter produce the noted above three terms (Fig. 3), which in the D3h symmetry of CuF3 are labeled as 3A2' (ground state), 1A1', and 1E'. The results of full scale (high-level) ab initio calculations of all these terms in CuF3 as a function of the e type distortions (labeled by the angle α(F-Cu-F)) are shown in Fig. 4. We see that, in accordance with the general theory, there is a strong PJTE interaction between the two excited 1A1', and 1E' states, due to which the lower 1A1' state goes sharply down, crosses the triplet ground state of the undistorted configuration and produces a global minimum with a distorted (α~930) LS geometry. The difference between the zero-point energies of these two configurations is 0.190 eV (all energies read-off the zero-point vibrational levels), while their excitation energies to the point of spin-crossover (barrier heights) are δHS=0.541 eV and δLS=0.712 eV, respectively. In the distorted configuration the magnetic moment m=0 and the dipole moment p= 1.67 D, and in the undistorted state, as mentioned above, μ=2.82 MB with p=0. Thus we get a perfect case of bistability, (2.82MB; 0) vs. (0; 1.67D), in which the two stable configurations are separated by both potential and magnetic (spin) barriers. Other examples including local formations in solid states see in [12][13].
Fig. 4. Ab initio calculated energy profiles of the planar CuF3 molecule in the ground and lowest excited states as a function of the angle α (e mode distortion of the D3h configuration), showing the formation of two equilibrium geometries with the lower energy one distorted at α~930, induced by the h-PJTE via two excited states [8]. The distorted and undistorted configurations have different spin multiplicity (magnetic moments) and different dipole moments. Reproduced with permission from ref. 8. Copyright (2011) American Physical Society.
References
- Teller, E. A Historical Note. In Englman, R. The Jahn-Teller Effect in Molecules and Crystals; Wiley: London, 1972, Foreword.
- Bersuker, I.B. The Jahn-Teller Effect; Cambridge University Press: Cambridge, UK, 2006.
- Öpik, U.; Pryce, M. H. L. Studies of the Jahn-Teller effect I. A survey of the static problem. Proc. R. Soc. London 1957, A 238, 425-447.
- Bersuker, I.B.; Polinger, V.Z. Vibronic Interactions in Molecules and Crystals; Springer-Verlag: Berlin/Heidelberg, Germany, 1989.
- Bersuker, I.B. The Pseudo Jahn-Teller Effect—A Two-State Paradigm in Formation, Deformation, and Transformation of Molecular Systems and Solids. Chem. Rev. 2013, 113, 1351–1390.
- Bersuker, I.B. Recent Developments in the Jahn-Teller Effect theory. The Hidden Jahn-Teller Effect. In The Jahn-Teller Effect. Fundamentals and Implications for Physics and Chemistry; Köppel, H., Yarkony, D.R., Barentzen, H., Eds.; Springer Series of Chemical Physics; Springer: Heidelberg, Germany, 2009; Volume 97, Chapter 1, pp. 3–23.
- Garcia-Fernandez, P.; Bersuker, I.B.; Boggs, J.E. Orbital disproportionation and spin crossover as a pseudo-Jahn-Teller effect. J. Chem. Phys. 2006, 125, 104102.
- Garcia-Fernandez, P.; Bersuker, I.B. A class of molecular and solid-state systems with correlated magnetic and dielectric bistabilities induced by the pseudo-Jahn-Teller effect. Phys. Rev. Lett. 2011, 106, 246406.
- Siebert, R.; Fleurat-Lessard, P.; Schinke, R.; Bittererová, M.; Farantos, S.C. The vibrational energies of ozone up to the dissociation threshold: Dynamics calculations on an accurate potential energy surface. J. Chem. Phys. 2002, 116, 9749.
- Babikov, D.; Kendrick, B.K.; Walker, R.B.; Pack, R.T.; Fleurat-Lessard, P.R.; Schinke, R. Metastable states of ozone calculated on an accurate potential energy surface. J. Chem. Phys. 2003, 118, 6298.
- Garcia-Fernandez, P.; Bersuker, I.B.; Boggs, J.E. Lost topological (Berry) phase factor in electronic structure calculations. Example: The ozone molecule. Phys. Rev. Lett. 2006, 96, 163005.
- Liu, Y.; Bersuker, I.B.; Zou, W.; Boggs, J.E. Combined Jahn-Teller and pseudo Jahn-Teller effects in the CO3 molecule: A seven-state six-mode problem. J. Chem. Theory Comp. 2009, 5, 2679–2686.
- Bersuker, I. B., Spin crossover and magnetic-dielectric bistability induced by the hidden pseudo-Jahn-Teller effect, Magnetochemistry, 2020, 6, 64; doi:10.3390/magnetochemistry6040064.