1000/1000
Hot
Most Recent

The program was developed by the IEMES (Structural Integrity: Materials and Structures) Research Group at the University of Oviedo, in collaboration with Prof. Castillo of the University of Cantabria and Empa-Dübendorf (Swiss Federal Laboratories for Materials Science and Technology). ProFatigue is based on the Weibull’s regression model proposed by Castillo-Canteli in order to satisfy the physical and statistical conditions required by any valid fatigue model.
It has been validated through its successful application to a wide range of materials and practical cases since its launch in 2014, including the fatigue assessment of bio-mechanical materials. Its application in fatigue testing research in the field of dentistry would constitute a significantly improved alternative to those currently proposed in the ISO 14,801 standard (the simplified S-N curve definition and the staircase method), not only because of its accuracy in the fatigue limit estimation itself, but also its ability to provide the probabilistic definition of the whole S-N field of the studied implant or prosthetic component, which would result in much more precise predictions of the lifetime of these components.
The ProFatigue software represents a statistical tool that facilitates the probabilistic definition both of the S-N field (stress-number of cycles) and ε- N field (strain-number of cycles), according to the testing reference parameter. Consequently, it allows for the graphical representation of the predicted number of cycles needed to reach failure in a particular fatigue test from some experimental results, previously obtained and deduced from the applied load or deformation. To do so, the software estimates the five regression model parameters, three of which define the Weibull’s subjacent three-parameter distribution function.
The main advantages of this model include:
1. The possibility of an optimized test planning campaign, which results in a reduction in the total number of tests required and its rationalization, by avoiding the undesirable outcome of run-outs, or at least reducing them to an acceptable number. Thus, the S-N field is determined by a number of tests not previously stated, and in any case, far fewer than those currently required by the ISO standard for the same level of confidence. Furthermore, given the normalization property that sustains the model, it is unnecessary to repeat the tests under the same load range, with any negative consequences for the completion of the statistical analysis (see Part 2). This contrasts with the alternative procedures to determine the S-N field presented by the current ISO standard, which require numerous tests for the same load range.
2. The complete S-N field is reduced to a simple distribution function of the normalized variable, V, which is deduced as the combined expression of both stress range and number of cycles, through the expression V = log(N/N0) log(Δσ/Δσ0), where N0 is the number of limit cycles and Δσ0 is the endurance limit for a theoretically infinite fatigue limit. This normalization allows the optimized planning of the testing campaign, in addition to the combined evaluation of different levels of test results as belonging to a single homogeneous group. This increases the reliability of the deduced model, and ultimately, it allows for the detection of possible bias in the joint distribution, thanks to the non-randomness of the results obtained from the different tested load levels, which would point out an anomalous behavior, that may be worthy of further study.
3. The possibility of a simple calculation of the number of cycles for a given particular stress range and probability, or conversely, of the stress range for a predetermined number of cycles and probability, is a direct consequence of the S-N field analytic expression. This paragraph is directly related to paragraph 1, regarding its application as a means of support for fatigue program planning.
It is important to note that the fatigue programs related to the S-N field evaluation, including ProFatigue and other current programs, are focused on predicting the probability of reaching the terminal state of the implant, not necessarily failure. On the contrary, crack growth evolution, as a cumulative damage process inherent to the fatigue phenomenon, requires performing tests using sophisticated experimental techniques (such as potential drop, acoustic emission) to measure the physical crack growth evolution. In this case, a damage tolerance concept would be convenient in order to aid in the decision to either remove the implant or perform a restorative intervention. This is an interesting question to be considered for future implant research.
The program enables the visualization of the S-N field as the project progresses with the incorporation of new data (see Figure 1). In this way, a rational definition based on a probabilistic approach of the stress to be applied in the next test is established, and therefore the S-N field is defined according to an optimized strategy. This makes it possible to rationally save tested specimens and simultaneously achieve greater reliability in the parameter determination of the model.
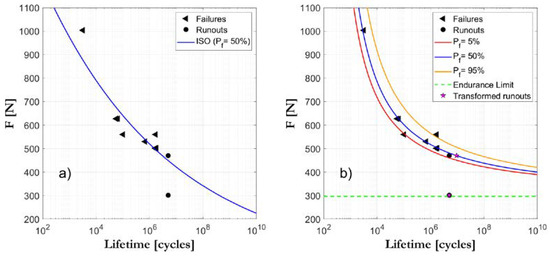
Figure 1. Comparative example between the ISO standard S-N field definition (a) and the ProFatigue S-N field definition (b) for the same studied case.
Three run-out tests, carried out at different load ranges, could potentially be enough to secure an initial approach to the S-N field, although it would not guarantee a representative estimation of the scatter. Therefore, in order to obtain a reliable definition of the S-N field, 8–10 specimens would be sufficient in most cases, as long as there is an appropriate distribution of the load ranges (see Figure 2). A second level of analysis of the confident intervals would require applying either a “boot-strap” statistical method or the use of Bayesian techniques.
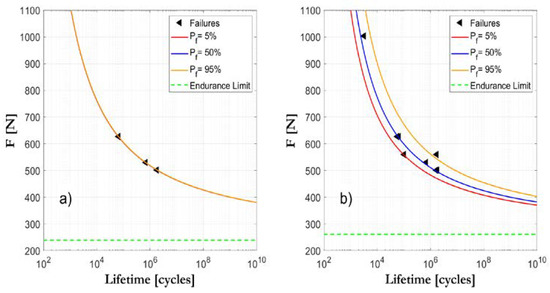
Figure 2. Example of assessment of the S-N curves by applying the ProFatigue program to the experimental data: provisional initial evaluation after the first three tested specimens (a); final evaluation, after eight tested specimens (b).
As is evidenced above, the ProFatigue software provides more comprehensive information and requires far fewer tests than the other methods outlined in this paper. The program offers an analytical definition of the S-N probabilistic field through percentiles associated with the desired probability and, in doing so, allows for the prediction of the lifetimes over the testing limits by extrapolation. This means that the fatigue limit for any probability can be calculated, not only for the 5 × 106 or 2 × 106 cycles predetermined by the ISO standard, but also for an infinite number of cycles (endurance limit or real fatigue limit), or any other desired number of cycles. Obviously, even the longest lasting implants will not exceed 80 × 108 cycles (around 80 years in case they are placed in a young person), and therefore the calculation of the fatigue limit for an infinite number of cycles may not be of interest from a clinical point of view. However, in terms of in vitro tests, the ProFatigue software allows a much stricter and far more precise comparative analysis of specimens and a far more accurate real fatigue limit definition for each studied model.
The ProFatigue software is available free of cost through the link https://meteo.unican.es/temp/castie/Profatigue. A user guide is also available, providing a detailed step-by-step overview of the program and installation.
Once downloaded, the program can be run in either manual or guided mode; however, only the guided mode enables the user to introduce the fatigue testing results step by step. Upon entering the experimental outcomes (number of cycles until failure, request range and identification of the specimens designated as survivors or run-outs, if any), the program supplies the estimated values of the five model parameters and displays the S-N field with the percentile curves corresponding to the chosen failure probability. By default, probabilities of 0, 1, 5, 50, 95 and 99% are shown. In addition, the implemented model in ProFatigue allows for the possibility of virtually transferring the run-outs to the position where the failure could be probabilistically expected. The program also permits a number of options in the estimation process, such as excluding any data of doubtful reliability or survivors tested below the fatigue limit. It is also possible to consider the scale effect, when appropriate to apply.
While the program itself is extremely straightforward, expert engineer support (particularly during the design of the testing strategy and the final global evaluation) is advisable in order to ensure a correct understanding of the criteria that rule the successive decision-making process in the test campaign. This support facilitates a real-time evaluation of the S-N field from the available results, with the objective of maintaining an optimized approach.
The ProFatigue program allows a probabilistically advanced estimation of the remaining lifetime of the implant but does not provide an estimation of the crack size evolution. The same would happen with any other current S-N evaluation software. To provide the progress of the crack size, fatigue tests must be performed on the implant material and crack growth must be registered by using sophisticate experimental techniques, such as potential drop, acoustic emission. With this information, a damage tolerance concept could be applied to decide on possible withdrawal of the implant or the restorative intervention. This is an objective to be envisaged for a new investigation on implants.
[1] Castillo E., Fernández-Canteli A. A unified statistical methodology for modeling fatigue damage Springer, 2009
[2] Castillo E., Fernández-Canteli A., Pinto H., López Aenlle M. A general regression model for statistical analysis of strain-life fatigue data Materials Letters, 62, 3639-3642, 2008.
[3] Castillo E., Ramos A., Koller R., López Aenlle M., Fernández-Canteli A. A critical comparison of two models for assessment of fatigue data Int. Journal of Fatigue, 30, 45-57, 2008.
[4] Pascual F.J., Przybilla C., Gracia-Villa L., Puértolas J.A., Fernández-Canteli A. Probabilistic assessment of fatigue initiation data on highly crosslinked ultra high molecular weight polyethylenes Journal of the Mechanical Behavior of Biomedical Materials, 15,190-198, 2012
[5] Pyttel B., Fernández-Canteli A., Argente-Ripoll A. Comparison of different statistical models for description of fatigue including very high cycle fatigue Int. Journal of Fatigue, 93, 435-442, 2016.
[6] Muñiz-Calvente M., Fernández-Canteli A., Pyttel B., Castillo E. Probabilistic assessment of VHCF data as pertaining to concurrent populations using a Weibull regression model Fatigue and Fracture of Eng. Materials and Structures, 40, 1772-1782, 2017.
[7] Fernández-Canteli A., Przybilla C., Nogal M., López-Aenlle M., Castillo E. ProFatigue: A software program for probabilistic assessment of experimental fatigue data sets Procedia Engineering, 74, 236-241,2014.