Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1 Optical feedback interferometry makes imaging possible at whatever wavelength a semiconductor laser exists and allow multi-parametric mapping of the target
Maurizio Dabbicco
 + 2642 word(s) 2642 2020-11-17 08:21:23 |
2 format correction
Peter Tang
 -14 word(s) 2628 2020-11-18 10:18:55 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Brambilla, M.; Columbo, L.L.; Dabbicco, M.; De Lucia, F.; Mezzapesa, F.P.; Scamarcio, G. Scanless and Detectorless Imaging System. Encyclopedia. Available online: https://encyclopedia.pub/entry/3085 (accessed on 19 April 2024).
Brambilla M, Columbo LL, Dabbicco M, De Lucia F, Mezzapesa FP, Scamarcio G. Scanless and Detectorless Imaging System. Encyclopedia. Available at: https://encyclopedia.pub/entry/3085. Accessed April 19, 2024.
Brambilla, Massimo, Lorenzo Luigi Columbo, Maurizio Dabbicco, Francesco De Lucia, Francesco Paolo Mezzapesa, Gaetano Scamarcio. "Scanless and Detectorless Imaging System" Encyclopedia, https://encyclopedia.pub/entry/3085 (accessed April 19, 2024).
Brambilla, M., Columbo, L.L., Dabbicco, M., De Lucia, F., Mezzapesa, F.P., & Scamarcio, G. (2020, November 18). Scanless and Detectorless Imaging System. In Encyclopedia. https://encyclopedia.pub/entry/3085
Brambilla, Massimo, et al. "Scanless and Detectorless Imaging System." Encyclopedia. Web. 18 November, 2020.
Scanless and Detectorless Imaging System
Edit
This entry is adapted from the peer-reviewed paper 10.3390/s20205930

Optical feedback interferometry is a versatile and robust technology for both sensing and imaging applications, available at all wavelengths were a semiconductor laser exists, from 270 nm to 120 μm. It can be easily adapted to fiber integrated systems and promises to be compatible also to silicon photonics.

coherent imaging semiconductor lasers laser self-mixing multimodality single-pixel compressed sensing terahertz imaging multispectral imaging

1. Introduction 

A number of excellent reviews [1][2][3][4][5], two books [6][7], and a few book chapters [8][9][10], among the others, have been published on the subject of laser self-mixing, as it was initially named, or optical feedback (OF) interferometry, as it is more often termed today.

OF happens when part of the radiation emitted by a laser source is coupled back to the laser cavity before losing coherence. It happens, or may happen, in all experiments with a laser source if no specific care is taken in order to avoid it. OF always pushes the laser emission to change its instantaneous values of frequency and power. Whether it is a trouble or a benefit, mostly depends on the way we look at. It is a trouble for the stability of laser emission if the OF is uncontrolled; it can be a benefit when OF is under the researcher's control and intended for some purpose; for example, linewidth narrowing [11], chaos synchronization [12] or sensing applications [13]. The changes induced by OF on the instantaneous laser frequency and power bring information on the optical properties of the whole system, the laser itself, the target responsible of the back scattering (or back reflection), and the optical path length in between. The whole system is a nonlinear optoelectronic system, possibly experiencing regimes of dynamical instability interspaced with regimes of stationary behavior. Most of the practical sensing schemes based on OF analyze the information conveyed by the variations of the stationary parameters caused by modifications of the radiative field amplitude and phase occurred along the optical path forth and back from the target.

Information density conveyed by the field spatial frequency (k) increases in going from a collimated to a focused beam and can be tailored by structuring the optical field by means of, for example, spatial light modulators. Spatial frequency relates to image resolution and OF imaging has demonstrated the potential to beating the diffraction limit [14][15]. On the other hand, the natural reference unit of interferometric measurement is the fringe, so that fringe-counting is the simplest possible signal analysis. However, it is limited to quantized results multiple of the laser half-wavelength λ/2 or the inverse of the laser linewidth Δν (Δϕ = 2π = 2π/λ2Δx = 2πΔνt −> Δx = λ/2 or t = 1/Δν). Better sensitivity can be achieved by phase retrieval algorithms [16] or phase-locking techniques [17], and OF is challenged by reaching 10−4λ resolution [18].

The Rubik-like cube illustrated in Figure 1 symbolizes our idea of the OF expansion capability. The versatility of OF systems is represented on the third axis: from the simplest single-channel to multiple parallel channels, OF has matured the chance of going multi-modal [19][20][21]. Axes 1 and 2 measure the information increase due to improving time and space resolution.

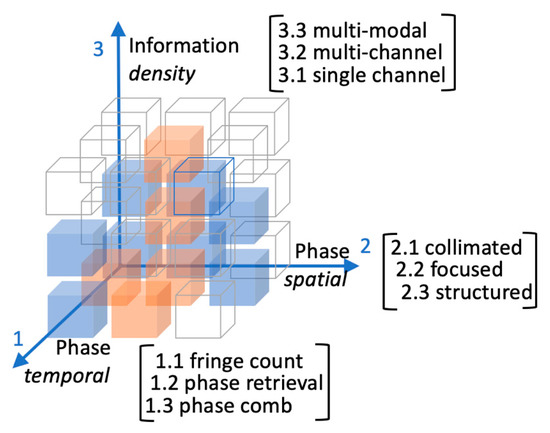
Sensors 20 05930 g001 550

Figure 1. A suggestive drawing of the optical feedback (OF) development space. Axes 1 and 2 measure the information increase due to improving temporal and spatial resolution. Along axis 3 the information content achievable with more sophisticated OF setups. Blue cubes make the content of this article. Orange cubes are regions explored by other groups cited in the text.

2. Basic Principles and Modeling Equations

The laser near threshold is a highly nonlinear system quite sensitive to any perturbation of the energy density equilibrium inside the cavity between carriers and the electromagnetic field. Any radiation coherent with the intracavity field entering the laser would disturb the dynamic equilibrium forcing the system to find a different working point. What is actually measured in OF experiments is the attempt of carriers and photons to restore the energy density balance given the feedback physical dimensions: amplitude, phase, and frequency.

The most famous rate equation model including the effect of OF in a semiconductor diode laser (SDL) was proposed by Lang and Kobayashi in 1980 [22] and, despite its limitations, is still widely used today, also for other types of lasers. With respect to the free running laser system, the model is characterized by the feedback delay τ and the feedback strength κ. A systematic experimental verification of the Lang–Kobayashi model was made a few years later by Tkach and Chraplyvy [23] who identified five dynamical regimes in the τ−κ space.

In 1984, Acket et al. [24] introduced another parameter to characterize the OF strength C = κτε(1+α2)1/2, since then renowned as the feedback parameter C, the most immediate, and quantitative, identifier of the OF dynamical regimes. C enters into play in the definition of the stationary laser emission mode frequency, with (ωF) and without (ωS) OF:

Once recognized that ωτ = ϕ, this equation holds the name of excess-phase equation (EPE) and is interpreted as the phase response of the system ϕF to the phase stimulus ϕS (the phase accumulated by the emitted field in a complete round trip forth and back to the target when C = 0). EPE is the workhorse equation for OF simulations in a large variety of experiments where the change of ϕS(t) is slow on the time scale of carriers and photons relaxation and the optical field can be considered single mode. The importance of EPE cannot be overestimated since its shape defines the envelope of the OF signal in almost all practical cases. In fact, both the modulation of the laser power and of the laser terminals voltage drop are demonstrated to be proportional to cos(ϕF).

It is quite obvious from its own definition, that the value of C is affected by the linewidth enhancement factor (LEF) α, or Henry factor [25], a phenomenological parameter coupling the refractive index dependence to the gain dependence on the carrier density in semiconductor lasers. Since α ~ 0 in quantum-cascade lasers (QCLs) and α >> 0 in SDLs, the latter will have a larger C-value, the other parameters being equal, thus making SDLs typically more unstable against OF than the QCLs. The longer the temporal delay τ of the feedback field, the larger its effect on the phase shift is. τ is usually expressed in terms of the optical distance laser-target τ = 2Ln⁄c, thus designating two immediate "measurement channels": refractive index and external cavity length.

It may be less obvious, but the target surface affects the value of C in two different ways: by its complex reflectivity, included in the definition of κ; and by the so-called mode-matching factor ε, the ratio of feedback power actually coupled back into the laser cavity because of geometrical constrains. Target related geometrical constrains, such as surface scattering and surface anisotropy should be considered as well as cavity related geometrical factors, like spatial light modulators, beam divergence or optical apertures. 

For the purpose of OF imaging, we distinguish only three operative regimes [3]: (i) weak feedback (C < 1) where the amplitude of the OF fringes is proportional to the feedback power; (ii) moderate feedback (1 < C < 4.6) where the OF fringes become sawtooth-like and the system is only bi-stable; (iii) strong feedback (C >> 10) where the system is largely multi-stable, the fringes flatten, and the OF signal loses phase information. Outside of these regimes, the OF signal exhibits irregular and even chaotic fluctuations suitable to extract statistical information on the system dynamics, but unmanageable for sensing applications.

3. Single Mode Feedback Imaging

The amplitude of the OF signal retains its dependence on the target optical properties and scanning the laser spot across the sample surface enables imaging of the target refractive index distribution, of the extinction coefficient distribution, and ultimately of the target complex reflectivity.

Refractive index is by far the most relevant contrast mechanism in reflective coherent imaging modalities. Minute changes of the local refractive index modulate the phase front of the reflected beam enabling the tracing of the edges of the sample morphology. OF imaging often allows for two different regimes: a weak feedback regime where the fringe amplitude is determined by the optical phase and a strong feedback regime where the signal amplitude is determined by the optical power. An exemplary image recorded in those regimes is reported in Figure 2, where the central part of the word SONY printed onto a CD is recorded by a QCL at 6.2 μm. In case of a non-uniformly flat sample, additional OF fringes occur because of the effective ΔL ≠ 0 while scanning the surface. This additional information may actually be evaluated to add depth resolution to the OF images [26].

Figure 2. Left panel: fringe amplitude dependence on feedback level, expressed in term of the κ-parameter. Right panel: at low feedback level (upper half) OF fringes are clearly distinguishable superposed to the index contrast image, due to surface misalignment from the optic axis. At large feedback level (lower half) the OF signal loses phase information of the reflected beam and is defined by the feedback power only (adapted from Reference [27]).

The optical power contrast capability permitted in the strong feedback regime appears to be potentially valuable to expand the OF imaging by including the mapping of chemical elements dispersed in the sample. The longer wavelengths made available by QCLs offer the opportunity to extend OF sensing to materials analysis and chemical imaging, since most of the molecular distinctive absorption features occur in the mid infrared spectral range. One of the most relevant absorption band in biological materials, often addressed as a target to distinguish healthy from diseased tissues, is the amide-I band around 1550–1580 cm−1 (6.3–6.5 μm). Common potato starch also shows a broad absorption feature in the same range, due to carbon–oxygen bonds, and was used as a phantom to calibrate OF sensitivity to absorption change. Figure 3 shows the OF image of two pills, one of potato starch (absorbing at 6.2 μm) and one of Intralipid® (transparent at 6.2 μm) in agar–agar matrix, prepared and included into a dehydrated agar–agar matrix (transparent at 6.2 μm); OF signal of a MIR-QCL at 6.2 μm only detected the potato starch pill. 

Figure 3. Top: transmittance infrared spectra of agarose (black), Intralipid® (grey) and potato starch (blue). Bottom: images of potato starch (upper) and Intralipid® (lower) pills in agarose matrix. Left panel shows the OF image taken at 6.2 μm by raster scanning the MIR-QCL beam. Right panel shows a photo of the sample (adapted from [28]).

The samples were prepared to be inhomogeneous and diffusive in order to mimic the scattering properties of real tissues. Back scattered light from this type of samples propagates with large speckle fluctuations lowering the image contrast and limiting the actual resolution.

4. Multimode Feedback Imaging

There are very few examples in literature of OF in multi-mode lasers [29][30][31]. With the goal of scanless and detectorless multimodal imaging, we show opportunities foreseen in multi-transverse mode lasers (stepping one step further along axis 3 in Figure 1. Vertical Cavity Surface Emitting Lasers (VCSELs) are intrinsically multi-transverse mode, even relatively small area VCSELs show polarization dynamics, often accompanied by spatial mode switching. In the simplest case of only two spatial modes spatially shaped feedback can be tailored to simultaneously detect two orthogonal degrees of freedom of motion with a single OF module [32][33]: longitudinal displacement (on-axis) and transverse rotation (roll), as seen in Figure 4.

A larger number of transverse modes can be accommodated in broad area VCSELs, whose complex dynamics can be regulated by incorporating a phase coupling mechanism inside of the cavity structure or by providing a suitable external feedback. Frequency detuned feedback, like that at work in OF Doppler velocimetry, is one way to change the laser mode configuration, as demonstrated in Reference [34]. Photonic-crystal VCSELs, as they are called, might then work as phase-sensitive CCDs taking scanless OF phase-contrast images as conventional CCDs take single-shot intensity-contrast images. Initially available only at near-infrared wavelengths, phase-coupled QCL arrays were recently realized also in the THz spectral range [35].

Figure 4. (a) Left: Temporal evolution of the modal intensities of the TEM10 and TEM01 modes of free-runningVCSEL. The blue trace represents the sum of the modal intensities. (b) Time plot of the modal intensities during a feedback mask rotation from Θ = 0 (left inset mask) to Θ = π (right inset mask). The insets show image plots of the numerical simulation of the field intensity variation (adapted from Ref. [32]).

A plain demonstration of multimodality allowed by OF imaging is shown in Figure 5. Three different visible SDLs were arranged to scan a simple target made of a watercolor paper printed with three pigmented inks having different absorption spectra. The proper choice of laser wavelengths and feedback levels make easy the unambiguous identification of the pigment under observation by direct comparison of the OF images. 

Figure 5. Graphic abstract of the experimental outcome. The lookup table at bottom-right helps to identify the color distribution on the target. (adapted from Reference [35])

A systematic calibration of the system would allow interpolation and image fusion for quantitative analysis.

5. Unconventional Feedback Imaging

However, 2D detectors, either in form of coupled transverse modes in broad area lasers or independent pixel matrix [36][37][38], are not required to take scanless OF imaging. New computational techniques aimed to the extrapolation of images from low-resolution detectors have reached commercial maturity [39]. Compressed sensing (CS) algorithms allow to reconstruct an N-pixel image taking less than N intensity measurements. CS can be pushed up to the realization of single pixel cameras, which produce spatially resolved images employing a bucket detector. The laser cavity of a single mode semiconductor laser is an inherently single-pixel detector and a scanless OF image can be produced via CS techniques. A proof-of-principle of this approach, as shown in Figure 6. The beam traveling in the OF interferometer is expanded to the size of the target surface and its intensity profile is controlled by a spatial light modulator (SLM). The CS algorithm evaluates the feedback for different intensity profiles and extrapolates an image of the object.

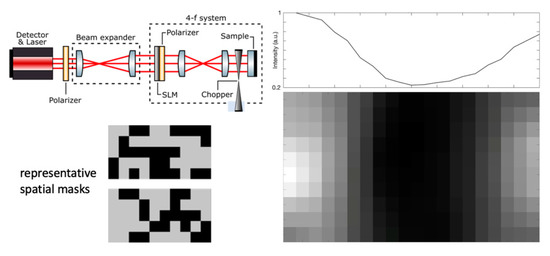
Sensors 20 05930 g013 550

Figure 6. OF scanless image (bottom right) of a metal wire on a mirror surface, taken with the setup sketched at top-left. The OF laser source and detector is an SDL (λ = 670 nm). The spatial-light modulator is taken from a video projector. Total imaged area 2 × 4 mm2. Two representative masks adopted for illuminating the target are shown at bottom-left. The integral over pixel columns of the wire image is shown at top-right (adapted from [40]).

Extension of the CS imaging technology to the mid-infrared and THz wavelengths is far more interesting because of lack of sensitive and affordable 2D detectors in those spectral regions and the stronger stability of QCLs. The spatial resolution of scanless images is partly related to the pixel size of the spatial modulator and partly to the number of implemented masks. Both liquid crystals and micro-mirrors SLMs have relatively large pixels and slow reconfiguration time, thus enforcing a resolution-speed compromise on image quality. Both these limitations could be partly relieved by using optically reconfigurable metasurfaces, especially effective at long wavelength, as demonstrated in Reference [41].

6. Conclusions

Having illustrated the versatility of OF imaging we can anticipate two directions of emerging attentiveness: integrated Si-photonics and in vivo biomedical imaging.

On the one hand, the robustness and flexibility of OF sensors adaptable for kinematic measurements of proximity, deformation, distance, displacement, and velocity, make them interesting for applications in robotics [42]. Innovative OF sensors based on quantum-dot lasers, which are intrinsically more stable than SDLs [43], can be integrated in "all-in-one" Silicon Photonics (SiPh) chips allowing for cascaded or parallel multi-parametric sensing schemes on a single technology.

On the other hand, our understanding of cancer in all tissues indicates that the structure as well as biochemical, mechanical, and functional behavior is altered. No single feature is a diagnostic indicator, but their correlates combined, should enhance the diagnostic power of an examination. Multimodality imaging is the next frontier in early diagnosis and screening, especially in skin and epithelial tissues cancers, which have among the lowest survival rates, if not recognized at their earliest stage. OF imaging has the potential of optically addressing a number of physical parameters characterizing malignant lesions with respect to surrounding tissue and benign lesion [4][21][44].

References

  1. Petermann, K. External optical feedback phenomena in semiconductor lasers. IEEE J. Sel. Top. Quantum. Electron. 1995, 1, 480–489.
  2. Donati, S. Developing self-mixing interferometry for instrumentation and measurements. Laser Phot. Rev. 2012, 6, 393–417.
  3. Taimre, T.; Nikolić, M.; Bertling, K.; Lim, Y.L.; Bosch, T.; Rakić, A.D. Laser feedback interferometry: A tutorial on the self-mixing effect for coherent sensing. Adv. Opt. Photon. 2015, 7, 570–631.
  4. Perchoux, J.; Quotb, A.; Atashkhooei, R.; Azcona, F.J.; Ramírez-Miquet, E.E.; Bernal, O.; Jha, A.; Luna-Arriaga, A.; Yanez, C.; Caum, J.; et al. Current Developments on Optical Feedback Interferometry as an All-Optical Sensor for Biomedical Applications. Sensors 2016, 16, 694.
  5. Rakić, A.D.; Taimre, T.; Bertling, K.; Lim, Y.L.; Dean, P.; Valavanis, A.; Indjin, D. Sensing and imaging using laser feedback interferometry with quantum cascade lasers. Appl. Phys. Rev. 2019, 6, 021320.
  6. Kane, D.M.; Shore, K.A. Unlocking Dynamical Diversity: Optical Feedback Effects on Semiconductor Lasers. John Wiley & Sons Ltd.: Chicherster, UK, 2005.
  7. Jumpertz, L. Nonlinear Photonics in Mid-infrared Quantum Cascade Lasers. Springer International Publishing: Berlin/Heidelberg, Germany, 2017.
  8. Donati, S. Laser interferometry. In Electro-optical instrumentation: Sensing and measuring with lasers. Prentice Hall Professional Technical Reference, Pearson Education, Inc.: Upper Saddle River, NJ, USA, 2004, pp. 89–180.
  9. Bosch, T.; Bès, C.; Scalise, L.; Plantier, G. Optical Feedback Interferometry. In Encyclopedia of Sensors. American Scientific Publishers: Valencia, CA, US, 2006, pp. 1–20.
  10. Ohtsubo, J. Theory of Optical Feedback in Semiconductor Lasers. In Semiconductor Lasers. Stability, Instability and Chaos. Springer-Verlag: Berlin/Heidelberg, Germany, 2017, pp. 83–112.
  11. Brunner, D.; Luna, R.; Delhom i Latorre, A.; Porte, X.; Fischer, I. Semiconductor laser linewidth reduction by six orders of magnitude via delayed optical feedback. Opt. Lett. 2017, 42, 163–166.
  12. Locquet, A. Routes to chaos of a semiconductor laser subjected to external optical feedback: A review. Photonics 2020, 7, 22.
  13. Giuliani, G.; Norgia, M.; Donati, S.; Bosch, T. Self-Mixing Technique for Sensing Applications. J. Optics A 2002, 4, 283–294.
  14. Lui, H.S.; Taimre, T.; Bertling, K.; Lim, Y.L.; Dean, P.; Khanna, S.P.; Lachab, M.; Valavanis, A.; Indjin, D.; Linfield, E.H.; et al. Terahertz inverse synthetic aperture radar imaging using self-mixing interferometry with a quantum cascade laser. Opt. Lett. 2014, 39, 2629–2632.
  15. Giordano, M.C.; Mastel, S.; Liewald, C.; Columbo, L.L.; Brambilla, M.; Viti, L.; Politano, A.; Zhang, K.; Li, L.; Davies, A.G.; et al. Phase-resolved terahertz self-detection near-field microscopy. Opt. Expr. 2018, 26, 18423–18435.
  16. Ehtesham, A.; Zabit, U.; Bernal, O.D.; Raja, G.; Bosch, T. Analysis and Implementation of a Direct Phase Unwrapping Method for Displacement Measurement Using Self-Mixing Interferometry. IEEE Sens. J. 2017, 17, 7425–7432.
  17. Giuliani, G.; Bozzi-Pietra, S.; Donati, S. Self-mixing laser diode vibrometer. Meas. Sci. Technol., 2002, 14, 24.
  18. Ottomaniello, A.; Keeley, J.; Rubino, P.; Li, L.; Cecchini, M.; Linfield, E.H.; Davies, A.G.; Dean, P.; Pitanti, A.; Tredicucci, A. Optomechanical response with nanometer resolution in the self-mixing signal of a terahertz quantum cascade laser. Opt. Lett. 2019, 44, 5563–5666.
  19. Donati, S.; Rossi, D.; Norgia, M. Single Channel Self-Mixing Interferometer Measures Simultaneously Displacement and Tilt and Yaw Angles of a Reflective Target. IEEE J. Quantum Electron. 2015, 51, 1–8.
  20. Zabit, U.; Shaheen, K.; Naveed, M.; Bernal, O.D.; Bosch, T. Automatic Detection of Multi-Modality in Self-Mixing Interferometer. IEEE Sens. J. 2018, 18, 9195–9202.
  21. Mowla, A.; Bertling, K.; Wilson, S.J.; Rakić, A.D. Dual-Modality Confocal Laser Feedback Tomography for Highly Scattering Medium. IEEE Sens. J. 2019, 19, 6134–6140.
  22. Lang, R.; Kobayashi, K. External optical feedback effects on semiconductor injection laser properties. IEEE J. Quantum Electron. 1980, 16, 347–355.
  23. Tkach, R.W.; Chraplyvy, A.R. Regimes of feedback effects in 1.5 μm distributed feedback laser. IEEE J. Light. Technol. 1986, LT-4, 1655–1661.
  24. Acket, G.A.; Lenstra, D.; den Boef, J.; Verbeek, B.H. The influence of feedback intensity on longitudinal mode properties and optical noise in index guided semiconductor lasers. IEEE J. Quant. Electron. 1984, 20, 1163–1169.
  25. Henry, C.H. Theory of the linewidth of semiconductor lasers. IEEE J. Quant. Electron. 1982, 18, 259–264.
  26. Dean, P.; Valavanis, A.; Keeley, J.; Bertling, K.; Lim, Y.L.; Alhathlool, R.; Chowdhury, S.; Taimre, T.; Li, L.H., Indjin, D.; et al. Coherent three-dimensional terahertz imaging through self-mixing in a quantum cascade laser. Appl. Phys. Lett. 2013, 103, 181112.
  27. Mezzapesa, F.P.; Petruzzella, M.; Dabbicco, M.; Beere, H.E.; Ritchie, D.A.; Vitiello, M.S.; Scamarcio, G. Continuous-wave reflection imaging using optical feedback interferometry in Terahertz and mid-infrared quantum cascade lasers. IEEE Trans. Terahertz Sc. Tech. 2014, 4, 631–634.
  28. Dabbicco, M.; Colafemmina, G. Multi-wavelength imaging of tissue phantoms by optical feedback interferometry. In Nanoscale Imaging, Sensing, and Actuation for Biomedical Applications XVI, Proceedings of the SPIE n. 10891, San Francisco, CA, USA, 2–7 february 2019; International Society for Optics and Photonics: Bellingham, WA, USA, 2019.
  29. Tucker, J.R.; Rakić, A.D.; O’Brien, C.J.; Zvyagin, A.V. Effect of multiple transverse modes in self-mixing sensors based on vertical-cavity surface-emitting lasers. Appl. Opt. 2007, 46, 611–619.
  30. Dai, X.; Wang, M.; Zhou, C. Multiplexing Self-Mixing Interference in Fiber Ring Lasers. IEEE Photon. Technol. Lett. 2010, 22, 1619–1621.
  31. Zhang, S.; Zhang, S.; Tan, Y.; Sun, L. Self-mixing interferometry with mutual independent orthogonal polarized light. Opt. Lett. 2016, 41, 844–846.
  32. Columbo, L.L.; Brambilla, M.; Dabbicco, M.; Scamarcio, G. Self-mixig in multi-transverse mode semiconductor lasers: Model and potential application to multiparametric sensing. Opt. Expr. 2012, 20, 6286–6305.
  33. Columbo, L.L.; De Lucia, F.; Brambilla, M.; Dabbicco, M. Self-mixing in VCSELs for multi-parametric sensing applications: Theory and experiment. In Semiconductor Laser and Laser Dynamics V; Proceedings of SPIE n. 8432, Brussels, Belgium, 16–19 April 2012; International Society for Optics and Photonics: Bellingham, WA, USA, 2012.
  34. Dabbicco, M.; Maggipinto, T.; Brambilla, M. Optical bistability and stationary patterns in photonic-crystal vertical-cavity surface-emitting lasers. Appl. Phys. Lett. 2005, 86, 0211116.
  35. Kao, T.; Reno, J.; Hu, Q. Phase-locked laser arrays through global antenna mutual coupling. Nature Photon. 2016, 10, 541–546.
  36. Orenstein, M.; Kapon, E.; Stoffel, N.G.; Harbison, J.P.; Florez, L.T.; Wullert, J. Two-dimensional phase-locked arrays of vertical-cavity semiconductor lasers by mirror reflectivity modulation. Appl. Phys. Lett. 1991, 58, 804–806.
  37. Lim, Y.L.; Nikolic, M.; Bertling, K.; Kliese, R.; Rakić, A.D. Self-mixing imaging sensor using a monolithic VCSEL array with parallel readout. Opt. Expr. 2009, 17, 5517–5525.
  38. Lee, B.G.; Belkin, M.A.; Pflugl, C.; Diehl, L.; Zhang, H.A.; Audet, R.M.; MacArthur, J.; Bour, D.P.; Corzine, S.W.; Hofler, G.E.; et al. DFB Quantum Cascade Laser Arrays. IEEE J. Quantum Electron. 2009, 45, 554–565.
  39. Rani, M.; Dhok, S.B.; Deshmukh, R.B. A Systematic Review of Compressive Sensing: Concepts, Implementations and Applications. IEEE Access 2018, 6, 4875–4894.
  40. Lupo, A.; Sylos Labini, P.; Dabbicco, M. Scanless and detectorless imaging by optical feedback interferometry. In Proceedings of Frontiers in Optics + Laser Science APS/DLS, (2020) accepted for publication.
  41. Mezzapesa, F.P.; Columbo, L.L.; Rizza, C.; Brambilla, M.; Ciattoni, A.; Dabbicco, M.; Vitiello, M.S.; Scamarcio, G. Photo-designed metamaterials induce modulation of CW terahertz quantum cascade lasers. Sci. Rep. 2015, 5, 16207.
  42. Shnitser, P.; Miller, D.; Ulmer, C.T.; Romanov, V.; Grubsky, V. Robotic autonomous navigation and orientation tracking system and methods. Patent US10207410B1, 7 January 2019.
  43. O’Brien, D.; Hegarty, S.P.; Huyet, G.; Uskov, A.V. Sensitivity of quantum-dot semiconductor lasers to optical feedback. Opt. Lett. 2004, 29, 1072–1074.
  44. Donati, S.; Norgia, M. Self-Mixing Interferometry for Biomedical Signals Sensing. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 104–111.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Optics
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Massimo Brambilla
,
Lorenzo Luigi Columbo
,
Maurizio Dabbicco
,
Francesco De Lucia
,
Francesco Paolo Mezzapesa
,
Gaetano Scamarcio
View Times: 625
Revisions: 2 times (View History)
Update Date: 18 Nov 2020
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback