1000/1000
Hot
Most Recent

We discuss the concept of trade competition and review the fundamental measures recently introduced in the literature to capture this concept in empirical terms. To that end, a modified version of the Krugman index is taken as starting point.
The remarkable growth of international trade in the last decades is one of the most significant dimensions of globalization. It is now a matter of fact that the world is increasingly interdependent and that the different countries are more open[1][2]. At the same time, new poles emerge in the international arena. This complex new context leads to stronger levels of trade competition among the different countries aiming to obtain higher market shares.
The standard approach to evaluate trade competition makes use of the concept of structural similarity[3][4][5]. This can be captured through a one-dimensional or through a multi-dimensional index.
Several alternative measures can be used to quantify the level of structural similarity between two countries (and, therefore, the level of trade competition between them). Nicole Palan[6] provides an interesting survey on this regard. Among the most commonly applied indexes, we can mention the Krugman specialization index[7] or the Finger-Kreinin index[8].
Let us assume the Krugman index as reference. We represent the exporting countries under analysis through the indexes i (i = 1, 2, …,I) and h (h = 1, 2, …, H). Additionally, j is the sectoral index (j = 1, 2, …,J). The destination market is represented by p. The standard version of the Krugman index compares the share of each sector in two export structures and can be expressed as follows:
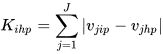 (1)
(1)
in which 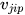 is the share of sector j in the exports from i to p. The same applies to
is the share of sector j in the exports from i to p. The same applies to 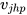 which represents the share of sector j in the exports from h to p. This measure ranges between 0 (perfect similarity) and 2 (perfect dissimilarity). Thus, the higher the level of structural similarity the lower the index. Moreira et al.[4] argue that these characteristics are counter-intuitive. In order to overcome this problem, they introduce two small adjustments in the Krugman index. The new version is as follows:
which represents the share of sector j in the exports from h to p. This measure ranges between 0 (perfect similarity) and 2 (perfect dissimilarity). Thus, the higher the level of structural similarity the lower the index. Moreira et al.[4] argue that these characteristics are counter-intuitive. In order to overcome this problem, they introduce two small adjustments in the Krugman index. The new version is as follows:
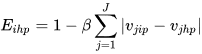 (2)
(2)
Assuming β=0.5, 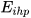 ranges between 0 and 1. The level of structural similarity reaches its maximum value when
ranges between 0 and 1. The level of structural similarity reaches its maximum value when 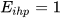 . This case corresponds to the maximum level of trade competition between i and h. It is interesting to note that this one-dimensional approach only takes into account the weights of each sector in the exports of both countries to p.
. This case corresponds to the maximum level of trade competition between i and h. It is interesting to note that this one-dimensional approach only takes into account the weights of each sector in the exports of both countries to p.
Based on 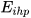 , Crespo and Simoes[3] argue that two new dimensions can be added to the analysis. Therefore, a multi-dimensional analysis of trade competition can consider not only the weights of the sectors but also: (i) the level of inter-sectoral similarity; (ii) the level of intra-sectoral similarity. Let us consider both extensions.
, Crespo and Simoes[3] argue that two new dimensions can be added to the analysis. Therefore, a multi-dimensional analysis of trade competition can consider not only the weights of the sectors but also: (i) the level of inter-sectoral similarity; (ii) the level of intra-sectoral similarity. Let us consider both extensions.
Starting with inter-sectoral similarity, Crespo and Simoes[3] make use of the different levels of sectoral disaggregation that comprise a specific statistical nomenclature (for example, the Combined Nomenclature). Then, they obtain the weighted average of the structural similarity indexes calculated at each level of sectoral disaggregation (being these levels represented by 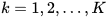 ), with the weight of each level given by
), with the weight of each level given by 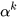 :
:
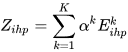 (3)
(3)
where 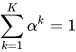 . The indexes
. The indexes 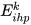 are calculated as in equation (2), for each level k.
are calculated as in equation (2), for each level k.
Obviously, the concrete values of 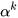 are (arbitrarily) fixed by the researcher. The sum of these values is 1.
are (arbitrarily) fixed by the researcher. The sum of these values is 1.
The other possible extension is, as mentioned above, the inclusion of the intra-sectoral similarity in the analysis. This is important because there is strong support in the literature for the existence of remarkable intra-sectoral differences between the countries[4]. The incorporation of this dimension obviously requires the measurement of the quality of the goods. As suggested by Stiglitz[9], the unit export values can be used as proxy for quality. In terms of measurement, it is necessary to analyse, for each sector, the difference between the quality level of the exports of countries i and h. This can be done as follows:
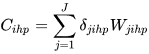 (4)
(4)
in which, in its simplest version:
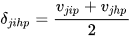 (5)
(5)
and
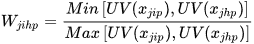 . (6)
. (6)
For each sector j, 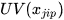 and
and  correspond to the unit values of the exports from i and h to
correspond to the unit values of the exports from i and h to 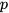 , respectively. Therefore,
, respectively. Therefore, 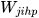 corresponds to the ratio between the minimum of these two values and the maximum one. A value closer to 1 means a stronger similarity in terms of quality ranges exported.
corresponds to the ratio between the minimum of these two values and the maximum one. A value closer to 1 means a stronger similarity in terms of quality ranges exported.
It is easy to verify that 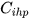 is an adjustment factor that reduces the degree of structural similarity between and according to the average degree of intra-sectoral dissimilarity[5].
is an adjustment factor that reduces the degree of structural similarity between and according to the average degree of intra-sectoral dissimilarity[5].