
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Michael H. Spiegel | + 1514 word(s) | 1514 | 2020-09-09 16:27:18 | | | |
| 2 | Felix Wu | Meta information modification | 1514 | 2020-10-26 04:12:31 | | |
Video Upload Options
Multi-microgrids address the need for a resilient, sustainable, and cost-effective electricity supply by providing a coordinated operation of individual networks. Due to local generation, dynamic network topologies, and islanding capabilities of hosted microgrids or groups thereof, various new fault mitigation and optimization options emerge. However, with the great flexibility, new challenges such as complex failure modes that need to be considered for a resilient operation, appear. Multi-Microgrid scheduling refers to the procedure of jointly controlling the assets in a multi-microgrid such that the potential of multi-microgrids can be leveraged.
1. Introduction
Several decades ago, electrical networks called microgrids that can be both operated in a grid-connected and islanded mode were established. Such networks are often constructed to meet advanced power quality and reliability requirements which cannot be achieved by the main grid alone. Additional incentives include the economic interest in a tight integration of Renewable Energy Sources (RES), lowered purchase costs, as well as an increased efficiency by local generation [1]. Since the introduction of microgrids, several topics ranging from low-level voltage and frequency control up to high-level economic and reliable operation schedules of microgrid assets have been addressed [2][3].
A few years ago, the concept of multi-microgrids was introduced and has since attracted attention [4][5][6]. In most cases, multi-microgrids are defined as power systems, which incorporate multiple coordinated microgrids. Main driving forces in implementing multi-microgrids include resilience enhancements by supplying microgrid-external loads in case of contingencies as well as economic performance gains by sharing backup capacity and jointly optimizing normal operation. Following the diverse incentives and requirements, various multi-microgrid network topologies and coordination schemes [7] were presented. For instance, several microgrids can be connected via a common distribution system and a high-level controller may coordinate a jointly islanded operation of multiple connected microgrids in case the upstream grid fails. Furthermore, the distribution system may be split into multiple separate islands that are powered by connected microgrids within the island to circumvent distribution system faults. However, sharing backup capacity, in particular, requires a grid operation as one single or many parallel unconnected islands, which is not feasible in standard distribution systems.
An exemplary multi-microgrid is depicted in Figure 1. Each of the three individual microgrids consists of various assets, such as controllable Distributed Energy Resources (DERs), energy storage units, volatile RES, and mixed-critical loads that may or must be supplied in case of contingencies. A deployed scheduling algorithm needs to control the microgrid assets before any contingency such that a resilient and cost-effective operation is achieved. A conventional scheduler, although it may consider the inherent stochasticity of loads, RES, and main-grid failures, may not consider the weak line L2-3. Even though the multi-microgrid can successfully tolerate main-grid outages, tripping L1-3 may cause an overload of the weak line L2-3 in case the power exchange between MG3 and the other microgrids exceeds the line capacity. To circumvent this situation, more generation needs to be scheduled at MG3, locally.
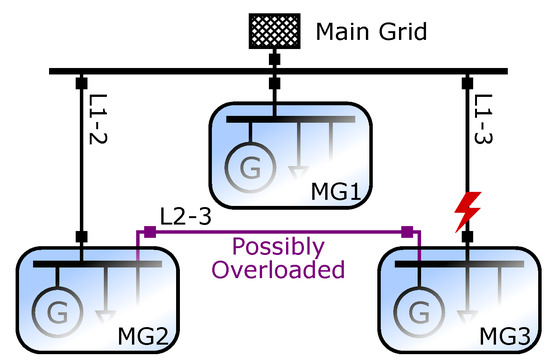
Figure 1. Exemplary multi-microgrid.
2. Work Related to a Resilient and Economic Multi-Microgrid Operation
Substantial work has been contributed in related microgrid topics such as scheduling resources in microgrids, multi-microgrid forming and analyzing failure scenarios in power grids. Additionally, several contributions target the complexity of optimal asset scheduling in systems which face various sources of uncertainty (e.g., induced by volatile RES). At the same time, the approaches ensure that the microgrids can withstand certain failures [2][8].
2.1. Failure Modes and Resilience Metrics
Despite the lack of a common definition of resilience in the context of power systems [9][10][11][12], some properties such as the ability to withstand and to recover from disruptive events are regularly associated with the term [8]. For instance, [10] that studies the definition of resilience in detail, defined the term with respect to an unexpected set of disturbances as “the system’s ability to reduce the magnitude and duration of the disruption”. The related term robustness is declared as “the ability of a system to cope with a given set of disturbances and maintain its functionality” [10]. A resilient system is associated with the ability of downgrading the performance while a robust one maintains the desired performance in the presence of potentially disruptive events. A review of 12 resilience definitions is given in [9]. The authors noted that in addition to restoration aspects, several definitions also include the avoidance of degraded states that others associate with robustness, only [12].
One attempt towards a common definition of power system resilience was made in [11] which relates resilience to various other terms such as reliability and robustness. Reliability, i.e., the probability of a functional system, reflects the performance under given conditions and over a long period of time, while resilience emphasizes the time-varying conditions in a contained time frame. The authors concluded that new metrics are needed to reflect resilience and presented a generalized framework to define such metrics. Similarly, a framework for resilience metrics is proposed in [12], which considers resilience as a function of time that reflects the recovery from a disruptive event. The framework was applied to assess the resilience of a road network.
Special attention must be drawn to the definition of considered failure modes. To secure the operation of conventional power systems, often the (N−1)
robustness criterion—which states that an operation strategy has to withstand the outage of any single system component—is applied [4]. Nevertheless, more detailed failure scenarios and other reliability indices may be used as well to secure the operation of microgrids and multi-microgrids. For instance, fault tree analysis, a method which is commonly used in risk assessment, was applied in [13] to identify critical components and to estimate the reliability of microgrids.
To assess the reliability of isolated microgrids without the need for a detailed stochastic characterization of volatile energy sources, [14] uses easily available capacity factors to approximate various reliability metrics. Alternative assessment strategies include Monte-Carlo-based methods, which sample a large number of scenarios to approximate the joint distribution of all uncertainties [15]. Although these methods primarily target robustness and reliability aspects, they may also be incorporated into scheduling problems to improve the resilience of a particular schedule.
2.2. Resilience-Aware Microgrid Scheduling
A solution for the economic dispatch problem in single microgrids that ensures a stable islanded operation was presented in [16]. The authors considered the effects of the primary control strategy on the scheduling decision in detail, but only static security margins were used to reflect forecasting errors. To guarantee that critical loads can be supplied in islanded mode, Ref. [17] presented a scheduling method that is based on robust optimization. One deterministic worst-case scenario is found to define the resilient operation. An optimal normal operation schedule is revised in case it lacks sufficient online capacity for switching to an islanded operation. Hussain et al. [18] studied scheduling in multi-microgrids and proposed a robust optimization-based approach to incorporate inherent uncertainties. Although they also considered the islanded operation schedule, no detailed physical network model and no grid-reconfiguration options are included.
Some work also directly deploys stochastic optimization. For instance, in [19], a two-stage stochastic optimization approach that takes various network constraints and the required spinning reserve into account was presented. The expected cost under the presence of stochastic phenomena was optimized by mapping the problem into a deterministic linear optimization. Demand-response actions in a stochastic scheduling problem were studied in [20]. The presented approach also considers reserve requirements for compensating fluctuations.
2.3. Multi-Microgrid Forming
Conventional outage management systems are designed to automatically locate faults and restore healthy portions of a distribution grid [21] but an islanded operation is rarely considered. The role of microgrids in enhancing resilience was highlighted in [22], which describes the option that these microgrids provide surplus power to restore parts of the distribution grid. A particular method to control the supply of external loads was presented in [23] considering that the time loads can be expectedly supplied with available energy reserves.
A Mixed Integer Linear Programming (MILP) formulation of the grid partitioning problem, which forms each radial partition by a single generator, is additionally given in [24]. Supplied loads are maximized and switching operations are minimized in [25] by partitioning healthy but islanded sections of distribution networks into self-sustainable microgrids. Although some of the outlined approaches study both normal and emergency operation, the impact of grid-reconfiguration options on local reserve requirements in normal operation mode is not considered. Nevertheless, presented fault mitigation and reconfiguration options may be used to refine reserve estimation in asset scheduling problems.
2.4. Resilience-Aware Multi-Microgrid Scheduling
Some work specifically targeting resilience-aware scheduling in multi-microgrid environments is already available. To reduce the high share of dispatchable DERs, the concept of provisional microgrids, i.e., less critical microgrids that rely on other microgrids for islanding, was introduced [26]. Notably, an uncertainty-constrained optimal scheduling model that also includes islanding constraints is given. In particular, the concept and formulation of provisional microgrids may be used in the planned work as well. A risk-based model of optimal energy exchange scheduling between networked microgrids is given in [27]. Multiple strategies to deal with inherent risks connected to the stochastic nature of load and generation are presented and evaluated. The presented risk measure may be as well applied to manage risks in other multi-microgrid setups that cover an extended range of failure scenarios.
References
- Marnay, C.; Abbey, C.; Joos, G.; Ash, K.; Bando, S.; Braun, M.; Chatzivasileiadis, S.; Driesen, J.; Hatziargyriou, N.; Iravani, R.; et al. Microgrids 1 Engineering, Economics, & Experience–Capabilities, Benefits, Business Opportunities, and Examples; Technical report; WG C6.22; CIGRÉ: Paris, France, 2015.
- Parhizi, S.; Lotfi, H.; Khodaei, A.; Bahramirad, S. State of the Art in Research on Microgrids: A Review. IEEE Access 2015, 3, 890–925.
- Hussain, A.; Bui, V.H.; Kim, H.M. Microgrids as a resilience resource and strategies used by microgrids for enhancing resilience. Appl. Energy 2019, 240, 56–72.
- Gholami, A.; Aminifar, F.; Shahidehpour, M. Front Lines Against the Darkness: Enhancing the Resilience of the Electricity Grid Through Microgrid Facilities. IEEE Electrif. Mag. 2016, 4, 18–24.
- Hatziargyriou, N. (Ed.) Microgrids: Architectures and Control; John Wiley & Sons: West Sussex, UK, 2014.
- Kariniotakis, G.; Martini, L.; Caerts, C.; Brunner, H.; Retiere, N. Challenges, innovative architectures and control strategies for future networks: The Web-of-Cells, fractal grids and other concepts. In Proceedings of the 24th International Conference & Exhibition on Electricity Distribution (CIRED), Glasgow, UK, 12–15 June 2017.
- Bullich-Massagué, E.; Díaz-González, F.; Aragüés-Peñalba, M.; Girbau-Llistuella, F.; Olivella-Rosell, P.; Sumper, A. Microgrid clustering architectures. Appl. Energy 2018, 212, 340–361.
- Aftab Ahmad Khan; Muhammad Naeem; Muhammad Iqbal; Saad Qaisar; A. Anpalagan; A compendium of optimization objectives, constraints, tools and algorithms for energy management in microgrids. Renewable and Sustainable Energy Reviews 2016, 58, 1664-1683, 10.1016/j.rser.2015.12.259.
- Shirzadi, S.; Nair, N.K.C. Power system resilience through microgrids: A comprehensive review. In Proceedings of the 2018 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Kota Kinabalu, Malaysia, 7–10 October 2018.
- Arghandeh, R.; von Meier, A.; Mehrmanesh, L.; Mili, L. On the definition of cyber-physical resilience in power systems. Renew. Sustain. Energy Rev. 2016, 58, 1060–1069.
- Gholami, A.; Shekari, T.; Amirioun, M.H.; Aminifar, F.; Amini, M.H.; Sargolzaei, A. Toward a consensus on the definition and taxonomy of power system resilience. IEEE Access 2018, 6, 32035–32053.
- Henry, D.; Ramirez-Marquez, J.E. Generic metrics and quantitative approaches for system resilience as a function of time. Reliab. Eng. Syst. Saf. 2012, 99, 114–122.
- Li, Z.; Yuan, Y.; Li, F. Evaluating the reliability of islanded microgrid in an emergency mode. In Proceedings of the 2010 45th International Universities Power Engineering Conference (UPEC), Wales, UK, 31 August–3 September 2010.
- Falahati, B.; Kargarian, A.; Fu, Y. Timeframe capacity factor reliability model for isolated microgrids with renewable energy resources. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012.
- Bie, Z.; Zhang, P.; Li, G.; Hua, B.; Meehan, M.; Wang, X. Reliability evaluation of active distribution systems including microgrids. IEEE Trans. Power Syst. 2012, 27, 2342–2350.
- Ahn, S.J.; Nam, S.R.; Choi, J.H.; Moon, S.I. Power scheduling of distributed generators for economic and stable operation of a microgrid. IEEE Trans. Smart Grid 2013, 4, 398–405.
- Khodaei, A. Resiliency-oriented microgrid optimal scheduling. IEEE Trans. Smart Grid 2014, 5, 1584–1591.
- Hussain, A.; Bui, V.H.; Kim, H.M. Robust optimization-based scheduling of multi-microgrids considering uncertainties. Energies 2016, 9, 278.
- Gholami, A.; Shekari, T.; Aminifar, F.; Shahidehpour, M. Microgrid Scheduling With Uncertainty: The Quest for Resilience. IEEE Trans. Smart Grid 2016, 7, 2849–2858.
- Zakariazadeh, A.; Jadid, S.; Siano, P. Smart microgrid energy and reserve scheduling with demand response using stochastic optimization. Int. J. Electr. Power Energy Syst. 2014, 63, 523–533.
- Jayantilal, A.; McCarthy, C.A. Reducing Customer Outages–Smart Distribution through Layered Intelligence. NEMA Electroind. Mag. 2012, 3, 1170–1180.
- Che, L.; Khodayar, M.; Shahidehpour, M. Only connect: Microgrids for distribution system restoration. IEEE Power Energy Mag. 2014, 12, 70–81.
- Gao, H.; Chen, Y.; Xu, Y.; Liu, C.C. Resilience-oriented critical load restoration using microgrids in distribution systems. IEEE Trans. Smart Grid 2016, 7, 2837–2848.
- Chen, C.; Wang, J.; Qiu, F.; Zhao, D. Resilient distribution system by microgrids formation after natural disasters. IEEE Trans. Smart Grid 2016, 7, 958–966.
- Kimble, S.J.; Vedullapalli, D.T.; Makram, E.B. Optimal Partitioning of Distribution Networks for Micro-Grid Operation. J. Power Energy Eng. 2017, 5, 104–120.
- Khodaei, A. Provisional microgrids. IEEE Trans. Smart Grid 2015, 6, 1107–1115.
- Gazijahani, F.S.; Ravadanegh, S.N.; Salehi, J. Stochastic multi-objective model for optimal energy exchange optimization of networked microgrids with presence of renewable generation under risk-based strategies. ISA Trans. 2018, 73, 100–111.




