
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Gennaro Pescitelli | + 3521 word(s) | 3521 | 2019-05-21 12:44:56 | | | |
| 2 | Rita Xu | Meta information modification | 3521 | 2020-05-14 08:33:28 | | | | |
| 3 | Bruce Ren | -61 word(s) | 3460 | 2020-10-29 09:20:35 | | | | |
| 4 | Gennaro Pescitelli | Meta information modification | 3460 | 2021-11-17 16:42:05 | | | | |
| 5 | Gennaro Pescitelli | Meta information modification | 3460 | 2022-05-24 16:53:11 | | |
Video Upload Options
This entry provides an introduction to the basic concepts of Electronic Circular Dichroism (ECD) spectroscopy. It describes the fundamental principles, instrumentation, and different approaches for interpreting and predicting ECD spectra. It surveys the most popular modern applications of ECD for the structural analysis of organic compounds.
1. Introduction
Circular dichroism (CD) is defined as the differential absorption of left- and right-circularly polarized electromagnetic radiation by a sample. In particular, electronic circular dichroism (ECD, often shortened itself as CD) occurs in correspondence with electronic transitions and represents the chiroptical counterpart of the more common UV-vis absorption spectroscopy. Similarly, other chiroptical spectroscopies such as vibrational CD (VCD), Raman optical activity (ROA), circularly polarized luminescence (CPL), and so on, all have their counterparts in infrared (IR), Raman and fluorescence spectroscopies, respectively. The main advantage of using chiroptical spectroscopies instead of their non-chiral counterparts is that the former, but not the latter, are sensitive to the absolute configuration of a sample. In simple words, while the two enantiomers of a chiral substance, for instance (+) and (-)-camphor, will have identical UV-vis, IR and Raman spectra, they will have distinguishable, mirror-image looking, ECD, VCD and ROA spectra (Figure 1). Moreover, chiroptical spectroscopies are more sensitive toward the overall molecular structure than their non-chiral counterpart. Any ECD or VCD or ROA spectrum contains a lot of structural information about the molecular structure, in terms of both conformation and configuration, although it not always easy to find robust and practical means to extract such the information from the spectra.[1]
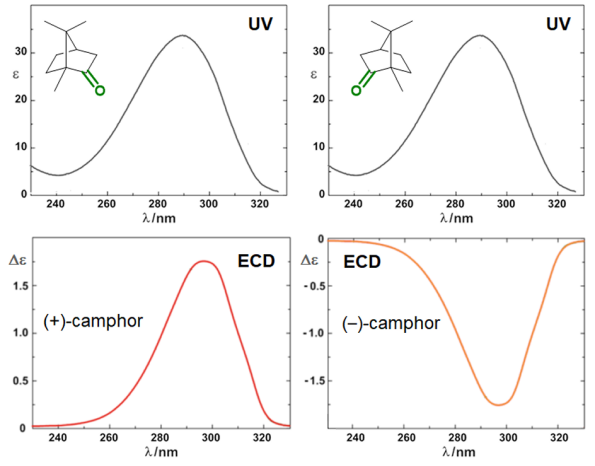
Figure 1. UV-vis absorption and ECD spectra of camphor enantiomers.
2. Basics
2.1 Phenomenological and theoretical aspects
Let A be the absorption of a sample of isotropic (non-polarized) light, and AL and AR the absorptions of left and right circularly polarized light (L- and R-CPL). The CD is then written as:

This quantity is usually measured in mdeg units. To define a molar quantity Δε, expressed in the same units M–1cm–1 of molar extinction coefficient ε, an analogous of Lambert and Beer’s expression is used:
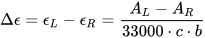
Δε is now independent of the concentration c, expressed in M, and of the cell path-length b, expressed in cm.
Non-negligible CD signals (a CD band is also called a Cotton effect) can be measured only in correspondence to absorption bands, i.e., when resonance occurs in light/matter interaction. This usually involves either electronic or vibrational transitions, therefore the useful ranges for CD measurements are the UV-vis (ECD) and the IR one (VCD and ROA). The ratio between CD and absorption intensity is defined through the so-called anisotropy or dissymmetry g-factor

which is a pure number, independent of concentration or path-length. Focusing on ECD, common g-values are in the 10–5-10–3 range. In fact, CD spectroscopy, bieng by definition a difference spectroscopy, is intrinsically poorly sensitive in terms of signal intensity. From the definition it is also clear that Δε may assume positive or negative values, and in fact the CD spectra of two enantiomers are the mirror image (with respect to the x-axis) of each other (see Figure 1 for camphor).
CD is related to a quantum-mechanical quantity called rotational strength, defined as the dot product between the electric and magnetic transition moments allied to an electronic transition from the ground electronic state 0 to an excited electronic state i
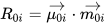
Symmetry restrictions imply that R may be non-negligible only for molecules belonging to symmetry groups devoid of roto-reflection elements, i.e., of inversion centers and symmetry planes. Therefore, only chiral systems may exhibit CD. The integral of a CD band allied with a single electronic transition is related to the rotational strength through:
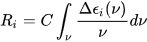
where C is a numerical constant equal to 2.296·10–39 cgs units. Conversely, a CD spectrum may be thought to amount to a sum of bands with intensity proportional to their respective rotational strengths, each occurring at a defined frequency corresponding to the 0→i electronic transition:
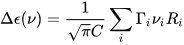
where Γi is the appropriate band-shape function (for instance, a Gaussian or Lorentzian band)[2] centered at νi (it also contains a band-width quantity σi).
2.2 Instrumentation and sample preparation
A standard benchtop ECD spectropolarimeter has the same instrumental design as a common spectrophotometer with a few differences (Figure 2).[3] The incident radiation coming from a source (S) must be circularly polarized, which is achieved through a photoelastic modulator (PEM) placed after the monochromator (M). The PEM produces L- and R-CPL alternately with a frequency of 50 KHz. The transmitted light is thus modulated at the same frequency, the average of the two signals being proportional to A and their difference to CD. This latter must be amplified and the two signals recombined (through a lock-in amplifier) to output the true ECD signal collected by the photomultiplier (PMT). Similarly to UV-vis spectroscopy, the usual range for ECD measurements is between 185 and 700 nm. While extension to longer wavelengths (toward the near IR region) is easily accessible, that to shorter wavelengths requires a very special apparatus (vacuum and synchrotron sources). Samples are usually solutions contained in cylindrical quartz cells with path-lengths ranging from 0.01 to 1 cm. Suitable solvents must be transparent in the near UV-vis region, that is, have relatively low wavelength cut-off, such as water, methanol, acetonitrile, dioxane and hexane. Sample concentrations must be chosen, similarly to absorption spectroscopy, so not to exceed 0.8-1 absorbance units in the observed range. For a compound with a maximum extinction coefficient ε ≈ 104, one would need to prepare a solution with concentration ≈ 1 mM, to be measured with a 0.1 cm cell. Normally, solutions with ≈ 1 mg/mL concentration or less can be measured by ECD, with a proper choice of the cell. ECD spectra can also be recorded on solid samples, for examples microcrystals disperded in an inert salt matrix, thin films deposited on quartz windows, and gels.
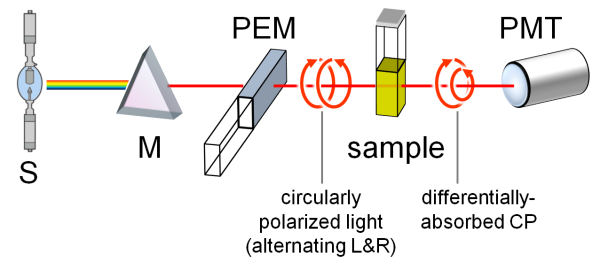 Figure 2. Schematic reprentation of a ECD spectropolarimeter.
Figure 2. Schematic reprentation of a ECD spectropolarimeter.
3. Structure-to-spectra relationship
3.1 Chromophores and perturbers
A fundamental prerequisite to observe ECD signals is the presence of one or more chromophores like those depicted in Figure 3. A chromophore is a unit or fragment composed of one or more atoms responsible for the occurrence of one or more electronic transitions. A chromophore is for a spectroscopic something similar to what a functional group is for an organic chemist. Useful chromophores absorbing in the UV-vis region are either moieties containing a conjugated π-system or atoms with high-energy non-bonding orbitals, which undergo n-π*, n-σ* and π-π* transitions, or a metal ion undergoing d-d transitions. Normally, only the transitions to the lowest-lying excited electronic states are detected. For π-conjugated systems, the true chromophore extends over all atoms with pπ atomic orbitals taking part to the π clouds. For example, for a dimethylaminobenzoate the chromophore will include at least the ring carbons, the carboxyl moiety and the nitrogen.
All chromophores shown in Figure 3 are planar and intrinsically achiral. However, when embedded in a chiral entity, either a molecule or a supramolecular adduct, they feel (or are perturbed by) the environment and their otherwise ECD-silent transitions become ECD-active. A chiral "environment" may be provided by a non-chromophoric chiral skeleton which “perturbs” the chromophore, or by a second chromophoric group interacting with the first one.[4]
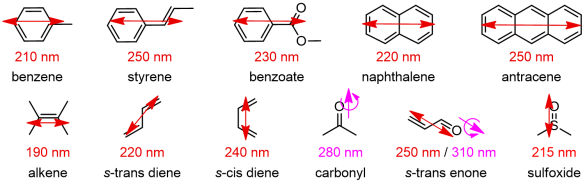
Figure 3. Common organic chromophores with their main UV electronic transitions;
electric transition dipoles shown as double arrows, magnetic as single plus curved arrows.
3.2 Conformation and configuration
Since the ECD spectra of two enantiomeric compounds are the mirror image of each other, the first and most immediate information one looks for in a ECD spectrum is its sign, which is related to the absolute configuration of the sample. Any ECD spectrum – in terms of both sign and shape – is however also sensitive to the molecular conformation. It may happen in fact that two different conformations of the same chiral molecule (with defined configuration) are associated with mirror-image ECD spectra.[5]
Therefore, almost every aspect of a ECD spectrum depends on a combination of conformational and configurational factors.[6] As a consequence, when ECD spectra are used to assign absolute configurations, the molecular conformation(s) responsible for the observed ECD should be known with accuracy and possibly by independent techniques, i.e. calculations or NMR spectroscopy or, better, a combination thereof. However, ECD lends itself as a tool for investigating conformations as well, most likely as a complement to NMR.[7]
3.3 Eliciting structures through ECD spectra: strategy outline
Depending on whether one wants to investigate by ECD the absolute cconfiguration or the conformation, the general strategy used in the analysis is different.
To assign absolute configurations, the normal way to proceed is the following.[8]
1. Investigate the molecular conformation in solution or in the solid-state, depending if the experimental ECD has been recorded in solution or on a solid sample. In the first case, if the compound is moderately flexible, several low-energy conformations may be populated at room (or the working) temperature. They need to be studied by a combination of computational and spectroscopical means. In the second case, the structure found e.g. by means of X-ray must be considered.
2. Assume an initially arbitrary absolute configuration.
3. For each relevant structure, estimate a portion of the expected ECD spectrum by some means (see section "Predictions of ECD spectra").
4. If only a single structure is important, e.g. for very rigid compounds or in the solid crystalline state, compare the expectation with the experimental ECD.
5. If several different conformations contribute to the observed ECD spectrum, all of them must be considered and the use of a quantitative calculation approach is compulsory. Then, the ECD spectrum is estimated for each relevant structure and all spectra are averaged. This latter operation also requires the relative populations of the various structures to be known with high accuracy. Spectral averaging is justified by the fact that ECD spectroscopy is a “fast” technique, that is, the observed spectrum is always the superposition of the spectra of all species present. Then the weighted-average spectrum is compared with the experimental one, like in point 4.
6. Finally, if the calculated ECD spectrum or estimated band has the same sign of the experimental one, the assumed absolute configuration is the correct one. Otherwise, it should be reversed.
To the aim of running a conformational analysis, a possible strategy is instead the following.[6]
1. Generate a set of starting structures by means of molecular modeling. They should include only plausible conformations, ruling out those clashing with other evidence coming e.g. from NMR spectroscopy. Additionally, the absolute configuration should possibly be already established. The structural ensemble may be obtained in some cases by systematic variation of one or more dihedral angles, in others by Molecular Dynamics (MD) simulations and related approaches.
2. Calculate a ECD spectrum for each relevant structure.
3. Compare the experimental ECD with the set of calculated ones. If there is a best-matching spectrum, this will be associated with the most probable structure. If not, a single-conformer picture is probably unsuitable and the situation is more complicated.
4. Predictions of ECD spectra
The key point of any ECD analysis is answering the following question: given a certain molecular structure, how can one predict its ECD spectrum, or at least a specific ECD band? Clearly, answering this question means to be able to answer its opposite – and more interesting – one: how can one infer the structure responsible for a certain observed ECD spectrum?
In fact, there is no general answer to this question. Depending on: a) how complex and flexible is the molecular structure; b) which and how many chromophores (if any) does it contain; c) which kind of information – configuration or conformation – is sought; and d) the degree of detail needed, one will need to employ different means or tools to interpret or predict a ECD spectrum. Many of the tools used in the past to interpret ECD spectra are now outdated, for example, the so-called semi-empirical rules like the octant rule for ketones. Modern approaches must necessarily combine practicability and efficiency (or reliability), although the best or most proper compromise between the two has always to be chosen. Three types of approaches will be presented here, in order of complexity: empirical correlations between spectra; the exciton chirality method; quantum-mechanical calculations.
4.1 Empirical correlations
It is quite a common situation that a compound of unknown absolute configuration falls within a family of more or less structurally homogeneous compounds whose configuration is instead known, and that all the family members (including the sample compound) display very similar CD spectra. In such a situation, an empirical correlation may be invoked. Fundamental prerequisites for a safe correlation are: (a) the chromophore(s) responsible for the observed CD spectra are exactly the same; (b) the conformations assumed by the various compounds in the conditions of measurements are comparable.
Let’s consider the example three aryl benzyl sulfoxides 1-3 and their ECD spectra displayed in Figure 4. Let’s also imagine that the absolute configuration of compounds 1 and 2 is known and it is (R) for the samples giving the showed spectra, while that of 3 needs to be established. What would you conclude, based on the mere inspection of the figure? That the enantiomer of 3 giving an almost superposable ECD spectrum to that of the related (R)-1 and (R)-2 should reasonably be (R)-3, too. And such a deduction is correct.
Although much less reliable than many other more modern approaches, empirical correlations between ECD spectra may be very advantageous especially when a large number of similar compounds must be considered. Correlations are however easily prone to errors, and much caution should be paid, usually gained through the experience. Nonetheless, because of the largest practicability and fast response, these methods have survived in years and are still very useful in some situations.
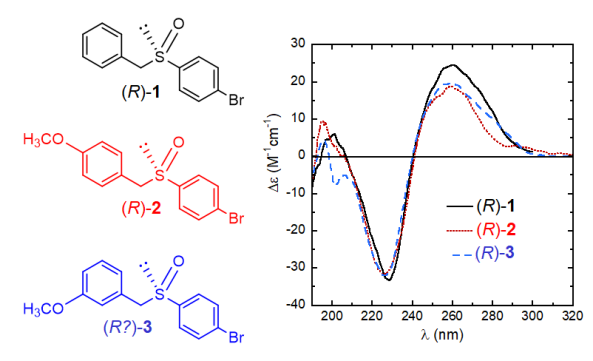
Figure 4. Structures and ECD spectra of sulfoxides (R)-1-3.
4.2 Exciton chirality rule
Exciton chirality[9] occurs when a molecular species (either a covalent one or a supramolecular adduct) contains two or more chromophores, not directly linked to each other (that is, not conjugated), undergoing strong electric-dipole allowed transitions. Usually they include aromatic moieties like those portrayed in the first row of Figure 3. When two or more chromophores come in close contact, thus forming what can be called a multi-chromophoric “aggregate”, their interaction leads to a reciprocal perturbation of their excited states which mix with each other. The extent of mixing depends on the geometry of the aggregate, and if the chromophores are reciprocally skewed, the aggregate is chiral and shows a ECD spectrum. Each electric-dipole allowed transition may be defined through an electric transition dipole moment (the red double arrows in Figure 3). When two such dipoles are not coplanar or collinear (or, more in general, not related by roto-reflection symmetry elements), they can be said to be in a skewed arrangement. In classical terms, the interaction between oscillators may be described as a Coulomb dipole-dipole coupling.
Upon interacting with radiation, the two dipoles start oscillating and they may interact in two ways, namely in-phase or anti-phase with each other. Following classical arguments, the in-phase oscillation has higher energy of the anti-phase one, because of less favorable dipole alignment (head-to-head vs. head-to-tail). In both coupling modes, the overall charge displacement is helical and the two helices have opposite sense of screw, as can be appreciated from Figure 5. These two exciton-coupled transitions occur close in energy (that is, at close wavelemngths) and are associated with rotational strengths of same magnitude and opposite signs. This feature is globally called an exciton couplet.
Both the sign and intensity of a couplet are determined by the reciprocal arrangement of the two dipoles in the space. The sign of a couplet (defined, as the sign of its long-wavelength component) may be inferred in the following way. First, one must look at the molecule from a specific viewpoint: the two dipoles must be viewed along the line passing through their centers. If the dipole in the front can be brought onto that in the back by means of a clock-wise rotation, it is said that they define a positive chirality. The exciton chirality rule states that a positive chirality corresponds to a positive exciton couplet, and vice-versa. Similarly, an anti-clockwise rotation defines a negative chirality corresponding to a negative couplet.[10][11] This is exemplified by the two steroidal bis(p-dimethylaminobenzoate) compounds 4 and 5 (Figure 5). In p-substituted benzoates, the relevant transition (π-π* transition) occurs between 250 and 320 nm and it is polarized parallel to the aromatic “long” axis, i.e., parallel to the alcoholic O–C bond. Therefore the twista angle between the transition dipoles in bis(benzoates) of 1,2-diols is the same of the diol O–C–C–O dihedral angle. The (–) and (+)-gauche arrangement of compounds 4 and 5 is reflected in strong ECCD couplets with, respectively, negative and positive sign.
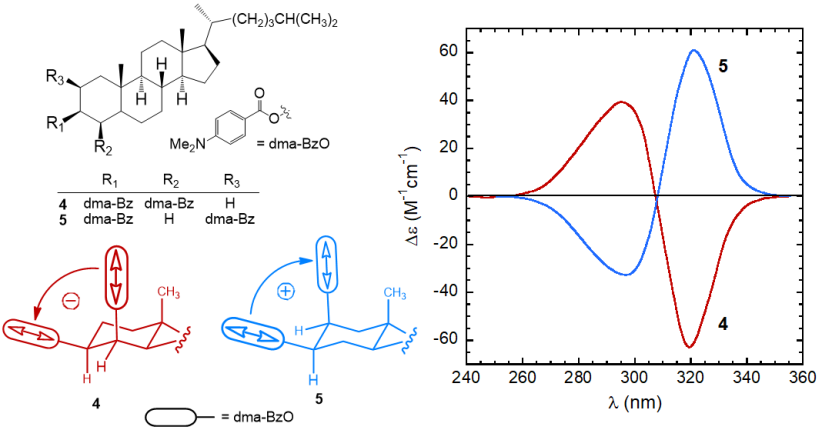
Figure 5. ECD spectra of p-dimethylaminobenzoates 4 and 5 from steroidal 1,2-diols,[8]
and sketch of the molecular portions emphasizing the positive or negative chirality defined by transition dipoles dma-BzO chromophores.
The exciton chirality method for absolute configuration assignments requires the presence of two strong chromophores. In most (but not all) cases, they are purposely introduced in the molecule by chemical derivatization. It is for example the situation of steroidal diols just discussed, where the two hydroxyl moieties were esterified as p-dimethylaminobenzoates. Such a strategy usually involves alcohol, amino and carboxyl groups, and the suitable chromophores include p-substituted benzoate and cinnamate, 2-naphthoate, 2- or 9-anthroate, naphthimide, and so on. The second prerequisite for applying ECCD method is that the exact directions of polarization of the involved transitions are known. This is the case for many well-known chromophores (like those shown in Figure 2), or it may be established by quantum-mechanical calculations or linear dichroism experiments.
4.3 Quantum-mechanical calculations
ECD calculations with quantum-mechanical methods (QM) is nowadays the most frequently employed approach, applicable to moderately large molecules. Any QM method capable of describing excited states (in terms of wavefunctions, transition energies and moments) will provide rotational strengths and thus ECD spectra. In general, chiroptical properties are very sensitive to approximations made in electronic structure calculations. Reliable ECD predictions necessarily require theoretical methods which take electron correlation into account and use of large basis sets, often including diffuse functions. A survey of computational methods may be found in textbooks.[12]
Ab initio methods imply explicit solution of time-dependent Schrödinger or Kohn-Sham equations. Among the several different high-level methods which have been employed for ECD calculations, time-dependent density functional theory (TDDFT) has emerged in the last years as the one leading to the best accuracy/cost compromise.[8] In fact, hybrid DFT functionals like B3LYP, PBE0 and M06-2X predict in many cases transition energies and rotational strengths with high accuracy at a reasonable computational cost. On the other hand, some DFT functional have well-recognized drawbacks, including a poor description of some loosely localized states, such as charge-transfer, diffuse and Rydberg states. These problems may be alleviated using long-range corrected functionals such as CAM-B3LYP and ωB97X-D. Another issue related to TDDFT calculations is that, because of the perturbative nature of approach employed, they are intrinsically more accurate in the prediction of low-lying excited states.
The calculation output is normally a list of rotational strengths Ri at discrete transition frequencies ni, or, in other words, a stick plot. A more immediate comparison with an experimental ECD spectrum requires converting this stick plot in a true spectrum, which means to associate each rotational strength with a Gaussian or Lorentzian shape function (with intensity proportional to the Ri value), and then to sum all bands.[1] The band-widths σi are usually chosen on a nest-fit basis; reasonable values are σ = 1500-3000 cm–1. Expressing the rotational strengths in 10–40 cgs units, the ECD spectrum calculated as sums of Gaussians in the wavenumbers (in cm–1) domain is:
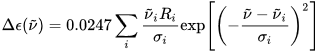
where σi are the exponential half-widths at 1/e height, related to the half-height full widths by 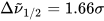 . If computed transition frequencies are systematically shifted with respect to experimental ones, the former ones may be appropriately corrected. To do so, one looks for the best match between computed and experimental UV-vis maxima, and the same shift is applied to ECD spectra (so-called UV correction). After band-shape application and shift correction, the computed spectrum in the wavenumbers domain may be translated into that in the wavelengths domain (
. If computed transition frequencies are systematically shifted with respect to experimental ones, the former ones may be appropriately corrected. To do so, one looks for the best match between computed and experimental UV-vis maxima, and the same shift is applied to ECD spectra (so-called UV correction). After band-shape application and shift correction, the computed spectrum in the wavenumbers domain may be translated into that in the wavelengths domain (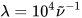 ) normally used to plot experimental spectra.
) normally used to plot experimental spectra.
For a flexible compound, the calculation must be repeated on all conformers populated at room temperature. Thereafter, the various spectra are averaged using the Boltzmann distribution to afford a final calculated spectrum to be compared with the experimental one. An example of calculation for a natuiral product is summarized in Figure 6. The Figure shows: in the left panel, the stick-plot for the lowest-nergy minimum and its conversion into a spectrum; in the middle panel, the averaging procedure over the three populated conformers; in the right panel, the comparison between the weighted-average spectrum and the experimental one.
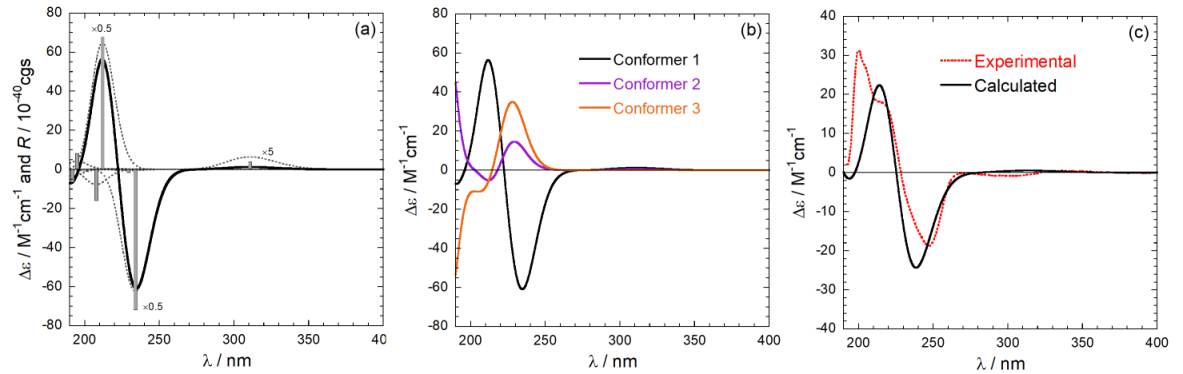
Figure 6. Steps for absolute configuration assignment via ECD calculations. (a) from a stick-plot into a spectrum;
(b) from conformer spactra to a weighted-average spectrum; (c) final comparison.
References
- Günther Snatzke; Circular Dichroism and Absolute Conformation: Application of Qualitative MO Theory to Chiroptical Phenomena. Angewandte Chemie International Edition 1979, 18, 363, 10.1002/anie.197903631.
- ECS technical reports . Ettore Castiglioni’s Legacy. Retrieved 2019-6-3
- Christopher J. Cramer. Essentials Of Computational Chemistry: Theories And Models; Wiley: New York, 2005; pp. 1.
- Daniele Padula; Gennaro Pescitelli; How and How Much Molecular Conformation Affects Electronic Circular Dichroism: The Case of 1,1-Diarylcarbinols. Molecules 2018, 23, 128, 10.3390/molecules23010128.
- Philip J. Stephens; Nobuyuki Harada; ECD cotton effect approximated by the Gaussian curve and other methods. Chirality 2009, 22, 229, 10.1002/chir.20733.
- Nina Berova; Lorenzo Di Bari; Gennaro Pescitelli; Application of electronic circular dichroism in configurational and conformational analysis of organic compounds. Chem. Soc. Rev. 2007, 36, 914, 10.1039/b515476f.
- Gennaro Pescitelli; Lorenzo Di Bari; Nina Berova; Conformational aspects in the studies of organic compounds by electronic circular dichroism. Chem. Soc. Rev. 2011, 40, 4603, 10.1039/c1cs15036g.
- Andrea Mazzanti; Daniele Casarini; Recent trends in conformational analysis. Wiley Interdisciplinary Reviews: Computational Molecular Science 2011, 2, 613, 10.1002/wcms.96.
- Gennaro Pescitelli; Torsten Bruhn; Good Computational Practice in the Assignment of Absolute Configurations by TDDFT Calculations of ECD Spectra. Chirality 2016, 28, 466, 10.1002/chir.22600.
- Nobuyuki Harada; Koji Nakanishi. Circular Dichroic Spectroscopy - Exciton Coupling in Organic Stereochemistry; University Science Books: Mill Valley, 1983; pp. 1.
- Gennaro Pescitelli; ECD exciton chirality method today: a modern tool for determining absolute configurations. Chirality 2021, 34, 333-363, 10.1002/chir.23393.
- Nobuyuki Harada; Koji Nakanishi; Exciton chirality method and its application to configurational and conformational studies of natural products. Accounts of Chemical Research 1972, 5, 257, 10.1021/ar50056a001.




