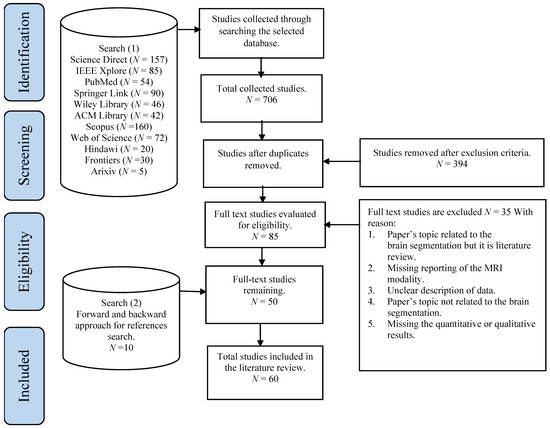
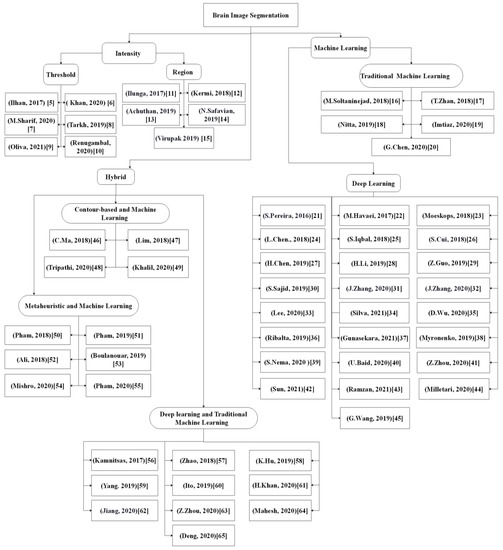
Recently, the deep learning-based method has attracted much research interest due to its excellent performance and ability to automatically capture adaptive features, which outperform manually created features. Moreover, these features were learned in an increasing feature complexity trend, which results in more robust feature learning. During the last few years, more studies have been designed using a combination of the deep learning-based method and the new brain tumor segmentation method. Most of the studies utilized convolutional neural networks due to their effectiveness in detecting patterns in an image, specifically the MR images, with promising results reported. To date, the deep learning-based segmentation was performed using 2D, 2.5D, or 3D MR images, which is elaborated in the following sections.
Deep Learning-Based Methods Using 2D Images
Deep learning using 2D images requires brain image slices or extracted 2D patches from 3D images as an input for the 2D convolutional kernel. Several studies
[21][22][23][24][25][26][27][28][29][30][31][32][33][34][35][36][37] have been published on the deep learning-based method using 2D images. Sergio Pereira et al.
[21] introduced cascade layers using small 3*3 convolutions kernels to reduce overfitting. The study enabled the segmentation of the image into four regions, namely (i) necrosis, (ii) enhancing tumor, (iii) edema, and (iv) normal tissue. Two convolutional neural network (CNN) architectures were trained and used in the proposed work to extract the feature maps, which were low-grade glioma and high-grade glioma. The use of small kernels led to a deeper architecture design, which reduced the number of weights in the network and significantly affected overfitting. However, for the initial phase, the user has to manually identify the glioma grade where prior medical knowledge is required, which is one of the limitations. Additionally, the tissue segmentation was performed as a patch-based task in the study where the local dependency of labels during pixel classification was ignored. Another drawback of the proposed method is the poor segmentation of tumor core regions in the BRATS 2015 Challenge dataset.
Similarly, the application of another novel Cascade CNN model for fully automatic brain tumor segmentation was reported by Havaei et al.
[22]. Cascade architecture of 2D CNN was used in the study to preserve local dependency of labels during pixel classification and extract local and global contextual features which deal with imbalanced tumor labels. However, the model suffers from two drawbacks: (i) poor segmentation between the enhanced and core regions of the brain tumor inferior to the complete tumor and (ii) only the local dependency of the labeled samples was considered, with the appearance and spatial consistency neglected when applied on 3D images.
Moeskops et al.
[23] presented an automatic approach based on a multi-scale CNN for segmenting white matter hyperintensities of presumed vascular origin (WMH) (basal ganglia and thalami, brain stem, cortical grey matter, white matter, cerebellum, WMH, peripheral cerebrospinal fluid, and lateral ventricular cerebrospinal fluid) from MRI modalities (T1, T2, FLAIR, and T1inversion recovery). The proposed multi-scale CNN model was claimed to be the first modern MRI segmentation method that applies CNN for additional WMH segmentation. Furthermore, the model was assessed in two large MRI datasets of older patients that were affected by motion artifacts and varying degrees of brain abnormalities.
Another study by Chen et al.
[24] proposed a 2D novel method based on a CNN architecture identified as Dense-Res-Inception Net (DRINet) for multi-class brain tumor segmentation. The DRINet consisted of three blocks, namely, (i) convolutional, (ii) deconvolutional, and (iii) unpooling blocks. The convolutional block carried out dense connections and was used to alleviate the effect of vanishing gradients. Meanwhile, the deconvolutional block carries out the residual inception modules to aggregate feature maps from different branches. The unpooling block was used for the aggregation of different sampled feature maps. The use of this method resulted in accurate findings on segmenting complex, challenge, multivariate domains (tumor and cerebrospinal fluid (CSF)), and multi-organ segmentation on abdominal CT images. Nevertheless, the DRINet approach has a complex network structure that requires millions of parameters (i.e., billions of connections between neurons and millions of weights), which could lead to a difficult training phase, and testing can be slower depending on the ground truth label requirements.
Iqbal et al.
[25] proposed three different improved network architectures for intra-tumor segmentation, which were an extended version of SegNet (deep convolution encoder-decoder architecture), as follows: (i) Interpolated Network, (ii) SkipNet, and (iii) SE-Net. All three structures consisted of decoder/encoder architecture, and four sub-blocks were used in each phase. A batch of normalization layers was added next to each convolution to avoid the disappearance or explosion of convolutional gradients and to maintain the stability of the training phase. The advantage of this approach includes the use of simple network structures as an intermediate convolutional map along with interpolation methods to produce a quick model with a smaller memory space. However, the method has a limitation where the segmentation performance could be affected if the model is trained with limited ground truth samples.
In the same year, Cui et al.
[26] reported on a hybridized cascade of a deep convolution neural network (DCNN) architecture that can segment 2D brain images automatically in two major steps. Firstly, the tumor region was localized immediately using the pixel-wise fully convolution network (FCN) from the MR images. Then, the patch-wise CNN with smaller kernels and deeper architecture was adopted for further classification of the localized tumor region into multiple sub-regions. This approach alleviates the imbalanced data issue using a hybrid CNN. However, the approach is time-consuming during model training, and inference is required for operating the image patches.
In a different approach, Chen et al.
[27] presented a combination of prior knowledge and a DCNN to enrich the extracted features of DCNN for brain tumor sub-compartment identification. This model requires an analysis of a left-right similarity mask (LRSM) in the constructed feature space and uses LRSM as the location weight of the DCNN features. These features were then used to train the model to determine the asymmetrical location information of the input images via a similarity metric. This approach was found to provide about 3.6% of dice similarity coefficient (DSC) improvement of complete tumor segmentation over the conventional DCNN. The advantage of the proposed method includes the ability to combine the symmetric masks in several layers of DCNN to assign location weight for the extracted features. However, the method could not differentiate between the tumor core regions and the enhanced tumor region as the LRSM mask can reflect a complete tumor situation.
Li et al.
[28] presented an automatic approach based on the improved version of U-Net for multiclass brain tumor segmentation from 2D MR image slices. Firstly, the up-skip connection between the encoding and the decoding elements was proposed to further enhance the information flow and the network connectivity. Then, in each block, an inception module was implemented to assist the network in learning richer representations. Nevertheless, the model suffers from poor segmentation of enhancing tumor region as the whole brain slices were used for model training. This led to a data imbalance issue due to a small number of pixels that belong to enhance tumor and core regions inferior to other brain tissue.
Another approach was reported by Guo et al.
[29], where a supervised multimodal image analysis was performed with three cross-modality of fusion level strategies, which were feature learning, classification, and decision making. The three fusion strategies were implemented and tested in three different patches-based CNNs with corresponding variations in the network structures. Four modalities of imaging (CT, PET, T1, and T2) were used as fused inputs for brain tumor segmentation. Comparison between the single model and multimodality showed that the CNN-based fusion network performed better on PET, CT, and T2 modalities. This approach provides methodological guidelines for designing and applying multimodal image analysis fusion strategies through different implementations of CNN architecture. However, this approach is limited for complete tumor detection. Another limitation is the dramatic decrease in the segmentation performance within the misaligned regions based on the number of affected modalities and severity of the misalignment.
An automated hybrid DCNN model for brain tumor segmentation was presented by Sajid et al.
[30] for different modalities of MR. This model extracted 27 × 27 sized patches from four axial MR modalities to consider both spatial and contextual knowledge for predicting segmentation labels of pixels. The proposed hybrid DCNN model combined the output feature maps of two- and three-CNN paths. The model successfully addressed local dependencies between the output labels, which was the major drawback of the two- and three-CNN paths. By integrating the two- and three-CNN networks, an increase in the effect of neighboring pixels was noted, and the output was recognized based on the local and contextual features. Morphological operations were used to further enhance the segmentation performance by eliminating minor false positives along the edges of the expected outputs. The proposed model segmented the core and enhanced tumor regions better compared to the complete tumor regions. This could be attributed to the fuzzy boundaries of edema that limit the detection of the whole tumor region compared to other regions. However, this approach has a limitation where a large amount of training data and parameters are required for model training.
In addition to the various methods proposed, Zhang et al.
[31] presented a residual U-Net and attention mechanism in a unified architecture named AGResU-Net for patch-wise brain tumor segmentation. Attention gate units were added into the up-skip connection of the U-Net structure to highlight the important feature details along with disambiguates in noise and irrelevant feature responses. The AGResU-Net was found to enhance feature learning by extracting important semantic features focusing on the details of small-scale brain tumor sub-regions, which improves the segmentation performance of the brain tumors. Nevertheless, the AGResU-Net model has a drawback, where an amount of contextual information and local details among different intra-slices were not included due to modeling based on 2D U-Net.
In the same year, Zhang et al.
[32] proposed another new method using attention residual U-Net (AResU-Net) for end-to-end 2D brain tumor segmentation. The AResU-Net embedded a series of attention and residual units among corresponding down-sampling and up-sampling processes. The system simultaneously improved the local responses of down-sampling and the recovery effects of the up-sampling process. However, the model neglects contextual and local details of different intra-slices due to modeling based on 2D slices.
Recently, an innovative brain tissue segmentation method from MR images was proposed by Lee et al.
[33], where a patch-wise U-net architecture was used to divide the MR image slices into non-overlapping patches. Corresponding patches of ground truth were incorporated into the U-net model, and input patches were predicted individually. The model was found to retain the local spatial information better compared to the conventional U-Net model. The design successfully fixed the drawback, specifically the limited memory problem, which was caused by multiple down and upsampling stages. The memory problem was attributed to the storage of parameter values at each stage and difficulty in maintaining local details as the entire image is incorporated into the network. Although the memory problem was resolved using the proposed model, computational complexity was higher in the training phase.
In another study, Silva et al.
[34] proposed a three-stage cascade FCN architecture based on the deep layer aggregation technique to gather further spatial and semantic information for intra-tumor segmentation. The output features of one FCN are directly fed to the next layer for extending the feature hierarchy over different depths for better segmentation refinement. However, the model requires high computational resources and post-processing to refine the extracted tumor regions.
In addition to the various proposed methods, Wu et al.
[35] suggested a multifeatures refinement and aggregation network (termed MRANet) based on CNN for end-to-end brain tumor segmentation. The model fully utilized the hierarchical features by adopting the feature fusion concept at several levels, which extracts low-level, mid-level, and high-level features by sampling similar hierarchical features of encoder and decoder. These features were then aggregated and re-extracted for better segmentation refinement.
Ribalta Lorenzo et al.
[36] proposed a deep learning method for brain tumor delineation from the FLAIR modality of MR using the fully convolution neural network (FCNN) inspired by U-Net. The authors trained the model on 256 × 256 patches extracted from the intra-tumor regions that belong to only positive (tumorous) full-sized FLAIR MR image sequences. Firstly, data augmentation methods were used to expand the dataset and achieve a robust algorithm against the heterogeneity of small training datasets. Subsequently, the FCNN was trained using the DSC to maximize the model training to improve the quality of the segmentation. The proposed FCNN model was claimed to be the best modern FLAIR MR image segmentation method that applied hand-crafted features and was classified using extreme random trees. This model offers controllable training time and instant robust segmentation using the FCNN that was trained on heterogeneous and imbalanced datasets. Nevertheless, this model exhibited potential drawbacks caused by the rapid data augmentation process, as the unnatural increasing number of training patches resulted in a reduction in overall average data accuracy.
Gunasekara et al.
[37] proposed cascaded algorithms for glioma and meningioma brain tumor segmentation and classification. Firstly, CNN was implemented to classify meningioma and glioma regions. Then, the classified images were fed to R-CNN to localize the tumor regions of interest, which was accompanied by active contouring to delineate the exact tumor boundary. Finally, the Chan–Vese level set model was used to segment the target tumor boundary.
Deep Learning-Based Methods Using 3D Images
The second category of deep learning-based tumor segmentation approaches uses 3D MR images for segmentation to overcome the limitation of neglecting contextual information in 2D CNN. Several studies
[38][39][40][41][42][43] have reported the approaches under this sub-class.
The intra-tumor region segmentation method from 3D MR images based on the asymmetric encoder-decoder network was presented by Myronenko
[38]. The researchers adopted CNN’s encoder-decoder structure with an asymmetrical large encoder to extract deep features and reconstruct the dense segmentation masks using a decoder. To tackle the issue of a small training dataset, a variational auto-encoder was added to the endpoint of the encoder, and the input image was reconstructed together with the segmentation to regularize the shared encoder at the inference time. This model enables accurate intra-tumor segmentation based on the unsupervised feature learning method with a lower requirement for ground truth labels and without the post-processing step. However, the proposed method requires high computational resources to accelerate tumor annotation in MR images.
To decrease the dependency on the ground truth images during the training stage, Nema et al.
[39] proposed a RescueNet approach for multi-class brain tumor segmentation utilizing both residual and mirroring principles. Different training was performed to segment whole, core, and enhancing tumors using three different networks. The proposed RescueNet approach was trained based on the unpaired generative adversarial network (GAN) method, which was utilized to enrich data for the training stage with better segmentation results obtained using a larger amount of testing data. Finally, a scale-invariant algorithm was suggested as a post-processing stage to improve the segmentation accuracy. The pros of this approach include robustness to the appearance variations in brain tumors, the minimum requirement of labeled datasets for model training, and that the model is 10% trained and 90% tested. However, this approach requires a post-processing step for further segmentation refinement.
In a more recent study by Baid et al.
[40], an effective weighted patch extraction was combined with a new 3D U-Net architecture for a fully automatic brain tumor segmentation. The authors proposed a weighted patch-based segmentation approach to address the imbalance of class among tumor and non-tumorous patches. The 3D weighted patch-based method and a unique number of feature maps were designed to train the architecture, which enables the accurate segmentation of intra-tumor structures. Finally, a 3D connected component analysis was used as the post-processing method to improve the accuracy of the tumor delineation. However, this approach failed to segment some of the tumor parts with a small necrotic tumor cavity from the MR images due to a large variance in the training and validation dataset features. This can be resolved by increasing the number of training data to overcome the inter-patient variations.
To address the two main challenges, namely, exploding and vanishing gradients affecting the traditional DCNNs performance, Zhou et al.
[41] proposed a novel three-phase framework for automatic brain tumor segmentation of the 3D MR images. Firstly, a dense three-dimensional networking architecture was adopted to construct the features to be re-used. Secondly, 3D atrous convolutional layers were used to design a new feature pyramid module, which was added to the backbone end to fuse the multiscale contexts. Finally, for further training promotion, a supervision 3D deep mechanism was equipped to enhance the network convergence by adding auxiliary classifiers to alleviate the problem of exploding and vanishing gradients by utilizing dense connectivity. Overall, this framework is considered a complete architecture without additional post-processing stages. Furthermore, simple implementation and the use of adjustable parameters are the main advantages of this framework. However, the segmentation of cores and enhancing tumors are inferior compared to the complete tumor, which requires considerable improvement.
In another study, Sun et al.
[42] presented a multipath way 3D FCN architecture for brain tumor segmentation. The model extracts different receptive fields of feature maps from multi-modal MR images using the 3D dilated convolution in each pathway and fuses these features spatially using skip connections. This model helps FCN architectures to better locate the boundaries of tumor regions. However, the model requires a post-processing step, as direct connections between high- and low-level features will lead to unpredictable consequences and the semantic gap between the encoder and decoder.
An effective mapping from MR volumes to voxel-level brain tissue segments was proposed by Ramzan et al.
[43]. A 3D CNN, which utilized the concept of residual learning, skip connections, and dilated convolutions, was applied in the study. Dilated convolutions were utilized to decrease the computational cost by computing spatial features with a high resolution. However, the space complexity of this model was higher as dilated convolution was used, and down-sampling of input volumes was neglected, which led to an increase in the number of parameters and kernels by a certain factor.
Deep Learning-Based Methods Using 2.5D Images
Although 3D deep neural network (DNN)-based segmentation can better exploit 3D features of 3D MR image information data, this approach has limitations related to network intensiveness and memory consumption. Therefore, another category of 2.5D DNN was researched. In comparison to the 2D and 3D DNN, 2.5 DNN has inter-slice characteristics and lower memory demand.
An automated 2.5D patch-wise Hough-CNN model based on a voting strategy for localizing and segmenting brain anatomies of interest (26 regions of the basal ganglia and the midbrain) was presented by F. Milletari et al.
[44] for different modalities of MRI and ultrasound slices. The patch-based voting strategy was designed and integrated into the Hough-CNN model to localize and segment brain structures that are corrupted by artifacts or are partially visible.
To overcome network complexity and memory consumption of the 3D based-segmentation methods, Wang et al.
[45] suggested a cascade of 2.5D CNN voxel-wise architecture for sequential segmentation of brain tumors from MR images. The task of multiclass segmentation was largely divided into a sequence of binary hierarchical tasks to segment complete, core, and enhancing tumors for better utilization of hierarchical features of brain tumor structures. The resultant segments were then used as a crisp mask to identify tumor cores and enhancing tumors, which could lead to anatomical constraints during the final segmentation. The predicted tumor core was constrained to be within the whole tumor, while the enhancing tumor region was within the core tumor region. Additionally, the test-time augmentation technique was used to obtain structure-wise and voxel-wise uncertainty estimation of the segmentation results. Finally, a CRF was proposed as the post-processing stage to smoothen the segmentation results. A robust segmentation resulted in a balanced property of memory consumption, model complexity, and multi-view fusion. However, the method has two main limitations: (i) it is highly dependent on the voxel-wise annotations technique and (ii) time-consuming for large datasets. Additionally, this approach requires post-processing for segmentation tuning. The advantages and disadvantages of all of the discussed segmentation approaches are summarized in
Table 1.
Table 1. Strengths and limitations of intensity-based and machine learning approaches for brain segmentation.
| Categories |
Ref |
Strengths |
Limitations |
| Thresholding |
[5][6][7][8][9][10] |
-
Simple implementation.
-
Low computation time.
|
|
| Region based |
[11][12][13][14][15] |
-
High segmentation accuracy required for tumor regions.
-
Low computation time.
-
High segmentation efficiency for 3D images.
-
High segmentation performance in complex regions.
|
|
Traditional
machine learning |
[16][17][18][19][20] |
|
-
Parameter initialization is subjective.
-
Requires skillful users.
-
Low segmentation performance for semantic type segmentation.
-
Optimum representation features determination is very subjective.
-
Model trapped in a local minimum due to imbalance between exploration and exploitation.
|
| Deep learning |
[21][22][23][24][25][26][27][28][29][30][31][32][33][34][35][36][37][38][39][40][41][42][43][44][45] |
-
Adaptive feature map.
-
High performance of semantic-based segmentation.
-
High performance in complex regions.
-
Best segmentation results compared to other categories.
|
|