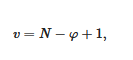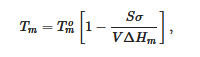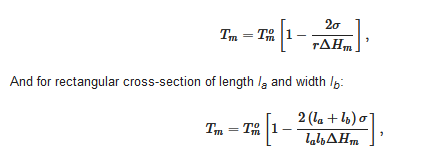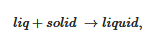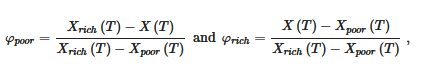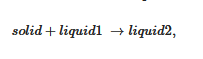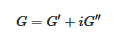The physics side of organogelation is broached through three main aspects, thermodynamics (formation and melting), structure (morphology and molecular organization), and rheology. Organogelation is a system constituted of fibril-like entities. Gel formation occurs through first-order transitions, chiefly by homogeneous nucleation.
1. Introduction
The purpose of a definition is to specify the extension of a concept, namely, here, organogelation, and to identify the objects belonging to a specific set, namely, objects possessing common characteristics and/or properties. Most books and papers attempting to define a gel quote the famous sentence by Dorothy Jordan Lloyd: “The colloidal condition, the gel, is one which is easier to recognize than to define” [1]. This question has been largely tackled in the case of polymer thermoreversible gels with always the same ambiguous answers [2][3][4][5]. To be sure, a gel is capable of “jailing” a large amount of solvent, the latter being by far the major component, which is probably the only unquestionable statement. In principle, a gel is supposed to behave as a solid material that possesses an elastic modulus at zero frequency in oscillatory measurements or at infinite time in relaxation experiments.
Guenet has suggested replacing the rheological definition, which is too restrictive, by contemplating two criteria that involve the topology of the gel and its thermodynamic property [6][5]. As commonly accepted, a gel is basically a network, whose definition as given in any language dictionary is: “a large system of lines, tubes, wires, etc. that cross one another or are connected with one another”. This lays the ground for the topological criterion. As these gels are thermoreversible, namely, they melt on heating and reform on cooling for unlimited cycles, the thermodynamic criterion states that the gel formation/melting process must occur through first order transition. These two criteria define a set of objects that can be designated as fibrillar organogels [6][5].
Figure 1 shows two examples of organogels complying with the first criterion as they are made up with fibrils connected randomly (randomly-dispersed network) or connecting at a center (hub-like network)
[7][8]. As will be shown below, these gels do form and melt through first order transitions. We shall see in the section devoted to rheology that some fibrilllar organogels obey the rheological definition, some obey it partially, and some do not at all. The fibrillary nature has generally an impact upon the visual aspect: a gel is usually slightly translucent, even transparent in some cases, with a blueish tinge due to blue light being more scattered than the other radiations (see 15 for details). Usually, when a system displays strong turbidity its gel status is rarely confirmed.
Figure 1. (a) TEM micrograph of an OPVR/trans-decahydronaphthalene, which shows a typical randomly-dispersed network (b) optical micrograph of an OPVOH/trans-decahydronaphthalene organogel displaying a hub-like network where fibrils radiate from and connect to nodes (arrows).
2. Thermodynamics
2.1. Fibrils Growth
It should be realized that organogelation is chiefly a crystallization process as we shall discuss in more detail below. This is therefore a
nucleation-controlled phenomenon
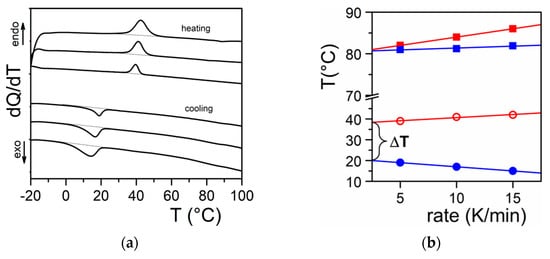
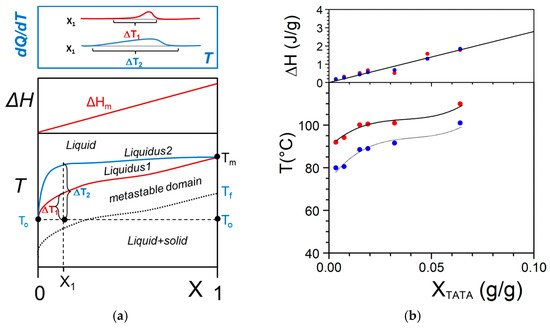
[9][10][11]. DSC experiments do highlight this process through the observation of formation exotherms and melting endotherms (
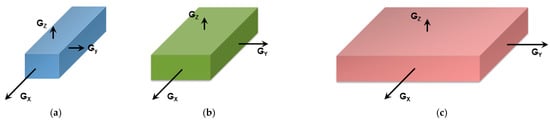
Figure 2a). That fibrillar structures are obtained arises simply from the faster growth of one crystal face with respect to the other two as highlighted in
Figure 3. Here, for fibrils to grow one has G
x >> G
y and G
x >> G
z (
Figure 3a). If G
x >> G
z with G
x > G
y (
Figure 3b) one may expect the formation of lathes. Finally, if G
x ≈ G
y >> G
z (
Figure 3c), then platelets and correspondingly spherulites are obtained. The resulting spherulitic morphology does not comply with the topological criterion discussed above.
Figure 2. (a) DSC thermograms obtained on heating (endo) and on cooling (exo). Scanning rates 5, 10, and 15 °C/min; (b) variation of the melting peak peak (◯) and the formation peak (●) for Tri-aryl-triamine/tetrachloroethane organogel (C = 0.02 g/g). (■) and (■) stand for pure naphthalene for the sake of comparison.
Figure 3. (a) fibrillary shape due to the fact that the growth rate along the x-direction, Gx, is much faster than those in the other two directions (Gx >> Gy and Gx >> Gz). (b) formation of a lath when Gx > Gy >> Gz; (c) when Gx = Gy >> Gz, then formation of extended platelets is expected.
A typical example is given by oligo phenylene vinylene molecules (OPV) studied by Ajayaghosh and coworkers
[12]. One growth face involves π-stacking, the second one H-bonding, and the third one van der Waals interactions. In this system the fastest growth occurs through the π-π interactions. The
chimera character of the organogelators has another probable consequence on the onset of the gelation process. As highlighted in
Figure 2b one usually observes a large undercooling Δ
T between the formation temperature and the melting temperature.
2.2. Phase Diagrams
The mapping out of the temperature-composition phase diagram is an important step in the study of organogels. It should be carried out first as it delivers essential pieces of information for the determination of the structure, and properties of the gels.
These temperature-composition phase diagrams are constructed by applying the two fundamental Gibbs’phase rules
[13][14][15]:
- the variance of the system v, which stands for the number of variables that can be changed without altering the state of the systems. When only the temperature is varied (all other external stimuli being kept constant), the variance reads:
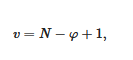
where N is the number of components and φ the number of phases. For two components, the number of phases cannot exceed φ = 3 as the variance is v = 0 under these conditions. This implies that the co-existence of the three phases is restricted to a point. The notion of variance possesses another key outcome, the occurrence of non-variant thermal events, namely, the transition temperature remains constant in large range of composition. Note that the composition is always given in w/w or mol/mol so that it does not depend upon temperature, while the concentration expressed in g/cm3 does.
It is worth emphasizing that only the melting temperature is a thermodynamic characteristic unlike the formation temperature, as the latter is nucleation-controlled, and therefore depends upon external factors. Yet, the melting temperature depends upon the size of the crystals. The Gibbs-Thomson equation (actually first derived by Rie) [16] relates the melting temperature Tm of finite-sized crystals to that of infinitely-large crystals Tom through:
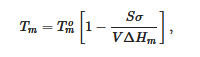
where V is the crystal’s volume, σ and ΔHm the same as in relation 1. For cylinders of cross-section r, relation 6 reduces to
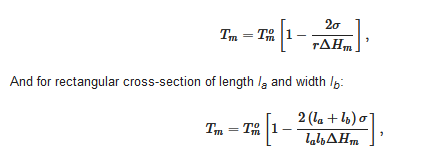
In most cases, cross-sections are large enough so that the effect is rather limited, or even undetectable as far as the melting temperature is concerned. Yet, this is something to keep in mind when processing the DSC data; the more so as fibrils cross-sections depend on the depth of the quench (see section devoted to molecular structure).
2.2.1. Solid–liquid transformation
The simplest case is shown in Figure 4a where the melting temperature of the gel, defined as the liquidus line, increases monotonously with the gelator composition. On cooling two phases form: the gelator-poor phase (the dilute phase), and the gelator-rich phase (the gel). At the liquidus line the following transformation occurs:
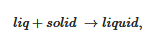
Figure 4. (
a) The simplest T-X phase diagram for a two-component system. Two liquidus lines are considered with two different Δ
T at a given [
X1,
To] coordinate. The dotted black line stands for the gel formation.
Tm and
Tf are the melting and the formation temperatures of the pure gelator. Top, Tamman’s diagram. Above: shape of the expected endotherms; (
b) experimental T-C phase diagram for Tri-aryl triamine/bromobenzene organogels (
[17][18]; (
●) = melting, (
●) = formation. Note the low composition range for the gelator.
The proportion of the different phases is given by the lever rule. For example the fraction φ of the different phases read at a temperature T:
where X(T), Xpoor(T) and Xrich(T) are the compositions of the solution, the poor phase and the rich phase, respectively, at a temperature T. For example sample standing at T = To for X1 one has Xpoor(To) ≈ 0 and Xrich(To) = 1, and therefore φpoor = 1− X1 and φrich = X1.
2.2.2. Liquid–Liquid phase separation prior to gelation
As aforementioned, more complex systems may occur. The case of a liquid–liquid phase separation process that interferes with gelation has already been observed [19]. A typical phase diagram is shown in Figure 5a. The binodal line defines the miscibility gap where two liquids coexist. This type of transformation is designated as a monotectic transition. At the monotectic point XM, one obtains the following transformation:
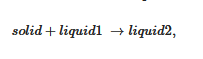
Figure 5. (
a) A T-C phase where a monotectic transformation is observed. At the monotectic point the solid transforms into two liquids of differing compositions. The red lines show the shapes endotherms expected by DSC. The variations of the enthalpies associated with the different transitions are shown above. (
b) Experimental example observed with BHPB-10 in
trans-decahydronaphthalene, X
BHPB is in gram of organogelator per gram of gel. The red arrows stand for optical microscopy investigations, solid symbols = formation and melting of the gel, open symbols = liquid–liquid phase separation; blue arrows stand for the DSC data. Arrow orientation indicates cooling (down) or heating experiments (up); The slight discrepancy between DSC temperatures and optical microscopy findings arises from the use of different cooling and heating rates (5 °C/min and 0.5 °C/min); above Tamman’s diagram
[19].
By cooling within the miscibility gap (dotted line in Figure 5a) the solution decomposes first into two liquids prior to crystallizing. Crystallization eventually occurs as soon as the monotectic line is crossed. As a result, the outcome, and correspondingly the gel morphology, can differ whether the system consists of solution prepared below or above the monotectic composition XM. Below XM the final gel morphology is decided by the first-occurring liquid–liquid phase separation (except for a small region at very dilute compositions). Above XM, a simple crystallization occurs which is followed by a change in liquid composition below TM. Here, the use of relations 3 and 4 is totally irrelevant as the gel melting remains constant in a large range of composition.
The system BHPB-10 in
trans-decahydronaphthalene illustrates this type of situation (
Figure 5b) where one observes a miscibility gap together with a non-variant event. There also exists a significant metastable domain revealed both by DSC and optical microscopy
[19].
The occurrence of a liquid–liquid phase separation is backed up by optical microscopy where droplets are seen prior to gelation (Figure 6a). Then, gelation takes over by forming snake-like structures that connect the droplets (Figure 6b). The aspect of the gel depends considerably upon the cooling rate for X < XM. Cooling slowly allows the growth of droplets before gelation sets in. Conversely, a rapid cooling allows the system to cross the monotectic line before decomposition into two liquid phases can take place. Under these conditions, no special features can be observed in optical microscopy (Figure 6). It will be seen in the next section that the gel morphology is totally different. Yet, the way the gel is prepared, slow cooling or rapid quench, has no effect on the melting properties as ascertained by DSC.
Figure 6. Optical micrographs obtained on BHPB-10/
trans-decahydronaphthalene systems X = 0.05 g/cm
3 (
a) within the miscibility gap; (
b) just after crossing the monotectic line
[19].
2.2.3. Molecular compounds organogelator/solvent
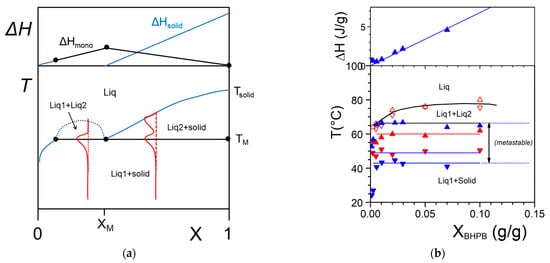
The occurrence of molecular compounds that form between the organogelator and the solvent has already been reported in several papers
[8][20][21]. To the best of the author’s knowledge no extensive phase diagrams have been mapped out for these systems. Theoretical examples of what would be expected with these systems are displayed in
Figure 7.
Figure 7. T-C phase diagrams. The red lines show the corresponding DSC traces. The Tamman’s diagram for the enthalpies associated with the different thermal events is shown on top. (a) for a molecular compound formed at X = Xc. The complex further forms an eutectic compound at X = Xeut. (b) an incongruently-melting compound where the molecular compound decomposes into a liquid phase and a solid phase at its stoichiometric composition.
2.2.4. Metatectic tranformation
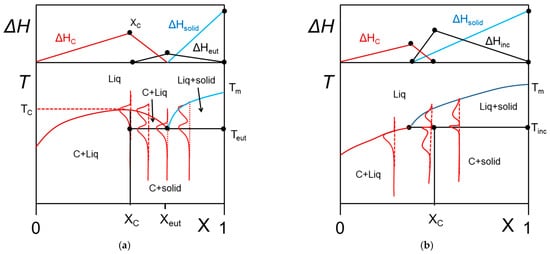
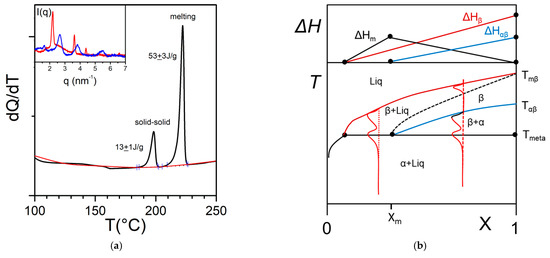
In some cases, the organogelator can exhibit two crystalline forms in the solid state, and a α form that transforms into a β form at Tαβ (solid-solid transformation Figure 8a). At the metatectic point one obtains:
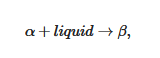
Figure 8. (a) The metatectic transformation can exist if there exists two crystalline forms, α form and β form of the gelator in the solid phase (here a tri-aryl tri-amine, TATA). At Tαβ = 198 °C the α form transforms into the β form as evidenced by the change of diffraction pattern in the inset: blue line at T = 20 °C, red line at T = 200 °C. (b) T-C phase diagrams for a metatectic transformation. The red lines show the corresponding DSC traces. The Tamman’s diagram for the enthalpies associated with the different thermal events is shown on top.
3. Morphology, Molecular Structure
As stated in the definition section, organogels are made up with an array of fibrillar elements whose mesh size lies in the micrometre range. The gel fibrils display in most cases circular cross-sections (Figure 9a,c), or ribbon-like, rectangular cross-sections (Figure 9b,d). These cross-sections have sizes typically ranging from 100 to 1000 nm.
Figure 9. (
a) AFM micrograph of BHPB-10/
trans-decahydronaphthalene. Nanotubes arise from the twisting and fusion of lamellae (
b) AFM micrograph of BHPB-10/cis-decahydronaphthalene. (
c) SEM micrograph of BHPB-10/
o-xylene gels, arrows indicate domains where fibrils twist around one another. (
d) TEM micrograph of OPVR/
trans-decahydronaphthalene gels. (
e) SEM Propargyl Ammonium-Based molecule/H
2O SEM TATA/bromobenzene gels.
[7][8][22][23].
The morphology depends also upon the solvent type as illustrated by Figure 9a–c. In the case of BHPB-10 the nature of the solvent conformer, trans or cis-decahydronaphthalene produces different morphologies: nanotubes for the former against lamella for the latter. Similarly, nanotubes of Figure 9c are no longer produced with aromatic solvents.
The pictures shown in Figure 9a,c highlight that fibrils can be connected to one another, through parallel aggregation (Figure 9a), and/or by twisting around one another (Figure 9c), generating in both cases super-fibrils. Connections in ribbon-like structures are generated both by fibril splitting together with parallel aggregation something reminiscent of a railway system (Figure 9d). In other systems, that can be designated as an array of lathes (Figure 9e), a very limited number of connections are established, somehow resembling a Mikado game. Finally, in some systems display a jumble of fibrils (Figure 9f). It goes without saying that the degree of connectedness has a direct bearing upon the rheological properties as will be reviewed below.
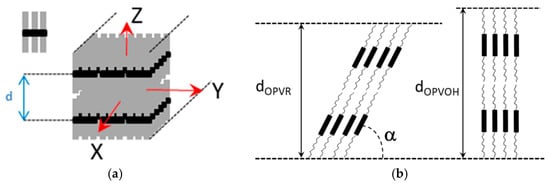
Here, it is worth emphasizing that a small alteration of the organogelator chemical structure has a dramatic effect on the crystal organization as is illustrated by gels from OPVOH and OPVR in benzyl alcohol (
Figure 10). These organogelators only differ in their terminal groups, yet, only one very narrow peak is seen for OPVOH against three peaks for OPVR. This means that the highest order for OPVOH occurs along the z-direction (see
Figure 11a), namely, along the 001 crystallographic plane, although the fastest growth rate is along the X-direction, namely, along the 100. Also, Dasgupta et al. have suspected that the benzyl alcohol may interact with the OH group of the OPVOH so as to form a molecular compound along the Y-direction. This may prevent from a long-distance organization in this direction, hence the absence of a 010 crystallographic peak
[7]. In addition, the distances between the layer lines determined from electron microscopy diffraction as well as from the SAXS patterns imply that the piling in the X-direction is different. Unlike the OPVOH the OPVR molecules are tilted by an angle α = 41° ± 5° (
Figure 11b)
[7]. For OPVR the first three peaks are therefore the 001, 010, and 002.
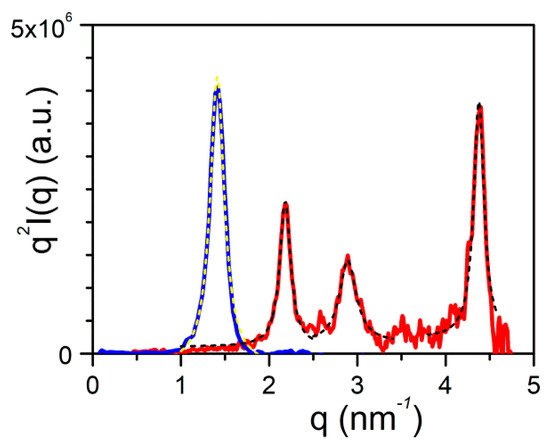
Figure 10. SAXS scattering: blue line is the diffraction patterns for OPVOH, and red line for OPVR gels in benzyl alcohol
[7]. Dashed lines stand for the fits of the different peaks with Equation (16).
Figure 11. (
a) Sketch of an OPV fibril, the molecule is shown as a black core with grey aliphatic arms. X is the growth direction (
b) sketch of the crystal organization seen sideways along the Y-direction. Unlike the OPVOH molecules the OPVR molecules are tilted by an angle α = 41° ± 5°. This gives a core-to-core distance of d = 0.5 nm against d = 0.35 nm for the π-π packing in OPVOH
[7].
4. Rheology
The determination of the rheological properties is an essential aspect in the investigations of gels. The goal is to find out whether one is dealing with an ideal gel and/or how far the gel departs from ideality. An ideal network is supposed to possess an elastic modulus E, namely, a direct relation between the applied stress and the deformation σ = Exε, which remains constant either at constant deformation and/or constant stress. Yet, a gel is a special network in that it contains a very large fraction of liquid. As a result, there is always a viscous effect due to the internal frictional force that takes place between adjacent layers of fluid. A gel is therefore best characterized by a complex modulus:
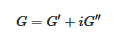
where G’ is the elastic term (storage modulus) and G″ the viscous term (loss modulus). It is usually admitted that a gel of the type organogel [6][24] and/or polymer thermoreversible gel [2][5] can be considered ideal when G′ >> G″ within the explored frequency range in oscillatory experiments (Figure 12). Another parameter is the angle δ, which measures the dephasing between G’ and G” (tan δ = G”/G’). For a purely elastic system δ = 0°, while for a purely viscous system δ = 90°.
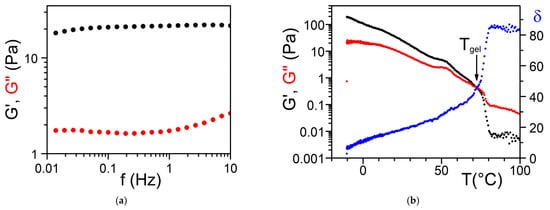
Figure 12. Tri-aryl triamine gels in bromobenzene; (
a) Variation of
G’ and
G” as a function of frequency at T = 20 °C. (
b) Variation of
G’,
G” and
δ as a function of temperature for a frequency of 1 Hz
[18].
5. Conclusions
Sticking to the definition developed above, namely, a gel must consist of highly elongated, crystalline objects, implies to design systems that are to display a crystallization behaviour that privileges crystal growth in one direction. As suggested by Guenet the candidates must be “
chimeras” molecules, that is to be an assembly of parts with differing interaction properties such as hydrogen bonding, Van der Waals interaction or/and π-π interaction. The presence of long aliphatic arms is often a prerequisite
[6]. The OPVOH molecules synthesized by Ajayaghosh and coworkers stand as a paradigm in this respect
[12].
The above conditions automatically entails that these potentially gelling molecules possess rather large molecular weights. They are often designated as low-molecular weight gelator (LMWG) as these gelators usually possess molecular weight larger than usual organic molecules, such as solvents, but much smaller molecular weights than macromolecules. Yet the term “low-molecular-weight “is confusing, after all solvents are also low-molecular weight molecules! It is felt that the term “mesomolecules” might be more appropriate for naming these types of molecules.
These prerequisites are chiefly indicative as the gelation behavior can be totally different in a series of molecules. For instance, the capability of BHPB molecules to produce nanotubes depends strongly upon the length of the aliphatic arms
[25], which makes uncertain prediction of its gelling property. Other major factors to be considered are the path followed when cooling the solution, especially when a miscibility gap exists, the solvent type, and the like. For instance, BHPB forms nanotubes in aliphatic solvents but not in aryl solvents
[26], which suggests the possible existence of molecular compounds
[6].