1. NRVS Transitions and Selection Rules
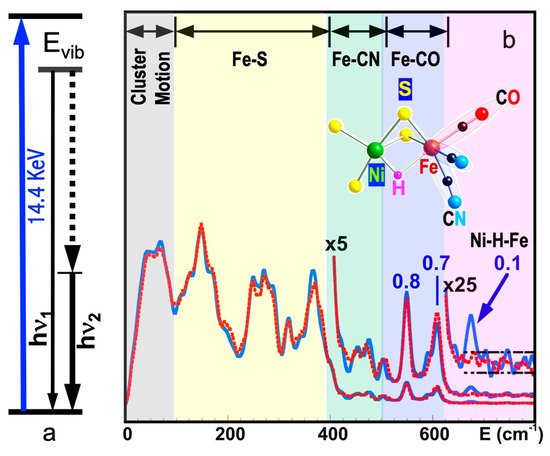
Figure 1a shows the basic principle of NRVS transitions; while an incident X-ray beam scans through an interested energy region to cover the nuclear transition and the associated vibrations (e.g., E1 ~ 14.41425 keV for 57Fe), the nuclear back radiation can be monitored as the scattering energy (E2 = hν1). The total intensities collected from both the direct nuclear fluorescence at hν1 and the internally converted electron K shell fluorescence at hν2 vs. the vibrational energy Evib = (E1–E2) is a raw NRVS spectrum. In this sense, it is similar to resonant optical Raman spectroscopy where vibrational information is extracted in an inelastic scattering from laser light excitation. An NRVS spectrum includes Stokes (creation of phonons) and anti-Stokes (annihilation of phonons) branches, although Figure 1a only illustrates the Stokes transitions. It is also similar to Mössbauer spectroscopy (MS), except that MS measures the recoilless hyperfine interactions, while NRVS measures the recoiled transitions due to vibrations. The raw NRVS spectra can be transformed to partial vibrational density of state (PVDOS), which is independent of any experimental conditions and is calculable via theory-based mathematical simulations. Figure 1b provides an example of such PVDOS.
Figure 1. (a) An illustration of NRVS transitions; (b) 57Fe NRVS spectra for DvMF NiFe hydrogenase (reaction center structure = insert) in a hydride (blue) and deuterated sample (red). The peak assignments (bold black text) and peak counts per second (the blue numbers) are given for the hydride sample (blue curves).
One of the central relations for any spectroscopy is the algebraic selection rule(s), which tell where the allowed transitions occur and, thus, what the spectral profile is like. For NRVS, there are major factors that govern its intensity distribution
[1]. Since this article focuses on the experimental science, we omit the details of the formula deduction but summarize the conclusions instead.
As for any spectroscopy, the intensity for NRVS is proportional to the sample’s concentration and the population distributed on the ground state (e.g., the ground vibrational level). The ground-state population distribution is also a function of the ambient temperature T of the statistical ensemble.
Similar to other inelastic scattering process, NRVS also has a general ∝ 1/Evib dependence that reduces its signal for higher-energy transitions.
Similar to Mössbauer transition, the NRVS signal level is proportional to the Lamb–Mössbauer factor (f
LM or LM factor for short). The LM factor (f
LM) signifies the probability, i.e., whether or how likely a nuclear resonance will take place. For example, free atoms or gaseous samples have almost zero LM factors and have no nuclear resonance, neither Mössbauer nor NRVS. Isotope type and sample temperature T are also the factors that affect the LM factor.
57Fe is one of the few isotopes that show a significant nuclear effect even at room temperature (RT), while the nuclear transition for most other isotopes can only be observed at a cryogenic temperature. This poses a fundamental problem for
operando investigations of materials, which function only at ambient or high temperatures. In addition, the LM factors depend on the molecular environment of the probed nuclei. For example, the iron in lithium iron phosphate undergoes changes in the oxidation state during de-lithiation, and so does its LM factor, which Aldon et al. have demonstrated recently
[2].
If one assumes a harmonic vibrator inside a lattice or a molecule, then the whole transition
S(
E) can be separated into the nuclear resonant transition
δΓ(
E), the single-phonon transition
S1(
E), and multiple-phonon transitions
Sn(
E) as in Equation (1).
For large fLM (such as fLM(57Fe) = 0.8 at low temperature), the S1(E) will dominate the NRVS transitions: NRVS ~ S1(E).
The single-phonon transition or fundamental vibration
S1(
E) which we care the most for is proportional to the ‘mode composition factor’,
e2jα, as expressed in Equation (2):
where
r2jα is the mean square displacement and describes the displacement for a particular atom
j in a particular vibrational normal mode α. Thus, the
NRVS for a particular vibrational mode α is proportional to the mean square displacement of the isotope
j in the nuclear transition (e.g.,
j =
57Fe), as illustrated in Equation (2). This defines the selection rule for NRVS, similar to the transition dipole moment in IR spectroscopy or the polarizability tensor in Raman spectroscopy. The formula also sets the foundation for a calculable PVDOS
[3][1][4][5].
Although most NRVS experiments are conducted on powder samples or frozen solutions with random molecular orientations, there is additional anisotropy information, which can be gained when single crystal samples are examined. This may sound interesting for the condensed matter physics community, but every discipline interested in vibration properties should be interested in anisotropy of their systems. For example, NRVS will be different for an incident beam along three perpendicular directions in the sample (x, y, and z); for this case, there will then be three distinct mode composition factors, e2jα,x, e2jα,y, and e2jα,z, corresponding to the projection of the nuclear motion along x-, y-, and z-axes.
2. Historic Evolution of NRVS
As a nuclear scattering spectroscopy method, NRVS is related to traditional Mössbauer spectroscopy. In 1958, prior to his doctoral exam, Rudolf Mössbauer was the first to discover the recoilless nuclear resonant absorption (the Mössbauer effect) on
191Ir
[6][7], followed by that on
187Re,
177Hf, and
166Er. Since then, the effect has been found in about 40 elements, 90 isotopes, and 110 nuclear transitions, with
57Fe at 14.4125 keV being one of the most useful and most researched transitions. Probing vibrations and dynamics through coupled nuclear transitions was also proposed almost immediately after the discovery of Mössbauer effect and explored in the early 1960s
[8][9]. For laboratory-based Mössbauer spectroscopy, incident energies are tuned via Doppler effect by moving a radioactive source back and forth. Without difficulty, it is possible to provide an energy span for Mössbauer spectroscopy, which has a less than 100 neV in its energy span. However, in order to measure vibrations, an energy span of about 100 meV (or even 200 meV) is needed, corresponding to a speed to move the radioactive source at about 2 km/s (for
57Fe), six orders of magnitude faster than a typical Mössbauer experiment. Therefore, such a setup (for NRVS) is considered mechanically difficult and dangerous, as well as impractical. In short, an entirely different type of X-ray source is required for a NRVS experiment.
Synchrotron radiation (SR) is the electromagnetic radiation emitted by electrons when they travel along a curved trajectory at relativistic speeds (close to the speed of light where relativistic corrections determine the physics). SR at highly advanced facilities has many advanced properties including a high beam flux, a wide/adjustable energy range, a small beam size and a good beam collimation
[10][11]. Using SR as a light source for nuclear resonance spectroscopies was proposed in 1974
[12] and first explored in the mid-1980s with a successful nuclear Bragg diffraction (a nuclear elastic scattering) in yttrium iron garnet material
[13]. For comparison, a regular Bragg diffraction (very important in X-ray crystallography) is elastic electronic scattering. For this pioneering experiment, a nuclear Bragg monochromator was developed which contained two 15 µm thick single crystal films from an yttrium iron garnet (we believe this was Y
3Fe
2[FeO
4]
3) epitaxial grown on a gadolinium gallium garnet (we believe this was Gd
3Ga
5O
12) substrate with 30 mm diameter. The iron garnet films were enriched to 88% with
57Fe
[13]. In the mid-1990s, with most of the proposed fundamental issues explored and a few third-generation high-energy SR rings available, scientists at three SR centers near-simultaneously made successful observations of the recoiled nuclear inelastic scattering caused by vibrational dynamics
[14][3][15]. These SR centers are the three current super SR centers on the globe, SPring-8, APS, and ESRF, which remain the major global hubs for nuclear resonance spectroscopies up to today.
After the initial observations, on the basis of the high-brightness third-generation SR and the continuous improvement of tunable monochromators with sub-meV resolution, use of NRVS has boomed.
57Fe NRVS, as well as various nuclear resonant scattering (NRS) spectroscopies, has attracted particular attention among physicists and geophysicists first because iron is an archetypal transition element and is a dominant component in the cores of the Earth and other terrestrial planets. Since 2001,
57Fe NRVS has enjoyed particular emphasis in inorganic biochemistry research, on various metalloenzymes such as myoglobin and heme systems
[16][17][18], [NiFe] hydrogenase
[19][20][21], [FeFe] hydrogenase
[22][23], other hydrogenases
[24], Mo-nitrogenases
[25][26], nonheme systems
[27], and various iron–sulfur systems
[20][28][29][30]. Meanwhile,
57Fe NRVS application to other research fields, as well as NRS/NRVS for isotopes other than
57Fe, has also been evaluated and published
[31][32][33].
3. NRVS Advantages
Advantages of a synchrotron-based Mössbauer method are the small beam size and very good beam collimation. This allows for many applications in chemistry, biology, materials science, geosciences, high-pressure physics, and many more, particularly because conventional nuclear methods require large amounts of sample, the provision of which can be a costly endeavor or even a technically impossible undertaking. Polarization of synchrotron radiation also allows for studying the magnetic structure of the specimen
[34].
The most prominent advantages of NRVS include but are not limited to being able to extract site-specific information from highly complex systems (e.g., from biological molecules
[35][25][19][36][20][37]), having an almost zero background
[19][36], and having a theoretically calculable PVDOS
[3][35][5][18].
Using
57Fe NRVS as an example, the NRVS selection rule (Equation (2)) excludes all the non-
57Fe vibrations. For example, an [FeFe] hydrogenase enzyme such as the one in
Figure 2a1 often has various iron–sulfur clusters in addition to its H-cluster (a2) which hosts the reaction center [2Fe]
H (a2, green circled and shaded)
[22][38]. Nevertheless, we are now able to identify and label the two irons just inside the [2Fe]
H center or six irons inside the H-cluster with
57Fe while leaving other irons unlabeled
[22][23][39][40]. This lets the corresponding NRVS spectra specifically represent the irons inside the [2Fe]
H center (or H-cluster). NRVS is, therefore, a perfect tool to pinpoint the site-specific information inside a complicated molecule, such as the various enzymes including hydrogenases and nitrogenases
[41][42].
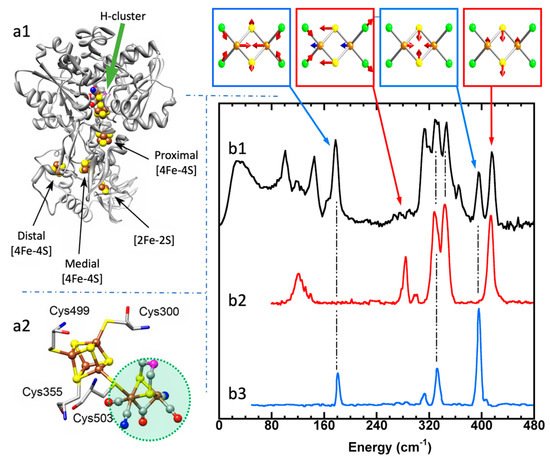
Figure 2. Left panel: structure for an [FeFe] hydrogenase (a1) and its reaction center (H-cluster, six irons) (a2). The green shaded area in (a2) is the reaction center [2Fe]H subcluster (two irons). Right panel: NRVS-derived PVDOS (b1, black) along with IR (b2, red) and Raman spectra (b3, blue) for [Fe2S2Cl4]=. The top inserts above (b1) illustrate a few distinct vibrational modes for this complex.
On the other hand, NRVS also has the ability to show almost all the
57Fe-related vibrations provided these vibrational modes have
57Fe in motion.
Figure 2b is the NRVS-derived PVDOS (b1) along with IR and Raman spectra (b2, b3) for a complex ion [Fe
2S
2Cl
4]
= [43]. In its total 18 vibrational modes, 16 of them have NRVS signals, leading to a rich PVDOS as shown in (b1). The top inserts illustrate a few distinct vibrational modes for this complex; all of them have NRVS signals while three of them have prominent NRVS peaks. In comparison, IR (b2, red) or Raman (b3, blue) spectra for this complex each only has a few transitions (peaks).
Due to the simplicity of the NRVS intensity distribution (Equation (2)), the pure molecule-based experiment-independent PVDOS can be obtained from the raw NRVS spectra, and their energy positions as well as intensities can be well reproduced via various theoretical calculations. Calculation of the NRVS is included in the ORCA quantum chemistry program package
[44]. In contrast, IR or Raman calculations often involve assumptions about molecular properties such as trail dipole moments or polarizabilities in order to obtain an approximate molecular PVDOS. In the rest of this article, unless mentioned otherwise, NRVS spectra refers to PVDOS.
Using
57Fe as an example, the nuclear scattering energy can be precisely selected by the extremely narrow 5 neV (= 5 × 10
−9 eV) natural linewidth of the nuclear back radiation (
hν1 in
Figure 1a). Meanwhile, the NRVS signal (lifetime on the order of nanoseconds) can be well separated from the electronic scattering (lifetime on the order of femtoseconds) in the time domain. Thus, NRVS does not need to extract the signal from background via a low-throughput diffraction spectrometer, such as in the case of inelastic X-ray scattering (IXS)
[45][46]. The time domain distinction makes NRVS spectra have higher signal throughput, an almost zero background, and with a true zero wave number (cm
−1) start, which in turn makes the measurement on extremely weak (0.1 counts per seconds or 0.1 cts/s) signal possible, such as the Fe–H–Ni vibrational peak
[19][36] in
Figure 1b. A 0 cm
−1 starting point is well illustrated in
Figure 1b (as well as subsequent figures). For various reasons, IR/Raman spectra often start from 80 cm
−1 instead. Due to the high throughput, e.g., in comparison with IXS, NRVS uses 1/10 of the incident beam flux but obtains 10 times of the signal level, which is perfect for measuring radiation-sensitive samples.
As NRVS spectra only show the vibrations associated with the isotope involved in the nuclear transition, e.g., 57Fe, the resulting vibrational spectrum is, thus, simpler and easier to be interpreted even without a theoretical simulation. For example, as illustrated in Figure 1b, various 57Fe–X bands can be identified. Fe–S is in the lower end of the spectra because Fe–S has a moderate interaction strength and S is heavier than C or H. On the other hand, Fe–H-related vibration is at an obviously higher-energy position because it has a stronger Fe–H interaction and a very light H mass. Since H has a very small mass, Fe–H vibrations will occur mainly at the H atom instead of the Fe atom, making its NRVS signal much smaller in comparison with Fe–S or Fe–CO (Figure 1b). These trends can be understood and rationalized even without theoretical simulation.
In the practical aspects, NRVS also has a number of compelling advantages over the established methods; for example, it is water-transparent in comparison with far-IR spectroscopy and, thus, well suitable for studies on biological samples in their natural environment or other samples in aqueous solution; it is free of fluorescence problems in comparison with resonance Raman spectroscopy (RR spectroscopy) and, thus, suitable for studies on photosensitive states/samples; it distinguishes well among O, N, and C ligands in comparison with X-ray crystallography or extended X-ray absorption fine structure (EXAFS). Therefore, in addition to its wide applications in physics and material sciences, NRVS is now the third modern X-ray spectroscopy technique, which has been widely welcomed by biochemical researchers, following X-ray crystallography and EXAFS.