
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Pluvinage Guy | + 839 word(s) | 839 | 2021-07-20 11:04:21 | | | |
| 2 | Ron Wang | + 154 word(s) | 993 | 2021-08-05 09:41:56 | | | | |
| 3 | Ron Wang | + 154 word(s) | 993 | 2021-08-05 09:42:29 | | |
Video Upload Options
The addition of hydrogen in natural gas degrades over time the materials of transport and storage. This degradation depends on the ratio of hydrogen natural gas. After addition, several criteria need to be assessed: In the following, the hydrogen embrittlement (HE) effect on design, maintenance and surveillance of smooth and damaged gas pipes is presented.
1. Introduction
However, hydrogen carrier still faces several limitations: − A large amount of energy is necessary for storage of hydrogen in compressed liquid or metal hydride form; − Transport is less efficient than that of oil or gas due to this low density when comparing energy transported per unit of volume; − Risks of detonation and flammability with air; − Production process cost, particularly water electrolysis, remains high; − For hydrogen cars, the establishment of a network of hydrogen stations requires considerable time and investment.
The range is similar to that of a diesel vehicle: a full tank of hydrogen in a 700-bar pressurized tank can travel up to 400 km, two to three times more than battery-powered cars.
The transport of hydrogen into the existing gas pipeline network has been proposed to increase the use of renewable energy systems [1].
The mixture of hydrogen and natural gas, in varying proportions of hydrogen not exceeding 20% by volume, supply the boiler room in the new district to meet the demand of about 100 homes.
2. Hydrogen Embrittlement
It has been recognized since the end of the 19th century that hydrogen alters the steel mechanical properties [2] by hydrogen embrittlement (HE). To unlight this phenomenon, tensile tests on API L X52 pipe steel have been performed and presented in Figure 1 . Specimens are loaded by an electrolytic process for HE and in air. One notes a reduction in failure elongation (38%) and a small reduction in yield stress and ultimate strength, respectively, 3.8% and 7.4%, as well as a reduction in fracture toughness. This phenomenon was first discovered by Johnson [2]. There was also a reduction in fracture resistance.
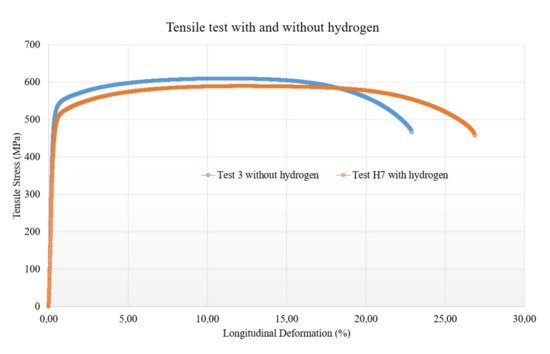
Degradation of toughness increases the risk of gas line failure, loss of life, environmental damage, and economic loss associated with the repair of affected lines and loss of production.
Hydrogen embrittlement affects fatigue crack propagation in stage II (Paris law regime) and particularly carbon pipe steels. Crack growth rate versus the maximum amplitude of the stress intensity factor in natural gas is presented in Figure 2 by the solid line curve.
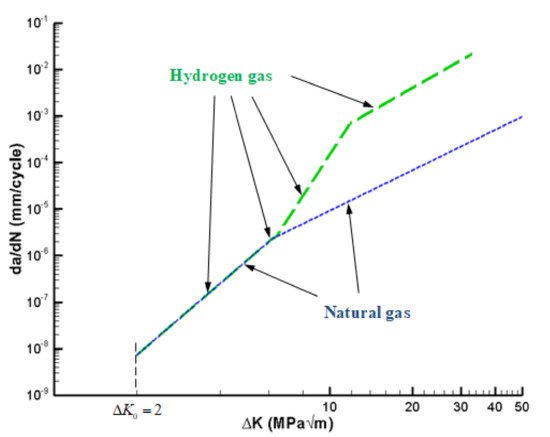
The process is made up of three stages: − In the beginning, the growth rate increases along the sigmoidal curve governed by the fatigue crack threshold K TH , step 1. An increase in fatigue crack growth is attributed to hydrogen diffusion at the crack tip.
3. Design Factor for Smooth Pipe Transporting Hydrogen Blended with Natural Gas
According to the pipe steel and service pressure, the design factor is used for the determination of pipe diameter.
This is valid only for pipe geometry and steel API 5L X60. A larger study on other pipe geometry and steels could not strongly modify the conclusion.
The coefficient of variation (COV) of the steel yield stress is incorporated in Equation (9). Therefore, the design factor is sensitive to the COV of material properties. Figure 3 presents the influence of yield stress COV on MAOP. This figure indicates that, for an urban area, the MAOP decreases by 90% and the design factor by 85% when COV vary in the range [0.05–0.20].
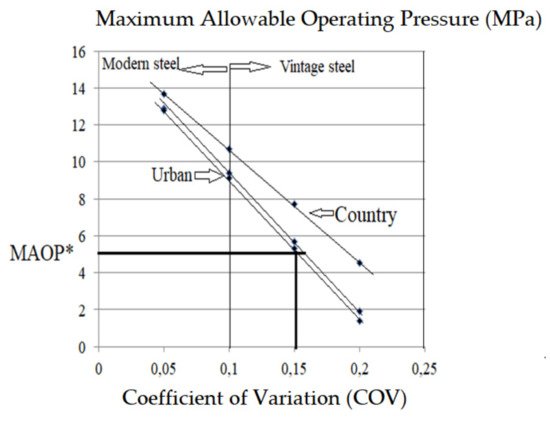
If we assume that that the economical threshold for MAOP, called MAOP* is 50 MPa, one cannot tolerate in the pipe networks, some part with vintage steels exhibiting a COV greater than 0.15, see Figure 3 .
4. Corrosion Defect Harmfulness after HE
Flow stress σ 0, α parameter and, Folias correction M are different according to the applied method (see Table 1 ).
| Method | σ0 (MPa) | α | Folias Correction M |
|---|---|---|---|
| B31G | 1.1 σy | 2/3 | - |
| B31G | 1.1 σy | 1.0 | ∞ |
| Modified B31G | σy + 69 MPa | 0.85 | - |
| Modified B31G | σy + 69 MPa | 0.85 | - |
| DNV-RP-F101 | σul | 1.0 | - |
| API RP-579 | σy/0.9 | 1.0 | - |
A pipe made from API 5L X52 steel with a corrosion defect is submitted to internal pressure. The pipe diameter is D = 611 mm and the thickness t = 11 mm t. This corrosion defect is considering as equivalent to an internal semi-elliptical crack (aspect ratio a/c = 0.5 and relative crack depth a/t = 0.5). Applied J integral is computed with the true stress/strain with and without HE of API 5L X52 pipeline steel.
The defect assessment (for a relative crack depth a/t = 0.1) is situated in the limit analysis domain when the material is not submitted to, HE. When submitted, the assessment point is situated in the LEFM domain.
The safety factor for the limit analysis domain is defined as: (19) f s ,LA = p s / p l where p l the limit pressure (according to ASME B31 [3]) and p s is the service pressure. In Table 2 , values of the safety factor for different relative defect depth ratios (a/t = 0.1 to 0.5), two different gas pressures as well hydrogen embrittlement are reported. F s ,LA is calculated when the loading path is situated in the LA domain, i.e., for the relative defect depth a/t = 0.1; 0.2 and 0.3. The safety factors decrease when the applied pressure increases. HE induces a decrease in f s by less than 10%. The safety factor associated with LA is always greater than the LEFM one. It decreases when the relative defect depth increases.
| fs | pap = 5 MPa | pap = 11 MPa | ||||
|---|---|---|---|---|---|---|
| a/t | without HE (EPFM) |
without HE (LA) |
with HE (EPFM) |
without HE (EPFM) |
without HE (LA) |
with HE (EPFM) |
| 0.1 | - | 3.47 | 3.70 | - | 1.58 | 1.67 |
| 0.2 | - | 3.47 | 3.23 | - | 1.58 | 1.47 |
| 0.3 | - | 3.47 | 2.78 | - | 1.58 | 1.27 |
| 0.4 | 2.63 | - | 2.33 | 1.18 | - | 1.04 |
| 0.5 | 2.17 | - | 2.00 | 0.98 | - | 0.89 |
References
- Vries, H.; Mokhov, A.V.; Levinsky, H.B. The impact of natural gas/hydrogen mixtures on the performance of end-use equipment: Interchangeability analysis for domestic appliances. Appl. Energy 2017, 208, 1007–1019.
- Johnson, W.H. On some remarkable changes produced in iron and steel by the action of hydrogen and acids. Proc. R. Soc. Lond. 1875, 23, 168–179.
- ASME B31G-1991. Manual for Determining the Remaining Strength of Corroded Pipelines; The American Society of Mechanical Engineers: New York, NY, USA, 1991.




