Your browser does not fully support modern features. Please upgrade for a smoother experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Zhen-wu WANG | + 3183 word(s) | 3183 | 2021-07-13 09:00:46 | | | |
| 2 | Amina Yu | Meta information modification | 3183 | 2021-07-20 06:07:08 | | |
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Wang, Z. Nature-inspired optimization algorithms. Encyclopedia. Available online: https://encyclopedia.pub/entry/12212 (accessed on 07 February 2026).
Wang Z. Nature-inspired optimization algorithms. Encyclopedia. Available at: https://encyclopedia.pub/entry/12212. Accessed February 07, 2026.
Wang, Zhen-Wu. "Nature-inspired optimization algorithms" Encyclopedia, https://encyclopedia.pub/entry/12212 (accessed February 07, 2026).
Wang, Z. (2021, July 20). Nature-inspired optimization algorithms. In Encyclopedia. https://encyclopedia.pub/entry/12212
Wang, Zhen-Wu. "Nature-inspired optimization algorithms." Encyclopedia. Web. 20 July, 2021.
Copy Citation
Over previous decades, many nature-inspired optimization algorithms (NIOAs) have been proposed and applied due to their importance and significance. Some survey studies have also been made to investigate NIOAs and their variants and applications. However, these comparative studies mainly focus on one single NIOA, and there lacks a comprehensive comparative and contrastive study of the existing NIOAs.
nature-inspired algorithm
meta-heuristic algorithm
swarm intelligence algorithm
bio-inspired algorithm
black-box optimization benchmarking
statistical test
1. Introduction
Nature-inspired optimization algorithms (NIOAs), defined as a group of algorithms that are inspired by natural phenomena, including swarm intelligence, biological systems, physical and chemical systems and, etc. [1]. NIOAs include bio-inspired algorithms and physics- and chemistry-based algorithms; the bio-inspired algorithms further include swarm intelligence-based and evolutionary algorithms [1]. NIOAs are an important branch of artificial intelligence (AI), and NIOAs have made significant progress in the last 30 years. Thus far, a large number of common NIOAs and their variants have been proposed, such as genetic algorithm (GA) [2], particle swarm optimization (PSO) algorithm [3], differential evolution (DE) algorithm [4], artificial bee colony (ABC) algorithm [5], ant colony optimization (ACO) algorithm [6], cuckoo search (CS) algorithm [7], bat algorithm (BA) [8], firefly algorithm (FA) [9], immune algorithm (IA) [10], grey wolf optimization (GWO) [11], gravitational search algorithm (GSA) [12] and harmony search (HS) algorithm [13]. In addition to the theoretical studies of NIOAs, many previous works have made an in-depth investigation on how the NIOAs are applied to various domains. Single NIOAs have been reviewed comprehensively [14][15][16][17][18][19][20][21][22][23][24][25], which present the algorithms and their variants at a good breadth and depth. In the rest of this chapter, we summarize the current survey work of the NIOAs, discuss our motivations for this survey, present our research methodologies and scope of this work and finally, describe our contributions to this field.
2. Common NIOAs
Actually, most of the NIOAs have a similar structure, although they are defined in various forms. In this section, first, the common process will be extracted to offer a unified description for the NIOAs, and then the principles of the 11 NIOAs will be outlined and discussed under this unified structure. The unified representation makes it convenient to analyze the similarity and dissimilarity of these algorithms.
2.1. The Common Process for the 11 NIOAs
The common process of most of NIOAs is described in Figure 1, which can be divided into four steps. In step S1, the population and related parameters are initialized. Usually, the initial population is generated by random methods, which ensure it covers as much solution space as possible; the population size is selected based on expert experience and specific requirements, and generally, it should be as large as possible. Most NIOAs use iterative methods, and the maximum iteration times and precision threshold are two common conditions of algorithm termination, which should also be initialized in step S1.
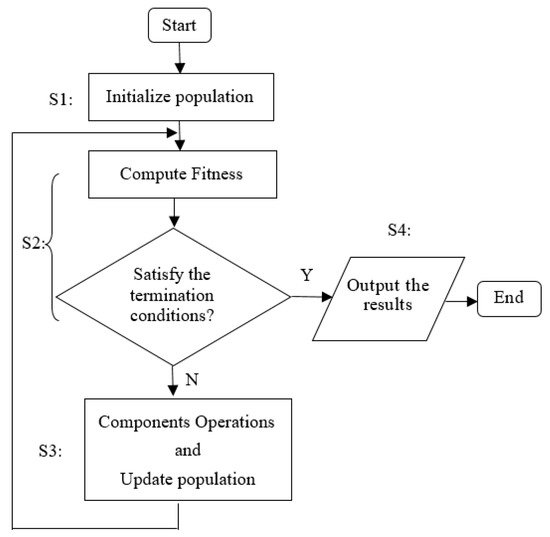
Figure 1. The common process of NIOAs.
The fitness function is the unique indicator that reflects the performance of each individual solution, and it is designed by the target function (i.e., the BBOB functions will be described in Section 4.1), which usually has a maximum or minimum value. Generally, an individual has its own local optimal solution, and the whole population has a global optimum. In step S2, the fitness values of the population in each iteration are computed, and if the global best solution satisfies the termination conditions, NIOAs will output the results (in step S4). Otherwise, step S3 is implemented, which performs the key operations (defined by various components or operators) to exchange information among the whole population in order to evolve excellent individuals. Then, the population is updated, and the workflow jumps to step S2 to execute the next iteration. According to the above process, a set of commonly used symbols are given in Table 1 as a unified description for the 11 NIOAs, where D represents the dimension number of objective functions, M is the individual number of each NIOA and N the total iterative times.
Table 1. The common symbols of NIOAs.
| Conceptions | Symbols | Description |
|---|---|---|
| Space dimension | D, 0<d≤D | The problem space description |
| Population size | M, 0<i≤M | Individual quantity |
| Iteration times | N, 0<t≤N | Algorithm termination condition |
| Individual position | xi(t)=(xi,1(t),…,xi,d(t),…,xi,D(t)) | The expression of the ith solution on the tth iteration, also used to represent the ith individual |
| Local best solution | pi(t)=(pi,1(t),…,pi,d(t),…,pi,D(t)) | Local best solution of the ith individual on the tth iteration |
| Global best solution | pg(t)=(pg,1(t),…,pg,d(t),…,pg,D(t)) | Global best solution of the whole populationon the tth iteration |
| Fitness function | f(⋅) | Unique standard to evaluate solutions |
| Precision threshold | δ | Algorithm termination condition |
3. Theoretical Comparison and Analysis of the 11 NIOAs
3.1. Common Characteristics
As shown in Section 2, although the NIOAs simulate different population behaviors, all of them are the iterative methods and have some common characteristics which satisfy the Reynolds model [26] and this model describes the basic rules for the aggregation motion of the simulated flock created by a distributed behavioral model.
1. Randomicity. Randomicity is the uncertainty of an event with a certain probability and can enhance the global search capability of individuals. All the 11 NIOAs initialize individuals randomly, which can cover the space as large as possible, some other mechanisms have been adopted in them which can enhance the exploration and exploitation abilities, such as the mutation operators mo in GA, IA and DE, the random parameters rand1 and rand2 in PSO, rand(0,1) and φ in ABC, βi and ε in BA, εi in FA, Lévy flight in CS, rand and randj in DE, randj and randi in GSA, r1, r2,A1, A2, A3 and C1, C2,C3 in GWO, u(−1,1) in HS, etc.
2. Information Interactivity. The individuals in the NIOAs should exchange information directly or indirectly, which can increase the probability of obtaining the global optimum. For instance, GA, IA and DE adopt the crossover operator co to exchange information; for PSO, each particle utilizes the global optimum pg(t) to update its position; employed foragers or onlookers in ABC update their velocities vi,d(t+1) using another different position xj,d(t); bats in BA use global optimum pg(t) to update their positions; in FA, firefly xi(t) moves toward xj(t) through mixing the positions information of xi(t) and xj(t); as to GSA, the force Fdi,j(t) is computed according to the positions of particles xi(t) and xj(t), which are used to update the position of each particle; the wolf in GWO updates its position according to the positions of wolves α, β and δ; and at last but not least, a new harmony in HS is generated from HM.
3. Optimality. The individuals in the NIOAs move toward the global best solution through different mechanisms of information exchange. For example, the good genes in GA and DE are chosen as the next generation through the operators so, co and mo; particles in PSO update their positions, influenced by the local optimum pi(t) and the global optimum pg(t); onlookers in ABC choose the food sources that have better fitness than the old one, the bat in BA generates a new solution and updates its position only if the new solution is better than the old one; the good antibodies in IA would save in a memory database to participate in the next iteration; as to FA, one firefly moves toward the fireflies that have larger luminance; CS replaces solutions only when the new one is better than the chosen solution and a fraction of worse solutions will be replaced by the newly generated solutions; in GSA, the gravitational and inertial masses are calculated by the fitness evaluation and the better individuals have higher attractions and walk more slowly; wolves in GWO update their positions according to the positions of wolves α, β and δ, which have better solutions in the wolf population; and a new harmony vector in HS can replace the old harmony in HM only if the new harmony is better than the old one.
In addition to the aforementioned common characteristics of theoretical implementation, these common NIOAs are varied to different versions to handle different problems, including combinational optimization problems (COPs) and multi-objective optimization problems (MOOPs). Similar variant methods are adopted to improve the optimization performance of NIOAs, for example, adaptive technology, fuzzy theory, chaos theory, quantum theory and hybridization technology. The classic articles about the above work are listed in Section 3.2, which provides a comprehensive summary of the 11 different NIOAs.
4. Challenges and Future Directions
Indeed, how to improve the performance of NIOAs is a very complex problem, which is influenced comprehensively by the methods of parameter tuning, topology structure and learning strategy. In this study, we draw some preliminary conclusions in order to provide a referencing framework for the selection and improvement of NIOAs. In the past 30 years, a large number of meta-heuristic algorithms (more than 120 in our statistics) and their variants have been proposed in order to provide efficient and effective solutions to optimization problems in the field of AI. Although great progress has been made on the NIOAs, which have been widely and successfully applied to various application fields, challenging problems still exist, mainly reflected in the following four aspects.
1. The first one is the lack of sufficient research in fundamental theories and tools of NIOAs. From our observation, the challenges of the fundamental researches on NIOAs include the following four points.
(1) The biological or natural mechanisms imitated by the NIOAs are not yet fully clear. Most of the NIOAs are proposed by the experts of psychology or computer science and engineering, and close collaboration with biologists is extremely important in order to deeply understand and abstract such mechanisms and functions so that NIOAs can be reasonably and effectively integrated into nature, biology and the real environment.
(2) It is also necessary to lay a solid foundation of mathematical theories to support NIOAs. Such examples include a rigorous time complexity analysis and convergence proof, a deep analysis of topological structures of various NIOAs, a suitable and comprehensive theoretical explanation to balance the contradiction between easily falling into local optimum and slow convergence speed, and an in-depth analytic study of the methods of automatic parameters tuning in order to solve the parameter-dependence problem. Specifically, while working on classic fundamental works [27][28][29] with some achievements in time complexity analysis and convergence proof, the researchers give a list of future research directions, which we brief as follows: for topology analysis, it is indicated that the local neighborhood topology for some specific algorithm is more suitable for complex problems [30], and the investigation into the PSO paradigm finds that the effect of population topology interacted with the function is optimized [31]. Although these previous efforts have recommended population topologies, they still have not precisely identified the topological factors that may result in the best performance on a range of functions [31]. An automatic tuning process for parameters is usually computationally expensive, especially for real-world application problems; therefore, it is desirable to have a benchmark test that suits the NIOAs’ tuning toolbox and is easy to use [32]. Due to the lack of a solid mathematical foundation, almost all the NIOAs are working under the black-box mode; thus, there are always researchers proposing so-called “novel” algorithms and declaring that their optimizers find better solutions than other NIOAs [33].
(3) The research is not sufficient on the problem extension of basic continuous NIOAs to different optimization problems, including COPs and MOOPs. The study here on different learning strategies and topological structures of more than 120 MHAs can provide diverse solutions to COPs and MOOPs. Actually, the current research of mathematical theories in the aforementioned (2) and problem extensions mainly focus on a few NIOAs, including GA, PSO and DE, so it is required to pursue further research to more NIOAs.
(4) Another problem is the visualization platforms of NIOAs research. From our observation, there are few discussions on this aspect except for an early simple attempt [34]. In addition, few benchmark tests suit specific optimization problems such as automatic parameter tuning [32]. Owing to the insufficient and inadequate theoretical investigation on the NIOAs, it becomes quite difficult to clearly distinguish the characteristics of different NIOAs (most of the algorithms look very similar) and this, per se, becomes another optimization problem of an optimal selection of the NIOAs for a given problem. This is also a motivation that we attempt to compare and analyze 11 common NIOAs theoretically and experimentally.
2. The second one is that NIOAs are less capable of solving continuous optimization problems in complex environments. The real environments are complicated, and the optimization problems can be high-dimensional, large-scale, multi-modal and multi-objective; the optimization environments can be dynamic, highly constrained and uncertain; the fitness evaluations may contain noises, be imprecise and time-consuming, and sometimes the fitness functions can be un-deterministic. The complexity of the real environments poses a great challenge to NIOAs. Although some efforts [35][36][37] have been made to solve the aforementioned problems, how to handle these issues is still a very difficult problem.
3. The third one is too few combinations of NIOAs with other related disciplines. NIOAs intrinsically have a parallel and distributed architecture, while less attention is paid to the combinations with parallel and distributed technologies, including GPU-based hardware, robot swarm and cloud platforms. A few works [38][39][40] focus on the above issues, and interdisciplinary research is a great potential for NIOAs.
4. The fourth one is that less effort has been made to apply NIOAs to various domain problem fields. Actually, on the one hand, it is impossible to have one single NIOA to adapt to all the application problems. On the other hand, a certain kind of NIOAs may be more effective for certain kinds of problems [41]. Existing enhanced methods of NIOAs (for example, a combination of different NIOAs) lack an in-depth and targeted discussion on the reason why the enhanced methods are adopted. Furthermore, various NIOAs have been adopted to handle the same application problem, but it is not clear why this NIOA was chosen (researchers just happened to use it).
Consequently, it is our belief that in the future, researchers should tackle the following three problems in the NIOAs. These three problems indicate three future research directions for the NIOAs study.
1. Strengthening solid theoretical analysis for the NIOAs. Some theoretical problems of NIOAs are only studied in specific NIOA (for example, PSO), such as the time complexity analysis, the convergence proof, topology analysis, the automatic parameter tuning, the mechanisms of the exploitation and exploration processes. There are still many problems to be solved in the existing research work [27][28][29], and the theoretical analysis of other NIOAs needs to be analyzed deeply. COPs and MOOPs should be further studied by extending and combining the various existing NIOAs. Furthermore, it is necessary to develop a visualization platform of deconstructing, modeling and simulation of the interactions of components in NIOAs, to make it convenient to study the mechanisms of self-organization, direct/indirect communication and the processes of intelligent emergence on various swarm systems and application cases. It is also necessary to establish a benchmark test suite and easy-to-use algorithm toolbox for different problems, for example, automatic parameter tuning and the aforementioned problems in complex environments.
2. Designing novel NIOAs to solve complicated optimization problems. Many real-world optimization problems are very complex, such as the multi-model and multi-objective problems, the constrained or uncertainty problems, the large-scale optimization problems, the optimization problems with noisy, imprecise or time-varying fitness evaluations. It is another important direction to design more targeted and effective NIOAs for the above problems.
3. Deep fusion with other related disciplines. In order to improve the performance of the current NIOAs, it is indispensable to combine the NIOAs with other related disciplines or directions, such as distributed and parallel computing, machine learning, quantum computation and robot engineering. More concretely, because NIOAs by nature possess the characteristics of distributed parallelism, it is more easily and natural for them to be implemented in distributed and parallel environments, such as cloud platforms and GPU-based hardware environments. Furthermore, for some large-scale optimization problems, the robot swarm can be a good solution that combines NIOAs and robot engineering. With the support from machine learning methods, NIOAs can become efficient to handle the multi-modal multi-objective optimization problems, and on the other way around, NIOAs can provide optimization support to machine learning tasks, such as the clustering problem and the association rules mining problem.
4. Combination with specific applications. It is necessary to design customized NIOA for specific application problems; the topological structure, learning strategy and method of parameters’ selection of customized NIOAs may be suitable to a specific problem, which can acquire the good convergence speed and optimization performance. Existing applications rarely have targeted design of NIOAs; more of them use NIOAs directly or cannot explain the reason for algorithm design with specific problems.
5. Conclusions
Nature-Inspired Optimization Algorithms (NIOAs) can provide satisfactory solutions to the NP-hard problems, which are difficult and sometimes even impossible for traditional optimization methods to handle. Thus, the NIOAs have been widely applied to various fields both theoretically and in practice; examples including function optimization problems (convex, concave, high or low dimension and single peak or multiple peaks), combinatorial optimization problems (traveling salesman problem (TSP), knapsack problem, bin-packing problem, layout-optimization problem, graph-partitioning problem and production-scheduling problem), automatic control problems (control system optimization, robot structure and trajectory planning), image-processing problems (image recognition, restoration and edge-feature extraction), data-mining problems (feature selection, classification, association rules mining and clustering).
Many NIOAs and their variants have been proposed in the last 30 years. However, for the specific optimization problems, researchers tend to choose the NIOAs based on their narrow experiences or biased knowledge because there lacks an overall and systematic comparison and analysis study of these NIOAs. This study aims to bridge this gap; the contributions of this paper are fourfold. First, we summarize the uniform formal description for the NIOAs, analyze the similarities and differences among the 11 common NIOAs; second, we compare the performance of 11 NIOAs comprehensively, which can reflect the essential characteristics of each algorithm; third, we present a relatively comprehensive list of all the NIOAs so far, the first attempt to systematically summarize existing NIOAs, although it is very hard work; fourth, we comprehensively discuss the challenges and future directions of the whole NIOAs field, which can provide a reference for the further research of NIOAs. Actually, we are not aiming to find a super algorithm that can solve all problems in different fields once and for all (it is an impossible task). Instead, we propose a useful reference to help researchers to choose suitable algorithms more pertinently for different application scenarios in order to take a good advantage and make full use of the different NIOAs. We believe, with this survey work, that more novel-problem-oriented NIOAs will emerge in the future, and we hope that this work can be a good reference and handbook for the NIOAs innovation and applications.
Undoubtedly, it is necessary and meaningful to make a 34 comprehensive comparison of the common NIOAs, and we believe that more efforts are required to further this review in the future. First, the state-of-the-art variants of the 11 common NIOAs will be compared and analyzed comprehensively, discussing their convergence, topological structures, learning strategies, the method of parameter tuning and the application field. Second, there are more than 120 MHAs with various topological structures and learning strategies. For example, the recently proposed chicken swarm optimization (CSO) and spider monkey optimization (SMO) algorithms have a hierarchical topological structure and grouping/regrouping learning strategies. Thus, the comprehensive analysis of various topological structures and learning strategies of NIOAs is another future work.
References
- Fister, I., Jr.; Yang, X.S.; Brest, J.; Fister, D. A Brief Review of Nature-Inspired Algorithms for Optimization. Elektrotehniški Vestn. 2013, 80, 116–122.
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975.
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the 1995 IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948.
- Storn, R.; Price, K. Differential Evolution-A Simple and Efficient Heuristic for Global Optimization over Continuous Space. J. Glob. Opt. 1997, 11, 341–359.
- Dervis, K.; Bahriye, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471.
- Colorni, A.; Dorigo, M.; Maniezzo, V. Distributed optimization by ant colonies. In Proceedings of the 1st European Conference on Artificial Life, York, UK, 11–13 November 1991; pp. 134–142.
- Yang, X.S.; Deb, S. Cuckoo Search via Lévy Flights. In Proceedings of the 2009 World Congress on Nature and Biologically Inspired Computing, Coimbatore, India, 9–11 December 2009; pp. 210–214.
- Yang, X.S.; Gandomi, A.H. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012, 29, 464–483.
- Yang, X.S. Nature-Inspired Metaheutistic Algorithms; Luniver Press: Beckington, UK, 2008.
- Bersini, H.; Varela, F.J. The Immune Recruitment Mechanism: A Selective Evolutionary Strategy. In Proceedings of the International Conference on Genetic Algorithms, San Diego, CA, USA, 13–16 July 1991; pp. 520–526.
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61.
- Esmat, R.; Hossein, N.P.; Saeid, S. GSA: A Gravitational Search Algorithm. Inform. Sci. 2009, 179, 2232–2248.
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68.
- Lim, T.Y. Structured population genetic algorithms: A literature survey. Artif. Intell. Rev. 2014, 41, 385–399.
- Rezaee Jordehi, A. Particle swarm optimisation for dynamic optimisation problems: A review. Neural Comput. Appl. 2014, 25, 1507–1516.
- Dervis, K.; Beyza, G.; Celal, O.; Nurhan, K. A comprehensive survey: Artificial bee colony (ABC) algorithm and applications. Artif. Intell. Rev. 2014, 42, 21–57.
- Chawla, M.; Duhan, M. Bat Algorithm: A Survey of the State-Of-The-Art. Appl. Artif. Intell. 2015, 29, 617–634.
- Dasgupta, D.; Yu, S.H.; Nino, F. Recent Advances in Artificial Immune Systems: Models and Applications. Appl. Soft Comput. 2011, 11, 1574–1587.
- Fister, I., Jr.; Yang, X.S.; Brest, J. A comprehensive review of firefly algorithms. Swarm Evol. Comput. 2013, 13, 34–46.
- Mohamad, A.B.; Zain, A.M.; Bazin, N.E.N. Cuckoo search algorithm for optimization problems—A literature review and its applications. Appl. Artif. Intell. 2014, 28, 419–448.
- Swagatam, D.; Suganthan, P.N. Differential evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2011, 15, 4–31.
- Esmat, R.; Elaheh, R.; Hossein, N.P. A comprehensive survey on gravitational search algorithm. Swarm Evol. Comput. 2018, 41, 141–158.
- Dorigo, M.; Blum, C. Ant colony optimization theory: A survey. Theor. Comput. Sci. 2005, 344, 243–278.
- Hatta, N.M.; Zain, A.M.; Sallehuddin, R.; Shayfull, Z.; Yusoff, Y. Recent studies on optimisation method of Grey Wolf Optimiser (GWO): A review (2014–2017). Artif. Intell. Rev. 2019, 52, 2651–2683.
- Alia, O.M.; Mandava, R. The variants of the harmony search algorithm: An overview. Artif. Intell. Rev. 2011, 36, 49–68.
- Reynolds, C. Flocks, herds, and schools: A distributed behavioral model. Comput. Graph. 1987, 21, 25–34.
- He, J.; Yao, X. Drift analysis and average time complexity of evolutionary algorithms. Artif. Intell. 2001, 127, 57–85.
- Mohammad Reza, B.; Zbigniew, M. Analysis of Stability, Local Convergence, and Transformation Sensitivity of a Variant of the Particle Swarm Optimization Algorithm. IEEE Trans. Evol. Comput. 2016, 20, 370–385.
- Mohammad Reza, B.; Zbigniew, M. Stability Analysis of the Particle Swarm Optimization Without Stagnation Assumption. IEEE Trans. Evol. Comput. 2016, 20, 814–819.
- Chen, W.N.; Zhang, J.; Lin, Y.; Chen, N.; Zhan, Z.H.; Chung, H.S.H.; Li, Y.; Shi, Y.H. Particle Swarm Optimization with an Aging Leader and Challengers. IEEE Trans. Evol. Comput. 2013, 17, 241–258.
- Kennedy, J.; Mendes, R. Population structure and particle swarm performance. In Proceedings of the 2002 Congress on Evolutionary Computation, Honolulu, HI, USA, 12–15 May 2002; pp. 1671–1676.
- Huang, C.W.; Li, Y.X.; Yao, X. A Survey of Automatic Parameter Tuning Methods for Metaheuristics. IEEE Trans. Evol. Comput. 2020, 24, 201–216.
- Soerensen, K. Metaheuristics—the metaphor exposed. Int. Trans. Oper. Res. 2015, 22, 3–18.
- Hart, E.; Ross, P. GAVEL—A New Tool for Genetic Algorithm Visualization. IEEE Trans. Evol. Comput. 2001, 5, 335–348.
- Ryoji, T.; Hisao, I. A Review of Evolutionary Multimodal Multiobjective Optimization. IEEE Trans. Evol. Comput. 2020, 24, 193–200.
- Ma, X.L.; Li, X.D.; Zhang, Q.F.; Tang, K.; Liang, Z.P.; Xie, W.X.; Zhu, Z.X. A Survey on Cooperative Co-Evolutionary Algorithms. IEEE Trans. Evol. Comput. 2019, 23, 421–440.
- Jin, Y.C.; Wang, H.D.; Chugh, T.; Guo, D.; Miettinen, K. Data-Driven Evolutionary Optimization: An Overview and Case Studies. IEEE Trans. Evol. Comput. 2019, 23, 442–458.
- Djenouri, Y.; Fournier-Viger, P.; Lin, J.C.W.; Djenouri, D.; Belhadi, A. GPU-based swarm intelligence for Association Rule Mining in big databases. Intell. Data Anal. 2019, 23, 57–76.
- Wang, J.L.; Gong, B.; Liu, H.; Li, S.H. Multidisciplinary approaches to artificial swarm intelligence for heterogeneous computing and cloud scheduling. Appl. Intell. 2015, 43, 662–675.
- De, D.; Ray, S.; Konar, A.; Chatterjee, A. An evolutionary SPDE breeding-based hybrid particle swarm optimizer: Application in coordination of robot ants for camera coverage area optimization. In Proceedings of the 1st International Conference on Pattern Recognition and Machine Intelligence, Kolkata, India, 20–22 December 2005; pp. 413–416.
- Li, Z.Y.; Wang, W.Y.; Yan, Y.Y.; Li, Z. PS-ABC: A hybrid algorithm based on particle swarm and artificial bee colony for high-dimensional optimization problems. Expert Syst. Appl. 2015, 42, 8881–8895.
More
Information
Subjects:
Physics, Mathematical
Contributor
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
8.8K
Revisions:
2 times
(View History)
Update Date:
11 Nov 2021
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No




