1000/1000
Hot
Most Recent

Sound waves are a form of energy transmission in the mechanical vibration state of an object. Ultrasound is a type of sound wave with a vibration frequency higher than 20 kHz, which cannot be heard by humans. A piezoelectric ultrasonic transducer (PUT) is a device for achieving mutual conversion of mechanical energy and electrical energy. Due to the advantages of high safety and low cost, a PUT has been widely used as the core device for non-destructive testing (NDT), medical imaging, particle manipulation, and flow measurement. The traditional optimization design methods are mainly based on an analytical model, an equivalent circuit model, or a finite element model and the design parameters are adjusted by a trial-and-error method, which relies on the experience of experts and has a relatively low efficiency. Recently, by combining intelligent optimization algorithms, efficient optimization design methods for a PUT have been developed based on a traditional model or a data-driven model, which can effectively improve the design efficiency of a PUT and reduce its development cycle and cost.
Sound waves are a form of energy transmission in the mechanical vibration state of an object. Ultrasound is a type of sound wave with a vibration frequency higher than 20 kHz, which cannot be heard by humans [1]. A piezoelectric ultrasonic transducer (PUT) is a device for achieving mutual conversion of mechanical energy and electrical energy [2].
Due to the advantages of high safety and low cost, a PUT has been widely used as the core device for non-destructive testing (NDT), medical imaging, particle manipulation, and flow measurement [3][4][5][6]. In NDT, ultrasonic detection and the guided-wave structural health monitoring (SHM) method are combined to detect the damage of wind turbine blades, and the defect position can be precisely determined [7]. The annular PUT array printed by three-dimensional (3D) printing technology has adjustable focal domain and resolution and has been successfully used for NDT [8]. In medical imaging, the piezoelectric performance of a PUT is improved by polarizing to achieve high imaging resolution [9]. In addition, the inaccuracy of transcranial imaging caused by phase aberration can be eliminated by using ultrasonic adaptive beam forming to make ultrasonic imaging more accurate [10]. An acoustic radiation force optical coherence tomography system, using integrated micro ultrasound and optical coherence tomography, can map the correlated elasticity of vascular tissue to aid medical diagnosis [11]. In particle manipulation, the accurate control of ultrasound is extremely important for non-contact manipulation of biologics and bioanalysis [12]. Single-beam acoustic tweezers with pressure-focusing technology can be used as the manipulators in a wide range of biomedical and chemical sciences [13]. In addition, a bending PUT has been widely used for flow measurement under atmospheric pressure conditions [14]. A flexible piezocomposite ultrasound transducer can continuously measure blood pressure by tracking the ultrasonic motion of the vessel wall, and it can be used for non-invasive, non-obstructive, calibration-free blood pressure and blood flow monitoring [15]. Therefore, a PUT is the key component in specific ultrasonic application systems, and its performance mainly affects the performance and effectiveness of these systems.
Traditional optimization design methods for a PUT are developed based on an analytical model, an ECM, or a FEM, and the design parameters are determined by using a trial-and-error method, which is inefficient and depends on the knowledge of experts. Efficient and intelligent optimization design methods for a PUT are proposed and developed based on intelligent optimization algorithms. In the efficient optimization design methods, a traditional model or a data-driven model is used to describe the relationships among design and performance parameters of a PUT.
A simple and efficient optimization design method for a PUT can be developed by combining the traditional models and intelligent optimization algorithms. The traditional models can characterize the effects of design parameters on the performance of a PUT, and the intelligent optimization algorithms are utilized to optimize the design parameters.
Using CIVA software, Puel et al. [16] constructed a multiobjective optimization function for the optimization design of a PUT, and the evolutionary algorithm was used to optimize the design parameters, as shown in Figure 1A. According to the required performance of detection, the CF, size, and kerf of element could be optimized by the developed method. According to the principle of sound field, Choi et al. [17] proposed a mathematical model to describe the acoustic field distribution, as shown in Figure 1B. Then, the design parameters of a concave annular high intensity focused ultrasonic transducer could be optimized by using a nonlinear programming algorithm, which was beneficial for fabricating a high-intensity focused ultrasonic transducer. By combining an ECM and the particle swarm optimization (PSO) algorithm, Chen et al. [18] developed an optimization design method for PUT (as shown in Figure 1C). According to the optimized design parameters, the fabricated PUT had a CF of 6.3 MHz and a −6 dB bandwidth of 68.25%. With the combination of topology optimization and a FEM, Rubio et al. [19] designed a functional gradient PUT, (Figure 1D). The design parameters of the functional gradient PUT were optimized by using a topological optimization algorithm, which effectively improved the performance of the PUT.
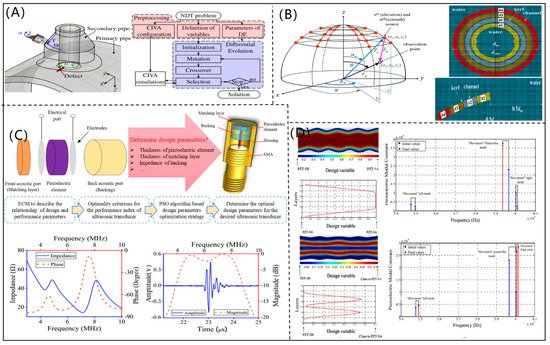
Figure 1. (A) Evolutionary algorithm-based optimization design method for a piezoelectric ultrasonic transducer (reproduced from [16]); (B) mathematical model for a concave annular high intensity focused ultrasonic transducer and its finite element model (reproduced from [16]); (C) optimization design for a piezoelectric ultrasonic transducer using the particle swarm optimization algorithm (reproduced from [17]); (D) functionally graded piezoelectric ultrasonic transducer optimized by using the topological optimization algorithm (reproduced from [18]).
Due to the simple and fast calculations of an analytical model and an ECM, they can be easily combined with an intelligent optimization algorithm to design a PUT, but only several design parameters can be optimized due to the limitations of the analytical model and ECM. Although a FEM can be combined with an intelligent optimization algorithm to design a PUT, the design efficiency is very low because a FEM is very time-consuming.
Due to the limitation of traditional models, the optimization design of a PUT cannot be designed in an efficient or comprehensive way. A data-driven model is established based on data and can be used to accurately and quickly describe the relationships among design and performance parameters, which can effectively improve the optimization design efficiency for a PUT.
On the basis of a genetic algorithm-based back-propagation neural network (GABPNN) model and the PSO algorithm, Chen et al. [20] proposed an optimization design method for a high-performance transmitting PUT (shown in Figure 2A). The GABPNN models were trained using the data simulated by PiezoCAD software to describe the relationships among the design and performance parameters of the PUT, and the PSO algorithm was adopted to determine the design parameters. The CF and insertion loss of the designed PUT were 1.07 MHz and 7.2 dB, respectively, which had excellent transmitting performance. In addition, Chen et al. [21] designed a 1-3 piezocomposite ultrasonic transducer for imaging application based on a data-driven model and modified PSO algorithm. As shown in Figure 2B, the ultrasonic images showed that the designed 1-3 piezocomposite ultrasonic transducer had high resolution and good signal-to-noise ratio. On the basis of intelligent optimization algorithms, Li et al. [22] designed a PUT with multi-match layers, as shown in Figure 2C. The CF, –6 dB bandwidth, and pulse width of the designed PUT were 5.672 MHz, 50.08%, and 0.295 us, respectively, which were significantly better than those of the PUTs without a matching layer. Additionally, the testing error of five-step block thickness was less than 1.0%.

Figure 2. (A) Optimization design method for a high-performance transmitting piezoelectric ultrasonic transducer (reproduced from [20]); (B) designed and fabricated 1-3 piezocomposite ultrasonic transducer for ultrasonic imaging (reproduced from [20]); (C) optimization design method for a piezoelectric ultrasonic transducer with multi-match layers and testing results (reproduced from [21]).
In order to effectively and flexibly control the acoustic field, Li et al. [23] proposed an efficient optimization design method for an acoustic liquid lens (as shown in Figure 3A) under the PSO framework. Tungsten wires and porcine eye were imaged by the 6 MHz PUT with an optimized acoustic liquid lens, and the ultrasonic imaging quality was obviously improved, which verified the reliability and effectiveness of the developed method. As shown in Figure 3B, Sun et al. [24] proposed an intelligent optimization design method for matching layers of a PUT. The neural network models were trained to establish the mapping relationships among the thicknesses of matching layers and performance parameters of the PUT. An improved PSO algorithm was used to optimize the thicknesses of matching layers (Ag-epoxy and parylene C). It was found that the PUT with the optimized matching layers had a −6 dB bandwidth of 68.5% and pulse echo width of 0.123 us, which were superior to those of the PUT with matching layers determined by the traditional quarter-wavelength theory.
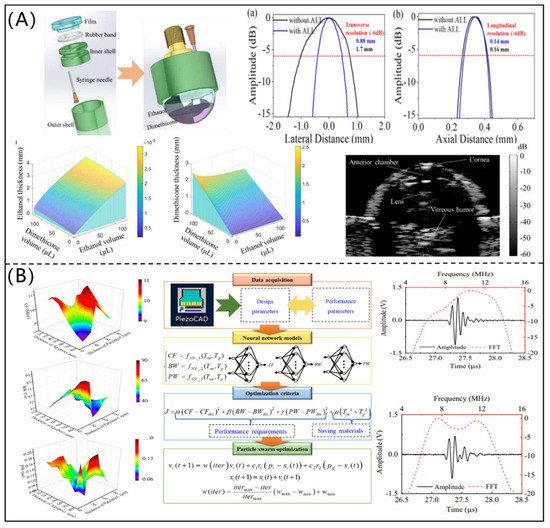
Figure 3. (A) Acoustic liquid lens and ultrasonic imaging results of porcine eye (reproduced from [23]); (B) Effect of matching layers on the performance of a piezoelectric ultrasonic transducer, and the intelligent optimization design of piezoelectric ultrasonic transducer with two matching layers (reproduced from [23]).
In the efficient optimization design method, a data-driven model can be established to represent the relationships among the design parameters and the performance parameters of a PUT, and an intelligent optimization algorithm is used to determine the design parameters. This method is relatively efficient and can reduce the design cycle and cost for a PUT. However, a large amount of data should be obtained and accumulated to establish the data-driven model, and therefore the data acquisition is the key for this method.