1. Introduction

Cell membranes are self-assembled structures formed by lipids and proteins, and constitute a complex and constantly changing environment. The strength of the inter-molecular interactions defines the mechanical properties of these quasi-bidimentional systems, and these interactions may be Van der Waals forces (Keesom, Debye and London interactions ^[1]), hydrogen-bonding, and/or forces between permanent charges, dipoles or higher multipoles. It is clear that these last forces are electrostatic, but in truth all other forces of interaction also have an electrostatic origin, inflicted in essence by the charged nature of fundamental particles. Thus, electrostatics commands membrane mechanical properties.

Electrostatic forces amongNparticles are led by a simple equation, Coulomb law:

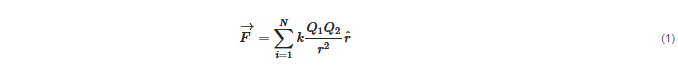
Since electrostatic forces are additive, all electrostatic interactions in a system can be accounted for using this equation if the position of all charges are known. This apparently rather simple task involves the summation (or integration in case of charge densities) of all charges at each position which may turn out extremely complicated, depending on the spacial distribution of the charges.

An important parameter in Equation (1), which is included ink, is the local dielectric constant in the proximity of each charge. In the case of lipid bilayers, the dielectric constant varies from a value close to 80 (in the internal and external aqueous milieu) to a value close to 2 (in the bilayer interior). In the region of the polar headgroups, an intermediate value is expected that depends on the lipid class and phase state. In lipid monolayers, values in the range of 5–20 have been determined ^[2].

Cell membranes contain lipids and proteins, and thus different values ofεare expected along the membrane plane. In the regions of the membrane enriched with lipids, values close to 2 are expected in the middle of the bilayer and values close to that determined in lipid monolayers/bilayers for the region of the polar head groups. However, the dielectric constant of cytoplasm may be very different from 80 since water is not free to move but ordered inside cells due to molecular crowding, as has long been noted by different authors ^[3][4]. Furthermore, water order varies during cell metabolism ^[5] and, as all properties in cell interior, it is very likely to vary from a region to the other inside cells.

Experimental determinations ofεin the cell interior have been performed in yeast, yielding values in the range 50–60 ^[6][7][8]. Values of ~60 have been found for erythrocytes ^[9], and ~70 for T-lymphocytes ^[10] and for viral tegument ^[11]. Authors suggested that the combined effects of several organelles may be responsible of the reported large value.

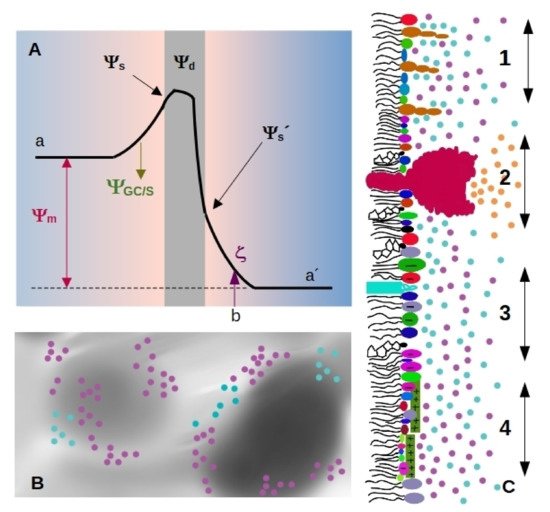
Four important electrostatic potentials can be described in biological membranes, which are schematized in Figure 1A ^[12][13]: The difference between these values is called membrane, transmembrane or diffusion potential Ψm^[12], see Figure 1A (we will use the term membrane potential forΨmthroughout the review). The presence of highly ordered molecules with a charge distribution characterized by a dipole or higher order multipoles inside the membrane, as well as a lower dielectric constant in the membrane interior compared to the surface, gives rise to a non-zero potential inside the membrane called dipole potential Ψd^[13]. These charges in turn interact with small ions or charged molecules from the solution, resulting in an ion cloud around the membrane.

The diffuse layer contains small anions and cations, including protons. In turn, pH defines ionization of acid and basic polar head-groups and thereby the membrane charge density. Therefore, there is a strong interdependence between membrane ionization and composition of the aqueous milieu close to the membrane ^[14][15][16].

Since membrane composition is not constant, dielectric constant and charge density are expected to vary from a region to the other, as schematized inFigure Therefore, each region of the membrane may bear different values ofΨs and Ψd(Figure 1C), which affect local interactions and thus, diffusional properties of the species within the membrane, local compressibility and bending, and local interaction between membrane and soluble charged species. Among them, we can state melting temperature and phase state, local curvature, stiffness, and bending. Therefore, how emergent properties in membranes behave upon environmental changes is an open question.

2. Surface Charge Density, Surface and Zeta Potentials

Depending on the particular membrane, 10 to 40% of the lipids are negatively charged. Cationic lipids such as sphingosine and psychosine are uncommon and are present in healthy cells in a very low proportion. Both, anionic and cationic species lead to non-zero surface charge density, and to the presence of an ion cloud close to the surface whose density varies within the characteristic distanceλD(close to one nanometer at physiological conditions).

In general, the increase in surface charge density tends to expand the molecular area ^[16]. Since lipid area is related to membrane phase state, the temperature for phase transitions depends on the membrane charge density, and therefore is affected by the proportion of charged lipids in the membrane as well as by ionic strength ^[16][17]. Given that each phase state is characterized by its particular mechanical properties, it is expected that electrostatics influences the viscoelastic response of membranes upon different stresses. Aside from changes related to phase transitions, many other effects have been reported as detailed in the following sections.

Surface charge density can be studied by means of electrophoretic mobility, which gives information about electrostatics at the hydrodynamic plane of shear (slipping plane, SP). This plane is located at a distancedSPfrom the membrane surface, marked asbin Figure 1A). The potential at this point is called zeta-potential (ζ), and depends on Ψ8, the drop in electrostatic potential due to adsorbed ions (Stern model), and screening by the ion cloud (Gouy-Chapman model).

However,dSP is not known with precision even though some estimations have been reported. A distance of 0.2 nm from the membrane surface was postulated early in 1979 by the group of McLaughlin for phosphatidylserine or phosphatidilglycerol vesicles in solutions containing alkali metal cations ^[18]. In another set of experiments, McLaughlin et al. claimed thatdSPchanges with ionic strength, going from 0.2 nm for 0.1 M to 1 nm for 0.001 M NaCl ^[19]. for phosphatidilcholine/cholesterol vesicles in 0.01 M KCl ^[20].

Considering that the diameter of a water molecule is about 0.2–0.3 nm ^[21][22], and that lipid membranes are not atomically flat, a value fordSPlower than the nm appears very small. Furthermore, lipids with a bulky polar headgroup (such as GM1) mixed with small charged headgroups will generate a surface roughness larger than the distance attributed to SP position as schematized in Figure 1C ^[19]. In this regard, Woodle et al. found that incorporation of pegylated phosphatidylserine (polyethylene glycol attached to the polar headgroup of the lipid) into bilayers produces a substantial negative surface potential, but an electrophoretic mobility lower than expected. This was explained considering an increase in the hydrodynamic radius due to steric effects of polyethylene glycol moieties ^[23].

For instance, the affinity of cationic peptides to anionic membranes can be obtained fromζdeterminations ^[24] Therefore,ζdeterminations will yield lower values than Ψ8(seeFigure 1A). Besides, it has been shown thatζdoes not vary linearly with ionic strength ^[25], meaning that variations ofζdo not always change proportionally to changes inΨs. Therefore,ζwill better reflect surface potential in solutions of low ionic strength, which are unfortunately not physiologically relevant conditions.

3. Effects of Ions Different from Protons

The association of cations to membrane surfaces occurs both, on anionic and zwitterionic lipid bilayers. The extent of binding is greater for charged interfaces due to the increased cation concentration in the ion cloud near the lipid surface, according to the Gouy-Chapman theory.

There is a general trend that cations bind stronger to ordered than to disordered lipid phase states in anionic membranes. This is due to the smaller mean molecular areas in the ordered phases, leading to larger surface charge densities and consequently more negative surface potentials. However, the relationship between ion affinity and molecular area is intricate, because ionizable lipid density (and the consequent charge density and surface potential) in turn modulates lipid ionization fraction ^[16]. Furthermore, the dependence of the intrinsic affinity of cations to the surface charge density is non-linear, evidencing that besides the unspecific electrostatic interactions, cation-bilayer binding is also mediated by specific interactions ^[26][27].

The influence of ion binding on the mechanical properties of membranes is mainly due to changes in lipid packing. On one hand, cation binding may increase the fraction of ionized polar head groups due to changes in the pKa value as stated inSection 3, leading to an expansion in the lipid molecular area, which stabilizes fluid phases. On the other hand, cations preferentially bind to lipid ordered phases, as already mentioned. This is due to two factors: an unspecific electrostatic association to membranes with higher charge density, that leads to lipid molecular area shrinkage due to membrane charge screening (only for anionic membranes), and a specific polydentate coordination to some functional group of the lipid polar moiety, which may be present in both, charged and zwitterionic membranes.

Evaluation of hydration levels of lipid polar head groups by polarized infrared spectroscopy indicated that the interaction of Li+, and divalent cations Be2+, Mg2+, Ca2+, Sr2+, Ba2+, Zn2+and Cu2+stabilizes the gel phase, and consequently increases the melting temperature. Mg2+, Ca2+, Sr2+and Ba2+render lipid carbonyl groups more accessible to water because they interact mainly at the phosphate groups level in the gel phase, dehydrating it. Conversely, Be2+, Zn2+and Cu2+dehydrate carbonyls, as well as phosphate groups ^[27].

The mechanical stability of lipid membranes in the presence of different ions was assessed by atomic force microscopy (AFM) in the force spectroscopy mode, testing the response of phospholipid bilayers under compression. An increase in the mechanical stability with the affinity of the adsorbed ions and ionic strength was observed, due to lipid compaction caused by the screening of the interlipid electrostatic repulsion. In the case of compact bilayers, the Van der Waals interactions between lipid acyl chains are maximized increasing cohesion of the membrane. The effect is higher in the gel phase than in the liquid crystalline phase, and it is sensitive to the ion size and charge.

Membrane rigidity upon bending, that can be quantified by the mean bending rigidity modulusκ, is partially determined by the surface charge density. Cation binding has a direct impact on surface charge density of anionic lipid bilayers, and consequently, on the mechanic properties of the membrane. In a regime of low ionic concentration, bothκandRdecrease with the ionic strength, due to a decrease of the Debye length, since the deformation of the double layer bears most of the energy cost of bending the membrane. Together with ion dehydrating effect on the bilayer, this leads to thicker and stiffer membranes with increasing ionic strength.

The interaction of these ubiquitously distributed monovalent ions with polar head groups of phospholipid aggregates shows relevant effects in lateral organization, including phase segregation in palmitoyloleoylphosphatidylcholine membranes in the presence of NaCl ^[28]. This is due to complexation of sodium ions by tight interaction with lipid carbonyl groups with a mean coordination number of three ^[29]. It was postulated that this kind of deep coordination can take place in the case of H3O+ions as well, explaining previous observation of proton long residence times ^[30][31]. The interaction between Na+ions and phosphatidylcholine membranes leads to membrane structural changes such as a 5 % increase in membrane thickness.

K+cations at anionic membrane interfacial region was performed combining single-ion level AFM with molecular dynamics simulations ^[32]. While sodium ions adsorb strongly to lipid carbonyl oxygens, in an unstructured thick layer, potassium organizes into two discrete coordination layers, separated by a bridging water layer. The slow kinetics of ionic networks evolution inside the nanodomains due to electrostatic interactions and the hydration water molecules that compete for the polar head groups, locally reduce the effective stiffness of the membrane. In fact, the formation of clusters of ion-bridged lipids through C=O groups has shown to overcome charge repulsion and leads to counterintuitive smaller average areas for anionic lipid compared to neutral analogs ^[33].

Both these activities are related to its mechanism of interaction with negatively charged lipids, where it induces negative spontaneous local curvature. This was evidenced by the formation of invaginations on GUVs composed of phosphatidylserine and phosphatidylinositol-bisphosphate, upon Ca2+asymmetry across the membrane at sub-millimolar concentration, likely due to Ca2+-induced lipid clustering ^[34]. Membrane remodelling was also attained with Mg2+and Na+ions, but with millimolar and tens of millimolar transmembrane gradients requirements respectively, due to the higher energetic cost for ion dehydration. The weak effects promoted by Mg2+were also attributed to its small size, that is not enough to perturb lipid intermolecular distance as Ca2+^[35].

The interaction of Ca2+with anionic lipids such as phosphatidic acid and its derivative diacylglycerol pyrophosphate, which are in turn involved in signaling pathways themselves, is characterized by lipid clustering and membrane stiffening, as demonstrated using Langmuir films ^[36]. Ca2+binding interacts in an 1:1 stoichiometry with singly-charged di-basic phosphatidic acid, decreasing the second acidic pKa and forming a neutral lipid:Ca(II) complex ^[37]. However, the overall charge neutralizing effect compacts the film packing giving raise to stiffer membranes for pure diacylglycerol pyrophosphate monolayers, as well as for mixtures of diacylglycerol pyrophosphate and phosphatidic acid. These effects are pH-dependent, being more marked at basic pHs, where deprotonated lipids form expanded structures.

Zn2+has numerous roles as cofactor and structural stabilizer of diverse proteins. The interaction of Zn2+with model membranes was also sampled in monolayers of phosphatidic acid and diacylglycerol pyrophosphate ^[38]. Furthermore, Zn2+induces a phase transition in phosphatidic acid films from a liquid-expanded to a liquid-condensed state, not observable in the absence of the ion. The effect is sensitive to pH, being more marked at acidic pHs.

Since the strong condensation effect driven by binding of divalent cations on lipid film surfaces may induce phase transition to ordered phase states, these ions can be considered potent regulators of membrane structure. The regulatory mechanism is finely tuned by cation affinity to membranes. The interplay of lipid molecular area and membrane charge density, that leads to ion adsorption/desorption due to membrane phase and structure changes, originates local gradients of ions concentrations ^[16][39].

Other very important cation-membrane interaction that is worth mentioning in this review is that between membranes and cationic peptides. Peptides rich in basic aminoacids have shown a high affinity for membranes, which depends on anionic lipids content ^{[40][41][42][43][44][45][46][47]}, membrane dipole potential ^[45][48] (seeFigure 2A), membrane phase state ^[49] and chemical composition ^[45][50][51].

Many of such peptides remodel membrane structure facilitating self- and cargo-permeation, a property that confers them the name of cell-penetrating peptides (CPP). These peptides allow the introduction of small molecules inside cells ^[52]. The translocation mechanism of CPPs involves membrane softening, leading to membrane protrusion, pore formation or membrane leakage ^[52][53].

Another family of cationic peptides is that of the antimicrobial peptides (AMPs). They are part of many living organisms immune response, and their antibiotic activity relies on the drastic impact their association has on the membrane structure and integrity ^[54]. Although treated differently by people interested in CPPs or AMPs, the ability to reach the inner leaflet of lipid bilayers is crucial to both of them. In fact, potentially, all CPPs are AMPs and all AMPs are CPPs, and “membrane-active peptides” (MAPs) would be a better and more inclusive name for all of them ^[55].

The peptide-induced interfacial remodelling is a combination of electrostatic and topological effects, and this grants many MAPs selectivity to tumor cell membranes rich in glycosaminoglycans ^[56], and towards microbial over mammalian membranes ^[41].

Figure 2B,C show examples of membrane softening determined in GUVs for a CPP (B) and an AMP (C). Membrane thinning, and in turn softening, has been proposed to be due to hydrophobic matching between peptide and membrane ^[57]. Surface entropy of membrane-bound peptides has also been considered ^[58]. Peptides that are adsorbed at, or inserted in the membrane, may form clusters ^[59], and induce structural rearrangements of the lipids around them ^[60].

Membrane stiffening due to peptide binding can also be explained considering curvature effects in the membrane due to MAP-lipid structures ^{[61][62][63][64]}. Zemel et al. used a molecular-level chain packing theory ^[65], and found that the curvature stress depends on the penetration depths of the peptide. Interesting, despite thinning of the membrane upon peptide insertion, they found an increase in the bending stiffness.

In addition to the electrostatic-induced adsorption of MAPs to anionic membranes, specific peptide-membrane interactions have been reported, which depend on the aminoacid: polylysine and polyarginine behave differently. Although negative curvature is induced when the polypeptide inserts in the membrane, polyarginine induces simultanueously a positive curvature along one principal direction resulting in a negative Gaussian curvature and a saddle-shapped deformation. This was attributed to the bridging of multiple lipid headgroups by bidentate complexation of arginine with phospate groups ^[66].

Decoupling of the two leaflets of the bilayer due to peptide insertion has also been considered to account for membrane softening ^[67]. Furthermore, the formation of hydrophilic pores was considered by Grasso et al., who found, using all atom molecular dynamics simulations that water penetration promoted by MAPs leads to a local decrease of the lipid order, which emerges macroscopically as a reduction of the membrane bending modulus ^[68].

Lipid recruiting due to a selective interaction of the peptide with a particular lipid class has also been considered ^[49][69]. Related to this, a theoretical model was proposed that considers electrostatic interactions between MAPs and anionic lipids, leading to membrane disruption ^[70]. MAPs are proposed to adsorb electrostatically at the membrane interface, and subsequently insert at the lipid head group-tail interface, screening charged lipid-lipid electrostatic repulsion, and inducing an average shrinkage in their molecular area, thus reducing the average area of one of the hemilayers, and originating curvature.

Despite membrane softening due to the interaction with cationic peptides is well reported, and it is accepted that electrostatic interactions play a fundamental role in the interaction, not much discussion about a direct correlation between electrostatics and membrane mechanical properties is found in literature, being the work of Cahill an interesting exception ^[71]. In this article, the transient pores induced by CPPs are compared to electroporation (seeSection 5.2), and a model of transduction is proposed in which phosphatidylserines and CPPs form two plates of a capacitor with a voltage sufficient to form pores due to electroporation ^[71].

4. Potentials across Membranes

Potential-induced membrane deformation due to ionic gradients across the bilayer has been experimentally evidenced since late 1960s, when birefringence changes in the axon membrane of neurons was attributed to changes in the potential difference ^[72]. The electrical response of membranes to a mechanical deformation gives rise to piezoelectricity and flexoelectricity. While piezoelectricity refers to polarization due to uniform strain, flexoelectricity refers specifically to polarization due to strain that changes from point to point in the membrane. They are somehow interrelated as membrane curvature can arise from asymmetric changes in the area in one hemilayer relative to the other.

These phenomena are involved in membrane electromotility, whose magnitude and polarity depends on membrane stiffness and surface potential ^[73][74]. This is the origin of complex cellular functions such as mechanosensitivity and mechanotransduction of signals in the nervous system ^[74]. It is also responsible for electromotility that leads to mammalian hearing ^[74][75]. Besides understanding its physiological implications, flexoelectricity studies in biomembranes have a further impact on the development of engineering applications based on chemical biosensing ^{[76][77][78][79]}.

As pointed out previously, spontaneous curvature arises if there is charge asymmetry between membrane surfaces, due to either unequal charged lipid composition in each hemilayer, or ion gradient generated between both ionic diffuse layers. In the case of uniformly charged symmetric membranes, instability with respect to a spherical deformation has been proposed for highly charged membranes ^[80]. This explains the process of spontaneous vesiculation of ionizable membranes upon pH changes. close to the polar headgroups have been reported to depend on the curvature for inverse micelles, and also on the internal leaflet (negative curvature) of anionic liposomes ^[81].

The first experimental approach to study flexoelectricity in membranes was attained by AC currents registration on planar lipid bilayers subjected to a hydrostatic oscillating strain ^[82][83]. This group also made determinations of flexoelectricity in cell membranes applying the patch-clamp technique ^[84]. Voltage induced cantilever movement due to an imbalance in surface tension in the two hemilayers of the bilayer was modelled by Lippman equation ^[73][75]:(3)dγdΨs=−Γq whereγis the surface tension Relying on the capacitor model to approximate membrane behavior, Lippman equation integration yields:(4)γ=−12CDΨs2+γ0

γ0is the voltage independent tension This yieldsCD~30 F cm−2at physiological saline concentration ^[74]. The membrane is conceptualized as three serial capacitors: a Debye capacitance for the interfacial ion cloud at each side of the membrane, and a hydrocarbon capacitor in between, with a low capacitance ofCm~0.5 F cm−2. Even when neglecting ion adsorption to the membrane, hydration layers, and the discreetness of the charges (and thereby steric hindrance), it has proven to perform nicely on modelling electrical behavior in membranes and electromechanical coupling ^[85].

Main theoretical approaches to study flexoelectricity in membranes based on continuum models were inspired by the previous observation. al have derived a continuum model to describe the electromechanical effect of the application of a static potential across the membrane ^[86]. These calculations yielded a positive contribution of the electric field to the bending rigidity, and negative contribution to the membrane tension, implying that an applied potential makes the membrane stiffer towards bending and with lower surface tension. This arises from the balance of the free energy contributions due to the compression and expansion of the charge densities at both sides of the bilayer, with opposite sign and different magnitude, and gives rise to the cost aforementioned of bending the ion cloud along with the membrane.

Despite the success of the continuum approach derived by Ambjörnsson et al., Harland et al. reported flaws in performance in continuum models, thus evidencing that electromechanical coupling can be commanded by voltage-dependent discreet adsorption of ions to the phospholipid polar head groups ^[87]. Neglecting the discreteness of charges leads to lower values for the flexoelectric coefficients compared to experimental values ^[84]. Even when the obtainedfresulted smaller than the experimental ones, the flexoelectric effect evidenced by continuum models remained qualitatively satisfactory. Dynamic coupled effects such as viscoelasticity, neglected as well in continuum models, could further contribute to the discrepancies observed.

External applied voltages induce mechanical modifications in membranes that can be predicted understanding membrane flexoelectricity and piezoelectricity properties. These mechanical changes in the lipid bilayer are in turn responsible for protein conformational modulation of ion channels and transporters ^[88].

The effects promoted by external potentials are not different from those related to intrinsic membrane potentials arising from the dipolar nature of the amphiphiles, membrane asymmetries and ion imbalance across the bilayer ^[89]. There is however a consideration that has to be made in relation to the orientation of the external potential relative to membrane orientation. While membrane potentials keep isotropic symmetry across the membrane all along the interface, external potential adds up depending on the relative local orientation of the membrane ^[90]. For spheroidal membranes, a uniform externally applied field would vary in intensity and even in sign along the membrane.

This electrostatic field-induced transient increase in permeability of cell membranes is known as electroporation and is largely used to introduce small molecules into the cell interior ^{[91][92][93][94][95][96][97]}. Loading of cells in suspension by applying voltage pulses involves large electric fields in the aqueous electrolyte (of the order105V/m for mammalian cells of 10 m). Since a uniform applied potential affects whole cells with variable intensity and directionality, the effect of a pulse in cells depends on the cell geometry. Bacteria are about an order of magnitude smaller than mammalian cells, and require a field around ten fold larger in order to induce similar increases in membrane permeability ^[94].

Cell membranes are much more complex than a lipid bilayer structure. However, when developing a model it is helpful to start from a simplified one, and the effect of protein inclusions in membrane electroporation is usually excluded, as the lipid bilayer appears to be responsible in electroporation phenomena. The most accepted model considers the existence of transient aqueous pores, with a probability of existence that depends on thermal energy and on the cost of pore formation ^[98]. Therefore, membrane mechanical properties play an important role in electroporation: deformability of membrane can affect the direction of water penetration ^[99] and lateral compressibility affects the free energy of pore formation since when the pore is created, its environment is compressed ^[100].

External potential increases the probability of formation of hydrophilic pores due to a decrease in the energy required for their formation, which is a consequence of changes in the membrane capacitance as pores are filled with water of higher dielectric constant than lipid, among other factors ^{[90][98][101]}. Therefore, in the presence of the electric field, poration rate increases and thereby, membrane permeability.

Additionally, molecular dynamics simulations indicate that the external field can cause rearrangements of ions, hydration water and polar headgroups, leading to more frequent water protrusions into the hydrophobic core of the membrane as compared to the unperturbed case. Water molecules eventually span the whole bilayer and a pore is formed ^[102]. Electrically induced chemical changes of membrane lipids or proteins may also contribute to the increase in bilayer’s permeability ^[96]. In this regard, it has been demonstrated that the electric field indirectly facilitates lipid oxidation in liposomes

It was shown that the threshold potential for electroporation of a membrane depends not only on its capacitance and dipole potential but also on the nature of lipids’ hydrophobic tails and polar headgroups, an interesting summary of the findings can be found in ref. Other sterols and also hopanoids decrease membrane permeability ^[103], but their effect on electroporation has not been systematically studied. Regarding polar headgroup, increases in the proportion of negatively charged lipids in a membrane increases the rate of pore formation ^[104]. In relation to phase state, it has been observed that pores form in the disordered phase in membranes with phase separation ^[105], and even when forcibly created in the ordered phase, they migrate to the disordered one ^[95].

Mechanical changes coupled to the changes in membrane potential have been reported over many years using a wide variety of techniques and cell types. The authors introduced a bundle of three olfactory nerves of garfish into a water-tight chamber, and measured rapid changes in the hydrostatic pressure with a mechanoelectric transducer. They observed that nerves undergo rapid volume expansion while carrying an impulse, due to lateral expansion of the excited portion of the fibers, where the superficial layer is transformed into a low-density structure. Zhang et al. used AFM to record dynamic membrane displacements in voltage-clamped human embryonic kidney cells ^[73].

The group of Anvari developed an experimental setup that combines optical tweezers with patch-clamp. Using optically trapped beads, they detached the plasma membrane from the cytoskeleton and formed membrane tethers, and determined forces at piconewton scale while changing membrane potential ^[106]. Using this approach, they measured electromechanical force generation by membranes of outer hair cells and human embryonic kidney cells ^[107]. They found that the mechanical properties of the membrane that determine the force required to pull and maintain membrane tether are a function of the transmembrane electric field.

All in all, it is beyond doubt that during the action potential, both the thickness and the area of the cell membrane change in comparison to the resting membrane, generating a density pulse. Furthermore, nonlinear pulses with the same characteristics as action potentials have been excited in phospholipid monolayers devoid of protein at the air-water interface ^[108]. Thus, electromechanical response of lipidic membranes is important and explains, at least partially, electric signal propagation in neurons, providing a useful model in neuroscience.

Related to the changes in membrane potential during the propagation of the electric pulse, the Hodgkin–Huxley model makes use of the Goldman–Hodgkin–Katz equation, which assumes that at rest, the net current flowing through the membrane is zero, and predicts that the membrane potential is commanded by the permeability of the membrane to each ion, which in turn governs ion fluxes. In contrasts to this interpretation, Tamagawa et al. proposed an alternative explanation, considering that ions adsorb at the membrane surface (without crossing it) ^[109]. As already stated inSection 4, ion affinity to the membrane depends on the particular ion and on the membrane composition. Besides, it varies with phase state, and according to Tamagawa et al., this would lead to changes in the membrane potential.