Protein Structure Prediction

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Sun Choi	+ 4049 word(s)	4049	2021-06-08 12:17:43

This entry is adapted from the peer-reviewed paper 10.3390/ijms22116032

The new advances in deep learning methods have influenced many aspects of scientific research, including the study of the protein system. The prediction of proteins’ 3D structural components is now heavily dependent on machine learning techniques that interpret how protein sequences and their homology govern the inter-residue contacts and structural organization. Especially, methods employing deep neural networks have had a significant impact on recent CASP13 and CASP14 competition. Here, we explore the recent applications of deep learning methods in the protein structure prediction area. We also look at the potential opportunities for deep learning methods to identify unknown protein structures and functions to be discovered and help guide drug–target interactions. Although significant problems still need to be addressed, we expect these techniques in the near future to play crucial roles in protein structural bioinformatics as well as in drug discovery.

structural bioinformatics deep learning protein sequence homology 3D structure of proteins drug discovery

1. Introduction

Proteins, large and complex polymers with linear amino acid chains, play crucial roles in cells responsible for constructing and regulating our body. By revealing the structure and contacts of biomacromolecules, we gain a better understanding of their function, thus facilitating the rational drug discovery process. The recent advances in experimental structural biology techniques such as X-ray crystallography, nuclear magnetic resonance (NMR), and cryogenic electron microscopy (cryo-EM) have fueled accurate structure determination ^[1]^[2]^[3]^[4]. However, owing to the high cost and time-consuming aspects of experimental determination, there is still a large “structure knowledge gap” between the vast amount of protein sequences and a relatively small number of known structures. Therefore, knowledge-based theoretical techniques to elucidate protein structure are in need. After Anfinsen’s dogma stating that the native structure of at least a small globular protein is determined by the sequence only, various attempts to identify protein structure from its sequence have been made, starting with predicting folding states of protein by Pauling and Corey in 1951 ^[5]^[6]^[7]. The significant breakthrough in next-generation sequencing (NGS) technology has led to burgeoning sequence information, and a fundamental problem in structural bioinformatics is predicting 3D structures using these tremendous sequence data ^[8].

Protein structure prediction has become more powerful and accurate with method developments from traditional statistical methods to machine learning (ML) and deep learning (DL) methods ^[9]^[10]^[11]. Artificial neural network, especially deep neural network, is a good fit for protein structure prediction with its ability to express a wide variety of functions and its efficiency relying heavily on the amount of quality data. The introduced concepts of homology and evolutionary information empowered the process, and the advent of robust equipment such as graphical processing unit (GPU) expedited it ^[12]^[13]^[14]. Initially, some pieces of protein structures such as helical status or torsional angles are targeted for prediction, and then the whole structure is deduced utilizing the predicted features known as protein structure annotations (PSAs) ^[15]^[16]. In order to catch up with recent progress and to know the state-of-the-art method, one can check with Critical Assessment of Structure Prediction (CASP), a worldwide community experiment held every two years to assess the effectiveness of prediction methods ^[17]^[18]^[19]. The usage of the artificial neural network not only saves time and cost, but also strengthens the functional analysis of large-scale proteomics studies. ML and DL technologies based on various computational methods enable the detection of protein–protein interaction (PPI) in heterogeneous types of proteomics data ^[20]. Multi-faceted analysis of protein structures can be linked to the prediction of drug–target interaction (DTI) ^[21]. As the application of deep learning methods to drug discovery areas is at a nascent stage, various machine and deep learning methods need to be considered and tested for better accuracy in analyzing PPIs.

In this review, we will provide an overview of DL-associated protein structure prediction, related concepts, frequently used DL architectures, and developed methods predicting various PSAs delineating different levels of details of protein structure. The further applications of DTI are of interest and discussed. Finally, current limitations, as well as the advantages of DL-based protein structure prediction upon drug discovery field, will be highlighted.

2. Protein Sequence Homology, 3D Structure, and Deep Learning

2.1. Protein Sequence Homology

The central dogma of molecular biology states that DNA sequences are transcribed into messenger-RNA (mRNA), and then these mRNA sequences are translated into protein sequences. Searching similar sequences can be used to reveal “homologous” genes or proteins by detecting statistically significant similarity, which indicates common ancestry. This protein sequence, in structural biology, is assumed to determine the three-dimensional structure and function of a protein. It is based on the fundamental observation that similar sequences from the same evolutionary family will typically adopt similar protein structures. Moreover, the structures of proteins are highly conservative in evolution compared with their sequences, and the number of unique structural folds is generally thought to be limited in nature. Thus, tremendous effort has been put into quarrying the relationship between structure and sequence of proteins. As the number of protein sequences is exponentially increasing, while the experimentally verified structures are growing slowly, we expect homology-based contact map prediction and modeling to become far more popular.

2.2. 3D Structural Space of Proteins

A protein structure can be defined as one of four levels: primary, secondary, tertiary, or quaternary structures. Primary structure is a linear sequence of amino acids. There are 20 standard amino acids available to form a protein, and each amino acid is connected to the next one via peptide bonds. Primary structure is often introduced as a string of letters, i.e., ‘AESVL…’, as each standard amino acid has a corresponding single-letter code (and three-letter code). This already gives much useful information with respect to protein structure in three-dimensional space owing to the distinctive characteristics of each amino acid. For example, the different hydrophobicity of each amino acid limits the conformation of the protein, and some unique covalent bonds can be formed only between certain amino acids such as cysteine. Many ab-initio protein structure predictions start with this sequence of amino acids, a primary structure.

Secondary structure defines the form of local segments of proteins. It is normally determined by the hydrogen bond patterns of polypeptide backbone or backbone dihedral angles (φ,ψ). The two common secondary structures are α-helices and β-strands. An α-helix is a segment of amino acids where the main chain forms a helix, pointing side-chains outward. Two hydrogen bonds per residue stabilize this helix formation. A β-strand is rather connected laterally where side chains are pointing out perpendicularly to the plane with each successive residue facing the opposite side. This form normally requires a partner β-strand unit for its stability. When used in protein structure prediction, secondary structure normally falls into a three-state or a fine-grained eight-state categorization. The three-state categorization consists of two regular types of α-helix (H) and β-strand (E), and one irregular type of coil region (C). The widely-used eight-state categorization based on the Dictionary of Secondary Structure for Proteins (DSSP) program by Sanders further dissect helices into three types as 3₁₀ helix (G), α-helix (H), and π-helix (I); strands into two types as β-strand (E) and β-bridge (B); and coils into three types as β-turn (T), high curvature loop (S), and any other previously undefined type (C) ^[22].

Tertiary and quaternary structures elucidate a three-dimensional arrangement of the single and multiple proteins, respectively. They can be represented using the Cartesian coordinates of each atom in three-dimensional space. Owing to the aqueous nature of proteins, the main driving force deciding tertiary and quaternary structure is the hydrophobic interaction among amino acids and water molecules. Thus, proteins tend to possess a hydrophobic core where side chains are buried, avoiding polar water molecules. Such three-dimensional information is deducible when one has the primary structure, secondary structure, and inter-residue CM in hand.

In contrast to sequences, which are virtually infinite in number, proteins can take on a finite number of different shapes to carry out their functions in the cell. One can observe stronger structural conservation than sequence conservation; for example, a strong interdependence for polar residues exists at protein core with poor solvent accessibility, but no significant correlation is detected when looking at sequences only ^[23]. This makes it feasible to predict protein structure, a more conserved domain, from abundant sequence data ^[24]. Hence, various attempts to unravel the relationship between the structure and sequence have been made, including deep learning methodologies and pre-eminent approximations for underlying mapping functions.

2.3. Overview of Deep Learning Methods

Deep learning is a branch of machine learning, utilizing an artificial neural network with many layers embedded, which resembles a human nervous system. Working as universal function approximators, deep neural networks are used to solve various problems: classification, clustering, pattern recognition, predictive analysis, regression, and so on ^[25]. With the rapid and tremendous growth of biomedical data sources, deep learning can be applied to multi-omics data analysis, disease categorization, and healthcare social network analysis. It indicates that high-quality data that are used to train and build deep learning models should be appropriately labelled for biomedical data analysis. When high-quality datasets are available for deep learning models, reproducible deep learning models can be built to analyze newly collected biomedical data of similar structures.

Artificial neural networks consist of nodes in input, output, and hidden layers where each node is connected to nodes in adjacent layers. These connections have distinct weights, and the inputs are processed (i.e., multiplication and summation) at each node. Then, it undergoes the transformation based on the activation function such as sigmoid or rectifier, and the output functions as the input for the next layer. Learning is the process of finding optimal weights that make the neural network behave as desired. Two types of learning are present; supervised learning handles labeled datasets for classifying or predicting purposes, while unsupervised learning handles unlabeled datasets for analyzing or clustering the given dataset. The amount of required training data to build effective deep learning models is dependent on the complexity and the number of features in the training data. To update and optimize the weights, back-propagation is used to calculate the gradient of the loss function that computes the error for each training iteration ^[26]. When too many layers are used, however, the gradients either vanish or explode, making the training process inefficient ^[27]. Certain tricks such as modifications upon activation functions (i.e., rectified linear unit (ReLU)) and utilizations of skip connections (i.e., residual neural network) exist to overcome this issue ^[28]^[29]^[30]. With these steps as a fundamental basis, there are miscellaneous architectures for artificial neural networks. With the expanding data availability for protein sequences and structures of closely related homologs, deep learning methods have been presented for protein structure prediction, and a few frequently used architectures will be discussed in this section (Figure 1).

Figure 1. Overview of deep learning (DL) architectures frequently used for protein structure prediction.

The most straightforward and earliest stage example for the deep neural network is the feedforward neural network (FFNN), sometimes called multilayer perceptron (MLP). A perceptron, a single-layer neural network, can only process first-order information to obtain results comparable to those obtained by multiple linear regression. When multiple layers are used, the neural networks can extract higher-order features. In FFNN, information flows in one direction from the input layer to hidden layers, if any, until it reaches the output layer. The network has connections between each node and every other node in the next layer.

Recurrent neural network (RNN) contains loops where the output of the layer becomes an input. This looping generates state neurons that enable the network to possess memory about the previous state. Obtaining a future memory is favorable for prediction and is feasible with RNN by introducing a delay, but the prediction rates drop if the delay is too large. To overcome this issue, a bidirectional recurrent neural network (BRNN) has been developed, splitting the state neurons into positive and negative time directions ^[31]^[32]. 2D-BRNN, a two-dimensional application of BRNN, has been widely used to correctly predict the residue contact map (CM), normally using four-state vectors handling four cardinal corners of the map ^[33]. Long-short term memory (LSTM) is a variant of unit cell used in RNN, designed to resolve vanishing gradient problems by introducing gate functions into the unit cell ^[34]. This error gating allows LSTM to learn long-term dependencies between data points. With their ability to permit sequence as inputs and outputs, RNNs are known for excellent performance upon any sequence-based problems, suitable for protein structure prediction with protein sequence as input.

Convolutional neural network (CNN) often encompasses three types of layers: convolutional, pooling, and fully connected layers ^[35]^[36]. CNN generally takes input such as a 2D image, and the convolutional layers apply various kernels to convolve it where each kernel acts like a perceptron, generating feature maps. Then, a pooling layer follows to perform dimension reduction upon the network parameters and feature maps. The results are forwarded into the fully connected layers, mapping 2D feature maps into a 1D vector for further feature representations. The main benefit of applying the convolution scheme is the massive parallelism, yielding a great amount of computational efficiency. Convolutional schemes are widely used for CM prediction, a 2D-PSA ^[37].

Graph deep learning models enjoy attention from numerous application domains thanks to their structural consistency to the native graph-structured data. Graph convolutional network (GCN), a generalization of the convolutional operator upon non-Euclidian structured data, contains several spectral or spatial convolutional layers ^[38]. Its unique featurization strategies at the input level with elaborated architectures suit complicated problems such as PPI or DTI.

To improve our fundamental understanding of biological phenomena, protein structures and their contacts shed light on their mechanism of action, possibly assisting with drug design. Based on the co-evolution analysis and deep learning methods, protein structure prediction methods have made significant progress in recent years by using multiple sequence alignments (MSAs) of the target protein and its homolog. A combination of the architectures mentioned above is widely used in this type of protein structure prediction methods. One famous example would be a combination of bidirectional RNN and CNN (BRNN–CNN) ^[39]. In this scheme, a convolutional kernel maps a window of BRNN memories into a local state. There exist variations such as bidirectional LSTM followed by CNN (BLSTM–CNN) ^[40]. Unlimited hybrid topologies are available, but one needs to design the architecture carefully, considering training difficulty, computational complexity, and memory requirement in order to obtain the best accuracy.

3. Prediction of 1D and 2D Protein Structural Annotations

Proteins and their functions are distinguished by their structures in numerous aspects, but the rate of discovering protein structures has been much slower than the rate of sequence identifications owing to the cost and complexity. Therefore, protein structure predictor has become one of the most efficient and high-throughput tools in Bioinformatics to handle flooding known sequence data with developing methodologies such as statistical, ML, and DL methods. The feature used in the predicting process is known as PSA; it contains simplified information to ease the computing process and is used as an intermediate step to estimate the full protein structure. One dimensional- (1D-) and two-dimensional- (2D-) PSAs have enjoyed a great amount of attention, where secondary structure, solvent accessibility, or intrinsic disorder is mainly described as 1D-PSA, and CM or the detailed version of CM (multi-class CM or distance map) is expressed with 2D-PSA. Several DL applications have been developed for 1D- and 2D-PSA predictions, becoming more accurate owing to expanding of the availability of sequence and structure data.

3.1. 1D Prediction

The most fruitful feature among 1D-PSAs is the secondary structure, the very first step for the full protein structure prediction from the sequence. Two main classifications are available: three-state categorization into α-helix, β-strand, and coil region, or eight fine-grained categorizations, which further segregate the previous three states (vide supra). The earlier stage methods have used sequence data solely as input sources, but later, evolutionary information and physicochemical properties were involved in enhancing the prediction accuracy ^[41]. The accuracy can be easily expressed by three-state percentage accuracy (Q₃ score) or eight-state percentage accuracy (Q₈ score), which is defined as the percentage of correctly predicted secondary structure residues.

One of the earliest servers available for secondary structure prediction would be JPred developed by Cuff et al. ^[42]. The server adopts six different secondary structure prediction algorithms: DSC using linear discrimination, PHD using jury decision neural networks, NNSSP using nearest neighbors, PREDATOR using hydrogen bonding propensities, ZPRED using conservation number weighted prediction, and MULTIPRED using consensus single sequence method combination ^[43]. 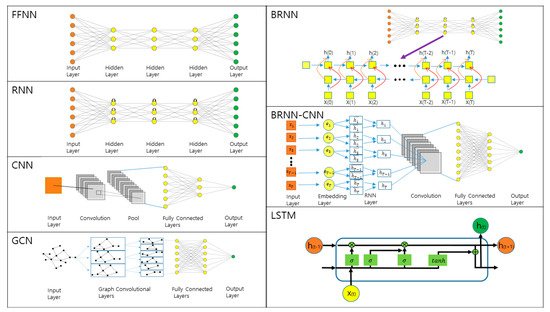Another secondary structure prediction server, PSIPRED, became available, where the method conjugates two FFNNs, training neural networks upon evolutionary conservation information derived from PSI-BLAST ^[44]^[45]. Another attempt called SSpro showed an enhanced algorithm application, using BRNN–CNN ^[46]. The method utilizes a mixture of estimators that leverages evolutionary information, indicated in multiple alignments, both at input and output levels of BRNN. Porter, Porter+, and PaleAle among the Distill series are also based on ensembles of BRNN–CNN, each used to predict different 1D-PSAs (Porter for secondary structure prediction, Porter+ for local motif prediction, and PaleAle for residue solvent accessibility prediction) ^[47]. In the following Distill methods, the sequence is processed by the first BRNN–CNN stage and then pulled into a set of averages, which are processed by the second BRNN–CNN stage. Porter achieved better performance using both PSI-BLAST and HHBlits for harnessing evolutionary information ^[48]^[49]. Likewise, Porter+ considers local structural motifs for predicting torsional angles ^[50]. PaleAle, dealing with relative solvent accessibility (RSA), is structured with double BRNN–CNN stacks in the most recent version of 5.0, surpassing benchmarks from other methods for RSA prediction ^[51]. NetSurfP-2.0, concatenating CNNs and BRNNs, was developed in 2019. This method predicts secondary structures, solvent accessibility, torsion angles, and intrinsic disorder, all at once ^[52].

Taking other 1D-PSAs into account along with secondary structure and considering physicochemical properties, as well as evolutionary information, helped to enhance the overall accuracy. DESTRUCT, proposed by Wood and Hirst, iteratively used cascade-correlation neural networks upon both secondary structure and torsional angles ^[53]. The iteration is composed of the first FFNN trained to predict the secondary structure and φ dihedral, and filtering FFNN intervening successively to transform the predictions into new values. Hirst group upgraded DESTRUCT into DISSPred that relied on support vector machine (SVM) and obtained better performance ^[54]. SPINE-X by Faraggi et al. in 2012, later replaced by SPOT-1D from the same group, enhanced the accuracy by incorporating physicochemical properties such as hydrophobicity, polarizability, and isoelectric point, among others. This method could also be used for residue solvent accessibility and torsion angle predictions ^[55]^[56]. SPIDER2 launched anticipated multiple 1D-PSAs—secondary structure, solvent accessible surface area (SASA), and torsion angles—all at once with three iterations of deep neural networks ^[57]. Its successor, SPIDER3, improved the performance overall, and now the method predicts four PSAs at once, including contact number with four iterations for the prediction ^[58]. ProteinUnet, published in 2020, yields similar accuracy for secondary structure prediction as SPIDER3-single, but uses half parameters with an 11-fold faster training time ^[59]^[60]. Most servers and methods discussed now have over 84% Q₃ score in their latest versions with deeper neural networks and better algorithms. Considering the explosive advancement in reliability for Q₃ score with DL methods, it might not take too long until the theoretical limit of 88–90% is attained.

One special kind of 1D-PSA targets disordered regions of proteins. Many proteins contain intrinsically disordered regions (IDRs) that are highly flexible. Having multiple structures available, IDRs are involved in assembling, signaling, and many genetic diseases ^[61]. Therefore, this PSA is of particular interest in addition to being a component of full protein structure prediction. IDRs have been predicted using statistical potentials, SVM, or artificial neural networks. IUPred employs a statistical pairwise potential expressed as a 20 × 20 matrix that expresses the general preferences of each amino acid pair in contact ^[62]. The pairwise energy profile is calculated, and disorder probability is estimated accordingly. DISOPRED3 method is formulated on SVM, a supervised machine learning model, to discriminate between ordered and disordered regions ^[63]. DISOPRED3 is trained on PSI-BLAST profile because it outperforms the models trained on single sequences, showing the improvements predicated on evolutionary information. SPOT-Disorder2 offers per-residue disorder prediction based on a deep neural network utilizing LSTM cells ^[64]. Higher accuracy was obtained by upgrading its architecture from a single LSTM topology used in the previous version, SPOT-Disorder, to an ensemble set of hybrid models consisting of residual CNNs with inception paths followed by LSTM layers ^[65].

3.2. 2D Prediction

With the information gained from 1D-PSAs in hand, one might need 2D-PSAs to fully construct the three-dimensional protein structure. Recent endeavors for 2D-PSAs are focused on CM and multi-class CM, both expressing the closeness between residue pairs in a protein. CM takes a binary 2D matrix structure of N × N, where N is the length of the protein sequence, assessing each residue pair as 1 (presence) or 0 (absence) for matrix elements based on the user-defined threshold Euclidean distance (a typical value is ~8 Å between Cα atoms). Multi-class CM is expressed in a 2D matrix, but the matrix elements are quantized in detail, categorized into more than two states. The importance of this CM for protein structure prediction is directly shown in estimations; an early study estimated that one could assemble a structure model within 5 Å RMSD from the native structure if N/4 long-range protein contacts are known, and another study estimated that one contact per twelve residues allows for robust and accurate protein fold modeling ^[66]^[67].

The CM itself definitely provides useful information on the given protein’s spatial organization, but one should note that CMs often contain transitive noise coming from “indirect” correlations between residues. Methods for direct correlation analysis are used to remove this noise such as mutual information (MI), direct coupling analysis (DCA), and protein sparse inverse covariance estimation (PSICOV) ^[68]^[69]^[70]. DCA infers direct co- “evolutionary couplings” among residue pairs in an MSA table to uncover native intra-domain and inter-domain residue–residue contacts in protein families ^[71]^[72].

Many groups have developed CM predictors utilizing multi-stage deep neural networks. The previously introduced Distill server also provides the CM predictor named XX-Stout ^[47]. The developers included contact density profile as an intermediate step using another Distill module named BrownAle ^[73]. Calculating this contact density profile, principal eigenvector significantly increased the performance overall. DNCON by Eickholt and Cheng took advantage of surging GPU developments for training largely boosted ensembles of residue–residue contact predictors ^[74]. MetaPSICOV is another CM predictor known for the first method utilizing co-evolution signals from 1D-PSAs extracted with three different algorithms ^[75]. Then, a two-layer neural network was used to deduce CM. Its successive versions, named MetaPSICOV2 and DeepMetaPSICOV, exist where deeper network architecture and ReLU units are employed. RaptorX-Contact from RaptorX series utilized co-evolution signals to improve the accuracy ^[76]. RaptorX-Contact predicts local structure properties, contact and distance matrix, inter-residue orientation, and tertiary structure of a protein using an ultra-deep convolutional residual neural network from primary sequence or a multiple sequence alignment. DNCON2 is implemented with six CNNs and applied co-evolution signal from 1D PSAs. This method predicts CM with various distance thresholds of 6, 7.5, 8, 8.5, and 10 Å, and then refines them to leave with only 8 Å CM with an improved prediction rate ^[77]. TripletRes starts with the collection of MSAs through whole-genome and metagenome sequence databases and then constructs three complimentary co-evolutionary feature matrices (covariance matrix, precision matrix, and pseudolikelihood maximization) to create contact-map models through deep residual convolutional neural network training ^[78]. DeepContact is also a CNN-based approach that discovers co-evolutionary motifs and leverages these patterns to enable accurate inference of contact probabilities ^[79]. The authors argue that the program is useful, particularly when few related sequences are available. DeepCov uses fully convolutional neural networks operating on amino-acid pair frequency or covariance data derived directly from sequence alignments, without using global statistical methods such as sparse inverse covariance or pseudolikelihood estimation ^[80]. In contrast to other software programs that require third-party programs, Pconsc4 is a hassle-free contact prediction tool that does not use any external programs ^[81].

Recently, in 2019, DeepCDPred was developed, which includes a multi-class CM predictor exploiting distance constraint terms ^[82]. The authors used four FFNN-based models to distinguish four classes of contact ranges: 0–8, 8–13, 13–18, and 18–23 Å. AlphaFold from the same year generates the most fine-grained multi-class CM, 64 equal bins distogram (distance histogram) along 2–22 Å, becoming state-of-the-art for the field ^[83]. An architecture of deep 2D dilated convolutional residual network with 220 residual blocks was employed for the distance map prediction in AlphaFold (note that it will be discussed in more detail in the next section). These 2D-PSA developments have benefitted from the growth of affiliated fields, including algorithmic development and advancement of technologies, which is immediately beneficial for precise 3D structure prediction.

References

Liebschner, D.; Afonine, P.V.; Baker, M.L.; Bunkoczi, G.; Chen, V.B.; Croll, T.I.; Hintze, B.; Hung, L.-W.; Jain, S.; McCoy, A.J.; et al. Macromolecular structure determination using X-rays, neutrons and electrons: Recent developments in Phenix. Acta Crystallogr. Sect. D 2019, 75, 861–877.
Bai, X.-C.; McMullan, G.; Scheres, S.H. How cryo-EM is revolutionizing structural biology. Trends Biochem. Sci. 2015, 40, 49–57.
Wüthrich, K. The way to NMR structures of proteins. Nat. Struct. Biol. 2001, 8, 923–925.
Drenth, J. Principles of Protein X-ray Crystallography; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007.
Anfinsen, C.B. Principles that Govern the Folding of Protein Chains. Science 1973, 181, 223–230.
Pauling, L.; Corey, R.B. Configurations of Polypeptide Chains With Favored Orientations Around Single Bonds. Two New Pleated Sheets 1951, 37, 729–740.
Pauling, L.; Corey, R.B.; Branson, H.R. The structure of proteins: Two hydrogen-bonded helical configurations of the polypeptide chain. Proc. Natl. Acad. Sci. USA 1951, 37, 205–211.
Goodwin, S.; McPherson, J.D.; McCombie, W.R. Coming of age: Ten years of next-generation sequencing technologies. Nat. Rev. Genet. 2016, 17, 333.
Cheng, J.; Tegge, A.N.; Baldi, P. Machine Learning Methods for Protein Structure Prediction. IEEE Rev. Biomed. Eng. 2008, 1, 41–49.
Sun, S. Reduced representation model of protein structure prediction: Statistical potential and genetic algorithms. Protein Sci. 1993, 2, 762–785.
Torrisi, M.; Pollastri, G.; Le, Q. Deep learning methods in protein structure prediction. Comput. Struct. Biotechnol. J. 2020, 18, 1301–1310.
Rost, B.; Sander, C. Combining evolutionary information and neural networks to predict protein secondary structure. Proteins Struct. Funct. Bioinform. 1994, 19, 55–72.
Kuhlman, B.; Bradley, P. Advances in protein structure prediction and design. Nat. Rev. Mol. Cell Biol. 2019, 20, 681–697.
Owens, J.D.; Houston, M.; Luebke, D.; Green, S.; Stone, J.E.; Phillips, J.C. GPU computing. Proc. IEEE 2008, 96, 879–899.
Wilkins, A.D.; Bachman, B.J.; Erdin, S.; Lichtarge, O. The use of evolutionary patterns in protein annotation. Curr. Opin. Struct. Biol. 2012, 22, 316–325.
Floudas, C.; Fung, H.; McAllister, S.; Mönnigmann, M.; Rajgaria, R. Advances in protein structure prediction and de novo protein design: A review. Chem. Eng. Sci. 2006, 61, 966–988.
Moult, J. A decade of CASP: Progress, bottlenecks and prognosis in protein structure prediction. Curr. Opin. Struct. Biol. 2005, 15, 285–289.
Moult, J.; Fidelis, K.; Kryshtafovych, A.; Schwede, T.; Tramontano, A. Critical assessment of methods of protein structure prediction (CASP)—Round XII. Proteins Struct. Funct. Bioinform. 2018, 86, 7–15.
Kryshtafovych, A.; Schwede, T.; Topf, M.; Fidelis, K.; Moult, J. Critical assessment of methods of protein structure prediction (CASP)-Round XIII. Proteins 2019, 87, 1011–1020.
Sun, T.; Zhou, B.; Lai, L.; Pei, J. Sequence-based prediction of protein protein interaction using a deep-learning algorithm. BMC Bioinform. 2017, 18, 1–8.
Wen, M.; Zhang, Z.; Niu, S.; Sha, H.; Yang, R.; Yun, Y.; Lu, H. Deep-learning-based drug–target interaction prediction. J. Proteome Res. 2017, 16, 1401–1409.
Kabsch, W.; Sander, C. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 1983, 22, 2577–2637.
Rodionov, M.A.; Blundell, T.L. Sequence and structure conservation in a protein core. Proteins Struct. Funct. Bioinform. 1998, 33, 358–366.
Sadowski, M.I.; Jones, D.T. The sequence–structure relationship and protein function prediction. Curr. Opin. Struct. Biol. 2009, 19, 357–362.
Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117.
Werbos, P.J. Backpropagation through time: What it does and how to do it. Proc. IEEE 1990, 78, 1550–1560.
Hochreiter, S.; Bengio, Y.; Frasconi, P.; Schmidhuber, J. Gradient flow in recurrent nets: The difficulty of learning long-term dependencies. In A Field Guide to Dynamical Recurrent Neural Networks; IEEE Press: Hoboken, NJ, USA, 2001.
Minai, A.A.; Williams, R.D. Perturbation response in feedforward networks. Neural Netw. 1994, 7, 783–796.
Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A. Inception-v4, Inception-Resnet and the Impact of Residual Connections on Learning. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017.
Hu, Y.; Huber, A.; Anumula, J.; Liu, S.-C. Overcoming the vanishing gradient problem in plain recurrent networks. arXiv 2018, arXiv:1801.06105.
Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal. Process. 1997, 45, 2673–2681.
Baldi, P.; Brunak, S.; Frasconi, P.; Soda, G.; Pollastri, G. Exploiting the past and the future in protein secondary structure prediction. Bioinformatics 1999, 15, 937–946.
Di Lena, P.; Nagata, K.; Baldi, P. Deep architectures for protein contact map prediction. Bioinformatics 2012, 28, 2449–2457.
Pérez-Ortiz, J.A.; Gers, F.A.; Eck, D.; Schmidhuber, J. Kalman filters improve LSTM network performance in problems unsolvable by traditional recurrent nets. Neural Netw. 2003, 16, 241–250.
LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Comput. 1989, 1, 541–551.
Yin, W.; Kann, K.; Yu, M.; Schütze, H. Comparative study of CNN and RNN for natural language processing. arXiv 2017, arXiv:1702.01923.
Hanson, J.; Paliwal, K.; Litfin, T.; Yang, Y.; Zhou, Y. Accurate prediction of protein contact maps by coupling residual two-dimensional bidirectional long short-term memory with convolutional neural networks. Bioinformatics 2018, 34, 4039–4045.
Gligorijevic, V.; Renfrew, P.D.; Kosciolek, T.; Leman, J.K.; Berenberg, D.; Vatanen, T.; Chandler, C.; Taylor, B.C.; Fisk, I.M.; Vlamakis, H. Structure-based function prediction using graph convolutional networks. bioRxiv 2020.
Torrisi, M.; Kaleel, M.; Pollastri, G. Deeper profiles and cascaded recurrent and convolutional neural networks for state-of-the-art protein secondary structure prediction. Sci. Rep. 2019, 9, 1–12.
Zhang, Y.; Qiao, S.; Ji, S.; Li, Y. DeepSite: Bidirectional LSTM and CNN models for predicting DNA–protein binding. Int. J. Mach. Learn. Cybern. 2020, 11, 841–851.
Yang, Y.; Gao, J.; Wang, J.; Heffernan, R.; Hanson, J.; Paliwal, K.; Zhou, Y. Sixty-five years of the long march in protein secondary structure prediction: The final stretch? Brief. Bioinform. 2018, 19, 482–494.
Cuff, J.A.; Clamp, M.E.; Siddiqui, A.S.; Finlay, M.; Barton, G.J. JPred: A consensus secondary structure prediction server. Bioinformatics 1998, 14, 892–893.
Cuff, J.A.; Barton, G.J. Application of multiple sequence alignment profiles to improve protein secondary structure prediction. Proteins Struct. Funct. Bioinform. 2000, 40, 502–511.
McGuffin, L.J.; Bryson, K.; Jones, D.T. The PSIPRED protein structure prediction server. Bioinformatics 2000, 16, 404–405.
Altschul, S.F.; Madden, T.L.; Schäffer, A.A.; Zhang, J.; Zhang, Z.; Miller, W.; Lipman, D.J. Gapped BLAST and PSI-BLAST: A new generation of protein database search programs. Nucleic Acids Res. 1997, 25, 3389–3402.
Magnan, C.N.; Baldi, P. SSpro/ACCpro 5: Almost perfect prediction of protein secondary structure and relative solvent accessibility using profiles, machine learning and structural similarity. Bioinformatics 2014, 30, 2592–2597.
Bau, D.; Martin, A.J.; Mooney, C.; Vullo, A.; Walsh, I.; Pollastri, G. Distill: A suite of web servers for the prediction of one-, two- and three-dimensional structural features of proteins. BMC Bioinform. 2006, 7, 402.
Torrisi, M.; Kaleel, M.; Pollastri, G. Porter 5: Fast, state-of-the-art ab initio prediction of protein secondary structure in 3 and 8 classes. bioRxiv 2018.
Remmert, M.; Biegert, A.; Hauser, A.; Söding, J. HHblits: Lightning-fast iterative protein sequence searching by HMM-HMM alignment. Nat. Methods 2012, 9, 173–175.
Mooney, C.; Vullo, A.; Pollastri, G. Protein structural motif prediction in multidimensional ø-ψ space leads to improved secondary structure prediction. J. Comput. Biol. 2006, 13, 1489–1502.
Kaleel, M.; Torrisi, M.; Mooney, C.; Pollastri, G. PaleAle 5.0: Prediction of protein relative solvent accessibility by deep learning. Amino Acids 2019, 51, 1289–1296.
Klausen, M.S.; Jespersen, M.C.; Nielsen, H.; Jensen, K.K.; Jurtz, V.I.; Sønderby, C.K.; Sommer, M.O.A.; Winther, O.; Nielsen, M.; Petersen, B. NetSurfP-2.0: Improved prediction of protein structural features by integrated deep learning. Proteins Struct. Funct. Bioinform. 2019, 87, 520–527.
Wood, M.J.; Hirst, J.D. Protein secondary structure prediction with dihedral angles. PROTEINS Struct. Funct. Bioinform. 2005, 59, 476–481.
Kountouris, P.; Hirst, J.D. Prediction of backbone dihedral angles and protein secondary structure using support vector machines. BMC Bioinform. 2009, 10, 1–14.
Faraggi, E.; Zhang, T.; Yang, Y.; Kurgan, L.; Zhou, Y. SPINE X: Improving protein secondary structure prediction by multistep learning coupled with prediction of solvent accessible surface area and backbone torsion angles. J. Comput. Chem. 2012, 33, 259–267.
Hanson, J.; Paliwal, K.; Litfin, T.; Yang, Y.; Zhou, Y. Improving prediction of protein secondary structure, backbone angles, solvent accessibility and contact numbers by using predicted contact maps and an ensemble of recurrent and residual convolutional neural networks. Bioinformatics 2019, 35, 2403–2410.
Yang, Y.; Heffernan, R.; Paliwal, K.; Lyons, J.; Dehzangi, A.; Sharma, A.; Wang, J.; Sattar, A.; Zhou, Y. Spider2: A package to predict secondary structure, accessible surface area, and main-chain torsional angles by deep neural networks. In Prediction of Protein Secondary Structure; Springer: Berlin/Heidelberg, Germany, 2017; pp. 55–63.
Heffernan, R.; Yang, Y.; Paliwal, K.; Zhou, Y. Capturing non-local interactions by long short-term memory bidirectional recurrent neural networks for improving prediction of protein secondary structure, backbone angles, contact numbers and solvent accessibility. Bioinformatics 2017, 33, 2842–2849.
Kotowski, K.; Smolarczyk, T.; Roterman-Konieczna, I.; Stapor, K. ProteinUnet—An efficient alternative to SPIDER3-single for sequence-based prediction of protein secondary structures. J. Comput. Chem. 2021, 42, 50–59.
Heffernan, R.; Paliwal, K.; Lyons, J.; Singh, J.; Yang, Y.; Zhou, Y. Single-sequence-based prediction of protein secondary structures and solvent accessibility by deep whole-sequence learning. J. Comput. Chem. 2018, 39, 2210–2216.
Dunker, A.K.; Lawson, J.D.; Brown, C.J.; Williams, R.M.; Romero, P.; Oh, J.S.; Oldfield, C.J.; Campen, A.M.; Ratliff, C.M.; Hipps, K.W. Intrinsically disordered protein. J. Mol. Graph. Model. 2001, 19, 26–59.
Dosztányi, Z. Prediction of protein disorder based on IUPred. Protein Sci. 2018, 27, 331–340.
Jones, D.T.; Cozzetto, D. DISOPRED3: Precise disordered region predictions with annotated protein-binding activity. Bioinformatics 2015, 31, 857–863.
Hanson, J.; Paliwal, K.K.; Litfin, T.; Zhou, Y. SPOT-Disorder2: Improved Protein Intrinsic Disorder Prediction by Ensembled Deep Learning. Genom. Proteom. Bioinform. 2019, 17, 645–656.
Hanson, J.; Yang, Y.; Paliwal, K.; Zhou, Y. Improving protein disorder prediction by deep bidirectional long short-term memory recurrent neural networks. Bioinformatics 2017, 33, 685–692.
Aszodi, A.; Gradwell, M.; Taylor, W. Global fold determination from a small number of distance restraints. J. Mol. Biol. 1995, 251, 308–326.
Kim, D.E.; DiMaio, F.; Yu-Ruei Wang, R.; Song, Y.; Baker, D. One contact for every twelve residues allows robust and accurate topology-level protein structure modeling. Proteins Struct. Funct. Bioinform. 2014, 82, 208–218.
Bitbol, A.-F. Inferring interaction partners from protein sequences using mutual information. PLoS Comput. Biol. 2018, 14, e1006401.
Morcos, F.; Pagnani, A.; Lunt, B.; Bertolino, A.; Marks, D.S.; Sander, C.; Zecchina, R.; Onuchic, J.N.; Hwa, T.; Weigt, M. Direct-coupling analysis of residue coevolution captures native contacts across many protein families. Proc. Natl. Acad. Sci. USA 2011, 108, E1293–E1301.
Jones, D.T.; Buchan, D.W.; Cozzetto, D.; Pontil, M. PSICOV: Precise structural contact prediction using sparse inverse covariance estimation on large multiple sequence alignments. Bioinformatics 2012, 28, 184–190.
Edgar, R.C.; Batzoglou, S. Multiple sequence alignment. Curr. Opin. Struct. Biol. 2006, 16, 368–373.
Dos Santos, R.N.; Morcos, F.; Jana, B.; Andricopulo, A.D.; Onuchic, J.N. Dimeric interactions and complex formation using direct coevolutionary couplings. Sci. Rep. 2015, 5, 1–10.
Walsh, I.; Bau, D.; Martin, A.J.; Mooney, C.; Vullo, A.; Pollastri, G. Ab initio and template-based prediction of multi-class distance maps by two-dimensional recursive neural networks. BMC Struct Biol. 2009, 9, 5.
Eickholt, J.; Cheng, J.L. A study and benchmark of DNcon: A method for protein residue-residue contact prediction using deep networks. BMC Bioinform. 2013, 14, 1–10.
Jones, D.T.; Singh, T.; Kosciolek, T.; Tetchner, S. MetaPSICOV: Combining coevolution methods for accurate prediction of contacts and long range hydrogen bonding in proteins. Bioinformatics 2015, 31, 999–1006.
Wang, S.; Sun, S.; Li, Z.; Zhang, R.; Xu, J. Accurate De Novo Prediction of Protein Contact Map by Ultra-Deep Learning Model. PLoS Comput. Biol. 2017, 13, e1005324.
Adhikari, B.; Hou, J.; Cheng, J.L. DNCON2: Improved protein contact prediction using two-level deep convolutional neural networks. Bioinformatics 2018, 34, 1466–1472.
Li, Y.; Zhang, C.X.; Bell, E.W.; Zheng, W.; Zhou, X.G.; Yu, D.J.; Zhang, Y.; Kolodny, R. Deducing high-accuracy protein contact-maps from a triplet of coevolutionary matrices through deep residual convolutional networks. PLoS Comput. Biol. 2021, 17, e1008865.
Liu, Y.; Palmedo, P.; Ye, Q.; Berger, B.; Peng, J. Enhancing Evolutionary Couplings with Deep Convolutional Neural Networks. Cell Syst. 2018, 6, 65–74.e3.
Jones, D.T.; Kandathil, S.M. High precision in protein contact prediction using fully convolutional neural networks and minimal sequence features. Bioinformatics 2018, 34, 3308–3315.
Michel, M.; Menendez Hurtado, D.; Elofsson, A. PconsC4: Fast, accurate and hassle-free contact predictions. Bioinformatics 2019, 35, 2677–2679.
Ji, S.; Oruc, T.; Mead, L.; Rehman, M.F.; Thomas, C.M.; Butterworth, S.; Winn, P.J. DeepCDpred: Inter-residue distance and contact prediction for improved prediction of protein structure. PLoS ONE 2019, 14, e0205214.
Senior, A.W.; Evans, R.; Jumper, J.; Kirkpatrick, J.; Sifre, L.; Green, T.; Qin, C.; Zidek, A.; Nelson, A.W.R.; Bridgland, A.; et al. Improved protein structure prediction using potentials from deep learning. Nature 2020, 577, 706–710.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Cell Biology

Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Sun Choi

View Times: 555

Update Date: 24 Jun 2021

Table of Contents

Video Upload Options

Confirm