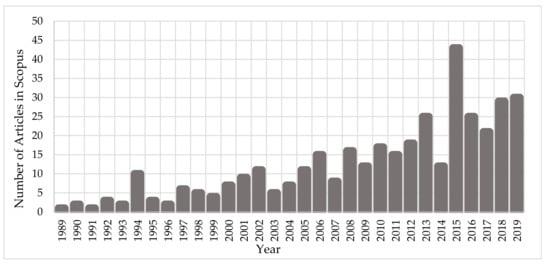
Monte Carlo techniques take advantage of random number generators and computers to simulate complex systems that are not easy to approach in an analytical way. Monte Carlo methods originate from innovative work by Ulam, von Neumann, Metropolis and Fermi in the 1930s and 1940s
[12][13], and are described nicely in Andrieu et al.
[14]. At later stages, MC techniques were used by Eckhardt
[15] and since then they have been applied in many disciplines. They are used in board games, weather forecasting, electrical and telecommunication engineering, quantum physics, and computational biology
[16]. In medical physics, they are used to simulate a range of medical applications that exploit IR, for imaging purposes or for dosimetry applications on the macro- and nano-scale
[17].
Pioneers to MC simulations of DNA energy deposition and strand breaks were Paretzke H.G., Goodhead D.T., Nikjoo H. and Tomita H. In 1989, Nikjoo et al.
[19] published a study (based on
[20]) where they used virtual cylindrical geometrical models to imitate biological models of DNA segments, nucleosomes, and chromatin fibers. To determine the energy deposition in a target volume by ultra-soft X-rays they used the already published, in 1988, mathematical model for track structure analysis by Goodhead et al.
[21]. Tomita et al.
[22] went a step further and used monoenergetic electrons and new DNA structure models (one turn of double-strand DNA, nucleosome, solenoid) to study physical and chemical stages of the radiation interaction. They studied both direct and indirect effects of radiation on the DNA.
2.1. Particle Track Structure Codes
Monte Carlo track structure (MCTS) codes are widely used for simulating the transportation of ionizing particles in biological matter at small scales (nm-μm). Thus, they offer a valuable theoretical tool for mechanistic radiation effect studies, especially in quantifying DNA damage under different radiation qualities, which still presents a major challenge in radiobiology research
[23]. This is not possible with most general-purpose MC radiation transport codes such as MCNP
[24], EGS
[25], FLUKA
[26], PENELOPE
[27], and PHITS
[28], which are widely used for dosimetry at the tissue and organ level (~mm-cm scale). The limitation of these codes stems from the use of so-called condensed-history physics models
[29]. The essence of these models is the grouping of a large number of interactions along artificial steps, which limits their resolution to about 10–100 μm (at best), and prohibits their application at low energies (below about 1–10 keV)
[30].
To reach a spatial resolution at the DNA level, it is necessary to adopt a more detailed description of particle transport, as shown in . This is achieved by simulating all elastic and inelastic collisions one-by-one, until all particles slow down to thermalization energies or, in practice, the ionizing threshold of the medium (which is in around 10 eV for tissue-like materials). The aim is to generate a three-dimensional map of the radiation track based on the spatial distribution of energy-transfer points in the medium
[31]. This functionality has provided a unique theoretical tool for investigating differences between sparse (or low linear energy transfer (LET)) and dense (or high-LET) ionization radiations at the nanometer level, which is not possible by other means
[32]. MCTS codes have been the workhorse of theoretical microdosimetry, enabling systematic calculations of lineal energy spectra (the stochastic analog of LET), proximity functions, ionization cluster distributions, etc., which are used for explaining and predicting the quality factor or the relative biological effectiveness of different ionizing radiations
[33][34][35][36][37][38][39]. In addition, quantitative estimates of the early “direct” DNA damage can be obtained by combining the spatial distribution of energy-transfer points (above a certain threshold) with the geometric structure of DNA
[40][41][42][43][44][45]. The main drawback of MCTS codes is that they are computer intensive and require much more detailed physics models than currently available ones
[46]. In particular, track-structure models for low-energy transport must strongly rely on theory since experimental data are scarce, and they are highly material-specific which limits their application range
[47]. Thus, MCTS simulations are usually application-specific and are developed for a single media, most commonly water.
Figure 2. Particle transport example. (a) Track structure of an electron (10 KeV) in water as simulated in Geant4-DNA. The red line, which starts from the bottom right edge, is the route followed by the primary electron, while in yellow the interactions with the water medium are presented. The red branches that are separated from the main route represent secondary electrons. (b) Schematic representation of the way that energy is deposited on DNA molecules. This is a stylish representation, which has the aim of helping the reader understand the way that the superposition of energy deposition in water is transformed to single or double strand breaks. The blue edges imitate DNA bases.
MCTS codes for water have been used for over 40 years in radiation biophysics, and more than a dozen such codes have been reported in the literature
[23], with the most widely used being NOREC
[48], PARTRAC
[20], KURBUC
[49], and RITRACKS
[50]. Although most of the early MCTS codes were limited to electrons, nowadays most MCTS codes can also simulate more heavily charged particles like protons, alphas, and some ions. NOREC (NIST-modified Oak Ridge Electron Code) is an upgraded version of the OREC code developed in the ‘70s at the Oak Ridge National Laboratory (ORNL) by Ritchie and co-workers
[51]. OREC was the first MCTS code to implement a realistic physics model of the liquid-phase of water based on an empirical dielectric response function deduced from optical measurements at ORNL
[52]. This major achievement allowed the calculation of ionization and excitation cross sections for condensed-phase water from first principles. OREC was also one of the first MCTS codes to extend the simulations to the chemical stage with a detailed radiolysis model that was extensively benchmarked against experimental data
[53]. In the early 2000s, following an upgrade of the elastic scattering model based on NIST’s ELAST database, OREC was renamed to NOREC
[48]. NOREC can simulate full slowing-down electron tracks over the energy range from 7.4 eV to 1 MeV. PARTRAC (PARticle TRACks) is an evolution of the MOCA (MOnte-CArlo) code developed in the 1970s by Paretzke and co-workers at the National Research Center for Environment and Health (GSF) of Germany. MOCA was one of the first MCTS codes for electron transport in biological matter represented by unit-density gaseous water
[20]. PARTRAC has evolved to a comprehensive MCTS code that extends to the chemical and biological stage, including multi-scale models for the structure of the whole genomic DNA with atomic resolution, which are supplemented with DNA damage and repair models
[54]. It has also adopted more realistic physics models for the biological medium based on the empirical dielectric response function of liquid water developed by Dingfelder and co-workers
[55]. PARTRAC can transport electrons (10 eV–10 MeV), protons (1 keV–1 GeV), alpha-particles (1 keV–1 GeV), and light ions (from <1 MeV/u up to 1 GeV/u)
[56], and it can also take into account water radiolysis, DNA repair and chromosomal aberrations
[57][58][59]. KURBUC (Kyushu University and Radiation Biophysics Unit Code) was initially developed at the Medical Research Council (MRC) of UK in the early 1990s by Nikjoo and co-workers using mostly empirical and parameterized physics models for electron transport in unit-density gaseous water mediums in the energy range from 10 eV to 10 MeV
[60]. It was later extended to protons (1 keV–1 MeV), alpha particles (1 keV/u–2 MeV/u), neutrons (thermal to 100 MeV), and carbon ions (1 keV/u–10 MeV/u). In its latest version, KURBUCliq
[49], a more realistic physics model for biological matter, has been implemented using the dielectric response function developed by Emfietzoglou, Cucinotta, and Nikjoo (known as the ECN model)
[61] which is based on the latest experimental data for liquid water. KURBUCliq can also perform simulations of the chemical and biological stage including sophisticated mathematical models of DNA damage and repair pathways along with atomistic DNA structure models
[62][63][64]. RITRACKS (Relativistic Ion TRACKS) is a NASA-funded MCTS code that extends the transport of ionizing particles in unit-density gaseous water mediums up to the very highest energies (100 MeV for electrons and 10 GeV/u for ions), which are of interest to space radiation protection. Molecular cross sections specific to the DNA bases (in the gas phase) are also available towards a more realistic approximation of direct ionizations in DNA. A distinct feature is the implementation of time-dependent track effects in order to simulate dose-rate effects. It also includes modeling of water radiolysis and simple DNA structures for radiation damage studies
[65]. Recently, the RITRACKS code has been used and the results advocate for the hypothesis that not only a single particle may induce many non-DSB clustered damages, but also that there may be a large number of them in a chromatin fiber
[66]. The TRAX code performs simulations for track-structure applications in various media
[67]. MC4 performs simulations down to very low energies, including models for gaseous and liquid water, and is known for its upgraded models for the liquid phase
[68][69]. PHITS has been developed to simulate the track structure of electrons in liquid water in a wide incident energy spectrum from 1 meV to 1 MeV
[70].
The aforementioned MCTS codes are not publicly available. Therefore, in recent years, there have been efforts to implement track-structure models into some general-purpose MC codes to enable simulations at both the macro and microscopic scale. The most notable examples are the Monte Carlo N-Particle version 6 (MCNP6)
[71], PENELOPE (modification to PENELOPE/penEasy, resulting in the LionTrack code)
[72][73][74], and the Geant4-DNA package of Geant4
[75][76][77]. Apart from MCNP6, which uses a simple interpolation of high-energy atomic models down to the eV energy range, thus neglecting molecular aggregation and condensed-phase effects, the Geant4-DNA and modified PENELOPE/penEasy extensions are based on elaborate physics models specifically developed for liquid water. The code PENELOPE is known for its electron models and extends accurately to low energies, having applications to micro- and nano-dosimetry
[78][79], however, the low-energy modification of the PENELOPE code is not publicly distributed. Therefore, since 2007, Geant4 (release 9.1) is the only open access general-purpose radiation transport MC code offering, through its Geant4-DNA extension, track-structure functionalities in liquid water down to the eV energy range for radiobiological applications at the cellular, sub-cellular, and DNA level
[75][76]. Due to the prominent role of low-energy electrons (called “track-ends”) in radiation-induced DNA damage, a distinct feature of Geant4-DNA is the availability of different physics models for the interaction of low-energy electrons with liquid water
[39][80][81][82]. These models, which adopt either the dielectric response function approach or other hybrid approaches, undergo continuous development and refinement. Recently, track-structure models for gold nanoparticles have also been developed and will be incorporated in the upcoming Geant4-DNA releases
[83][84][85]. It also includes modelling of the chemical stage
[86] and offers various representations of DNA target structures to be used in DNA damage studies
[87][88][89]. Geant4-DNA can transport electrons (7.4 eV–1 MeV), protons (100 eV–100 MeV), alpha particles (1 keV–400 MeV), and ions (0.5 MeV/u–10
6 MeV/u). It is noteworthy that the TOPAS-nBio software
[90], which extends the TOPAS MC code
[91] to the (sub) cellular and DNA scale for radiobiological studies
[92], is based on the Geant4-DNA package.
The aforementioned MCTS codes have great potential to expand the knowledge of mechanisms that are involved in the response of biological matter to IR, but they also have limitations. The limitations vary from the lack of experimental information on the processes involved, which are also under research, up to the broad uncertainty of used parameters or the large fluctuations of parameters that are exploited to describe cell sensitivity. Another obstacle is that not all MCTS codes are benchmarked, especially with respect to nanodosimetric calculations. MCTS codes are very sensitive to the physics cross sections that are used for particle transportation as they are the core of the computation. These cross sections vary depending on how they are produced (analytically, extrapolation, or experimentally) and therefore they introduce a wide uncertainty to the simulation of track structures. This undoubtedly influences the results of MCTS simulations, e.g., the number of interactions within a certain volume, which is very critical when it comes to nanodosimetry (somewhat less for microdosimety). Thus, there is an urgent need for benchmarking MCTS codes with some efforts being done recently
[93]. The computational time of the simulation for a population of cells is also a big concern. MCTS codes are also not capable enough to reliably simulate the very low energy secondary electrons below about 10 eV, which are considered as potential lethal sources for the cell since they can induce harmful clustered lesions in the DNA
[94][95].
2.2. Monte Carlo Techniques for Radiobiological Modelling
Currently, there are two methods used to estimate DNA damage. The first method is to estimate potential DSBs by superimposing DNA geometry to the radiation track structure
[42][44][96][97][98]. The other method is to use clustering algorithms based on probabilistic models to estimate DSB yield
[99][100][101]. The first method is more direct way to estimate DNA damage accurately, but it is also a time-consuming procedure. The second method can also calculate with reasonable accuracy the DNA DSB, and it reduces the computational time. Monte Carlo Damage Simulation (MCDS)
[102][103][104] and DBSCAN
[105] are two platforms that can be used for such a purpose. A study has already been done to compare DBSCAN with Geant4-DNA simulation results by Lampe et al.
[106][107].
The RADAMOL
[108][109] toolbox includes the simulation of chemical and physico-chemical stages produced when ionizing particles interact with water. To simulate scavengeable and unscavengeable DNA damage, it also includes RADACK and DIRADACK. PARTRAC
[55] is focused on radiation biology and can simulate both physics and chemistry interactions produced by the irradiation of biological materials. PARTRAC also includes mathematical models of biology to study the procedure of recombination of DNA segments after irradiation
[110] and has integrated information on DNA and chromatin structure over multiple levels and the susceptibility of DNA damage, as well as enzymatic reactions that aim to restore the integrity of the cellular DNA. PARTRAC, in its follow-up chemistry component, can account for inter-track effects
[111], a feature that Geant4-DNA also implanted in its code. Geant4-DNA has been often compared with PARTRAC, for validation purposes
[112][113], while PARTRAC publications influenced the design of Geant4-DNA code.
A recent addition on simulating radiation chemistry and track structures at the subcellular scale is the MPEXS-DNA, GPU-based Monte Carlo simulator
[114]. MPEXS-DNA uses the speed of GPU processing for the physical, physicochemical, chemical and biological stages of the simulation process of IR interaction with biological matter. It is based on the Geant4-DNA package and can also simulate chemical reactions and the diffusion process for molecular species, and the distribution of molecular species can also be determined. In this study
[114], the authors confirmed that the simulation results, which were obtained using MPEXS-DNA, were consistent with existing experimental and simulation data. Compared with simulations that were performed in Geant4-DNA with a single CPU core, MPEXSDNA performed the same simulations thousands times faster, keeping the accuracy at the same level.
The Monte Carlo Damage Simulation (MCDS)
[102][103] algorithm, as a cell-level model, is a quasi-phenomenological concept used to simulate DNA damage yields (SSBs, DSBs and sites of multiple base damage, average number of lesions per DNA damage cluster, as well as cluster length in base pairs). It is a fast algorithm compared to common track-structure simulations (execution time ranges from seconds to some minutes on a typical PC). It utilizes monoenergetic electrons, protons, α-particles and other charged particles with atomic numbers up to Z = 26 (i.e.,
56Fe), with kinetic energies up to a few GeV
[102][103][104]. It also has the ability to simulate damage induction for random mixtures of charged particles. For photons and neutrons, MCDS can provide the distribution of secondary charged particles produced via the interaction of neutral particles with a target region of interest
[115]. Considering the spectrum of energy used for the particles involved in MCDS, the minimum allowed kinetic energy limit depends on the particle type: e.g., for electrons, damage induction can be simulated from some tens of eV, while for bigger particles the corresponding limit increases with increasing atomic number. This code can also simulate the effects of oxygen on the induction of clustered DNA lesions. Because of the fact that MCDS provides simulations tacitly for both direct and indirect DNA damage mechanisms, it uses an extraneous free radical scavenger (DMSO) and thus imitates diminutions in the total amount of strand breaks and base damages because of the scavenger’s presence
[102]. It must be mentioned at this point that MCDS simulates the so called “initial” levels of DNA damage induced and not the processing or repair.
2.3. DNA Modelling
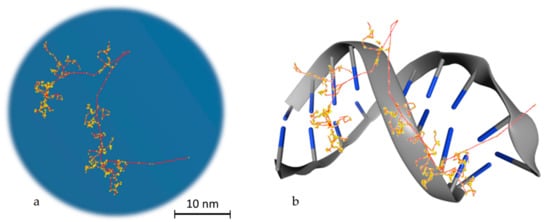
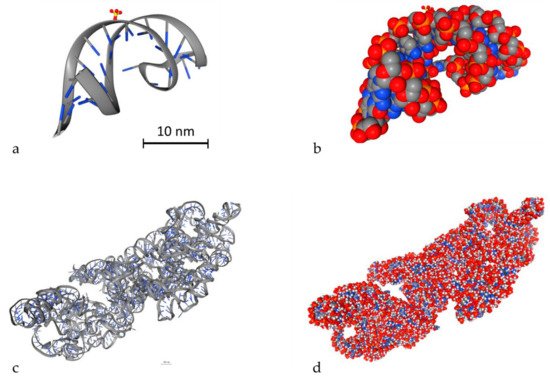
An important parameter to simulate DDR is to model DNA molecules. There are two ways to model DNA molecules. One way is to use simulation techniques and the other one is to use geometry design techniques. There are also fixed DNA geometries that can be downloaded by the Proteins Data Bank (PDB)
[116]. PDB (
http://www.rcsb.org/) is a big database that contains high detailed DNA molecules, but it does not contain every DNA molecule. In Geant4-DNA, there is an example (PDB4DNA
[117]) that includes a model by this database. In , two different DNA molecules that were provided by the PDB database are presented in several styles. The stylish representation has been used to make the reader understand the geometry of the DNA molecule. The “simulation” representation is the one used by the MC simulation algorithms and they represent each different ingredient of the DNA molecule with spheres of different colors. Bases are shown in blue while the backbone is shown in grey and red. The spheres are the space where energy is deposited. The first one is a simple and small molecule (a,b) (linear, with 20 base pairs length), while the second one (c,d) is a more complex DNA molecule (5000 base pairs). Simulation software usually exploits the geometry shown in b,d to calculate energy deposition.
Figure 3. 3D view of two different DNA molecules by the Proteins Data Bank (PDB) database. Scale bars have been added accordingly. Both scale bars represent a distance of 30 nm. (a) Simple small DNA, stylish view, (b) simple small DNA, “simulation” view, (c) complex DNA, stylish view, (d) complex DNA, “simulation” view.
A DNA simulation tool is MacroMoleculeBuilder (MMB)
[118], which has been implemented using the SimTK simulation toolkit
[119]. SimTK provides the user with several simulation tools, including Simbody (
https://simtk.org/projects/simbody/) and Molmodel (
https://simtk.org/projects/molmodel). These algorithms allow the implementation of specified joint constrains using coordinates, which allow the user to control the flexibility of the generated molecule. MMB can simulate the interactions between bases, which are exploited to produce the geometry of any combination of base pairs. An analytical classification of base pairs can be found in the Leontis–Stombaugh–Westhof catalog
[120]. The catalog contains several combinations of force and torque that tend to produce an attachment frame around the first residue’s base, with a body frame on the second residue’s base.
Furthermore, Howell et al. proposed a simulation algorithm for the modelling of B-DNA
[121]. They exploited coarse-grained (CG) simulations based on the bead-rod model reported by Wang et al.
[122] that originated in the wormlike chain model
[123]. In this model, the DNA molecules are designed using N beads connected by N−1 inextensible rods of length l, with a total length L. The final model has a length of L = (N−1)l. For energy compensation, the model employs a bending penalty between adjacent beads and an excluded volume repulsion between beads. This algorithm can generate several different structures where the only common thing is their ingredients. This model can only support homogeneous DNA bending and cannot be extended to more complex configurations that include DNA kinking and stretching
[124].
Cumberworth et al.
[125] introduced several sampling methods that create a model which can simulate computationally feasible DNA origami self-assembly. The model can contain structural parameters relevant to the process of construction. There are several different methods, using different sets of parameters, to produce similar designs. For large-scale systems, the results can be highly different as there is a connection between the variables of the origami design.
The above-described DNA simulation models have not yet been used in MC simulations. Recently, DnaFabric
[126] has been presented and used in Geant4-DNA. The purpose of DnaFabric is to generate, edit, display, and export complex DNA geometrical models. It is based on a hierarchical geometry description designed to adapt to optimization techniques and adaptable level of detail (LODs).