1000/1000
Hot
Most Recent

Low-Cost Microwave Doppler Radar Systems is an alternative noncontact solution for structural condition monitoring. In addition, by leveraging their capability of providing the target velocity information, the radar-based remote monitoring of complex rotating structures can also be accomplished. Modern radar systems are compact, able to be easily integrated in sensor networks, and can deliver high accuracy measurements.
Radars have been employed since 1940s [1]. In the past, they were mainly used in military, navigation, and meteorology due to high costs and bulky sizes. Thanks to the fast and significant advancements in the semiconductor industry, radars are being miniaturized and assembled on printed circuit boards (PCB) or even integrated into a single chip with antenna-on-chip/antenna-in-package technologies [2][3][4][5]. In the last decades, portable short-range radars have been investigated for human and animal vital signs, remote voice recording, gait analysis, fall detection, gesture characterization, occupancy sensing, and security applications [6][7][8][9][10][11][12][13][14][15][16][17][18][19]. Biomedical Doppler radars have also been employed in cancer radiotherapy for respiratory gating and tumor tracking for motion-adaptive radiotherapy [20][21][22]. In addition, short-range radars can be used to provide time-frequency analysis of microwave signals backscattered by rotating structures such as wind turbines [23][24][25][26][27][28].
Structural health monitoring (SHM) is the process of continuous observation of a structure or mechanical system using one or multiple sensors to provide information about its true capacity, which is altered by age and/or accidental damage. By sensing low-frequency small-amplitude mechanical vibration or deflection of structures, radars may also be successfully employed for the SHM of infrastructures. As the aging of worldwide infrastructures raises concerns and the appearance of new structures forces researchers and engineers to look for alternative solutions for SHM measurements and the improvement of existing ones, private industries and government organizations demand technologies that are able to detect structural damage at the earliest possible time to avoid life-threatening situations and economical losses.
Several technologies targeting SHM have been proposed in the past decades. Accelerometers are commonly used to evaluate the infrastructure health condition and to extract damage-sensitive features because they are relatively cost-effective and can be readily instrumented. Nevertheless, the double integration of the acceleration data makes displacement measurements susceptible to integral drift errors [29]. Strain sensors, laser displacement sensors, and vision-based systems are also representatives of nonintrusive solutions for SHM applications. However, these sensors present practical limitations. The measurements retrieved by strain gauges are sensitive to temperature variations, and they may need periodical calibration. Laser displacement sensors are sensitive to the measurement range and the structure’s surface condition. Vision-based systems demand large data storage, high computational load for image recognition and are not robust against ambient light.
On the other hand, radars can make use of different types of waveforms for the targeted application. Continuous-wave (CW) radars have simple architecture, allowing for easier integration and lower power consumption, which makes them appealing for portable applications. In a basic CW radar system, the radio frequency (RF) wave is radiated, and an echo returns after being backscattered by a surrounding target. If the target is moving, a shift in the received radar signal due to the Doppler effect is observed. The target’s range can only be assessed by modulated CW radars. Modulated CW radars such as frequency-modulated continuous-wave (FMCW) radars and stepped-frequency continuous-wave (SFCW) radars are popular candidates for applications that require range and/or Doppler information. In contrast, unmodulated CW radars, widely known as Doppler radars, do not have range discrimination capability. Nonetheless, Doppler radars can measure time-varying small-amplitude periodical motion with high accuracy [2].
The most common radars employed on structural condition monitoring are the ground-based interferometric (GBI) radars. Their use for SHM applications has a relatively long history. The inspiration for the utilization of GBI radars on the monitoring of structures such as building or bridges came from the success of spaceborne synthetic aperture radar (SAR) radar systems, which operate at high orbits and detect ground changes based on the phase information of radar images [30][31]. During onsite testing, these sensors are typically mounted on a tripod and pointed towards bridges, landslides, towers, and dams [32][33][34][35][36][37][38][39][40][41][42][43][44][45][46][47][48][49][50][51][52][53][54][55]. The main difference between GBIR and other portable radar sensors is their relatively large detection range due to the use of bulky, high directivity antennas and waveguide-based components [38]. By transmitting and receiving electromagnetic waves at microwave frequencies, they can remotely detect small displacements of targets using the interferometric technique, and they are also able to distinguish the real displacement of targets of interest from clutter since the vast majority of GBI radar systems employs stepped-frequency continuous-wave (SFCW) or frequency-modulated continuous-wave (FMCW) radar sensors. These systems can operate without any angular resolution or with angular resolution obtained through the rotation of the radar or the movement of the radar along a linear mechanical guide. GBI radars are powerful tools on the estimation of vibration parameters of structures with large areas (bridges, mines, buildings). Bridge monitoring using portable GBI radars dates back to the 2000s [32]. The evaluation of the bridge displacement along the radial direction by an SFCW or FMCW radar systems starts by choosing the range bin associated with different parts of the structure. After the selection of the range bin, the displacement of the target is recovered by demodulating the phase variations of the received signal during the detection time. Another important parameter of modulated wave radar is the range resolution, which is a function of the transmitted bandwidth and is the minimum distance to resolve two or more adjacent targets on the same bearing.
Most monostatic radars detect motion along the radial direction, and the movement of real large targets such as buildings or bridges consists of more than one component. To address the challenge of simultaneously measuring displacements along different directions, the most recent work on SHM based on GBI radars proposed a multi-monostatic 17.2-GHz FMCW radar for the remote monitoring of bridges [55]. They employed two different interferometric radars placed at different positions to measure two components of a bridge’s deck motion. The used radar system was a modified version of a multiple-input multiple-output (MIMO) GBI radar (IBIS-FM MIMO by IDS Company) that operated with two pairs of transmitting (Tx) and receiving (Rx) antennas (four possible baseband channels). Only two channels were effectively used to retrieve the displacements at two different positions (23 m and 33 m away from the main radar) on the bridge. RF cables were utilized to connect the second pair of Tx/Rx antennas to the main radar system, allowing for the multi-monostatic radar architecture. The radar operated sequentially in a single channel modality, but the time duration between four acquisitions was relatively short (5–12 ms), especially for SHM applications. The cable loss and the time shifts were compensated by low noise amplifiers and by digital signal processing techniques, respectively. The authors chose the 127-m long Varlungo Bridge in Firenze, Italy, to conduct the full-scale experiments. The vehicular traffic provoked the bridge vibration, but a significant change on the displacement was only observed when a truck moved on the bridge. With this strategy, the authors were able to retrieve the displacement vector (y-z plane) and the natural frequencies for the two different radar targets. However, no discussion was made towards modal analysis measurements. In addition, the proposed method relies on choosing an appropriated distance between the main radar and the second pair of Tx/Rx antennas, which must be large enough to allow the evaluation of the vector displacement using the two motion components. The radar had achieved submillimeter accuracy during measurements in a controlled environment with an oscillating corner reflector placed 12.88 m away from the main radar and 7.33 m away from the second pair of antennas. Seismic accelerometer measurements (PCB 393B31 by PCB piezotronics) provided the ground truth.
Doppler radars emit a single-tone microwave signal of frequency ft. The reflected radio-frequency signal is frequency/phase-modulated due to the Doppler effect assuming that the target is moving. The microwave frequency associated with the translational speed v of a point-scatterer target is calculated as fr=ft(1+v/c)/(1-v/c), and can be easily retrieved by spectral analysis. If the target consists of several moving parts, the contributions of various point-scatterers produce micro-Doppler signatures, which can be exploited for the extraction of other parameters not related to the main target’s movement [23]. For example, when one does hand gestures in front of a radar sensor, not only will the Doppler frequencies associated with the hand’s movement be captured, but also the frequencies associated with the movements of other parts of the human body such as the arm and the elbow [17][18].
Assuming that a simple homodyne Doppler radar illuminates a structure comprised of rotating blades, as seen is Figure 1, the reflected signal is phase-modulated by their movement. The returned echoes are mixed with the same transmitted signal by a quadrature-mixer to generate in-phase (I(t)) and quadrature-phase (Q(t)) baseband responses. The analytic form of the amplitude-normalized baseband signal can be cast as sb(t) = I(t) + jQ(t) =![]() , where the time-varying distances between the radar sensor and each of the K scatterers are Rk(t) and K is the number of scatterers. Taking into account that the blade’s surface backscatters significant radar signals in the perpendicular direction, the distance between each scatterer and the radar makes the total received signals be coherently added. Therefore, its micro-Doppler signatures will have the form of flashes in the time-Doppler maps [28].
, where the time-varying distances between the radar sensor and each of the K scatterers are Rk(t) and K is the number of scatterers. Taking into account that the blade’s surface backscatters significant radar signals in the perpendicular direction, the distance between each scatterer and the radar makes the total received signals be coherently added. Therefore, its micro-Doppler signatures will have the form of flashes in the time-Doppler maps [28].
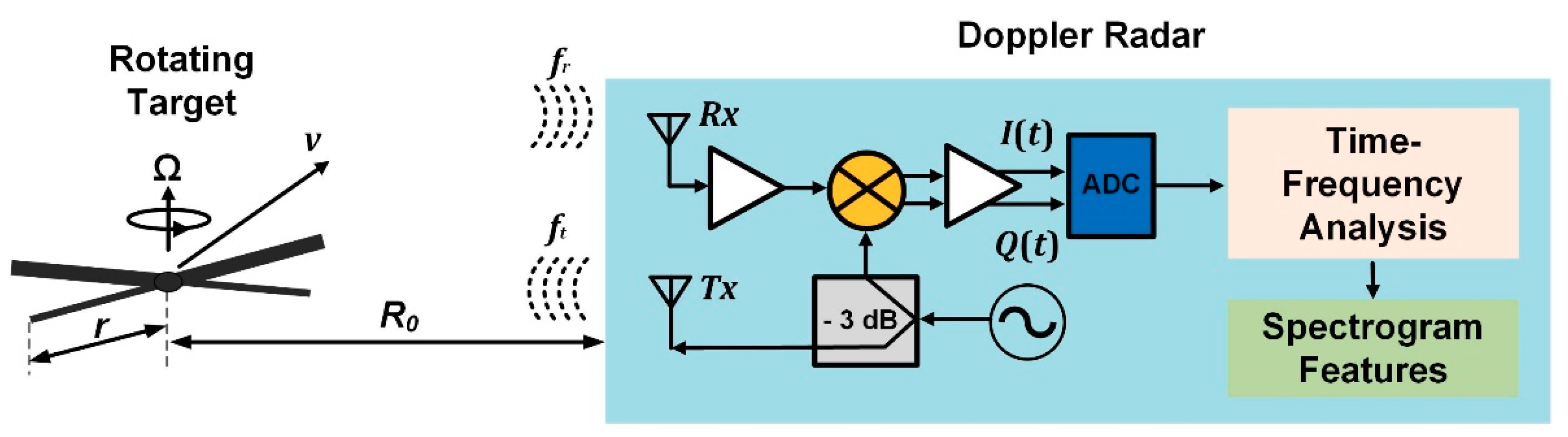
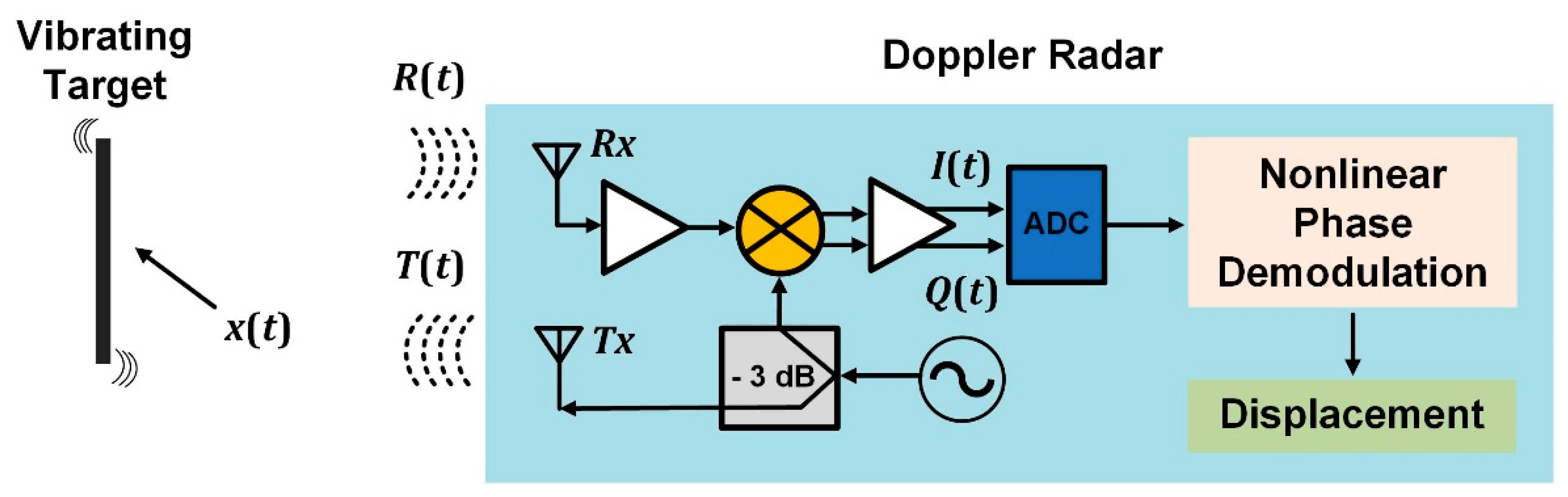 Figure 2. Block diagram for the SHM based on low-cost Doppler radars through remote vibration monitoring.
Figure 2. Block diagram for the SHM based on low-cost Doppler radars through remote vibration monitoring.Powered by the advancements of semiconductor technologies, Doppler radar can be miniaturized, which led to vast practical implementations in the civilian world. The recent technical advancements on digital signal processing pushed the technology further into smart integration with embedded systems. In addition, the potential costs of Doppler radar sensors after CMOS integration and mass production would possibly make them even more appealing than other noncontact approaches for SHM such as camera systems and laser vibrometers. Beamforming technology can also be exploited to address the current issue of measuring only the displacement on the radial direction. Furthermore, by leveraging the compactness of low-cost Doppler radars, radar sensor networks can be deployed. Although the adoption of low-cost, compact radars still lags behind other technologies, SHM researchers and engineers can be optimistic about the promising possibilities for low-cost radars with the rapid dissemination of chipset-based sensors and migration to mm-wave bands.