
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Rafael Lahoz-Beltra | + 1182 word(s) | 1182 | 2020-04-22 12:04:41 | | | |
| 2 | Rafael Lahoz-Beltra | + 1181 word(s) | 1181 | 2020-04-22 13:43:15 | | | | |
| 3 | Rafael Lahoz-Beltra | + 89 word(s) | 1270 | 2020-04-23 10:58:15 | | | | |
| 4 | Rafael Lahoz-Beltra | + 89 word(s) | 1270 | 2020-04-23 11:28:36 | | | | |
| 5 | Rafael Lahoz-Beltra | Meta information modification | 1270 | 2020-05-04 10:32:37 | | | | |
| 6 | Lily Guo | -23 word(s) | 1247 | 2020-10-29 09:41:03 | | | | |
| 7 | Lily Guo | -23 word(s) | 1247 | 2020-10-29 09:42:07 | | | | |
| 8 | Lily Guo | -23 word(s) | 1247 | 2020-10-29 09:42:54 | | | | |
| 9 | Catherine Yang | Meta information modification | 1247 | 2020-11-05 11:17:41 | | |
Video Upload Options
The Gompertz function is a sigmoid curve being a special case of a logistic curve. Although it was originally designed to describe mortality, it is now used in biology. For example, it is useful to describe many phenomena such as the growth of a cancerous tumor confined to an organ without metastasis, the growth of the number of individuals in a population, e.g. prey in a Volterra-Lotka model, the germination of seeds, etc. It also models as the logistic function the growth of a colony of bacteria or in an epidemic the spread of the number of infected people. However, despite its many applications, in many cases the fitting of experimental data to the Gompertz function is not always straightforward. In this article we present a protocol that will be useful when performing the data regression to this curve using the statistical package R.
1. Introduction
One of the issues related to the Gompertz function on which there are many blog and website posts is the fitting of experimental data to this function[1]. The usual method is the non-linear regression technique, which in practice can be easily conducted in R. Nevertheless, the non-linear regression of the Gompertz function is not a trivial matter since we must provide the initial values of three parameters of the equation: a, b and c. The parameter 'a' is an asymptote obtained by doing the limit of the function when x tends to infinity, 'b' is the displacement on the x-axis, and finally 'c' is the growth rate. In the particular case of the logistic curve to give an estimate of the initial value of the function parameter is straightforward because there is only one parameter, whereas he Gompertz function has three parameters. Therefore, when we provide estimates of the initial values of the three parameters, it is very common and disappointing that the statistical software we are using does not give us an answer or, as in the case of R, returns a message of the type 'singular gradient .'. At this point in time, there are many recipes on the Internet that are usually not useful, frustrating the best wishes of the most hard-working student, engineer, professor, or researcher. This means that until we provide a proper initial estimate of the values of a, b and c, the non-linear fitting of the data to the Gompertz curve will not be successful.
In addition, there is an issue that usually is confusing and is the fact that the curve can be presented with different format, that is, with different mathematical expressions:
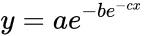
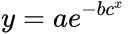
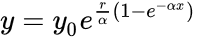
In general, the double-exponential (1) is the favorite expression whereas the expression (2) with a single exponential is usually easier to fit. Finally, expression (3) is limited to biomathematics, and applied mainly in the academic sector. In the latter expression (3), 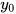
2. A general protocol for fitting data to the Gompertz function
Next, we will explain in a simple way how to succeed when applying R software in the non-linear fitting of the experimental data to the Gompertz curve[2]. In the example, we will use the data from a chinese hamster V79 fibroblast tumor (Marusic et al., 1994). The data file (ChineseHamsterV79.csv) collects in two columns the time (t is x, days) and the volume (y, 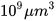
First, we will recreate the best scenario, that is to say the one in which we provide proper estimates of the three parameters of the Gompertz function. We will fit the experimental data to the double exponential (1). In order to achieve this result we will use the Method 1 script, setting the values of the parameters: a = 1.0, b = 13.0, c = 0.09. Once the script is executed under R, we get the results of the fitting, i.e. the function of the Gompertz curve and the Figure showing the experimental data:
Formula: V2 ~ a * exp(-b * exp(-c * V1))
Parameters:
Estimate Std. Error t value Pr(>|t|)
a 7.479960 0.130692 57.23 < 2e-16 ***
b 13.582015 2.378544 5.71 1.04e-06 ***
c 0.126354 0.008496 14.87 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3662 on 42 degrees of freedom
Number of iterations to convergence: 7
Achieved convergence tolerance: 7.875e-06
Secondly, we will simulate the most common situation, i.e. where we do not provide a good estimate of one or more of the function parameters. For example: a = 0.01, b = 6.0, c = 0.02. In this case, R provides the following frustrating output:
Error in nls(V2 ~ a * exp(-b * exp(-c * V1)), start = list(a = 0.01, b = 6, :
singular gradient
> summary(output)
Error in summary(output)
In such a case, how will we solve what is known as 'singular gradient matrix error'? Let's apply Method 2, keeping in mind that the data are fitted to the function (2), that is, to a single exponential function. Note that in this case no prior estimation of the parameters must be given in the R script. Once the script is run we get the function , and therefore the output:
Formula: V2 ~ SSgompertz(V1, Asym, b2, b3)
Parameters:
Estimate Std. Error t value Pr(>|t|)
Asym 7.479966 0.130692 57.23 < 2e-16 ***
b2 13.581893 2.378511 5.71 1.04e-06 ***
b3 0.881303 0.007487 117.71 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3662 on 42 degrees of freedom
Number of iterations to convergence: 0
Achieved convergence tolerance: 1.642e-06
Now, depending on the problem we are working on and our goals, we can choose to keep the function (2) or try to fit the experimental data to (1). If your choice is to try to fit the data to the double exponential (1), note that in (2) the Asym, b2 and b3 parameters match with a, b and c in (1). Therefore, the solution is simple and quick: use in Method 1 the values of Asym, b2 and b3 or their rounded values as estimates of the initial values of a, b and c; verifying, once the script is run in R, how it no longer gets the error 'singular gradient'.
3. Scripts in R
Following, we show the code of the previously used methods. The scripts ran properly under R version 3.5.2 (2018-12-20):
METHOD 1
================================================================
install.packages("data.table")
install.packages("nlme")
library(data.table)
library(nlme)
# Read data
mydata<-read.table("C:/Users/./R/ChineseHamsterV79.csv",header=F)
attach(mydata)
names(mydata)
#Plot figure
plot(V1,V2,pch=4)
#Non-linear regression. METHOD 1 :give initial parameter values
output <-(nls(V2~a*exp(-b*exp(-c*V1)),start = list(a = 1.0, b = 13.0, c = 0.09)))
summary(output)
================================================================
METHOD 2
================================================================
install.packages("data.table")
install.packages("nlme")
library(data.table)
library(nlme)
# Read data
mydata<-read.table("C:/Users/./R/ChineseHamsterV79.csv",header=F)
attach(mydata)
names(mydata)
#Plot figure
plot(V1,V2,pch=4)
#Non-linear regression. METHOD 2 : SSgompertz
output <- nls(V2 ~ SSgompertz(V1, Asym, b2, b3), data=mydata)
summary(output)
plot(V2 ~ V1, data = mydata)
curve(predict(output, newdata = data.frame(V1 = x)), add = TRUE)
================================================================
Gabriel and Galan et al. (2015)[3] describes another but more sophisticated method of setting initial values for the Gompertz function parameters. In this case the symbolic computer program DERIVE was used, and the commercial statistical software STATGRAPHICS was applied to perform the non-linear regression. The paper describes a study on fern spore germination, fitting in some species to the Gompertz function and in others to the logistic function. Consequently, the described method based on R-scripts is much easier to apply and also has the advantage of using non-commercial software.
References
- Marusic, M.; Bajzer, Z.; Freyer, J.P.; Vuk-Pavlovic, S.; Analysis of growth of multicellular tumour spheroids by mathematical models. Cell Proliferation 1994, 27, 74-94.
- Wang, J . Modeling cancer growth with differential equations. Retrieved 2020-4-22
- Gabriel y Galan, J.M.; Prada, C.; Martinez-Calvo, C.; Lahoz-Beltra, R.; A Gompertz regression model for fern spores germination. Anales del Jardin Botanico de Madrid 2015, 72(1), e015.




