Smart Electrical Energy Systems: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Contributor:
Huilian Liao
,
Elizabeth Michalenko
,
Sarat Chandra Vegunta

Energy systems around the world are going through tremendous transformations, mainly driven by carbon footprint reductions and related policy imperatives and low-carbon technological development. These transformations pose unprecedented technical challenges to the energy sector, but they also bring opportunities for energy systems to develop, adapt, and evolve.

  • big data analytics
  • network planning and operation
  • smart grids

1. Introduction

With increased digitalization in power grids, a large amount of data (or “big data”) will be generated and stored for current or future use. As the number of data sources increases, effective acquisition and processing of the data—gathered in large quantities via those sources individually and/or collectively—is of great importance to ensure reliability of the insights drawn from that data [1]. Characterized by the five V’s of big data [2], Big Data Analytics (BDA) in power systems draws data from various data sources and types to enable faster analyses of large quantities of that data. Data considered for BDA purposes can include typical power system measurements [3] as well as nontraditional data drawn from sources not intended for use in the power sector [4].
With the availability of big data in power grids, the usefulness of that data (typically raw data) to draw useful insights via BDA—with powerful big data processing capabilities—has attracted great interest among both academia and industry. Given the large amount of raw data to handle, the choice of applied BDA method for that data is important, as the benefits realized will significantly depend on the selected BDA method. Various BDA methods have been developed, including artificial neural networks, deep learning, reinforcement learning, etc. [5][6].
As the operation and management of electrical energy systems grow more complex, it becomes more financially and functionally beneficial to utilize the new pool of ever-growing data sources and analysis methods. With applications across industries, BDA is presented as a powerful tool for power system operation and management. BDA’s capabilities in working with vast datasets make its use in smart electrical energy systems an important industry development that will aid in the current and future transformations facing the grid. As such, discussions on BDA for smart electrical energy systems are timely and relevant to the evolution of smart energy systems.
With powerful capabilities of BDA in processing data, BDA presents great potential to assist in the planning and operation aspects of energy systems, particularly in the context of the great challenge current and future energy systems face in their transition to a net-zero future. Much of the Low Carbon Technology (LCT)-based equipment will be connected to, distributed across, and operating in modern power grids. Among LCTs, a significant number of electricity-based loads, including Electric Vehicles (EV) and electrical heat pumps, will be integrated into power systems in the very near future [7]. At the same time, conventional power generators, with large system inertia, are shutting down and are being replaced with small-system-inertia, LCT, and intermittent-energy-based generation systems. Driven by carbon footprint reduction goals and related policies, various sectors, including heavy industries, are increasingly becoming electrified, leading to an increased load burden and reliance on the current and future power systems for energy supply. Furthermore, due to increased electrification, including for transport via EVs, and increased generation from intermittent, LCT-based energy resources, large variations in system power flows, including conditions leading to thermal constraints, could be expected—such operations could exacerbate the already aging power system infrastructure, leading to increased system failures and faults. On the other hand, these LCTs are typically interfaced with power systems via power electronic systems, which have high controllability. Thus, these network changes allow for a high degree of flexibility to support effective network management and operation. In current power systems, flexibility resources (such as controllable loads, renewable energy generation, batteries, etc.) have been developed and are purchased to tackle issues that would otherwise require expensive, traditional network reinforcement methods. However, as flexibility resources are increasing in number, existing systems are not able to manage this large amount of flexibility resources and related data efficiently or optimally. In this regard, BDA plays an important role in supporting flexible resource management and smart system operation. BDA has been used to forecast load consumption and renewable energy generation under different network operating scenarios [8][9]. With an accurate forecast of system operation conditions, system operators can better understand their networks’ operating conditions and develop effective strategies to optimally manage the available network resources or optimally purchase the required flexibility resources to achieve greater techno-economic benefits. BDA has been applied to resolve other critical issues, such as estimation and fault diagnosis, to ensure the power systems’ stability [10].

2. Data in Electrical Energy Systems

Data are essential for modern power systems to function properly and for system planners and operators to complete critical functions. Modern data collection in a power system primarily comprises data from customer meters, Phasor Measurement Units (PMUs), utility Supervisory Control and Data Acquisition (SCADA) systems, etc. This data can be utilized to gather the real-time state of the grid as well as allow for formulating effective responses to managing system events or faults. As the number of data sources grows, effective acquisition and processing of large quantities of data becomes imperative for a reliable gathering of insights and for decision making [1].
When applying big data processes, nearly all data are considered useful, since complex analyses can quickly derive valuable insights from large amounts of varied inputs and data types. Therefore, data utilized for big data analysis range extensively, from real-time power system measurements to social media and user traffic as inputs [4].

3. Big Data Analytics in a Power System Context

BDA is a class of techniques used for processing data and performing functions such as K-Nearest Neighbors (KNN), Support Vector Machine (SVM), Decision Tree (DT), Random Forest (RF), Deep Neural Networks (DNN), Long Short-Term Memory (LSTM), etc. BDA has been widely applied in solving various complex problems, including problems such as classification, clustering, pattern recognition, predictive analysis, data forecasting, statistical analysis, natural language processing, etc.

3.1. Big Data Analytics

3.1.1. Artificial Neural Network (ANN)

ANN is among the most popular Artificial Intelligence (AI) approaches that was inspired by biological nervous systems, consisting of neurons and a web of their interconnections. Simple processing elements, emulating a typical biological neuron, and a network of those interconnected elements allow for identification of complex patterns within a set of data, provided as an input, and for storage and quick application of those identified patterns for future use. ANN is usually made of three layers, namely the input layer, output layer, and hidden layer. The input layer takes the data from the network and is connected to the hidden layer and then the output layer. Based on the interconnection of nodes and data movement between the layers, ANN can be classified into two basic categories: the feedforward ANN and the recurrent ANN. In the feedforward ANN, the information moves from input layer to output layer in one direction. The recurrent ANN allows some of the information to move in the opposite direction as well. Figure 1 presents a simplified structure of an ANN that consists of hidden and output layers. Each layer has a set of weights (W) to be assigned and to be applied to the input vector (p); then, a bias vector (b) is added upon the weighted input vector before it is fed into a transfer function (f) for further processing. The output of the transfer function, f, in the hidden layer serves as an input to the output layer; the results generated from the transfer function, f, in the output layer will be the final outputs of an ANN network. The ANN parameters, including weights and biases, are determined by training the ANN, involving a set of data (including both inputs and the expected outputs) fed as an input to the ANN and adjusting the ANN parameters until the ANN outputs match the outputs of the training dataset to a certain desired accuracy [5].
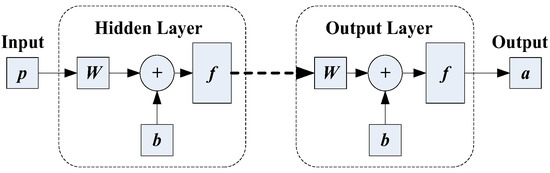
Energies 16 03581 g001 550
Figure 1. Illustration of the structure of an ANN.
ANN has been widely used for various applications in power systems that require identification of a hidden relationship between the known input–output datasets and then applying that identified relationship to an input dataset—with unknown outputs—to quickly predict outputs. With its merit of powerful data analytics, it has been also investigated for the applications of load forecasting, economic dispatch, fault diagnosis, harmonic analyzing, and system security assessment [11].
The ANN structure, such as the network size (e.g., the sizes for the input/output neurons) or the choice of transfer function, is not universal for all applications. The ANN structure should be selected and optimized for the needs of the specific application. With its merits of prediction accuracy and high adaptation, beyond applications in power systems, ANN has also attracted great attention in a wide range of applications in the areas of prediction, clustering, curve fitting, etc.

3.1.2. Deep Learning Techniques

Deep learning techniques have attracted a great deal of attention in the past decade [12] due to their promising results and great accuracy in large-scale pattern recognition, especially in solving visual recognition problems [6]. Deep learning techniques include Multilayer Perceptrons (MLPs), autoencoders, Convolutional Neural Networks (CNNs), LSTM, Recurrent Neural Networks (RNNs), etc.
MLP, as one of the early developed deep learning techniques, is a feedforward neural network with multiple perceptron layers equipped with activation functions. Both input layers and output layers in MLPs are Fully-Connected (FC). MLPs have been popularly applied to image and speech recognition problems.
Autoencoders mainly consist of three components: encoder, coder, and decoder. They are a specific type of feedforward neural network that have identical inputs and outputs. They have been mainly used for image processing, popularity prediction, etc.
CNNs consist of convolution layers that have a set of learnable filters/kernels that slide through input data to extract patterns in the data. Following the convolution layers, an FC neural network is used for classification. In both convolutional layers and neural network layers, multiple layers are typically used to model the complexity of patterns in large data. As one of the most popular deep learning techniques, CNN is popularly used for image recognition. RNNs, which have connections that form directed cycles, allow the outputs to be fed into hidden state as inputs, allowing for the previous inputs to be memorized. RNNs are commonly used for time-series analysis and for natural-language processing problems.
It has been found that deep learning techniques typically perform better than general neural networks, especially in solving multiple data class problems and machine learning applications with complex data structures. To cope with a large amount of data and to facilitate the extraction of more informative features [13], deep learning techniques usually require a relatively large number of hierarchical layers, suggesting the need for a large computational effort [14]. Deep learning techniques, due to the development in high-performance hardware, sometimes specifically designed for faster execution of those techniques, are becoming increasingly popular in various practical applications.
With its powerful pattern recognition capabilities and great accuracy in exacting information from complex data structure (formed by measurements collected from various locations and devices with different sampling frequency), deep learning has great potential in solving various power system problems. For instance, the unsupervised deep learning approach auto-encoder has been applied for load profile classification [15]. CNNs have been used to estimate the state–action value function for controlling residential load control [16], although its application at a system level is limited. Further exploration is needed to fully exploit the powerful capabilities of CNNs in pattern recognition and estimation applications.

3.2. Approaches to Integrate BDA in a Power System Context

Due to the large scale of actual power system/networks, it is impractical, if not impossible, or cost ineffective to have measurements at all desired locations. On the other hand, not all measurement data are useful to achieve a desired application’s objective. Variables/parameters in BDA, therefore, should be carefully selected and processed to ensure usefulness of the collected data specific to a selected or prevailing system scenario.
Furthermore, power system performance highly depends on the topologies and operating conditions that vary constantly. It is desirable that the topology/configuration of power systems can be embedded in the input matrices of the BDA learning mechanisms. Per [17], the System Area Mapping process of feature extraction from the input data matrix was analyzed from a power system configuration perspective. The input matrix was arranged in a way that a patch in the input matrix summarizes the topology information of the corresponding area in the considered power system. Taking a 24-bus test network (given in Figure 2) as an example, different square patches in the input matrix map corresponding areas in the considered power system. Later, by sliding the kernels through these square patches, the features/characteristics in the local area can be extracted and integrated into a higher level in the feature map. Usually, many different kernels will be used in order to extract information from different aspects, capturing a varied set of characteristics and patterns that exist in a considered power system. Through this large set of kernels and through a number of feature extraction layers, useful information captured at a local area will eventually be summarized and integrated into a global area. These approaches should be tailored from a power system context, particularly where the performance of a considered technique as part of the BDA is greatly dependent on the considered power system, its configuration/topology, and its operating conditions.
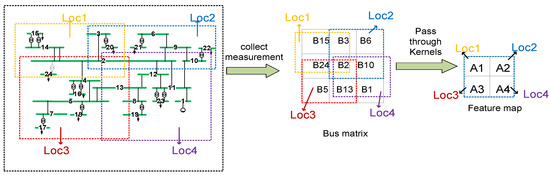
Energies 16 03581 g002 550
Figure 2. Illustration of system area mapping

This entry is adapted from the peer-reviewed paper 10.3390/en16083581

References

  1. Yan, Y.; Sheng, G.; Qiu, R.C.; Jiang, X. Big Data Modeling and Analysis for Power Transmission Equipment: A Novel Random Matrix Theoretical Approach. IEEE Access 2017, 6, 7148–7156.
  2. De Mauro, A.; Greco, M.; Grimaldi, M. A formal definition of Big Data based on its essential features. Libr. Rev. 2016, 65, 122–135.
  3. Zhang, Y.; Huang, T.; Bompard, E.F. Big data analytics in smart grids: A review. Energy Inform. 2018, 1, 8.
  4. Akhavan-Hejazi, H.; Mohsenian-Rad, H. Power systems big data analytics: An assessment of paradigm shift barriers and prospects. Energy Rep. 2018, 4, 91–100.
  5. Gurney, K. An Introduction to Neural Networks; Taylor & Francis, Inc.: London, UK, 1997.
  6. Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90.
  7. BEIS; Ofgem. Transitioning to a Net Zero Energy System: Smart Systems and Flexibility Plan 2021. 2021. Available online: https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/1003778/smart-systems-and-flexibility-plan-2021.pdf (accessed on 16 March 2023).
  8. EPRI. Enhancements to ANNSTLF, EPRI’s Short Term Load Forecaster; Pattern Recognition Technologies, Inc.: Dallas, TX, USA, 1997.
  9. Khotanzad, A.; Afkhami-Rohani, R.; Maratukulam, D. ANNSTLF-Artificial Neural Network Short-Term Load Forecaster-generation three. IEEE Trans. Power Syst. 1998, 13, 1413–1422.
  10. Liao, H.; Anani, N. Fault Identification-based Voltage Sag State Estimation Using Artificial Neural Network. Energy Procedia 2017, 134, 40–47.
  11. Haque, M.T.; Kashtiban, A.M. Application of Neural Networks in Power Systems; A Review. Int. J. Energy Power Eng. 2007, 1, 897–901.
  12. Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324.
  13. Brahma, P.P.; Wu, D.; She, Y. Why Deep Learning Works: A Manifold Disentanglement Perspective. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 1997–2008.
  14. Nielson, M.A. Neural Networks and Deep Learning; Determination Press, 2015; Available online: http://neuralnetworksanddeeplearning.com/ (accessed on 16 March 2023).
  15. Varga, E.D.; Beretka, S.F.; Noce, C.; Sapienza, G. Robust Real-Time Load Profile Encoding and Classification Framework for Efficient Power Systems Operation. IEEE Trans. Power Syst. 2014, 30, 1897–1904.
  16. Claessens, B.J.; Vrancx, P.; Ruelens, F. Convolutional neural networks for automatic state-time feature extraction in reinforcement learning applied to residential load Control. IEEE Trans. Smart Grid 2016, 9, 3259–3269.
  17. Liao, H.; Milanović, J.V.; Rodrigues, M.; Shenfield, A. Voltage Sag Estimation in Sparsely Monitored Power Systems Based on Deep Learning and System Area Mapping. IEEE Trans. Power Deliv. 2018, 33, 3162–3172.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
ScholarVision Creations
Feedback