Deep learning (DL) has been widely studied using various methods across the globe, especially with respect to training methods and network structures, proving highly effective in a wide range of tasks and applications, including image, speech, and text recognition. One important aspect of this advancement is involved in the effort of designing and upgrading neural architectures, which has been consistently attempted thus far. However, designing such architectures requires the combined knowledge and know-how of experts from each relevant discipline and a series of trial-and-error steps. In this light, automated neural architecture search (NAS) methods are increasingly at the center of attention.
- artificial intelligence (AI)
- deep learning (DL)
- convolutional neural network (CNN)
- automated machine learning (Auto-ML)
- neural architecture search (NAS)
1. Introduction
2. Neural Architecture Search
2.1. Search Space
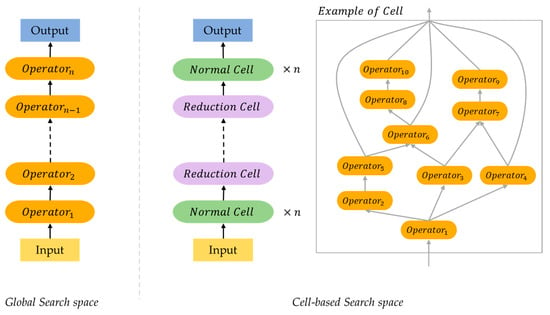
2.1.1. Global Search Space
2.1.2. Cell-Based Search Space
2.2. Search Strategy
2.2.1. Evolutionary Algorithm
| Algorithm 1 GA-based NAS Algorithm |
|
2.2.2. Reinforcement Learning
| S.S. | Application | Performance (ACC, %) and Efficiency | Open Source | |||||
|---|---|---|---|---|---|---|---|---|
| CIFAR-10 | ImageNet | |||||||
| Top-1 | GPU Days | #GPUs | Top-1/5 | GPU Days | #GPUs | |||
| M | ResNet [23] | 93.57 | - | - | 80.62 /95.51 |
- | - | https://github.com/KaimingHe/deep-residual-networks, accessed on 30 July 2016 |
| DenseNet [24] | 96.54 | - | - | 78.54 /94.46 |
- | - | https://github.com/liuzhuang13/DenseNet, accessed on 11 September 2022 | |
| EA | GeNet#2 [29] | 92.9 | 17 | - | 72.13 /90.26 |
17 | - | - |
| RL | MetaQNN [19] | 93.08 | 100 | 10 | - | https://github.com/bowenbaker/metaqnn, accessed on 19 July 2017 | ||
| BlockQNN-Connection more filter [31] | 97.65 | 96 | 32 (1080Ti) |
81.0 /95.42 |
96 | 32 (1080Ti) | - | |
| BlockQNN-Depthwise, N = 3 [31] | 97.35 | |||||||
| ENAS + macro [32] | 96.13 | 0.32 | 1 | - | - | - | https://github.com/melodyguan/enas, accessed on 2 May 2019 | |
| ENAS + micro + c/o [32] | 97.11 | 0.45 | 1 | |||||
| GD | DARTS (1st order) + c/o [33] | 97.00 | 1.5 | 4 (1080Ti) |
73.3 /81.3 |
4 | - | https://github.com/quark0/darts, accessed on 12 October 2018 |
| DARTS (2nd order) + c/o [33] | 97.23 | 4 | ||||||
| DARTS+ [34] | 97.80 | 0.4 | 1 (V100) |
76.10 /92.80 |
6.8 | 1 (P100) |
- | |
| DARTS+ (Large) [34] | 98.32 | - | ||||||
| Fair-DARTS [35] | 97.46 | - | - | 75.6 /92.60 |
3 | - | https://github.com/xiaomi-automl/FairDARTS, accessed on 10 August 2020 | |
| P-DARTS + c/o [36] | 97.50 | 0.3 | - | 75.6 /92.60 |
0.3 | - | https://github.com/chenxin061/pdarts, accessed on 18 February 2020 | |
| P-DARTS (large) + c/o [36] | 97.75 | 0.3 | - | |||||
| Robust DARTS [37] | 97.05 | - | - | - | - | - | https://github.com/automl/RobustDARTS, accessed on 21 July 2020 | |
| Sharp DARTS [38] | 98.07 | 0.8 | 1 (2080Ti) |
74.9 /92.20 |
0.8 | - | - | |
| PC-DARTS + c/o [39] |
97.43 | 0.1 | 1 (1080Ti) |
75.8 /92.70 |
3.8 | 8 (V100) |
https://github.com/yuhuixu1993/PC-DARTS, accessed on 3 July 2020 | |
2.2.3. Gradient Descent (GD)
2.3. Evaluation Strategies
This entry is adapted from the peer-reviewed paper 10.3390/s23031713
References
- McCulloch, W.S.; Pitts, W. A Logical Calculus of the Ideas Immanent in Nervous Activity. Bull. Math. Biophys. 1943, 5, 115–133.
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Comput. 1989, 1, 541–551.
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90.
- ImageNet Large Scale Visual Recognition Competition 2012 (ILSVRC2012). Available online: https://image-net.org/challenges/LSVRC/2012/results.html#t1 (accessed on 21 December 2022).
- Sondhi, P. Feature Construction Methods: A Survey. Sifaka Cs Uiuc Edu. 2009, 69, 70–71.
- Hsu, C.-W.; Chang, C.-C.; Lin, C.-J. A Practical Guide to Support Vector Classification; National Taiwan University: Taipei, China, 2003.
- Hesterman, J.Y.; Caucci, L.; Kupinski, M.A.; Barrett, H.H.; Furenlid, L.R. Maximum-Likelihood Estimation with a Contracting-Grid Search Algorithm. IEEE Trans. Nucl. Sci. 2010, 57, 1077–1084.
- Feurer, M.; Hutter, F. Hyperparameter Optimization. In Automated Machine Learning; Springer: Cham, Switzerland, 2019; pp. 3–33.
- Yu, T.; Zhu, H. Hyper-Parameter Optimization: A Review of Algorithms and Applications. arXiv 2020, arXiv:200305689.
- He, X.; Zhao, K.; Chu, X. AutoML: A Survey of the State-of-the-Art. Knowl.-Based Syst. 2021, 212, 106622.
- Bay, H.; Tuytelaars, T.; Gool, L.V. Surf: Speeded up Robust Features. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2006; pp. 404–417.
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110.
- Dalal, N.; Triggs, B. Histograms of Oriented Gradients for Human Detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 886–893.
- Bishop, G.; Welch, G. An Introduction to the Kalman Filter. Proc SIGGRAPH Course 2001, 8, 41.
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016.
- Yu, F.; Koltun, V. Multi-Scale Context Aggregation by Dilated Convolutions. arXiv 2015, arXiv:151107122.
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258.
- Zoph, B.; Le, Q.V. Neural Architecture Search with Reinforcement Learning. arXiv 2016, arXiv:161101578.
- Baker, B.; Gupta, O.; Naik, N.; Raskar, R. Designing Neural Network Architectures Using Reinforcement Learning. arXiv 2016, arXiv:161102167.
- Liu, H.; Simonyan, K.; Vinyals, O.; Fernando, C.; Kavukcuoglu, K. Hierarchical Representations for Efficient Architecture Search. arXiv 2017, arXiv:171100436.
- Zoph, B.; Vasudevan, V.; Shlens, J.; Le, Q.V. Learning Transferable Architectures for Scalable Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8697–8710.
- Brock, A.; Lim, T.; Ritchie, J.M.; Weston, N. Smash: One-Shot Model Architecture Search through Hypernetworks. arXiv 2017, arXiv:170805344.
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778.
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708.
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Cham, Switzerland, 2015; pp. 234–241.
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826.
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. Shufflenet: An Extremely Efficient Convolutional Neural Network for Mobile Devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6848–6856.
- Rikhtegar, A.; Pooyan, M.; Manzuri-Shalmani, M.T. Genetic Algorithm-Optimised Structure of Convolutional Neural Network for Face Recognition Applications. IET Comput. Vis. 2016, 10, 559–566.
- Xie, L.; Yuille, A. Genetic Cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 1379–1388.
- Dean, J.; Corrado, G.; Monga, R.; Chen, K.; Devin, M.; Mao, M.; Ranzato, M.; Senior, A.; Tucker, P.; Yang, K. Large Scale Distributed Deep Networks. In Proceedings of the NIPS’12: Proceedings of the 25th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012.
- Zhong, Z.; Yan, J.; Wu, W.; Shao, J.; Liu, C.-L. Practical Block-Wise Neural Network Architecture Generation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2423–2432.
- Pham, H.; Guan, M.; Zoph, B.; Le, Q.; Dean, J. Efficient Neural Architecture Search via Parameters Sharing. In Proceedings of the International conference on machine learning, Stockholm, Sweden, 10–15 July 2018; pp. 4095–4104.
- Liu, H.; Simonyan, K.; Yang, Y. Darts: Differentiable Architecture Search. arXiv 2018, arXiv:180609055.
- Liang, H.; Zhang, S.; Sun, J.; He, X.; Huang, W.; Zhuang, K.; Li, Z. Darts+: Improved Differentiable Architecture Search with Early Stopping. arXiv 2019, arXiv:190906035.
- Chu, X.; Zhou, T.; Zhang, B.; Li, J. Fair Darts: Eliminating Unfair Advantages in Differentiable Architecture Search. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2020; pp. 465–480.
- Chen, X.; Xie, L.; Wu, J.; Tian, Q. Progressive Differentiable Architecture Search: Bridging the Depth Gap between Search and Evaluation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 1294–1303.
- Zela, A.; Elsken, T.; Saikia, T.; Marrakchi, Y.; Brox, T.; Hutter, F. Understanding and Robustifying Differentiable Architecture Search. arXiv 2019, arXiv:190909656.
- Hundt, A.; Jain, V.; Hager, G.D. Sharpdarts: Faster and More Accurate Differentiable Architecture Search. arXiv 2019, arXiv:190309900.
- Xu, Y.; Xie, L.; Zhang, X.; Chen, X.; Qi, G.-J.; Tian, Q.; Xiong, H. Pc-Darts: Partial Channel Connections for Memory-Efficient Architecture Search. arXiv 2019, arXiv:190705737.
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement Learning: A Survey. J. Artif. Intell. Res. 1996, 4, 237–285.
- Vermorel, J.; Mohri, M. Multi-Armed Bandit Algorithms and Empirical Evaluation. In European Conference on Machine Learning; Springer: Cham, Switzerland, 2005; pp. 437–448.
- Lin, L.-J. Reinforcement Learning for Robots Using Neural Networks; Carnegie Mellon University: Pittsburgh, PA, USA, 1992.
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9.
- Real, E.; Moore, S.; Selle, A.; Saxena, S.; Suematsu, Y.L.; Tan, J.; Le, Q.V.; Kurakin, A. Large-Scale Evolution of Image Classifiers. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 2902–2911.
- Shin, R.; Packer, C.; Song, D. Differentiable Neural Network Architecture Search. 2018. Available online: https://openreview.net/forum?id=BJ-MRKkwG (accessed on 21 December 2022).
- Saxena, S.; Verbeek, J. Convolutional Neural Fabrics. arXiv 2016, arXiv:1606.02492.
- Ahmed, K.; Torresani, L. Connectivity Learning in Multi-Branch Networks. arXiv 2017, arXiv:170909582.
- Veniat, T.; Denoyer, L. Learning Time/Memory-Efficient Deep Architectures with Budgeted Super Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3492–3500.
- Achille, A.; Rovere, M.; Soatto, S. Critical Learning Periods in Deep Networks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018.
- Frankle, J.; Schwab, D.J.; Morcos, A.S. The Early Phase of Neural Network Training. arXiv 2020, arXiv:200210365.
- Santra, S.; Hsieh, J.-W.; Lin, C.-F. Gradient Descent Effects on Differential Neural Architecture Search: A Survey. IEEE Access 2021, 9, 89602–89618.
- Klein, A.; Falkner, S.; Springenberg, J.T.; Hutter, F. Learning Curve Prediction with Bayesian Neural Networks. In Proceedings of the ICLP 2017, Melbourne, Australia, 28 August–3 September 2017.
- Deng, B.; Yan, J.; Lin, D. Peephole: Predicting Network Performance before Training. arXiv 2017, arXiv:171203351.
- Domhan, T.; Springenberg, J.T.; Hutter, F. Speeding up Automatic Hyperparameter Optimization of Deep Neural Networks by Extrapolation of Learning Curves. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July2015.
- Chen, T.; Goodfellow, I.; Shlens, J. Net2net: Accelerating Learning via Knowledge Transfer. arXiv 2015, arXiv:151105641.
- Wei, T.; Wang, C.; Rui, Y.; Chen, C.W. Network Morphism. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 564–572.
- Stamoulis, D.; Ding, R.; Wang, D.; Lymberopoulos, D.; Priyantha, B.; Liu, J.; Marculescu, D. Single-Path Nas: Designing Hardware-Efficient Convnets in Less than 4 Hours. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases; Springer: Cham, Switzerland, 2020; pp. 481–497.
- Moser, B.; Raue, F.; Hees, J.; Dengel, A. Less Is More: Proxy Datasets in NAS Approaches. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 1953–1961.
- Xu, Y.; Wang, Y.; Han, K.; Tang, Y.; Jui, S.; Xu, C.; Xu, C. Renas: Relativistic Evaluation of Neural Architecture Search. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 4411–4420.
- Chen, Y.; Guo, Y.; Chen, Q.; Li, M.; Zeng, W.; Wang, Y.; Tan, M. Contrastive Neural Architecture Search with Neural Architecture Comparators. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 9502–9511.
- Zhang, Y.; Li, B.; Tan, Y.; Jian, S. Evaluation Ranking Is More Important for NAS. In Proceedings of the 2022 IEEE International Joint Conference on Neural Networks (IJCNN), Padova, Italy, 18–23 July 2022; pp. 1–8.
