The type of microgrid (MG) system can be classified into feeder and facility MGs. A feeder-based MG mainly operates in synchronized operation with the distribution feeder or surrounding utilities to provide additional power injections, reactive power support, and ancillary service for enhancing the reliability of the electricity service. In contrast, a facility-based MG is proposed to ensure energy resilience for communities, specifically for critical loads or customers. Such an MG system can be operated both in grid-tied and autonomous modes during contingency periods due to extreme weather events.

The selection of MG architectures is a key issue. The architecture of the MG needs to be selected carefully to obtain the most benefits from the MG. The typical configuration of the MG system can mainly be classified into three groups according to the appearance of AC and DC buses. It can be categorized into the AC-microgrid (AC-MG), DC-microgrid (DC-MG), and AC-DC-microgrid (AC-DC-MG). In AC-MG, the operational voltage and current are in the AC form. Therefore, interfacing devices must be used to connect RE-based DG units to the AC bus. Hence, most of the RE-based DG units deploy DC/AC power electronic converters.

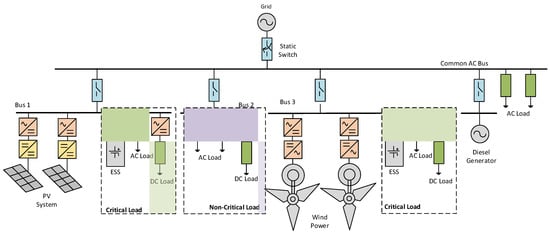
Figure 1 shows an example of the AC-MG system. The AC-MG usually consists of three buses where critical loads are integrated at buses 1 and 3, while noncritical loads are connected to bus 2. RE-based DG units (PV and wind) and energy storage systems (ESSs) are interfaced to the associated bus by a DC/AC converter to form the AC-MG. To ensure the power balance and overcome the shortfall in energy from RE-based DG units, a diesel generator, preferably a biodiesel generator (BDG), could be integrated. In the grid-tied operation, the AC power may flow directly from/to the MG system without an additional conversion process. Direct coupling between the main grid and the AC-MG ensures a synchronized operation of each DG unit within the MG and the main grid. Therefore, it is easier to maintain the local voltage and frequency as the main grid. On the other hand, in a DC-MG, an additional conversion process through the bidirectional DC/AC converter is required to facilitate grid-tied operation. Voltage and frequency deviations potentially emerge if the bidirectional converter fails to maintain the synchronized operation with the main grid. When those deviations cannot be restored, the MG system has to be disconnected from the grid to maintain the stability of the primary grid. Consequently, the electricity service is perturbed, and hence the system’s reliability could deteriorate. Furthermore, load, DG units, and ESS must follow the grid conditions [8]. The AC-MG system is feasible for both RE and non-RE-based DG units. It can be used in many applications, such as remote areas and commercial buildings, and as a backup for existing power systems [21].

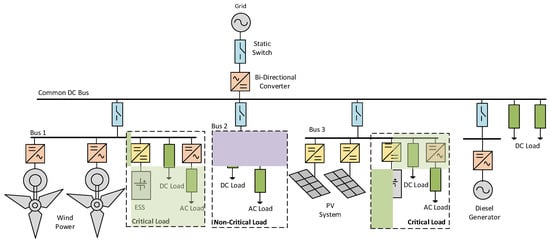
Figure 2 represents a typical structure of the DC-MG. Integration of the DC-MG into the main grid is provided by means of a bidirectional DC/AC converter system to facilitate power exchange between MG and the main grid. The RE-based DG units, ESS, and variable DC and AC loads are connected to DC buses through an AC/DC rectifier and DC/DC converter system. Two critical load buses with RE-based generators are presented in Figure 2. All the load-generation buses are connected to the point of common coupling or the main backbone of the system referred to as the DC common bus. The DC-MG offers several advantages over the AC-MG. First, simpler interface connections such as one stage DC/DC converter in a PV system and ESS and an AC/DC rectifier in the wind may reduce the number of power electronic devices, therefore enhancing the overall efficacy of the MG system. The DC-MG enables the provision of regulated DC voltage. Therefore, some DC loads can be connected directly to the DC bus. In grid-connected operation, synchronization is only required in the bidirectional DC/AC converter system, which connects the DC-MG to the grid. Moreover, these features bring simplification to the overall DC-MG control schemes.

The primary consideration in the DC-MG is the bidirectional DC/AC converter, which facilitates a connection between the DC-MG and the main grid. This device handles the whole power flow from/to the main grid. Therefore, it requires highly rated power electronic devices. Moreover, the highly-rated bidirectional converter system may influence the system’s reliability. Another concern in the DC-MG is that the DC/AC converter system required to connect AC loads to the MG and DC load needs to be standardized. Thus, an additional power conversion stage is required to adjust the DC bus level or to generate the required AC voltage [8].

The AC-DC-MG configuration is composed of AC and DC buses with a bidirectional DC/AC converter. In this typical configuration, the load/generation buses (bus 1 and 2) are connected via switches to the backbone of the network (i.e., common AC bus). This architecture combines the advantages of the AC-MG and DC-MG and compensates for the drawbacks of the system. Reliability is improved since there is a direct connection between the AC feeder and the grid. The DC feeder also provides simplification to the power electronic device structures. Various loads can be connected to the appropriate feeder. The AC load can be connected directly to the AC feeder or by means of DC/AC voltage converter in the DC feeder. The DC load can be directly connected to the DC feeder without a power converter. This configuration is suitable for MGs, which supply critical loads for specific purposes.

Power electronic devices become the inevitable elements of RE-based DG units to convert the generated DC power to AC power. Moreover, this equipment is responsible for maintaining DG units’ output voltage and frequency at desired values. In addition, the power electronic devices’ fast-switching action enables the DG units’ ride-through. Therefore, a detailed mathematical model of each RE-based DG unit involving power electronic devices and associated controllers is required to obtain complete dynamic characteristics of the MG system.

A general mathematical model of power electronic switches in an AC/DC converter system was derived in [22]. The developed model considered the detailed modulation technique. Therefore, the proposed model is time-variant, nonlinear, and complex. To overcome these difficulties, the Fourier transform method was deployed to represent the switching actions of power electronic devices. The switching action was represented by modulation indices [23]. The steady-state operating point and dynamic response of the AC/DC converter could be determined separately from these models. Fourier transform’s eminent low- and high-frequency AC/DC converter models are on the switching frequency boundary. The high-frequency model is used to evaluate the harmonic components. The low-frequency model was linearized and transformed into a rotating reference frame to obtain a time-invariant steady-state and small-signal model.

Dynamic models of the single-phase and three-phase voltage source converter are presented in [12,24]. For the three-phase converter, modulation indices were treated as control variables of the converter, i.e., time-averaged switching duty cycles. The resulting small-signal model is time-variant due to the presence of periodic switching actions. Hence, transformation into a rotating reference frame must be conducted to obtain a time-invariant small-signal model, as depicted in [12,15,25]. A detailed representation of time-averaged switching components of the PWM control scheme has been studied and reported in [12]. Eigenvalue analysis displayed the movements of weak modes under small variations in modulation indices, indicating the dynamic characteristics of the converter system due to small variations of the control signal.

The MG stability can be categorized into transient, voltage, and small-signal stability issues [11,28]. The transient stability of the MG corresponds to the ability of the MG system to maintain stability after being subjected to significant disturbances such as a structural change in MG due to the outage of a particular DG unit, short circuit faults, and switching operation mode from grid-tied to islanding operation. The MG’s capability to maintain voltage within specified limits is known as voltage stability. Voltage instability concerns in MGs are highly correlated to reactive power balance conditions, dynamic load connections, the reactive power limit, and tap changer operations [29,30]. However, due to the small size and high R/X ratio, the voltage regulation of the MG could be influenced by the active power modulation in the MG. MGs are susceptible to small perturbations due to the cluster of RE-based DG units with fewer or no physical inertia features. The low physical inertia is mainly observed due to the wide deployment of power electronic devices in most RE-based DG units [11,31].

Small-signal stability in MGs can arise from various sources such as continuous fluctuations of the RE-based system, the feedback controller, the small change in load, parameter variations, and a lack of damping due to the low-inertia characteristics of MG [11]. Smaller controller gain variations in a conventional power system with strong inertia features do not significantly affect the equilibrium point and stability margin [35]. Conversely, small changes in RE values, load demand, and system parameters involving controller gain in an MG system may lead to the undamped oscillatory condition under small disturbances [36,37,38,39]. Due to an assumption that the MG system is usually connected to a strong grid, small-signal instability could be one of the primary concerns for the islanded operation mode of the MG system [36,37,40,41,42,43,44]. This assumption is expected to change soon due to the reduction in the system strength in an interconnected transmission system with incremental penetration of the converter-based generator. In addition, inaccurate power sharing among DG units and high loading conditions within MGs potentially result in undamped oscillation, leading to instability [3].

Considering different assumptions involving different approaches to model power electronic devices to build the dynamic model of the MG system could provide diverse results corresponding to the source of small-signal stability in MGs. The critical modes might emerge from various state variables. In [41], a simplified model of converter-based DG units was developed to investigate the trajectories of the sensitive modes under a variation in active and reactive power controller gains and cut-off frequency. It was reported that the selection of a higher cut-off frequency improved the dynamic system responses. On the other hand, this frequency setting could lead to the avoidance of power signal ripples. Hence, it does not contribute to system instability.

A small-signal model of the MG system with three converter-based DG units is presented in [38,45]. It was observed that with the simplified model of switching devices and control systems, only the critical mode from the power controller’s state variable was identified. It was reported that the change in the power-sharing scheme, which was reflected in the change of droop gain values, affected the oscillatory stability of the MG. The variation in active power droop gain control introduced a significant impact on MG dynamic responses than the variation in reactive power droop gain. Therefore, low-frequency oscillations are mainly determined by the droop controllers of the DG unit.

The developed model in [38] was then improved with an additional phase-locked loop (PLL) block, as presented in [44]. The PLL contributes to the damping of the oscillatory modes, even though variation of droop gain control might cause instability issues to the MG systems. It is reported that the low-frequency eigenvalues are sensitive to a variation in droop gain and network configuration, while high-frequency modes are largely susceptible to inner controller gain. However, the dynamics from power electronic devices were disregarded due to the consideration of the ideal characteristics of the converter.

Small-signal stability analysis of electronically coupled and conventional DG units in MGs is presented in [32,36]. The obtained results in [32] suggest that the MG dynamic responses are influenced by system configuration and variability of generated power from each DG unit. Moreover, the ESS significantly enhanced the oscillatory stability margin of the MG by mitigating the instantaneous active/reactive power imbalance. In [36], a systematic approach and mathematical formulations for small-signal stability studies, including synchronous machines and converter-based DG units, are presented. It was revealed that the frequency deviation and oscillation on the electronically coupled DG unit occurred due to an increase in controller gains. Additional critical modes are observed when the MG operates in an islanded operation mode. The gain constant of PLL is identified as the source of the oscillatory mode. Governor control action in the synchronous machine provided frequency restoration for the MG system.

It is important to consider various loads and load parameter uncertainties for small-signal stability assessment of the MG systems [10,46,47,48]. Dynamic characteristics of converter-based DG units in MG under different load characteristics, such as inductive passive and active loads, are presented in [10,38,44,46,47,48]. The developed small-signal model in [38] was employed in [10,46] to investigate the influence of active loads on the oscillatory stability of MGs. Incorporating an active load in the small-signal stability model of autonomous MG operation could introduce small stability/instability concerns, specifically when interaction happens between the active load and converter-based DG unit [10]. Moreover, the large gain setting of the active load voltage controller leads to instability conditions. It was clearly seen that active load severely affects the oscillatory stability of the MG. Deterioration of a small-signal stability margin was monitored when a dynamic load such as an induction motor (IM) was connected to the MG [47,48]. Low-frequency oscillation of electromechanical modes of a large IM resulted in undesirable dynamic responses and poor small-signal stability performance of the MG in islanded operation mode [48]. The presence of an IM might cause an admittance mismatch between the IM load and the MG. This mismatch could destabilize the islanding operation due to the coupling between the IM and the converter. An active compensation technique based on the Nyquist stabilization criterion has been proposed to maintain the stability of the system. This method provides simplicity and positively influences the power-frequency oscillation of DG units in isolated operations. A two-DOF (degrees of freedom) active damping control algorithm was proposed in [47] to mitigate low-frequency oscillation. The transient supplementary power angle and voltage magnitude signals are effectively used to damp the MG frequency and voltage oscillations without affecting the steady-state power-sharing characteristics.

Different dynamic responses from DG units could be observed when various RE-based power generators are integrated into an MG system. Those distinct dynamic characteristics cannot be captured using the simplified model of MG systems. However, in most studies, power electronic devices in DG units are usually presented as ideal voltage/current sources [10,38,45,49]. Therefore, it is difficult to monitor the typical dynamic characteristics of different power electronic device architectures in a particular DG unit [15,36,37]. The detailed MG model was primarily developed in [40]. However, the control systems were not considered in those presented models. Moreover, in an MG system with a cluster of DG units, a sophisticated MG control algorithm introduces more nonlinear effects on modal behaviour, potentially leading to interaction among sensitive modes [6,7,50].

A more detailed model of an RE-based DG unit provides a complete representation of the small-signal stability performance of MG systems. In [28,39,51], a detailed MG system consisting of a detailed model of a wind (Type 4 with AC-DC-AC converter), PV (two-stages with DC-DC and DC-AC converter), and diesel generator with LCL filters and generic controllers is presented. It was reported that the risk of instability could be increased from gain controller adjustment. The DC link and the voltage and current controller gains could also affect the MG system’s small-signal stability. The critical modes vary significantly with the variation in associated droop and gain of the controllers.

The small-signal stability performance of the DC MG is presented in [33,34]. The DC MG is modelled using an average model of the parallel DC-DC converter. Impedance analysis was performed in a system with parallel converters. In [49,52], a small-signal model of a DC/AC converter with static droop characteristics (combined with an adaptive transient droop function) was considered. Similar to the AC MG, in the DC MG, there are critical modes. These modes are characterized by low-frequency modes, mainly determined by the droop controllers of the DG unit. It was also reported that oscillatory conditions depend on the parameters of converters and controllers, line impedance, and load [53]. Low-frequency modes are dictated mainly by the power-sharing controllers and the power filters [49,52]. Load proportion could significantly affect the small-signal stability performance of the DC MG. Trajectories of eigenvalues suggested that a high portion of constant power load (CPL) could adversely affect the damping of the DC MG due to its negative impedance characteristic [54,55,56,57,58]. Conversely, the constant resistive load (CRL) increases the damping characteristics of the MG.

The uncertainty of renewable sources also contributes to the dynamic behaviour of the MG system. Critical modes within the MG might fluctuate randomly with uncertainties associated with renewable sources. In [59], the trajectories of critical modes under uncertain wind speed conditions in a wind–diesel MG system were investigated. It was observed that at a higher wind speed variation, the small-signal stability performance of the MG deteriorated severely. The dynamic performance also deteriorated considerably when each wind-based DG unit in MG was subjected to different wind speeds compared to a similar wind speed regime. The effects of mixture uncertainties from wind speed and solar irradiance on small-signal stability of MG systems are presented in [6,60,61,62]. Conventional and copula methods were implemented in estimating the probability density function (pdf) of wind speed and solar irradiance, considering the possible correlation between those two renewable sources for small-signal stability assessment.