Encyclopedia
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects:
Engineering, Electrical & Electronic
FBG sensors are increasingly commercially available and are, one of the most popular sensors from the fiber optic sensing family, having found use in a variety of industrial and research applications. A conventional FBG sensor is made up of a specially fabricated small and flexible segment imprinted into the core of a single-mode optical fiber.
- Fiber Bragg grating (FBG)
- fiber optic sensors
- electric machines
- drives
1. Introduction
The condition monitoring of electrical machinery is progressively gaining importance as the utilization of electric machines is increasing at an unprecedented scale, driven considerably by the proliferation of renewable power generation, transport electrification, and the ongoing automation of industrial processes [1,2]. Conventional condition monitoring (CM) methods for electrical machines have significant limitations in providing the levels of diagnostic reliability required for maintaining future mission-critical machine applications in service. This primarily concerns the delivery of a diagnosis that can allow for the prevention or minimization of costly and unnecessary outages (e.g., wind turbine generators), as well as the reduction in any related safety concerns in specific demanding applications (e.g., electric propulsion).
It is generally desirable in practical applications for CM systems to be as non-invasive as possible: this can often contradict the aim of reliable diagnosis, which largely depends on sensing access to key localized physical measurands that optimally characterize a particular failure process (e.g., heat, strain, etc.). Conventional CM is not optimally suited to this, as it relies heavily on the analysis of diagnostic data collected through the application of limited sensing devices that are frequently not optimally placed to capture or characterize a localized fault process. This is particularly valid where sensing implementation in locations within the electric machine geometry is concerned. In situ sensing in the vicinity of known failure points or in known stress areas, could yield a much better understanding and monitoring of critical diagnostic measurements. This could, in turn, enable a much-improved characterization of the fault process inception and its propagation stages to ultimately yield an improved reliability diagnosis [3,4,5]. The availability of such in situ sensing abilities would not only enable better diagnostics but would be of use in machine design and prototyping stages for the high fidelity characterization of the device operating performance envelope and make it possible to improve the machine design process and perform a more thorough evaluation of machine stress and performance models [6,7]. Neither of these can be supported by the conventional sensing that is commonly employed in standard electric machine CM schemes, where sensing limitations can prevent the better utilization of CM for a more reliable and timely diagnosis [2,8,9]. There is, therefore, a significant amount of interest in the development of multi-physical embedded sensing alternatives for electric machine CMs, including the observation of a range of multi-physical parameters (e.g., thermal, strain, flux, etc.) to permit the advanced monitoring and understanding of essential stress measurands.
Fiber optic fiber Bragg grating (FBG) sensing technology has been emerging as a strong alternative that could provide solutions for advanced in situ sensing within electric machine geometries. Its inherent features of electromagnetic interference (EMI) immunity, small size, power passivity, flexibility, and ability to multiplex sensing provide opportunities to overcome many of the existing limitations with sensing used in electric machine CMs [10,11,12]. While FBG sensors are inherently responsive to mechanical and thermal excitation, they can be adapted to measure other physical phenomena of interest in electromagnetic rotary devices, such as through the integration of magnetostrictive material for magnetic flux measurement [13,14,15]. Despite the wider adoption of FBG sensing in electric machinery still being stifled by its relatively high cost, much effort has been reported in recent years on exploring effective ways to implement FBGs in various electric machine types to enable advanced multi-physical in situ sensing. This is extended to other associated power equipment where the unique FBG sensing features invariably present attractive opportunities for the in-service observation of high-fidelity device measurements.
2. Operating Principles of FBG Sensors
FBG sensors are increasingly commercially available and are, today, one of the most popular sensors from the fiber optic sensing family, having found use in a variety of industrial and research applications. A conventional FBG sensor is made up of a specially fabricated small and flexible segment imprinted into the core of a single-mode optical fiber, as illustrated in Figure 1.
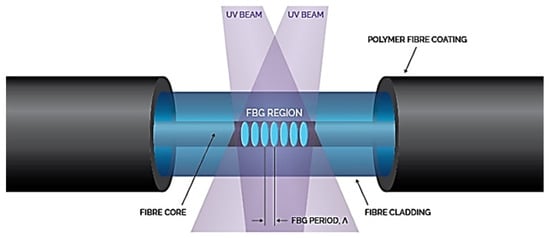
Figure 1. Structure of an FBG sensor [16].
Figure 1 shows a typical FBG sensor structure, with a single-mode optical fiber containing a cylindrical core (glass, from 4 to 9 µm in diameter) which is surrounded by a cladding layer (glass, 125 µm in diameter). The purpose of the cladding layer is to confine light propagation within the glass core and limit optical losses. Furthermore, the top coating layer, which is generally made of acrylate or polyimide, is applied to strengthen the fiber. The sensing part of the structure is denoted as the FBG sensing head and comprises an equidistant sequence of gratings, which are UV (ultraviolet) laser-induced modulations in the glass core refractive index during FBG fabrication. The length of the FBG sensor (FBG head length) is defined by the number of gratings and the distance between them (grating period Ʌ) and is typically in a range from 1 to 20 mm [17]. Multiple sensing heads can be manufactured on the same fiber in a variety of available structures to provide a multiplexed sensor array on a single fiber strand.
When the fiber is illuminated by broadband light, the gratings reflect a specific light spectrum (i.e., the Bragg wavelength, λB), which varies with the thermal and mechanical conditions that the sensing head is exposed to. The light wavelength that is reflected meets the Bragg condition as set by the grating structure, while the rest of the light spectrum is transmitted through the FBG head. The operation principle of an FBG sensor is illustrated in Figure 2, where λB is the calculated peak mid-point of the reflected wavelength. Assuming other relevant application conditions are satisfied, monitoring the reflected spectrum can enable the FBG head to principally be utilized as a thermal and/or mechanical sensing device with the advantages of EMI immunity, a small size, and flexibility.
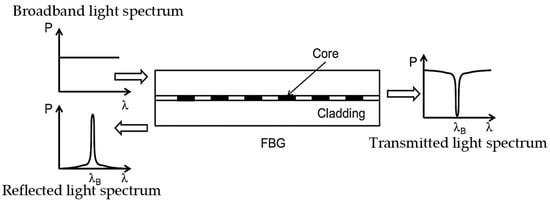
Figure 2. Operating principles of FBG.
In a sensing application, an FBG head reflects a specific wavelength of light from a distinct fiber location exposed to physical excitation, such as temperature, strain, etc. The measurement process involves the observation and measurement of the reflected wavelength using a specialized optoelectronic interrogator device. Once acquired, the reflected wavelength is converted to a set physical measurand, based on a pre-calibrated wavelength for the physical excitation relationship [15,18]. In principle, an interrogator is responsible for illuminating the fiber, and subsequently, for successfully receiving and monitoring the reflected Bragg wavelength(s). Depending on the nature of a particular sensing application, the interrogator needs to capture any rapid changes in the wavelength, and therefore, different techniques are available for the effective tracking of the relative changes in λB. Overall, the general characteristics that are required from the integrator used in FBG sensing are high resolution, high accuracy, usually within the range of pico meters, multiplexing ability, and acceptable cost. In addition, the calibration process of the wavelength shift to the physical measurement value is imperative for enabling FBG sensing applications [11,19]. This involves the exposure of the sensor to a controlled range of the physical measurand to be observed, and the characterization of the reflected wavelength to the physical measurand value relationship. Where possible, calibration is performed on free FBG fibers, however, some applications can require in situ sensor calibration, which can be challenging due to the sensor being embedded within a device and the use of any required sensor-to-device structure bonding media.
A typical reflected wavelength spectrum of an FBG sensor is illustrated in Figure 3.
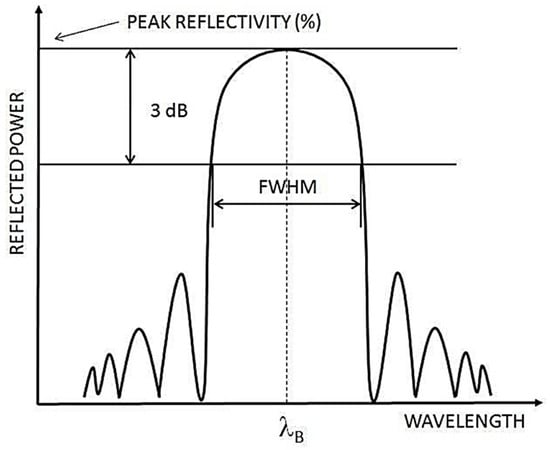
Figure 3. A reflected wavelength spectrum of a typical FBG sensor [20].
The bandwidth of the FBG sensor reflection is defined as its full width at half maximum (FWHM) and is the reflected spectra width at 50% or −3 dB from the peak reflection point. The bandwidth of an FBG sensor is dependent on a number of FBG structure parameters, notably the grating number and spacing [20]. The peak wavelength of the reflected narrowband is the Bragg reflection wavelength, λB, which is dependent on the effective refractive index of the optical fiber (neff) and the Bragg grating period (Λ, i.e., the spacing between successive gratings) and can be calculated as [17]:
λB = 2 neff Λ
Any change in the observed measurand, such as strain and temperature, results in a corresponding change in neff and Λ, and therefore, results in a consequent variation in λB, which is calculated as [17]:
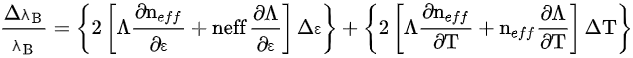
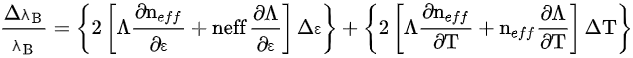
In (2): ΔλB is the relative change in the reflected Bragg wavelength, ε is the strain, and T is temperature. The first term in brackets in (2) is related to the Bragg wavelength shift caused by the strain-induced elastic-optic effect, whereas thermo-optic and thermal expansion caused by the Bragg wavelength variation are represented in the second term in (2). For ease of interpretation, Equation (2) can be presented in the literature be in its condensed form as:
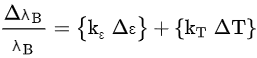where kε is the total strain and kT is the total temperature sensitivity factor of the FBG sensor.
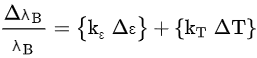
This entry is adapted from the peer-reviewed paper 10.3390/machines10111103
This entry is offline, you can click here to edit this entry!
