A turn is a unit of plane angle measurement equal to 2π radians, 360 degrees or 400 gradians. A turn is also referred to as a cycle (abbreviated cyc), revolution (abbreviated rev), complete rotation (abbreviated rot) or full circle. Subdivisions of a turn include half turns, quarter turns, centiturns, milliturns, points, etc.
- angle measurement
- milliturns
- revolution
1. Subdivision of Turns
A turn can be divided in 100 centiturns or 1000 milliturns, with each milliturn corresponding to an angle of 0.36°, which can also be written as 21′ 36″. A protractor divided in centiturns is normally called a percentage protractor.
Binary fractions of a turn are also used. Sailors have traditionally divided a turn into 32 compass points. The binary degree, also known as the binary radian (or brad), is 1⁄256 turn.[1] The binary degree is used in computing so that an angle can be represented to the maximum possible precision in a single byte. Other measures of angle used in computing may be based on dividing one whole turn into 2n equal parts for other values of n.[2]
The notion of turn is commonly used for planar rotations.
2. History
The word turn originates via Latin and French from the Greek word τόρνος (tórnos – a lathe).
In 1697, David Gregory used π/ρ (pi over rho) to denote the perimeter of a circle (i.e., the circumference) divided by its radius.[3][4] However, earlier in 1647, William Oughtred had used δ/π (delta over pi) for the ratio of the diameter to perimeter. The first use of the symbol π on its own with its present meaning (of perimeter divided by diameter) was in 1706 by the Welsh mathematician William Jones.[5] Euler adopted the symbol with that meaning in 1737, leading to its widespread use.
Percentage protractors have existed since 1922,[6] but the terms centiturns and milliturns were introduced much later by Fred Hoyle.[7]
The German standard DIN 1315 (1974-03) proposed the unit symbol pla (from Latin: plenus angulus "full angle") for turns.[8][9] Since 2011, the HP 39gII and HP Prime support the unit symbol tr for turns. In 2016, support for turns was also added to newRPL for the HP 50g.[10] In June 2017, for release 3.6, the Python programming language adopted the name tau to represent the number of radians in a turn.[11]
The standard ISO 80000-3:2006 mentions that the unit name revolution with symbol r is used with rotating machines, as well as using the term turn to mean a full rotation. The standard IEEE 260.1:2004 also uses the unit name rotation and symbol r.
3. Unit Conversion
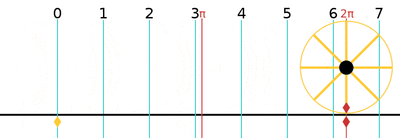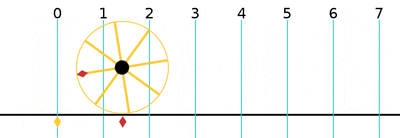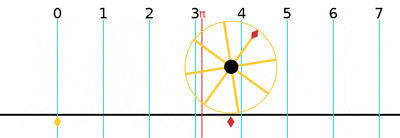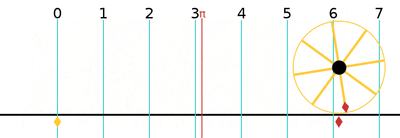
One turn is equal to 2π (≈ 6.283185307179586)[12] radians.
| Turns | Radians | Degrees | Gradians, or gons |
|---|---|---|---|
| 0 | 0 | 0° | 0g |
| 1/24 | π/12 | 15° | 16+2/3g |
| 1/12 | π/6 | 30° | 33+1/3g |
| 1/10 | π/5 | 36° | 40g |
| 1/8 | π/4 | 45° | 50g |
| 1/2π | 1 | c. 57.3° | c. 63.7g |
| 1/6 | π/3 | 60° | 66+2/3g |
| 1/5 | 2π/5 | 72° | 80g |
| 1/4 | π/2 | 90° | 100g |
| 1/3 | 2π/3 | 120° | 133+1/3g |
| 2/5 | 4π/5 | 144° | 160g |
| 1/2 | π | 180° | 200g |
| 3/4 | 3π/2 | 270° | 300g |
| 1 | 2π | 360° | 400g |
4. Tau Proposals

In 2001, Robert Palais proposed using the number of radians in a turn as the fundamental circle constant instead of π, which amounts to the number of radians in half a turn, in order to make mathematics simpler and more intuitive. His proposal used a "pi with three legs" symbol to denote the constant ([math]\displaystyle{ \pi\!\;\!\!\!\pi }[/math] = 2π).[13]
In 2010, Michael Hartl proposed to use tau to represent Palais' circle constant: Template:Tau = 2π. He offered two reasons. First, Template:Tau is the number of radians in one turn, which allows fractions of a turn to be expressed more directly: for instance, a 3/4 turn would be represented as 3/4Template:Tau rad instead of 3/2π rad. Second, Template:Tau visually resembles π, whose association with the circle constant is unavoidable.[14] Hartl's Tau Manifesto[15] gives many examples of formulas that are asserted to be clearer where tau is used instead of pi.[16][17][18]
The proposal is implemented in the Google calculator and in several computer programs like Python[19], Perl[20], Processing[21], and Nim[22]. It has also been used in at least one mathematical research article,[23] authored by the Template:Tau-promoter P. Harremoës.[24]
However, none of these proposals have received widespread acceptance by the mathematical and scientific communities.[25]
5. Examples of Use
- As an angular unit, the turn or revolution is particularly useful for large angles, such as in connection with electromagnetic coils and rotating objects. See also winding number.
- The angular speed of rotating machinery, such as automobile engines, is commonly measured in revolutions per minute or RPM.
- Turn is used in complex dynamics for measure of external and internal angles. The sum of external angles of a polygon equals one turn. Angle doubling map is used.
- Pie charts illustrate proportions of a whole as fractions of a turn. Each one percent is shown as an angle of one centiturn.
6. Kinematics of Turns
In kinematics, a turn is a rotation less than a full revolution. A turn may be represented in a mathematical model that uses expressions of complex numbers or quaternions. In the complex plane every non-zero number has a polar coordinate expression z = r cis(a) = r cos(a) + ri sin(a) where r > 0 and a is in [0, 2π). A turn of the complex plane arises from multiplying z = x + iy by an element u = ebi that lies on the unit circle:
- z ↦ uz.
Frank Morley consistently referred to elements of the unit circle as turns in the book Inversive Geometry, (1933) which he coauthored with his son Frank Vigor Morley.[26]
The Latin term for turn is versor, which is a quaternion that can be visualized as an arc of a great circle. The product of two versors can be compared to a spherical triangle where two sides add to the third. For the kinematics of rotation in three dimensions, see quaternions and spatial rotation.
The content is sourced from: https://handwiki.org/wiki/Turn_(geometry)
References
- "ooPIC Programmer's Guide". www.oopic.com. Archived from the original on 2008-06-28. https://web.archive.org/web/20080628051746/http://www.oopic.com/pgchap15.htm.
- "Angles, integers, and modulo arithmetic". blogs.msdn.com. http://blogs.msdn.com/shawnhar/archive/2010/01/04/angles-integers-and-modulo-arithmetic.aspx.
- A History of Pi. Barnes & Noble Publishing. 1989.
- The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English. The Mathematical Association of America. 1994. p. 165.
- "Pi through the ages". http://www.veling.nl/anne/templars/Pi_through_the_ages.html.
- "A Percentage Protractor". Journal of the American Statistical Association 18: 108–109. 1922. doi:10.1080/01621459.1922.10502455. https://dx.doi.org/10.1080%2F01621459.1922.10502455
- Astronomy. London: Macdonald. 1962.
- (in German) Handbuch SI-Einheiten: Definition, Realisierung, Bewahrung und Weitergabe der SI-Einheiten, Grundlagen der Präzisionsmeßtechnik (1 ed.). Friedrich Vieweg & Sohn Verlagsgesellschaft mbH, reprint: Springer-Verlag. 2013-03-13. 978-3-528-08441-7, 9783322836069. ISBN 3322836061. https://books.google.com/books?id=63qcBgAAQBAJ&pg=PA421. Retrieved 2015-08-14.
- (in German) Das Vieweg Einheiten-Lexikon: Formeln und Begriffe aus Physik, Chemie und Technik (1 ed.). Vieweg, reprint: Springer-Verlag. 2013-03-09. doi:10.1007/978-3-322-92920-4. 978-3-322-92921-1. ISBN 3322929205. https://books.google.com/books?id=2zecBgAAQBAJ. Retrieved 2015-08-14.
- http://www.hpmuseum.org/forum/thread-4783-post-55836.html#pid55836
- https://www.python.org/dev/peps/pep-0628/
- Sequence OEIS: A019692
- "Pi is Wrong". The Mathematical Intelligencer (New York, USA: Springer-Verlag) 23 (3): 7–8. 2001. doi:10.1007/bf03026846. http://www.math.utah.edu/%7Epalais/pi.pdf.
- "The Tau Manifesto". 2013-03-14. http://tauday.com/tau-manifesto.
- https://hexnet.org/files/documents/tau-manifesto.pdf
- "Interview: Michael Hartl: It's time to kill off pi". New Scientist 209 (2794): 23. 2011-01-08. doi:10.1016/S0262-4079(11)60036-5. Bibcode: 2011NewSc.209...23A. https://dx.doi.org/10.1016%2FS0262-4079%2811%2960036-5
- "On Pi Day, is 'pi' under attack?". cnn.com. 2011-03-14. http://edition.cnn.com/2011/TECH/innovation/03/14/pi.tau.math/index.html.
- "Why Tau Trumps Pi". Scientific American. 2014-06-25. http://www.scientificamerican.com/article/let-s-use-tau-it-s-easier-than-pi/.
- "Python 3.7.0 documentation". https://docs.python.org/3/library/math.html.
- "Perl 6". https://docs.perl6.org/language/terms.
- "Processing". https://processing.org/reference/TAU.html.
- "Nim". https://nim-lang.org/docs/math.html.
- Harremoës, Peter. "Bounds on tail probabilities for negative binomial distributions". Kybernetika 52 (6): 943-966. doi:10.14736/kyb-2016-6-0943. https://dx.doi.org/10.14736%2Fkyb-2016-6-0943
- Harremoës, Peter. "Al-Kashi's constant τ". http://www.harremoes.dk/Peter/Undervis/Turnpage/Turnpage1.pdf. Retrieved 20 September 2018.
- "Life of pi in no danger – Experts cold-shoulder campaign to replace with tau". Telegraph India. 2011-06-30. Archived from the original on 13 July 2013. https://web.archive.org/web/20130713084345/http://www.telegraphindia.com/1110630/jsp/nation/story_14178997.jsp.
- Inversive Geometry. Boston, USA; New York, USA: Ginn and Company, reprint: Courier Corporation, Dover Publications. 2014. 0-486-49339-3. ISBN 978-0-486-49339-8. https://books.google.com/books?id=gu8WAgAAQBAJ. Retrieved 2015-10-17.
