Maple is a symbolic and numeric computing environment as well as a multi-paradigm programming language. It covers several areas of technical computing, such as symbolic mathematics, numerical analysis, data processing, visualization, and others. A toolbox, MapleSim, adds functionality for multidomain physical modeling and code generation. Maple's capacity for symbolic computing include those of a general-purpose computer algebra system. For instance, it can manipulate mathematical expressions and find symbolic solutions to certain problems, such as those arising from ordinary and partial differential equations. Maple is developed commercially by the Canadian software company Maplesoft. The name 'Maple' is a reference to the software's Canadian heritage.
- physical modeling
- multi-paradigm
- multidomain
1. Overview
1.1. Core Functionality
Users can enter mathematics in traditional mathematical notation. Custom user interfaces can also be created. There is support for numeric computations, to arbitrary precision, as well as symbolic computation and visualization. Examples of symbolic computations are given below.
Maple incorporates a dynamically typed imperative-style programming language (resembling Pascal), which permits variables of lexical scope.[1] There are also interfaces to other languages (C, C#, Fortran, Java, MATLAB, and Visual Basic), as well as to Microsoft Excel.
Maple supports MathML 2.0, which is a W3C format for representing and interpreting mathematical expressions, including their display in web pages.[2] There is also functionality for converting expressions from traditional mathematical notation to markup suitable for the typesetting system LaTeX.
1.2. Architecture
Maple is based on a small kernel, written in C, which provides the Maple language. Most functionality is provided by libraries, which come from a variety of sources. Most of the libraries are written in the Maple language; these have viewable source code. Many numerical computations are performed by the NAG Numerical Libraries, ATLAS libraries, or GMP libraries.
Different functionality in Maple requires numerical data in different formats. Symbolic expressions are stored in memory as directed acyclic graphs. The standard interface and calculator interface are written in Java.
2. History
The first concept of Maple arose from a meeting in late 1980 at the University of Waterloo.[3] Researchers at the university wished to purchase a computer powerful enough to run the Lisp-based computer algebra system Macsyma. Instead, they opted to develop their own computer algebra system, named Maple, that would run on lower cost computers. Aiming for portability, they began writing Maple in programming languages from the BCPL family (initially using a subset of B and C, and later on only C).[3] A first limited version appeared after three weeks, and fuller versions entered mainstream use beginning in 1982.[4] By the end of 1983, over 50 universities had copies of Maple installed on their machines.
In 1984, the research group arranged with Watcom Products Inc to license and distribute the first commercially available version, Maple 3.3.[4] In 1988 Waterloo Maple Inc. (Maplesoft) was founded. The company’s original goal was to manage the distribution of the software, but eventually it grew to have its own R&D department, where most of Maple's development takes place today (the remainder being done at various university laboratories[5]).
In 1989, the first graphical user interface for Maple was developed and included with version 4.3 for the Macintosh. X11 and Windows versions of the new interface followed in 1990 with Maple V. In 1992, Maple V Release 2 introduced the Maple "worksheet" that combined text, graphics, and input and typeset output.[6] In 1994 a special issue of a newsletter created by Maple developers called MapleTech was published.[7]
In 1999, with the release of Maple 6, Maple included some of the NAG Numerical Libraries.[8] In 2003, the current "standard" interface was introduced with Maple 9. This interface is primarily written in Java (although portions, such as the rules for typesetting mathematical formulae, are written in the Maple language). The Java interface was criticized for being slow;[9] improvements have been made in later versions, although the Maple 11 documentation[10] recommends the previous ("classic") interface for users with less than 500 MB of physical memory.
Between 1995 and 2005 Maple lost significant market share to competitors due to a weaker user interface.[11] With Maple 10 in 2005, Maple introduced a new "document mode" interface, which has since been further developed across several releases.
In September 2009 Maple and Maplesoft were acquired by the Japanese software retailer Cybernet Systems.[12]
3. Version History
- Maple 1.0: January, 1982
- Maple 1.1: January, 1982
- Maple 2.0: May, 1982
- Maple 2.1: June, 1982
- Maple 2.15: August, 1982
- Maple 2.2: December, 1982
- Maple 3.0: May, 1983
- Maple 3.1: October, 1983
- Maple 3.2: April, 1984
- Maple 3.3: March, 1985 (first public available version)
- Maple 4.0: April, 1986
- Maple 4.1: May, 1987
- Maple 4.2: December, 1987
- Maple 4.3: March, 1989
- Maple V: August, 1990
- Maple V R2: November 1992
- Maple V R3: March 15, 1994
- Maple V R4: January, 1996
- Maple V R5: November 1, 1997
- Maple 6: December 6, 1999
- Maple 7: July 1, 2001
- Maple 8: April 16, 2002
- Maple 9: June 30, 2003
- Maple 9.5: April 15, 2004
- Maple 10: May 10, 2005
- Maple 11: February 21, 2007
- Maple 11.01: July, 2007
- Maple 11.02: November, 2007
- Maple 12: May, 2008
- Maple 12.01: October, 2008
- Maple 12.02: December, 2008
- Maple 13: April 28, 2009[13]
- Maple 13.01: July, 2009
- Maple 13.02: October, 2009
- Maple 14: April 29, 2010[14]
- Maple 14.01: October 28, 2010
- Maple 15: April 13, 2011[15]
- Maple 15.01: June 21, 2011
- Maple 16: March 28, 2012[16]
- Maple 16.01: May 16, 2012
- Maple 17: March 13, 2013[17]
- Maple 17.01: July, 2013
- Maple 18: Mar 5, 2014[18]
- Maple 18.01: May, 2014
- Maple 18.01a: July, 2014
- Maple 18.02: Nov, 2014
- Maple 2015.0: Mar 4, 2015[19]
- Maple 2015.1: Nov, 2015
- Maple 2016.0: March 2, 2016[20]
- Maple 2016.1: April 20, 2016
- Maple 2016.1a: April 27, 2016
- Maple 2017.0: May 25, 2017[21]
- Maple 2017.1: June 28, 2017
- Maple 2017.2: August 2, 2017
- Maple 2017.3: October 3, 2017
- Maple 2018.0: March 21, 2018[22]
- Maple 2019.0: March 14, 2019[23]
- Maple 2020.0: March 12, 2020[24]
4. Features
Features of Maple include:[25]
- Support for symbolic and numeric computation with arbitrary precision
- Elementary and special mathematical function libraries
- Complex numbers and interval arithmetic
- Arithmetic, greatest common divisors and factorization for multivariate polynomials over the rationals, finite fields, algebraic number fields, and algebraic function fields
- Limits, series and asymptotic expansions
- Gröbner basis
- Differential Algebra
- Matrix manipulation tools including support for sparse arrays
- Mathematical function graphing and animation tools
- Solvers for systems of equations, diophantine equations, ODEs, PDEs, DAEs, DDEs and recurrence relations
- Numeric and symbolic tools for discrete and continuous calculus including definite and indefinite integration, definite and indefinite summation, automatic differentiation and continuous and discrete integral transforms
- Constrained and unconstrained local and global optimization
- Statistics including model fitting, hypothesis testing, and probability distributions
- Tools for data manipulation, visualization and analysis
- Tools for probability and combinatoric problems
- Support for time-series and unit based data
- Connection to online collection of financial and economic data
- Tools for financial calculations including bonds, annuities, derivatives, options etc.
- Calculations and simulations on random processes
- Tools for text mining including regular expressions
- Tools for signal processing and linear and non-linear control systems
- Discrete math tools including number theory
- Tools for visualizing and analysing directed and undirected graphs
- Group theory including permutation and finitely presented groups
- Symbolic tensor functions
- Import and export filters for data, image, sound, CAD, and document formats
- Technical word processing including formula editing
- Programming language supporting procedural, functional and object-oriented constructs
- Tools for adding user interfaces to calculations and applications
- Tools for connecting to SQL, Java, .NET, C++, Fortran and http
- Tools for generating code for C, C#, Fortran, Java, JavaScript, Julia, Matlab, Perl, Python, R, and Visual Basic
- Tools for parallel programming
5. Examples of Maple Code
The following code, which computes the factorial of a nonnegative integer, is an example of an imperative programming construct within Maple:
myfac := proc(n::nonnegint) local out, i; out := 1; for i from 2 to n do out := out * i end do; out end proc;
Simple functions can also be defined using the "maps to" arrow notation:
myfac := n -> product(i, i = 1..n);
5.1. Integration
Find
- [math]\displaystyle{ \int\cos\left(\frac{x}{a}\right)dx }[/math].
int(cos(x/a), x);
Output:
- [math]\displaystyle{ a \sin\left(\frac{x}{a}\right) }[/math]
5.2. Determinant
Compute the determinant of a matrix.
M := Matrix(1,2,3], [a,b,c], [x,y,z); # example Matrix
- [math]\displaystyle{ \begin{bmatrix} 1 & 2 & 3 \\ a & b & c \\ x & y & z \end{bmatrix} }[/math]
LinearAlgebra:-Determinant(M);
- [math]\displaystyle{ bz-cy+3ay-2az+2xc-3xb }[/math]
5.3. Series Expansion
series(tanh(x), x = 0, 15)
- [math]\displaystyle{ x-\frac{1}{3}\,x^3+\frac{2}{15}\,x^5-\frac{17}{315}\,x^7 }[/math]
- [math]\displaystyle{ {}+\frac{62}{2835}\,x^9-\frac{1382}{155925}\,x^{11}+\frac{21844}{6081075}\,x^{13}+\mathcal{O}\left(x^{15}\right) }[/math]
5.4. Solve Equations Numerically
The following code numerically calculates the roots of a high-order polynomial:
f := x^53-88*x^5-3*x-5 = 0 fsolve(f) -1.097486315, -.5226535640, 1.099074017
The same command can also solve systems of equations:
f := (cos(x+y))^2 + exp(x)*y+cot(x-y)+cosh(z+x) = 0: g := x^5 - 8*y = 2: h := x+3*y-77*z=55; fsolve( {f,g,h} ); {x = -2.080507182, y = -5.122547821, z = -0.9408850733}
5.5. Plotting of Function of Single Variable
Plot [math]\displaystyle{ x \sin(x) }[/math] with [math]\displaystyle{ x }[/math] ranging from -10 to 10:
plot(x*sin(x), x = -10..10);
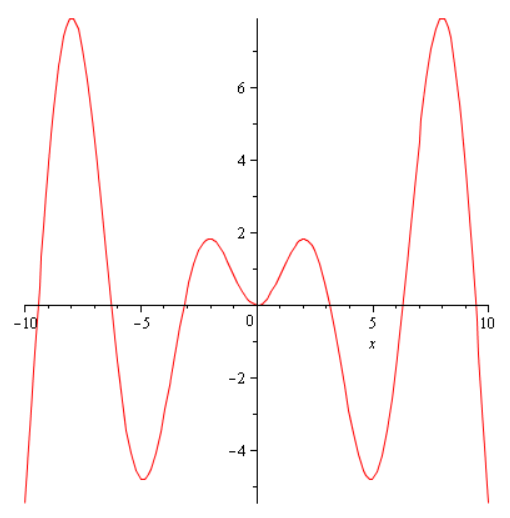
Maple1DPlot. https://handwiki.org/wiki/index.php?curid=1426455
5.6. Plotting of Function of Two Variables
Plot [math]\displaystyle{ x^2+y^2 }[/math] with [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] ranging from -1 to 1:
plot3d(x^2+y^2, x = -1..1, y = -1..1);
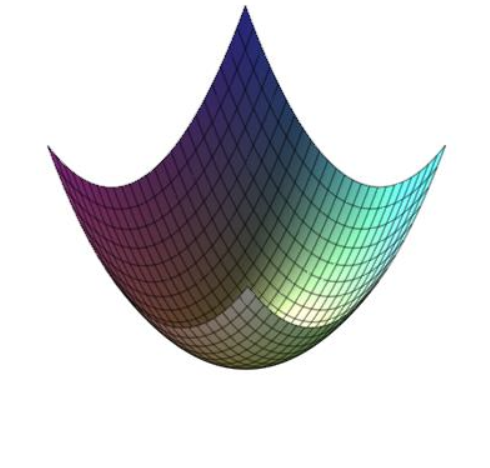
Maple163DPlot. https://handwiki.org/wiki/index.php?curid=1615321
5.7. Animation of Functions
- Animation of function of two variables
- [math]\displaystyle{ f := \frac{2k^2}{\cosh^2\left(x k - 4 k^3 t\right)} }[/math]
plots:-animate(subs(k = 0.5, f), x=-30..30, t=-10..10, numpoints=200, frames=50, color=red, thickness=3);
- Animation of functions of three variables
plots:-animate3d(cos(t*x)*sin(3*t*y), x=-Pi..Pi, y=-Pi..Pi, t=1..2);
- Fly-through animation of 3-D plots.[26]
M := Matrix(400,400,200], [100,100,-400], [1,1,1, datatype=float[8]): plot3d(1, x=0..2*Pi, y=0..Pi, axes=none, coords=spherical, viewpoint=[path=M]);
5.8. Laplace Transform
- Laplace transform
f := (1+A*t+B*t^2)*exp(c*t);
- [math]\displaystyle{ \left(1 + A \, t + B \, t^2\right) e^{c t} }[/math]
inttrans:-laplace(f, t, s);
- [math]\displaystyle{ \frac{1}{s-c}+\frac{A}{(s-c)^2}+\frac{2B}{(s-c)^3} }[/math]
- inverse Laplace transform
inttrans:-invlaplace(1/(s-a), s, x);
- [math]\displaystyle{ e^{ax} }[/math]
5.9. Fourier Transform
- Fourier transform
inttrans:-fourier(sin(x), x, w)
- [math]\displaystyle{ \mathrm{I}\pi\,(\mathrm{Dirac}(w+1)-\mathrm{Dirac}(w-1)) }[/math]
5.10. Integral Equations
Find functions [math]\displaystyle{ f }[/math] that satisfy the integral equation
- [math]\displaystyle{ f(x)-3\int_{-1}^1(xy+x^2y^2)f(y)dy = h(x) }[/math].
eqn:= f(x)-3*Int((x*y+x^2*y^2)*f(y), y=-1..1) = h(x): intsolve(eqn,f(x));
- [math]\displaystyle{ f \left( x \right) =\int _{-1}^{1}\! \left( -15\,{x}^{2}{y}^{2}-3\,xy \right) h \left( y \right) {dy}+h \left( x \right) }[/math]
6. Use of the Maple Engine
The Maple engine is used within several other products from Maplesoft:
- Moebius, DigitalEd’s online testing suite, uses Maple to algorithmically generate questions and grade student responses.
- MapleNet allows users to create JSP pages and Java Applets. MapleNet 12 and above also allow users to upload and work with Maple worksheets containing interactive components.
- MapleSim, an engineering simulation tool.[27]
- Maple Quantum Chemistry Package from RDMChem computes and visualizes the electronic energies and properties of molecules.[28]
Listed below are third-party commercial products that no longer use the Maple engine:
- Versions of Mathcad released between 1994 and 2006 included a Maple-derived algebra engine (MKM, aka Mathsoft Kernel Maple), though subsequent versions use MuPAD.
- Symbolic Math Toolbox in MATLAB contained a portion of the Maple 10 engine, but now uses MuPAD (starting with MATLAB R2007b+ release).[29]
- Older versions of the mathematical editor Scientific Workplace included Maple as a computational engine, though current versions include MuPAD.
The content is sourced from: https://handwiki.org/wiki/Software:Maple
References
- Power of two Bitwise Magazine http://www.bitwisemag.com/copy/reviews/software/maths/maple10_mathematica52.html
- "Welcome to the Maplesoft MathML Home Page". http://www.maplesoft.com/standards/MathML/info.html.
- MacCallum, Malcolm A. H. (2018). "Computer algebra in gravity research". Living Reviews in Relativity 21 (1): 6. doi:10.1007/s41114-018-0015-6. ISSN 2367-3613. PMID 30174551. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=6105178
- "History of Maple". 1998-12-15. http://zakuski.math.utsa.edu/~gokhman/ftp/mirrors/maple/mplhist.htm.
- Two such university labs are the Symbolic Computation Group at the University of Waterloo and the Ontario Research Centre for Computer Algebra at the University of Western Ontario https://www.scg.uwaterloo.ca/
- Maple V Release 2 Notes Maplesoft http://www.maplesoft.com/support/help/Maple/view.aspx?path=updates/v52
- "MTN Special Issue 1994". http://web.mit.edu/maple/www/plibrary/mtn/mtn-si94.html.
- Maple 6.0 Macworld, Feb 2001 http://www.macworld.com/article/1870/2001/02/21reviewsmaple.html
- Capturing knowledge with pure maths, Scientific Computing World. http://www.scientific-computing.com/scwoctnov05review.html
- Maple 11 Installation Guide Maplesoft http://www.maplesoft.com/documentation_center/maple11/Install.html
- Interview with Gaston Gonnet, co-creator of Maple , SIAM History of Numerical Analysis and Computing, 16 March 2005 http://history.siam.org/oralhistories/gonnet.htm
- "Maplesoft Media Releases". https://www.maplesoft.com/company/news/releases/2009/2009-07-30-cybernet-systems-co-ltd-to-acquire-maple.aspx.
- "MaplePrimes Blog - Maple 13 and MapleSim 2 now available". https://www.mapleprimes.com/posts/37445-Maple-13-And-MapleSim-2-Now-Available.
- "MaplePrimes Blog - Announcing Maple 14 and MapleSim 4". https://www.mapleprimes.com/posts/80867-Announcing-Maple-14-And-MapleSim-4-.
- "MaplePrimes Blog - Introducing Maple 15". https://www.mapleprimes.com/maplesoftblog/103907-Introducing-Maple-15.
- "MaplePrimes Blog - Maple 16 is here". https://www.mapleprimes.com/maplesoftblog/132249-Maple-16-Is-Here.
- "MaplePrimes Blog - Introducing Maple 17". https://www.mapleprimes.com/maplesoftblog/144580-Introducing-Maple-17.
- "MaplePrimes Blog - Announcing Maple 18". https://www.mapleprimes.com/maplesoftblog/200200-Announcing-Maple-18.
- "MaplePrimes Blog - Maple 2015 is now available!". https://www.mapleprimes.com/maplesoftblog/200713-Maple-2015-Is-Now-Available.
- "MaplePrimes Blog - Announcing Maple 2016". https://www.mapleprimes.com/maplesoftblog/202794-Announcing-Maple-2016.
- "MaplePrimes Blog - Announcing Maple 2017". https://www.mapleprimes.com/maplesoftblog/208276-Announcing-Maple-2017.
- "MaplePrimes Blog - Maple 2018 is here!". https://www.mapleprimes.com/maplesoftblog/209095-Maple-2018-Is-Here-.
- "MaplePrimes Blog - Announcing Maple 2019". https://www.mapleprimes.com/maplesoftblog/210286-Announcing-Maple-2019.
- "MaplePrimes Blog - Maple 2020 has launched!". https://www.mapleprimes.com/maplesoftblog/212086-Maple-2020-Has-Launched.
- "What is Maple: Product Features - Math & Engineering Software - Maplesoft". https://www.maplesoft.com/products/Maple/features/.
- Using the New Fly-through Feature in Maple 13 Maplesoft http://www.maplesoft.com/applications/view.aspx?SID=33073&view=html
- Mahmud, Khizir; Town, Graham E. (June 2016). "A review of computer tools for modeling electric vehicle energy requirements and their impact on power distribution networks". Applied Energy 172: 337–359. doi:10.1016/j.apenergy.2016.03.100. https://dx.doi.org/10.1016%2Fj.apenergy.2016.03.100
- "MaplePrimes Blog - Introducing the Maple Quantum Chemistry Toolbox". https://www.mapleprimes.com/maplesoftblog/210517-Introducing-The-Maple-Quantum-Chemistry-Toolbox.
- "Release Notes for Symbolic Math Toolbox". MathWorks. http://www.mathworks.com/help/symbolic/release-notes.html#brqy3xk.
