Many concepts in one–dimensional signal processing are similar to concepts in multidimensional signal processing. However, many familiar one–dimensional procedures do not readily generalize to the multidimensional case and some important issues associated with multidimensional signals and systems do not appear in the one–dimensional special case.
- multidimensional
- one–dimensional
- signal processing
1. Motivation and Applications
Most of the signals we witness in real life exist in more than one dimension, be they image, video or sound among many others. A multidimensional (M-D) signal can be modeled as a function of [math]\displaystyle{ M }[/math] independent variables, where [math]\displaystyle{ M }[/math] is greater than or equal to 2. Certain concepts for multidimensional signal processing vary from one dimensional signal processing. For example, The computational complexity for multi-dimensional case is higher as it involves more dimensions. Also, assumptions of causality do not hold good for the multi-dimensional case.
A multidimensional (M-D) signal can be modeled as a function of [math]\displaystyle{ M }[/math] independent variables, where [math]\displaystyle{ M }[/math] is greater than or equal to 2. These signals may be categorized as continuous, discrete, or mixed. A continuous signal can be modeled as a function of independent variables which range over a continuum of values, example – an audio wave traveling in space.A continuous signal in the multi-dimensional case can be represented in the time domain as [math]\displaystyle{ x(t_1,t_2,...t_M) }[/math].The number of arguments within the parenthesis indicates the number of dimensions of the signal. The signal in this case is of n dimensions. A discrete signal, on the other hand, can be modeled as a function defined only on a set of points, such as the set of integers.A discrete signal of [math]\displaystyle{ M }[/math]-dimensions can be represented in the spatial domain as [math]\displaystyle{ x(n_1,n_2,...n_M) }[/math]. A mixed signal is a multidimensional signal that is modeled as a function of some continuous variables and some discrete ones, for example an ensemble of time waveforms recorded from an array of electrical transducers is a mixed signal. The ensemble can be modeled with one continuous variable, time, and one or more discrete variables to index the transducers.
Filtering is an application that is performed on signals whenever certain frequencies are to be removed so as to suppress interfering signals and reduce background noise. A mixed filter is a kind of filter that is different from the traditional Finite Impulse Response(FIR) and Infinite impulse response(IIR) filters and these three filters are explained here in detail. We can combine the M-D Discrete Fourier transform(DFT) method and the M-D linear difference equation(LDE) method to filter the M-D signals. This results in the so-called combined DFT/LDE filtering technique in which the Discrete Fourier Transform is performed in some of the dimensions prior to Linear Difference Equation filtering which is performed later in the remaining dimensions. Such kind of filtering of M-D signals is referred to as Mixed domain(MixeD) filtering and the filters that perform such kind of filtering are referred to as MixeD Multidimensional Filters.[1]
Combining Discrete Transforms with Linear Difference Equations for implementing the Multidimensional filters proves to be computationally efficient and straightforward to design with low memory requirements for spatio-temporal applications such as video processing. Also the Linear Difference equations of the MixeD filters are of lower dimensionality as compared to normal multidimensional filters which results in simplification of the design and increase in the stability.[2]
Multidimensional Digital filters are finding applications in many fields such as image processing, video processing, seismic tomography, magnetic data processing, Computed tomography (CT), RADAR, Sonar and many more.[3] There is a difference between 1-D and M-D digital filter design problems. In the 1-D case, the filter design and filter implementation issues are distinct and decoupled. The 1-D filter can first be designed and then particular network structure can be determined through the appropriate manipulation of the transfer function. In the case of M-D filter design, the multidimensional polynomials cannot be factored in general. This means that an arbitrary transfer function can generally not be manipulated into a form required by a particular implementation. This makes the design and implementation of M-D filters more complex than the 1-D filters.
2. Problem Statement and Basic Concepts[4]
Multidimensional filters not unlike their one dimensional counterparts can be categorized as
- Finite impulse response filters
- Infinite impulse response filters
- Mixed filters
In order to understand these concepts, it is necessary to understand what an impulse response means. An impulse response is basically the response of the system when the input to that system is a Unit impulse function. An impulse response in the spatial domain can be represented as [math]\displaystyle{ h(n_1,n_2,....n_n) }[/math].
A Finite Impulse Response (FIR), or non-recursive filter has an impulse response with a finite number of non-zero samples. This makes their impulse response always absolutely summable and thus FIR filters are always stable. [math]\displaystyle{ x\left(\underline {n}\right) }[/math] is the multidimensional input signal and [math]\displaystyle{ y\left(\underline {n}\right) }[/math] is the multidimensional output signal. For a [math]\displaystyle{ m }[/math] dimensional spatial domain, the output [math]\displaystyle{ y }[/math] can be represented as
[math]\displaystyle{ y\left(n_1,n_2,...,n_m\right)=\sum_{l_1=0}^{L_1-1}\sum_{l_2=0}^{L_2-1}...\sum_{l_m=0}^{L_m-1}a(l_1,l_2,...,l_m)x(n_1-l_1,n_2-l_2,...,n_m-l_m) }[/math]
The above difference equation can be represented in the Z-domain as follows
[math]\displaystyle{ Y(z_1,z_2,....z_m)=\sum_{l_1=0}^{L_1-1}\sum_{l_2=0}^{L_2-1}...\sum_{l_m=0}^{L_m-1}a(l_1,l_2,....l_m)X(z_1,z_2,...z_m)z_1^{-l_1}z_2^{-l_2}......z_m^{-l_m} }[/math],
where [math]\displaystyle{ X(z_1,z_2,...z_m) }[/math] and [math]\displaystyle{ Y(z_1,z_2,....z_m) }[/math] are the Z-transform of [math]\displaystyle{ x(n_1,n_2,...n_m) }[/math], and [math]\displaystyle{ y(n_1,n_2,...n_m) }[/math] respectively.
The transfer function [math]\displaystyle{ H(z_1,z_2,...z_m) }[/math] is given by,
[math]\displaystyle{ H(z_1,z_2,....z_m)=Y(z_1,z_2,...z_m)/X(z_1,z_2,....z_m) }[/math]
In the case of FIR filters the transfer function consists of only numerator terms as the denominator is unity due to the absence of feedback.
An Infinite Impulse Response (IIR), or recursive filter (due to feedback) has infinite-extent impulse response. Its input and output satisfy a multidimensional difference equation of finite order. IIR filters may or may not be stable and in many cases are less complex to realize when compared to FIR filters. The promise of IIR filters is a potential reduction in computation compared to FIR filters when performing comparable filtering operations. by, feeding back output samples, we can use a filter with fewer coefficients (hence less computations) to implement a desired operation. On the other hand, IIR filters pose some potentially significant implementation and stabilization problems not encountered with FIR filters. The design of an M-D recursive filter is quite different from the design of a 1-D filter which is due to the increased difficulty of assuring stability. For a [math]\displaystyle{ m }[/math] dimensional domain, the output [math]\displaystyle{ y }[/math] can be represented as
The transfer function in this case will have both numerator and denominator terms due to the presence of feedback.
Although multidimensional difference equations represent a generalization of 1-D difference equations, they are considerably more complex and quite different. A number of important issues associated with multidimensional difference equations, such as the direction of recursion and the ordering relation, are really not an issue in the 1-D case. Other issues such as stability, although present in the 1-D case, are far more difficult to understand for multidimensional systems
Multidimensional(M-D) filtering may also be achieved by carrying out the P-dimensional Discrete Fourier transform (DFT) over P of the dimensions where (P<M) and spatio-temporal (M - P) dimensional Linear Difference Equation (LDE) filtering over the remaining dimensions. This is referred to as the combined DFT/LDE method. Such an implementation is referred to as mixed filter implementation. Instead of using Discrete Fourier Transform(DFT), other transforms such as Discrete Cosine Transform(DCT) and Discrete Hartley Transform(DHT) can also be used, depending on the application. The Discrete Cosine Transform(DCT) is often preferred for the transform coding of images because of its superior energy-compaction property while Discrete Hartley Transform(DHT) is useful when a real-valued sequence is to be mapped onto a real-valued spectrum.[2]
In general, the M-D Linear Difference Equation (LDE) filter method convolves a real M-D input sequence x(n(M)) with a M-D unit impulse sequence h(n(M))to obtain a desired M-D output sequence y(n(M)).
y(n(M)) = x(n(M)) [math]\displaystyle{ * \overset{M}{\cdots} * }[/math] h(n(M)),
where [math]\displaystyle{ * \overset{M}{\cdots} * }[/math] refers to the M-D convolutional(convolution) operator and (n(M)) refers to the M-D signal domain index vector.
If a sequence is zero for some i and for all [math]\displaystyle{ n_i }[/math] > [math]\displaystyle{ L_i }[/math], where [math]\displaystyle{ L_i \lt }[/math] [math]\displaystyle{ \infty }[/math], that sequence is said to be duration bounded in the ith dimension. A multiplicative operator (R(M)) may be used to obtain from (x(M)) a M-D sequence that is duration bounded. An M-D sequence, [math]\displaystyle{ \bar x \ }[/math](n(M)) = x(n(M))R(n(M)) is duration bounded in the first P dimensions if R(n(M)) = 1 [math]\displaystyle{ \forall }[/math] r(P) where r(P) [math]\displaystyle{ \subset }[/math] n(M) and [math]\displaystyle{ r_i }[/math] [math]\displaystyle{ \leq }[/math] [math]\displaystyle{ L_i \lt }[/math] [math]\displaystyle{ \infty }[/math], i = 1,2,3....P where P [math]\displaystyle{ \leq }[/math] M and 0 otherwise .
The MixeD filter method requires that the M-D input sequence be duration bounded in P of the M dimensions. The index (n(M)) is then ordered so that [math]\displaystyle{ \left(n_1,n_2,...,n_p\right) }[/math] corresponds to the duration-bounded dimensions. The MixeD filtering method involves a P-dimensional(P-D) discrete forward transform operation F(k(P))[.] on [math]\displaystyle{ \bar x \ }[/math](n(M)) over the first P variables [math]\displaystyle{ \left(n_1,n_2,...,n_p\right) }[/math] , which we can write as X(k(P),n(M-P)) = F(k(P))[[math]\displaystyle{ \bar x \ }[/math](n(M))]. Examples of F(k(P))[.] are the P-Dimensional DFT, DCT and DHT. According to the MixeD filter method, each complex sequence, X(k(P),n(M-P)) is filtered by a (M - P)-dimensional LDE. The LDE filters have impulse responses h(k(P),n(M-P)). Finally the complex output sequences of the LDE filters, i.e. Y(k(P),n(M-P)) are inverse transformed using the operator F−1(k(P))[.], to give the final M-D filtered output signal, [math]\displaystyle{ \bar y \ }[/math](n(M)).
The three step process can be summarized as follows,[1]
Step 1. X(k(P),n(M-P)) = F(k(P))[[math]\displaystyle{ \bar x \ }[/math](n(M))]
Step 2. Y(k(P),n(M-P)) = X(k(P),n(M-P)) [math]\displaystyle{ * \overset{M-P}{\cdots} * }[/math] h(k(P),n(M-P))
Step 3. [math]\displaystyle{ \bar y \ }[/math](n(M)) = F−1(k(P))[Y(k(P),n(M-P))]
The crucial step in the MixeD filter design is the 2nd step. This is because filtering takes place in this step. Since there is no filtering involved in Steps 1 and 3, there is no need to weigh the transform coefficients.
The block diagram which shows the MixeD filter method can be seen below.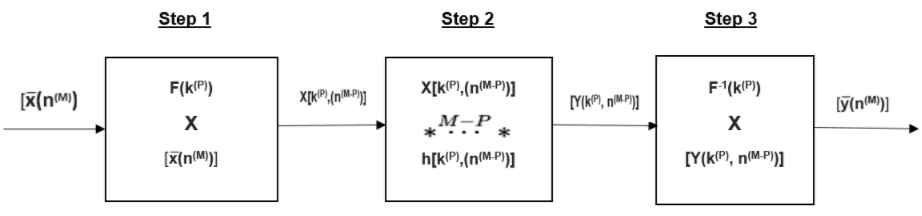
Block diagram showing the MixeD Filter Method. https://handwiki.org/wiki/index.php?curid=1579036
3. FIR Filter Implementation
3.1. Direct Convolution
Output of any Linear Shift Invariant (LSI) filter can be determined from its input by means of the convolution sum. There are a finite number of non-zero samples and the limits of summation are finite for a FIR filter. The convolution sum serves as an algorithm that enables us to compute the successive output samples of the filter. As an example, let is assume that the filter has support over the region {([math]\displaystyle{ n_1 }[/math],[math]\displaystyle{ n_2 }[/math],...,[math]\displaystyle{ n_m }[/math]): [math]\displaystyle{ 0 }[/math] ≤ [math]\displaystyle{ n_1 }[/math] < [math]\displaystyle{ N_1 }[/math] , [math]\displaystyle{ 0 }[/math] ≤ [math]\displaystyle{ n_2 }[/math] < [math]\displaystyle{ N_2 }[/math],...,[math]\displaystyle{ 0 }[/math] ≤ [math]\displaystyle{ n_m }[/math] < [math]\displaystyle{ N_m }[/math] }, the output samples can be computed using[4]
[math]\displaystyle{ y\left(n_1,n_2,...,n_m\right)=\sum_{k_1=0}^{N_1-1}\sum_{k_2=0}^{N_2-1}...\sum_{k_m=0}^{N_m-1}h(k_1,k_2,...,k_m)x(n_1-k_1,n_2-k_2,...,n_m-k_m) }[/math]
If all input samples are available, the output samples can be computed in any order or can also be computed simultaneously. However, if only selected samples of the output are desired, only those samples need to be computed. The number of multiplications and additions for one desired output sample is ([math]\displaystyle{ N_1 }[/math].[math]\displaystyle{ N_2 }[/math]...[math]\displaystyle{ N_m }[/math]) and ([math]\displaystyle{ N_1 }[/math].[math]\displaystyle{ N_2 }[/math]...[math]\displaystyle{ N_m }[/math])–[math]\displaystyle{ 1 }[/math] respectively.
For the 2D case, the computation of [math]\displaystyle{ y\left(n_1,n_2\right) }[/math] depends on input samples from ([math]\displaystyle{ N_1 }[/math] – [math]\displaystyle{ 1 }[/math]) previous columns of the input and the ([math]\displaystyle{ N_2 }[/math] – [math]\displaystyle{ 1 }[/math]) previous rows. If the input samples arrive row by row, we need sufficient storage to store [math]\displaystyle{ N_2 }[/math] rows of the input sequence. If the input is available column by column instead, we need to store [math]\displaystyle{ N_1 }[/math] columns of the input. A zero phase filter with a real impulse response satisfies [math]\displaystyle{ h\left(n_1,n_2\right) }[/math] = [math]\displaystyle{ h\left(-n_1, -n_2\right) }[/math], which means that each sample can be paired with another of identical value. In this case we can use the arithmetic distributive law to interchange some of the multiplications and additions, to reduce the number of multiplications necessary to implement the filter, but the number of multiplications is still proportional to the filter order. Specifically, if the region of support for the filter is assumed to be rectangular and centered at the origin, we have
[math]\displaystyle{ y\left(n_1,n_2\right)=\sum_{k_1=-N_1}^{N_1}\sum_{k_2=-N_2}^{N_2}h(k_1,k_2)x(n_1-k_1,n_2-k_2) }[/math]
Using the above equation to implement an FIR filter requires roughly one-half the number of multiplications of an implementation, although both implementations require the same number of additions and the same amount of storage. If the impulse response of an FIR filter possess other symmetries, they can be exploited in a similar fashion to reduce further the number of required multiplications.
3.2. Discrete Fourier Transform Implementations of FIR Filters
The FIR filter can also be implemented by means of the Discrete Fourier transform (DFT). This can be particularly appealing for high-order filters because the various Fast Fourier transform algorithms permit the efficient evaluation of the DFT. The general form of DFT for multidimensional signals can be seen below, where [math]\displaystyle{ N }[/math] is periodicity matrix, [math]\displaystyle{ x(\underline{n}) }[/math] is the multidimensional signal in the space domain, [math]\displaystyle{ X(\underline{k}) }[/math] is the DFT of [math]\displaystyle{ x(\underline{n}) }[/math] in frequency domain, [math]\displaystyle{ I_N }[/math] is a region containing |[math]\displaystyle{ det N }[/math]| samples in [math]\displaystyle{ n }[/math] domain, and [math]\displaystyle{ J_N }[/math] is a region containing |[math]\displaystyle{ det N^T }[/math]| ([math]\displaystyle{ = det N }[/math]) frequency samples.[4]
[math]\displaystyle{ X\left(\underline{k}\right) = \sum_{n \epsilon I_n}x\left(\underline{n}\right)e^{-j\underline{k}^T\left(2\pi \underline{N}^{-1}\right)\underline{n}} }[/math]
Let [math]\displaystyle{ y\left(n_1,n_2,...,n_m\right) }[/math] be the linear convolution of a finite-extent sequence [math]\displaystyle{ x\left(n_1,n_2,...,n_m\right) }[/math] with the impulse response [math]\displaystyle{ h\left(n_1,n_2,...,n_m\right) }[/math] of an FIR filter.
[math]\displaystyle{ y\left(n_1,n_2,...,n_m\right)=x\left(n_1,n_2,...,n_m\right)*h\left(n_1,n_2,...,n_m\right) }[/math]
On computing Fourier Transform of both sides of this expression, we get
[math]\displaystyle{ Y\left(w_1,w_2,...,w_m\right)=X\left(w_1,w_2,...,w_m\right) }[/math][math]\displaystyle{ H\left(w_1,w_2,...,w_m\right) }[/math]
There are many possible definitions of the M-D discrete Fourier transform, and that all of these correspond to sets of samples of the M-D Fourier transform; these DFT's can be used to perform convolutions as long their assumed region of support contains the support for [math]\displaystyle{ y\left(n_1,n_2,...,n_m\right) }[/math]. Let us assume that [math]\displaystyle{ Y\left(w_1,w_2,...,w_m\right) }[/math] is sampled on a [math]\displaystyle{ N_1 }[/math]x[math]\displaystyle{ N_2 }[/math]x...x[math]\displaystyle{ N_m }[/math] rectangular lattice of samples, and let
[math]\displaystyle{ Y\left(k_1,k_2,...,k_m\right)=Y\left(w_1,w_2,...,w_m\right) | w_1=\frac{2\pi k_1}{N_1} ; w_2=\frac{2\pi k_2}{N_2} ;...; w_m=\frac{2\pi k_m}{N_m} }[/math]
Therefore, [math]\displaystyle{ Y\left(k_1,k_2,...,k_m\right)=X\left(k_1,k_2,...,k_m\right) }[/math][math]\displaystyle{ H\left(k_1,k_2,...,k_m\right) }[/math].
To compute ([math]\displaystyle{ N_1 }[/math]x[math]\displaystyle{ N_2 }[/math]x...x[math]\displaystyle{ N_m }[/math])-point DFT's of [math]\displaystyle{ x }[/math] and [math]\displaystyle{ h }[/math] requires that both sequences have their regions of support extended with samples of value zero. If [math]\displaystyle{ \hat y\left(n_1,n_2,...,n_m\right) }[/math] results from the inverse DFT of the product [math]\displaystyle{ X\left(k_1,k_2,...,k_m\right) }[/math].[math]\displaystyle{ H\left(k_1,k_2,...,k_m\right) }[/math] , then [math]\displaystyle{ \hat y\left(n_1,n_2,...,n_m\right) }[/math] will be the circular convolution of [math]\displaystyle{ h\left(n_1,n_2,...,n_m\right) }[/math] and [math]\displaystyle{ x\left(n_1,n_2,...,n_m\right) }[/math]. If [math]\displaystyle{ N_1 }[/math], [math]\displaystyle{ N_2 }[/math],..., [math]\displaystyle{ N_m }[/math] are chosen to be at least equal to the size of [math]\displaystyle{ y\left(n_1,n_2,...,n_m\right) }[/math], then [math]\displaystyle{ \hat y\left(n_1,n_2,...,n_m\right) = y\left(n_1,n_2,...,n_m\right) }[/math]. This implementation technique is efficient with respect to computation, however it is prodigal with respect to storage as this method requires sufficient storage to contain all [math]\displaystyle{ N_1 }[/math]x[math]\displaystyle{ N_2 }[/math]x...x[math]\displaystyle{ N_m }[/math] points of the signal [math]\displaystyle{ x\left(n_1,n_2,...,n_m\right) }[/math]. In addition, we must store the filter response coefficients [math]\displaystyle{ H\left(k_1,k_2,...,k_m\right) }[/math]. By direct convolution the number of rows of the input that needs to be stored depends on the order of the filter. However, with the DFT the whole input must be stored regardless of the filter order.
For the 2D case, and assuming that [math]\displaystyle{ H\left(k_1,k_2\right) }[/math] is pre-computed, the number of real multiplications needed to compute [math]\displaystyle{ y\left(n_1,n_2\right) }[/math] is
[math]\displaystyle{ 2 }[/math]x[math]\displaystyle{ N_1 }[/math]x[math]\displaystyle{ N_2 }[/math]x[math]\displaystyle{ \log _2 }[/math][math]\displaystyle{ N_1 }[/math]x[math]\displaystyle{ N_2 }[/math] [math]\displaystyle{ + }[/math] [math]\displaystyle{ 2 }[/math]x[math]\displaystyle{ N_1 }[/math]x[math]\displaystyle{ N_2 }[/math]; [math]\displaystyle{ N_1 }[/math] and [math]\displaystyle{ N_2 }[/math] are powers of 2
3.3. Block Convolution
The arithmetic complexity of the DFT implementation of an FIR filter is effectively independent of the order of the filter, while the complexity of a direct convolution implementation is proportional to the filter order. So, the convolution implementation would be more efficient for the lower filter order. As, the filter order increases, the DFT implementation would eventually become more efficient.[4]
The problem with the DFT implementation is that it requires a large storage. The block convolution method offers a compromise. With these approaches the convolutions are performed on sections or blocks of data using DFT methods. Limiting the size of these blocks limits the amount of storage required and using transform methods maintains the efficiency of the procedure.
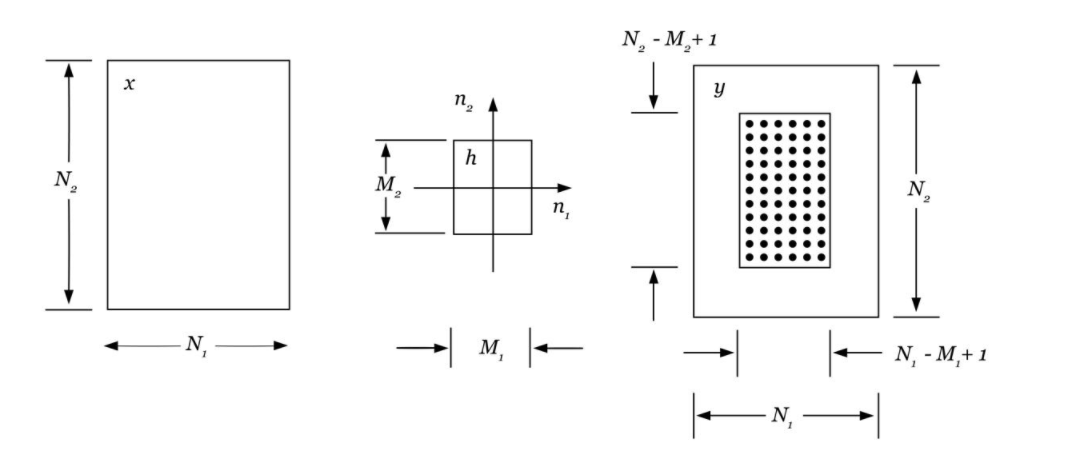
The simplest block convolution method is called the overlap-add technique. We begin by partitioning 2-D array, [math]\displaystyle{ x\left(n_1,n_2\right) }[/math], into ([math]\displaystyle{ N_1 }[/math]x[math]\displaystyle{ N_2 }[/math]) point sections, where the section indexed by the pair ([math]\displaystyle{ k_1 }[/math],[math]\displaystyle{ k_2 }[/math]) is defined as below:
[math]\displaystyle{ x_{k_1k_2}\left(n_1,n_2\right) = x\left(n_1, n_2\right) \text{if } k_1N_1 \le n_1 \lt (k_1 +1)N_1 \text{and } k_2N_2 \le n_2 \lt (k_2 +1)N_2 }[/math]
The regions of support for the different sections do not overlap, and collectively they cover the entire region of support of the array [math]\displaystyle{ x\left(n_1,n_2\right) }[/math]. Thus,
[math]\displaystyle{ x\left(n_1,n_2\right) = \sum_{k_1}\sum_{k_2}x_{k_1k_2}\left(n_1,n_2\right) }[/math]
Because the operation of discrete convolution distributes with respect to addition, [math]\displaystyle{ y\left(n_1,n_2\right) }[/math] can be written as follows:

Screen Shot 2015-11-08 at 4.52.16 PM-01. https://handwiki.org/wiki/index.php?curid=1406318
Figure (a) shows the section of the input array [math]\displaystyle{ x_{21}\left(n_1,n_2\right) }[/math]. Figure (b) shows the region of support of the convolution of that section with [math]\displaystyle{ h }[/math] that is [math]\displaystyle{ y_{21}\left(n_1,n_2\right) }[/math].
The block output [math]\displaystyle{ y_{k_1k_2}\left(n_1,n_2\right) }[/math] is the convolution of [math]\displaystyle{ h\left(n_1,n_2\right) }[/math] with block [math]\displaystyle{ \left(k_1,k_2\right) }[/math] of [math]\displaystyle{ x\left(n_1,n_2\right) }[/math]. The result of the block convolution must be added together to produce the complete filter output [math]\displaystyle{ y\left(n_1,n_2\right) }[/math]. As the support of [math]\displaystyle{ y_{k_1k_2}\left(n_1,n_2\right) }[/math] is greater than the support of [math]\displaystyle{ x_{k_1k_2}\left(n_1,n_2\right) }[/math], the output blocks will of necessity overlap, but the degree of that overlap is limited.
The convolutions of the [math]\displaystyle{ x_{k_1k_2}\left(n_1,n_2\right) }[/math] and [math]\displaystyle{ h(n_1,n_2) }[/math] can be evaluated by means of discrete Fourier transforms, provided that the size of the transform is large enough to support [math]\displaystyle{ y_{k_1k_2}\left(n_1,n_2\right) }[/math]. By controlling the block size we can limit the size of the DFTs, which reduces the required storage.
The overlap-save method is an alternative block convolution technique. When the block size is considerably larger than the support of [math]\displaystyle{ h }[/math], the samples of [math]\displaystyle{ y }[/math] in the center of each block are not overlapped by samples from neighboring blocks. Similarly, when a sequence [math]\displaystyle{ x }[/math] is circularly convolved with another, [math]\displaystyle{ h }[/math], which has a much smaller region of support, only a subset of the samples of that circular convolution will show the effects of the spatial aliasing. The remaining samples of the circular convolution will be identical to the samples of the linear convolution. Thus if an [math]\displaystyle{ (N_1 }[/math]×[math]\displaystyle{ N_2) }[/math] -point section of [math]\displaystyle{ x\left(n_1,n_2\right) }[/math] is circularly convolved with an [math]\displaystyle{ (M_1 }[/math]×[math]\displaystyle{ M_2) }[/math] -point impulse response using an [math]\displaystyle{ (N_1 }[/math]×[math]\displaystyle{ N_2) }[/math] -point DFT, the resulting circular convolution will contain a cluster of [math]\displaystyle{ \left(N_1 - M_1 + 1\right) }[/math] ×[math]\displaystyle{ \left(N_2 - M_2 + 1\right) }[/math] samples which are identical to samples of the linear convolution, [math]\displaystyle{ y }[/math]. The whole output array can be constructed form these "good" samples by carefully choosing the regions of support for the input sections. If the input sections are allowed to overlap, the "good" samples of the various blocks can be made to abut. The overlap-save method thus involves overlapping input sections, whereas the overlap-add method involves overlapping output sections.
Screen Shot 2015-11-11 at 12.52.03 PM-01. https://handwiki.org/wiki/index.php?curid=1839679
The figure above shows the overlap-save method. The shaded region gives those samples of [math]\displaystyle{ y }[/math] for which both the [math]\displaystyle{ (N_1 }[/math]×[math]\displaystyle{ N_2) }[/math] circular convolution and the linear convolution of [math]\displaystyle{ x }[/math] with [math]\displaystyle{ h }[/math] are identical.
For both the overlap-add and overlap-save procedures, the choice of block size affects the efficiency of the resulting implementation. It affects the amount of storage needed, and also affects the amount of computation.
4. FIR Filter Design
4.1. Minimax Design of FIR Filters
The frequency response of a multi-dimensional filter is given by,
[math]\displaystyle{ H(w_1,w_2,...w_n)=\sum_{n_1=0}^{N_1-1}\sum_{n_2=0}^{N_2-1}...\sum_{n_n=0}^{N_n-1} h(n_1,n_2,....n_n)e^{-jw_1n_1}e^{-jw_2n_2}.....e^{-jw_nn_n} }[/math]
where [math]\displaystyle{ h(n_1,n_2,....n_n) }[/math] is the impulse response of the designed filter for size [math]\displaystyle{ N_1\times N_2\times.....N_n }[/math]
The frequency response of the ideal filter is given by
[math]\displaystyle{ I(w_1,w_2,...w_n)=\sum_{n_1=-\infty}^{\infty}\sum_{n_2=-\infty}^{\infty}...\sum_{n_n=-\infty}^{\infty} i(n_1,n_2,....n_n)e^{-jw_1n_1}e^{-jw_2n_2}.....e^{-jw_nn_n} }[/math]
where [math]\displaystyle{ i(n_1,n_2,...n_n) }[/math] is the impulse response of the ideal filter.
The error measure is given by subtracting the above two results i.e.
[math]\displaystyle{ E(w_1,w_2,....w_n)=H(w_1,w_2,.....w_n)-I(w_1,w_2,.....w_n) }[/math]
The maximum of this error measure is what needs to be minimized.There are different norms available for minimizing the error namely:
[math]\displaystyle{ L_2 norm }[/math] given by the formula
[math]\displaystyle{ E_2=[1/(2\pi)^n\int\limits_{-\pi}^{\pi}\int\limits_{-\pi}^{\pi}...\int\limits_{-\pi}^{\pi}\left\vert E(w_1,w_2,...w_n) \right\vert^{2}dw_1dw_2...dw_n]^{1/2} }[/math]
[math]\displaystyle{ L_p norm }[/math] given by the formula
[math]\displaystyle{ E_p=[1/(2\pi)^n\int\limits_{-\pi}^{\pi}\int\limits_{-\pi}^{\pi}...\int\limits_{-\pi}^{\pi}\left\vert E(w_1,w_2,...w_n) \right\vert^{p}dw_1dw_2...dw_n]^{1/p} }[/math]
if p =2 we get the [math]\displaystyle{ L_2 norm }[/math] and if p tends to [math]\displaystyle{ \infty }[/math] we get the [math]\displaystyle{ L_\infty }[/math] norm.The [math]\displaystyle{ L_\infty }[/math] norm is given by,
[math]\displaystyle{ E_\infty=\max_{(w_1,w_2,...w_n\isin B)}\left\vert E(w_1,w_2,...w_n) \right\vert }[/math]
When we say minimax design the [math]\displaystyle{ L_\infty }[/math] norm is what comes to mind.
4.2. Design Using Transformation
Another method to design a multidimensional FIR filter is by the transformation from 1-D filters. This method was first developed by McClellan as other methods were time consuming and cumbersome. The first successful implementation was achieved by Mecklenbrauker and Mersereau[5][6] and was later revised by McClellan and Chan.[7] For a zero phase filter the one phase impulse response is given by[4]
[math]\displaystyle{ h(\ \underline{n})=h^*(-\ \underline{n}) }[/math]
where [math]\displaystyle{ h^*(-\ \underline{n}) }[/math] represents the complex conjugate of [math]\displaystyle{ h(\ \underline{n}) }[/math].
Let [math]\displaystyle{ H(\ \underline{w}) }[/math] be the frequency response of [math]\displaystyle{ h(\ \underline{n}) }[/math].Assuming [math]\displaystyle{ h(\ \underline{n}) }[/math] is even,we can write
[math]\displaystyle{ H(w)=\sum_{n=0}^N a_ncos(wn) }[/math]
where [math]\displaystyle{ a_n }[/math] is defined as [math]\displaystyle{ a_n=h(0) }[/math] if n=0 and [math]\displaystyle{ a_n=2h(n) }[/math] if n[math]\displaystyle{ \ne }[/math]0.Also [math]\displaystyle{ cos(wn) }[/math] is a polynomial of degree n known as the Chebyshev polynomial.
The variable is [math]\displaystyle{ cos(w) }[/math] and the polynomial can be represented by [math]\displaystyle{ T_n(cos(w)) }[/math].
Thus [math]\displaystyle{ H(w)=\sum_{n=0}^N a(n)T_n(cos(w)) }[/math] is the required 1-D frequency response in terms of Chebyshev polynomial [math]\displaystyle{ T_n(cos(w)) }[/math].
If we consider [math]\displaystyle{ F(w_1,w_2,...w_n) }[/math] to be a transformation function where[math]\displaystyle{ F(w_1,w_2,...w_n) }[/math] maps to [math]\displaystyle{ cos(w) }[/math],then we get,
[math]\displaystyle{ H(w_1,w_2,....w_n)=\sum_{n=0}^N a_nT_n[F(w_1,w_2,...w_n)] }[/math]
The contours and the symmetry of [math]\displaystyle{ H(w_1,w_2,.....w_n) }[/math] depend on that of [math]\displaystyle{ F(w_1,w_2,....w_n) }[/math]. [math]\displaystyle{ F(w_1,w_2,....w_n) }[/math] is also called the mapping function.
The values of [math]\displaystyle{ H(w_1,w_2,...w_n) }[/math] can be obtained from the values of the 1_D prototype [math]\displaystyle{ H(w) }[/math].
The conditions for choosing the mapping function are
- · It must be a valid frequency response of a md filter
- · It should be real
- · It should lie between -1 and 1.
Considering a two dimensional case to compute the size of [math]\displaystyle{ H(w_1,w_2) }[/math], If the 1-D prototype has size [math]\displaystyle{ (2N+1) }[/math] and the mapping function has size [math]\displaystyle{ (2Q+1)*(2Q+1) }[/math],then the size of the desired [math]\displaystyle{ H(w_1,w_2) }[/math] will be [math]\displaystyle{ (2NQ+1)*(2NQ+1) }[/math]
The main advantages of this method are
- Easy to implement
- ·Easy to understand 1-D concepts
- ·Optimal filter design is possible
4.3. Implementation of Filters Designed Using Transformations
Methods such as Convolution or implementation using the DFT can be used for the implementation of FIR filters. However, for filters of moderate order another method can be used which justifies the design using transformation.Consider the equation for a 2-dimensional case,
[math]\displaystyle{ H(w_1,w_2)=\sum_{n=0}^N a_nT_n[F(w_1,w_2)] }[/math]
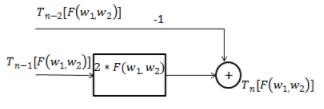
where,[math]\displaystyle{ T_n[F(w_1,w_2)] }[/math] is a Chebyshev polynomial.These polynomials are defined as,
[math]\displaystyle{ T_0[x]=1 }[/math]
[math]\displaystyle{ T_1[x]=x }[/math]
[math]\displaystyle{ T_n[x]=2xT_{n-1}[x]-T_{n-2}[x]. }[/math]
Using this we can form a digital network to realize the 2-D frequency response as shown in the figure below.Replacing x by [math]\displaystyle{ F(w_1,w_2) }[/math] we get,
[math]\displaystyle{ T_n[F(w_1,w_2)]=2F(w_1,w_2)T_{n-1}[F(w_1,w_2)]-T_{n-2}[F(w_1,w_2)] }[/math]
Mdsp rev proj. https://handwiki.org/wiki/index.php?curid=1923010
Since each of these signals can be generated from two lower order signals, a ladder network of N outputs can be formed such that frequency response between the input and nth output is [math]\displaystyle{ T_n[F(w_1,w_2) }[/math] .By weighting these outputs according to the equation mentioned below, The filter [math]\displaystyle{ H(w_1,w_2) }[/math] can be realized.
[math]\displaystyle{ H(w_1,w_2)=\sum_{n=0}^N a_nT_n[F(w_1,w_2)] }[/math]
This realization is as shown in the figure below.
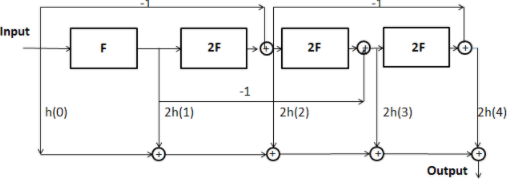
MDSP rev2. https://handwiki.org/wiki/index.php?curid=1933058
In the figure,the filters F define the transformation function and h(n) is the impulse response of the 1-D prototype filter .
4.4. Trigonometric Sum-of-Squares Optimization
Here we discuss a method for multidimensional FIR filter design via sum-of-squares formulations of spectral mask constraints. The sum-of-squares optimization problem is expressed as a semidefinite program with low-rank structure, by sampling the constraints using discrete sine and cosine transforms. The resulting semidefinite program is then solved by a customized primal-dual interior-point method that exploits low-rank structure. This leads to substantial reduction in the computational complexity, compared to general-purpose semidefinite programming methods that exploit sparsity.[8]
A variety of one-dimensional FIR filter design problems can be expressed as convex optimization problems over real trigonometric polynomials, subject to spectral mask constraints. These optimization problems can be formulated as semidefinite programs (SDPs) using classical sum-of-squares (SOS) characterizations of nonnegative polynomials, and solved efficiently via interior-point methods for semidefinite programming.
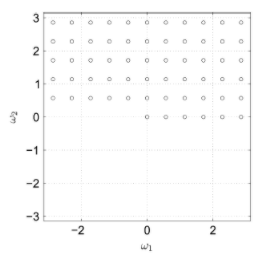
FIR filter in frequency domain with d=2; n1=n2=5 and has 61 sampling points. https://handwiki.org/wiki/index.php?curid=1581306
For the figure above, FIR filter in frequency domain with d=2; n1=n2=5 and has 61 sampling points. The extension of these techniques to multidimensional filter design poses several difficulties. First, SOS characterization of multivariate positive trigonometric polynomials may require factors of arbitrarily high degree. Second, difficulty stems from the large size of the semidefinite programming problems obtained from multivariate SOS programs. Most recent research on exploiting structure in semidefinite programming has focused on exploiting sparsity of the coefficient matrices. This technique is very useful for SDPs derived from SOS programs and are included in several general purpose semidefinite programming packages.
Let [math]\displaystyle{ Z_d }[/math] and [math]\displaystyle{ N_d }[/math] denote the sets of d-vectors of integers and natural numbers, respectively. For a vector [math]\displaystyle{ x }[/math], we define [math]\displaystyle{ diag\left(x\right) }[/math] as the diagonal matrix with [math]\displaystyle{ x_i }[/math] as its ith diagonal entry. For a square matrix [math]\displaystyle{ X }[/math], [math]\displaystyle{ diag\left(X\right) }[/math] is a vector with the [math]\displaystyle{ i^{th} }[/math] entry [math]\displaystyle{ Xii }[/math]. The matrix inequality [math]\displaystyle{ A \gt \ge B }[/math] denotes that [math]\displaystyle{ A-B }[/math] is positive definite (semidefinite). [math]\displaystyle{ Tr\left(A\right) }[/math] denotes the trace of a symmetric matrix [math]\displaystyle{ A }[/math].
[math]\displaystyle{ R }[/math] is a [math]\displaystyle{ d }[/math]-variate trigonometric polynomial of degree [math]\displaystyle{ n \epsilon Z_d }[/math], with real symmetric coefficients [math]\displaystyle{ x_k }[/math] = [math]\displaystyle{ x_{-k} }[/math]
[math]\displaystyle{ R\left(w\right) = \sum_{k =-n}^{n}x_ke^{-jk^Tw} }[/math]
The above summation is over all integer vectors [math]\displaystyle{ k }[/math] that satisfy [math]\displaystyle{ -n \le k \le n }[/math], where the inequalities between the vectors are interpreted element-wise. [math]\displaystyle{ R }[/math] is positive on [math]\displaystyle{ [-\pi , \pi ]^d }[/math], then it can be expressed as sum of squares of trigonometric polynomials
[math]\displaystyle{ H_l\left(w\right) = \sum_{l=1}^{r}|H_l\left(w\right)|^2 }[/math]
[math]\displaystyle{ H_l\left(w\right) = \sum_{k=0}^{n_l}h_{l,k}e^{-jk^Tw} }[/math]
2-D FIR Filter Design as SOS Program: [math]\displaystyle{ H }[/math] is taken to be the frequency response of a 2-D linear phase FIR filter with filter order [math]\displaystyle{ n = \left(n_1, n_2\right) }[/math], with filter coefficients [math]\displaystyle{ h_k }[/math] = [math]\displaystyle{ h_{-k} }[/math].
[math]\displaystyle{ H\left(w\right) = \sum_{k =-n}^{n}h_ke^{-jk^Tw} }[/math]
We want to determine the filter coefficients [math]\displaystyle{ h _k }[/math] that maximize the attenuation [math]\displaystyle{ \delta _s }[/math] in the stopband [math]\displaystyle{ D_s }[/math] for a given maximum allowable ripple ([math]\displaystyle{ \delta _p }[/math]) in the passband [math]\displaystyle{ D_p }[/math]. The optimization problem is to minimize [math]\displaystyle{ \delta _s }[/math] by subjecting to the following conditions
[math]\displaystyle{ |1- H\left(w\right)| \le \delta _p, \, \, w \epsilon D_p }[/math]
[math]\displaystyle{ |H\left(w\right)| \le \delta _s, \, \, w \epsilon D_s }[/math]
where the scalar [math]\displaystyle{ \delta _s }[/math] and the filter coefficients [math]\displaystyle{ h _k }[/math] are the problem variables. These constraints are as shown below
[math]\displaystyle{ R_1\left(w\right) = H\left(w\right)-1+\delta _p \ge 0, \, \, w \epsilon D_p }[/math]
[math]\displaystyle{ R_2\left(w\right) = 1-H\left(w\right)+\delta _p \ge 0, \, \, w \epsilon D_p }[/math]
[math]\displaystyle{ R_3\left(w\right) = H\left(w\right)+\delta _s \ge 0, \, \, w \epsilon D_s }[/math]
[math]\displaystyle{ R_4\left(w\right) = H\left(w\right)-\delta _s \ge 0, \, \, w \epsilon D_s }[/math]
If the passband and stopband are defined, then we can replace each positive polynomial [math]\displaystyle{ R_i }[/math] by a weighted sum of squares expression. Limiting the degrees of the sum-of-squares polynomials to [math]\displaystyle{ n }[/math] then gives sufficient conditions for feasibility. We call the resulting optimization problem a sum-of-squares program and can be solved via semidefinite programming.
5. Iterative Implementation for M-D IIR Filters
In some applications, where access to all values of signal is available (i.e. where entire signal is stored in memory and is available for processing), the concept of "feedback" can be realized. The iterative approach uses the previous output as feedback to generate successively better approximations to the desired output signal.[4]
In general, the IIR frequency response can be expressed as
[math]\displaystyle{ H\left(w_1,w_2,...,w_m\right) = \frac{A\left(w_1,w_2,...,w_m\right)}{B\left(w_1,w_2,...,w_m\right)} = \frac{\sum_{l_1} \sum_{l_2} ... \sum_{l_m} a\left(l_1,l_2,...,l_m\right) e^{-j\left(w_1l_1+w_2l_2+...+w_ml_m\right)}}{\sum_{k_1} \sum_{k_2} ... \sum_{k_m} b\left(k_1,k_2,...,k_m\right) e^{-j\left(w_1k_1+w_2k_2+...+w_mk_m\right)}} }[/math]
where [math]\displaystyle{ a\left(l_1,l_2,...,l_m\right) }[/math] and [math]\displaystyle{ b\left(k_1,k_2,...,k_m\right) }[/math] are M-D finite extent coefficient arrays. The ratio is normalized so that [math]\displaystyle{ b\left(0,0,...,0\right) = 1 }[/math]
Now, let [math]\displaystyle{ X\left(w_1,w_2,...,w_m\right) }[/math] represent the spectrum of a M-D input signal [math]\displaystyle{ x\left(n_1,n_2,...,n_m\right) }[/math] and [math]\displaystyle{ Y\left(w_1,w_2,...,w_m\right) }[/math] represent the spectrum of a M-D output signal [math]\displaystyle{ y\left(n_1,n_2,...,n_m\right) }[/math].
[math]\displaystyle{ Y\left(w_1,w_2,...,w_m\right) = A\left(w_1,w_2,...,w_m\right)X\left(w_1,w_2,...,w_m\right) + C\left(w_1,w_2,...,w_m\right)Y\left(w_1,w_2,...,w_m\right) }[/math]
where [math]\displaystyle{ C\left(w_1,w_2,...,w_m\right) }[/math] is a trigonometric polynomial defined as [math]\displaystyle{ C\left(w_1,w_2,...,w_m\right) = 1- B\left(w_1,w_2,...,w_m\right) }[/math]
In the signal domain, the equation becomes [math]\displaystyle{ y\left(n_1,n_2,...,n_m\right) = a\left(n_1,n_2,...,n_m\right)*x\left(n_1,n_2,...,n_m\right) + c\left(n_1,n_2,...,n_m\right)*y\left(n_1,n_2,...,n_m\right) }[/math]
After making an initial guess, and then substituting the guess in the above equation iteratively, a better approximation of [math]\displaystyle{ y\left(n_1,n_2,...,n_m\right) }[/math] can be obtained – [math]\displaystyle{ y_i\left(n_1,n_2,...,n_m\right)= a\left(n_1,n_2,...,n_m\right)*x\left(n_1,n_2,...,n_m\right) + c\left(n_1,n_2,...,n_m\right)*y_{i-1}\left(n_1,n_2,...,n_m\right) }[/math]
where [math]\displaystyle{ i }[/math] denotes the iteration index
In the frequency domain, the above equation becomes [math]\displaystyle{ Y_i\left(w_1,w_2,...,w_m\right) = A\left(w_1,w_2,...,w_m\right)X\left(w_1,w_2,...,w_m\right) + C\left(w_1,w_2,...,w_m\right)Y_{i-1}\left(w_1,w_2,...,w_m\right) }[/math]
An IIR filter is BIBO stable if [math]\displaystyle{ C\left(w_1,w_2,...,w_m\right) \neq 0 }[/math]
If we assume that [math]\displaystyle{ | C\left(w_1,w_2,...,w_m\right) | \lt 1 }[/math] then
[math]\displaystyle{ \lim_{I \to \infty}Y_I\left(w_1,w_2,...,w_m\right) = \frac{A\left(w_1,w_2,...,w_m\right)X\left(w_1,w_2,...,w_m\right)}{1 - C\left(w_1,w_2,...,w_m\right)} = Y\left(w_1,w_2,...,w_m\right) }[/math]

design. https://handwiki.org/wiki/index.php?curid=1203190
Thus, it can be said that, the frequency response [math]\displaystyle{ H\left(w_1,w_2,...,w_m\right) }[/math] of a M-D IIR filter can be obtained by infinite number of M-D FIR filtering operations. The store operator stores the result of the previous iteration.
To be practical, an iterative IIR filter should require fewer computations, counting all iterations to achieve an acceptable error, compared to an FIR filter with similar performance.
6. Existing Approaches for IIR Filter Design
Similar to its 1-D special case, M-D IIR filters can have dramatically lower order than FIR filters with similar performance. This motivates the development of design techniques for M-D IIR filtering algorithms. This section presents brief overview of approaches for designing M-D IIR filters.
6.1. Shank's Method
This technique is based on minimizing the error functionals in the space domain. The coefficient arrays [math]\displaystyle{ a\left(n_1,n_2,...,n_m\right) }[/math] and [math]\displaystyle{ b\left(n_1,n_2,...,n_m\right) }[/math] are determined such that the output response [math]\displaystyle{ y\left(n_1,n_2\right) }[/math] of a filter matches the desired response [math]\displaystyle{ d\left(n_1,n_2,...,n_m\right) }[/math].[4]
Let us denote the error signal as
[math]\displaystyle{ e\left(n_1,n_2,...,n_m\right) = y\left(n_1,n_2,...,n_m\right) - d\left(n_1,n_2,...,n_m\right) }[/math]
And let [math]\displaystyle{ E\left(w_1,w_2,...,w_m\right) }[/math] denote it's the Fourier transform
[math]\displaystyle{ E\left(w_1,w_2,...,w_m\right) = \frac{A\left(w_1,w_2,...,w_m\right)X\left(w_1,w_2,...,w_m\right)}{B\left(w_1,w_2,...,w_m\right)} - D\left(w_1,w_2,...,w_m\right) }[/math]
By multiplying both sides by [math]\displaystyle{ B\left(w_1,w_2,...,w_m\right) }[/math], we get the modified error spectrum, converted in discrete domain as
[math]\displaystyle{ e'\left(n_1,n_2,...,n_m\right) = a\left(n_1,n_2,...,n_m\right)*x\left(n_1,n_2,...,n_m\right) - b\left(n_1,n_2,...,n_m\right)*d\left(n_1,n_2,...,n_m\right) }[/math]
The total mean-squared error is obtained as
[math]\displaystyle{ e'_2\left(n_1,n_2,...,n_m\right) = \sum_{n_1}\sum_{n_2} ... \sum_{n_m}[e'\left(n_1,n_2,...,n_m\right)]^2 }[/math]
Let the input signal be [math]\displaystyle{ \delta\left(n_1,n_2,...,n_m\right) }[/math]. Now, the numerator coefficient [math]\displaystyle{ a\left(n_1,n_2,...,n_m\right) }[/math] is zero outside region [math]\displaystyle{ 0 \le n_1 \le N_1-1 \, \& \, 0 \le n_2 \le N_2-1 ... , 0 \le n_m \le N_m-1 }[/math] because of the ROS of input signal.Then equation becomes
[math]\displaystyle{ e'\left(n_1,n_2,...,n_m\right) = -\sum_{q_1=0}^{M_1-1}\sum_{q_2=0}^{M_2-1}...\sum_{q_m=0}^{M_m-1}b\left(q_1,q_2,..,q_m\right)d\left(n_1-q_1,n_2-q_2\right)\,;\, }[/math] for [math]\displaystyle{ n_1 \ge N_1-1 }[/math] or [math]\displaystyle{ n_2 \ge N_2-1 }[/math] or ... [math]\displaystyle{ n_m \ge N_m-1 }[/math]
Substituting the result [math]\displaystyle{ e' }[/math] into [math]\displaystyle{ e_2' }[/math] and differentiating [math]\displaystyle{ e'_2 }[/math] with respect to denominator coefficients [math]\displaystyle{ b\left(q_1,q_2,...,q_n\right) }[/math], the linear set of equations is obtained as
[math]\displaystyle{ \sum_{m_1=0}^{M_1-1}\sum_{m_2=0}^{M_2-1}...\sum_{m_m=0}^{M_m-1}b\left(m_1,m_2,...,m_m\right)r\left(m_1,m_2,...,m_m;q_1,q_2,...,q_m\right) = 0 \,;\, }[/math] for [math]\displaystyle{ 0 \le m_1 \lt M_1 ; 0 \le m_2 \lt M_2 ; ... ; 0 \le m_m \lt M_m }[/math]
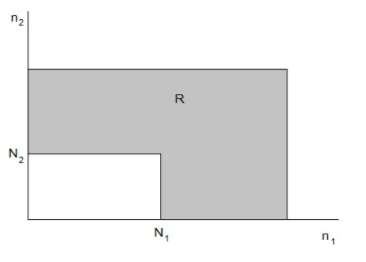
Design. https://handwiki.org/wiki/index.php?curid=1828426
Now, taking the double summation for the region "R" i.e. for [math]\displaystyle{ n_1 \ge N_1-1 }[/math] and [math]\displaystyle{ n_2 \ge N_2-1 }[/math] and ... [math]\displaystyle{ n_m \ge N_m-1 }[/math] shown in figure (shown for 2-D case), the coefficients [math]\displaystyle{ b\left(n_1,n_2,...,n_m\right) }[/math] are obtained.
The coefficients [math]\displaystyle{ a\left(n_1,n_2,...,n_m\right) }[/math] can be obtained from
[math]\displaystyle{ a\left(n_1,n_2,...,n_m\right) \approx b\left(n_1,n_2,...,n_m\right)*d\left(n_1,n_2,...,n_m\right) }[/math]
The major advantage of Shank's method is that IIR filter coefficients can be obtained by solving linear equations. The disadvantage is that the mean squared error between [math]\displaystyle{ y }[/math] and [math]\displaystyle{ d }[/math] is not minimized. Also, the stability is not certain.
7. Frequency-domain Designs for IIR[4]
Shank's method is a spatial-domain design method. It is also possible to design IIR filters in the frequency domain. Here our aim would be to minimize the error in the frequency domain and not the spatial domain.Due to Parseval's theorem we observe that the mean squared error will be identical to that in the spatial domain.Parseval's theorem states that[4]
Also the different norms that are used for FIR filter design such as [math]\displaystyle{ L_2 }[/math],[math]\displaystyle{ L_p }[/math] and [math]\displaystyle{ L_\infty }[/math] can also be used for the design of IIR filters
[math]\displaystyle{ E_p=[1/(2\pi)^n\int\limits_{-\pi}^{\pi}\int\limits_{-\pi}^{\pi}...\int\limits_{-\pi}^{\pi}\left\vert E(w_1,w_2,...w_n) \right\vert^{p}dw_1dw_2...dw_n]^{1/p} }[/math]
is the required equation for the [math]\displaystyle{ L_p }[/math] norm and when p tends to [math]\displaystyle{ \infty }[/math] we get the [math]\displaystyle{ L_\infty }[/math] norm as explained above
[math]\displaystyle{ E_\infty=\max_{(w_1,w_2,...w_n\isin B)}\left\vert E(w_1,w_2,...w_n) \right\vert }[/math]
The main advantages of design in the frequency domain are
- If there is any specification which is only partially complete, such as approximation of a magnitude response without the specification of phase response, this can be implemented with greater ease in the frequency domain rather than the space domain.
- Also the approximating function can be written in closed form as a function of the filter parameters, thus facilitating simpler derivation of partial derivatives.
The main disadvantage of this technique is that there is no guarantee for stability.
General minimization techniques as seen in the design of IIR filters in the spatial domain can be used in the frequency domain too.
One popular method for frequency domain design is the Magnitude and magnitude squared algorithms.
7.1. Magnitude and Magnitude Squared Design Algorithm
In this section, we examine the technique for designing 2-D IIR filters based on minimizing error functionals in the frequency domain. The mean-squared error is given as
[math]\displaystyle{ \frac{1}{\left(2\pi\right) ^m} \int_{-\pi}^{\pi} \int_{-\pi}^{\pi} ... \int_{-\pi}^{\pi}|Y\left(w_1,w_2,...,w_m\right) - D\left(w_1,w_2,...,w_m\right)|^2 dw_1dw_2...dw_m }[/math]
The below function [math]\displaystyle{ J_a }[/math] is the measure of difference between two complex functions - the desired response [math]\displaystyle{ D\left(w_1,w_2,...,w_m\right) }[/math] and the actual response [math]\displaystyle{ Y\left(w_1,w_2,...,w_m\right) }[/math]. Generally, we can define a complex function [math]\displaystyle{ f }[/math] of [math]\displaystyle{ Y }[/math] to approximate the desired response [math]\displaystyle{ D }[/math]. Hence, the optimization task boils down to the task of minimizing [math]\displaystyle{ f (Y)-D }[/math].
[math]\displaystyle{ J_a = \sum_{k}W\left(w_{1k},w_{2k},...,w_{mk}\right)[f\left(\frac{A\left(w_{1k},w_{2k},...,w_{mk}\right)}{B\left(w_{1k},w_{2k},...,w_{mk}\right)} \right) - D\left(w_{1k},w_{2k},...,w_{mk}\right)]^2 }[/math]
where [math]\displaystyle{ W\left(w_1,w_2,...,w_m\right) }[/math] is the weighting function and [math]\displaystyle{ \left(w_{1k},w_{2k},...w_{mk}\right) }[/math] are frequency domain samples selected for minimization. Now, consider a case, where we ignore the phase response of the filter i.e. we concentrate on only matching the magnitude (or square of magnitude) of the desired and actual filter response. Linearization can be used to find out the coefficients [math]\displaystyle{ \{a\left(n_1,n_2,...,w_m\right) \, b\left(n_1,n_2,...,w_m\right)\} }[/math] that results in minimum value of [math]\displaystyle{ J_a }[/math]. This will ensure that the filter form can be represented by a finite order difference equation. The stability of the filter depends on the function[math]\displaystyle{ Y\left(w_1,w_2,...,w_m\right) }[/math].
The disadvantages of this method are,
- Stability cannot be guaranteed
- Depending on the function [math]\displaystyle{ f }[/math], the computations of partial derivatives will be cumbersome.
7.2. Magnitude Design with Stability Constraint
This design procedure includes a stability error [math]\displaystyle{ J_s }[/math], which is to be minimized together with the usual approximation error [math]\displaystyle{ J_a }[/math].[9] The stability error is a crude measure of how unstable a filter is. It is a type of penalty function. It should be zero for stable filters and large for the unstable filters. The filters can be designed by minimizing[4]
[math]\displaystyle{ J = J_a + aJ_s }[/math]
[math]\displaystyle{ a }[/math] is a positive constraint which weights the relative importance of [math]\displaystyle{ J_a }[/math] and [math]\displaystyle{ J_s }[/math]. Ekstrom et al.[9] used the nonlinear optimization techniques to minimize [math]\displaystyle{ J }[/math]. Their stability error was based on the difference between the denominator coefficient array and the minimum-phase array with the same autocorrelation function.
The minimum phase array can be determined by first computing the autocorrelation function of the denominator coefficient array [math]\displaystyle{ b\left(n_1,n_2\right) }[/math].
[math]\displaystyle{ r_b\left(n_1, n_2\right) = \sum_{q_1}\sum_{q_2}b\left(q_1,q_2\right)b\left(q_1+n_1, q_2+n_2\right) }[/math]
After computing [math]\displaystyle{ r_b }[/math], its Fourier transform [math]\displaystyle{ R_b\left(w_1,w_2\right) }[/math] must be split into its minimum- and maximum-phase components. This is accomplished by spectral factorization using the complex cepstrum.
We form the cepstrum [math]\displaystyle{ r_b\left(n_1, n_2\right) }[/math] of the autocorrelation function is formed and multiplied by a non symmetric half-plane window [math]\displaystyle{ w\left(n_1, n_2\right) }[/math] to obtain the cepstrum,
[math]\displaystyle{ b_{mp}\left(n_1, n_2\right) = r_b\left(n_1, n_2\right)w\left(n_1, n_2\right) }[/math]
The subscript "mp" denotes that this cepstrum corresponds to a minimum phase sequence [math]\displaystyle{ b_{mp}\left(n_1, n_2\right) }[/math].
If the designed filter is stable, its denominator coefficient array [math]\displaystyle{ b(n_1, n_2) }[/math] is a minimum-phase sequence with non symmetric half-plane support. In this case, [math]\displaystyle{ b(n_1, n_2) }[/math] is equal to [math]\displaystyle{ b_{mp}(n_1, n_2) }[/math]; otherwise it is not.
[math]\displaystyle{ J_s }[/math] can be denoted as,
[math]\displaystyle{ J_s = \sum_{n_1}\sum_{n_2}[b(n_1, n_2) - b_{mp}(n_1, n_2)]^2 }[/math]
In practice, [math]\displaystyle{ J_s }[/math] is rarely driven to zero because of numerical errors in computing the cepstrum [math]\displaystyle{ r_b\left(n_1, n_2\right) }[/math]. In general, [math]\displaystyle{ r_b\left(n_1, n_2\right) }[/math] has infinite extent, and spatial aliasing results when the FFT is used to compute it. The degree of aliasing can be controlled by increasing the size of the FFT.
8. Design and Implementation of M-D Zero-phase IIR Filters
Often, especially in applications such as image processing, one may be required to design a filter with symmetric impulse response. Such filters will have a real-valued, or zero-phase, frequency response. Zero-phase IIR filter could be implemented in two ways, cascade or parallel.[4]
- 1. The cascade approach
In the cascade approach, a filter whose impulse response is [math]\displaystyle{ h\left(n_1, n_2\right) }[/math] is cascaded with a filter whose impulse response is [math]\displaystyle{ h\left(-n_1, -n_2\right) }[/math]. The overall impulse response of the cascade is [math]\displaystyle{ h\left(n_1, n_2\right) ** h\left(-n_1, -n_2\right) }[/math]. The overall frequency response is a real and non-negative function,
[math]\displaystyle{ C\left(w_1, w_2\right) = \left\vert H\left(w_1, w_2\right)\right\vert^2 }[/math]
The cascade approach suffers from some computational problems due to transient effects. The output samples of the second filter in the cascade are computed by a recursion which runs in the opposite direction from that of the first filter. For an IIR filter, its output has infinite extent, and theoretically an infinite number of its output samples must be evaluated before filtering with the [math]\displaystyle{ h\left(-n_1, -n_2\right) }[/math] can begin, even if the ultimate output is desired only over a limited region. Truncating the computations from the first filter can introduce errors. As a practical approach, the output form the first filter must be computed far enough out in space depending on the region-of-support of the numerator coefficient array [math]\displaystyle{ a\left(n_1, n_2\right) }[/math] and on the location of the to-be-computed second filter's output sample, so that any initial transient from the second filter will have effectively died out in the region of interest of the final output.
- 2. The parallel approach
In the parallel approach, the outputs of two non symmetric half-plane (OR four non-symmetric quarter-plane) IIR filters are added to form the final output signal. As in the cascade approach, the second filter is a space-reserved version of the first. The overall frequency response is given by,
[math]\displaystyle{ P\left(w_1, w_2 \right) = H\left(w_1, w_2 \right) + H^*\left(w_1, w_2 \right) = 2\text{ Re}[H\left(w_1, w_2 \right)] }[/math]
This approach avoids the problems of the cascade approach for zero-phase implementation. But, this approach is best suited for the 2-D IIR filters designed in the space domain, where the desired filter response [math]\displaystyle{ d\left(n_1, n_2\right) }[/math] can be partitioned into the proper regions of support.
For a symmetric zero-phase 2-D IIR filter, the denominator has a real positive frequency response.
[math]\displaystyle{ H\left(w_1,w_2,...,w_m\right) = \frac{A\left(w_1,w_2,...,w_m\right)}{B\left(w_1,w_2,...,w_m\right)} }[/math]
For 2-D zero-phase IIR filter, since
[math]\displaystyle{ a\left(n_1, n_2\right) = a\left(-n_1, -n_2\right) }[/math]
[math]\displaystyle{ b\left(n_1, n_2\right) = b\left(-n_1, -n_2\right) }[/math]
We can write,
[math]\displaystyle{ A\left(w_1, w_2\right) = \sum_{n_1}\sum_{n_2}a'\left(n_1, n_2\right) cos(w_1n_1 + w_2n_2) }[/math]
[math]\displaystyle{ B\left(w_1, w_2\right) = \sum_{n_1}\sum_{n_2}b'\left(m_1, m_2\right) cos(w_1m_1 + w_2m_2) }[/math]
We can formulate the mean-squared error functional that could be minimized by various techniques. The result of the minimization would yield the zero-phase filter coefficients [math]\displaystyle{ {a'\left(n_1, n_2\right), b'\left(n_1, n_2\right)} }[/math]. We can use these coefficients to implement the designed filter then.
9. Implementation of Mixed Multidimensional Filters
If the M-D transform transfer function, H(n(M)) = Y(n(M))/X(n(M)) for a particular class of inputs x(n(M)) and a particular transform is known, the design approximation problem becomes simple and we then have to find the (M-P) dimensional LDE's, one for each P-tuple that help in approximating all the complex (M-P) dimensional transform transfer functions, H(k(P),k(M-P)). But as the multidimensional approximation theory for dimensions greater than 2 is not well developed, the (M-P) dimensional approximation maybe a problem. The input and output sequences of each (M-P) dimensional LDE are complex and are given by X(k(P),k(M-P)) and Y(k(P),k(M-P)) respectively. The main design objective is to choose coefficients of the LDE in such a way that the complex (M-P) dimensional transform transfer function of the sequences X(k(P),k(M-P)) and Y(k(P),k(M-P)), are approximately in the ratio of H(k(P),k(M-P)) = H(n(M)). This can be very difficult unless certain transforms such as DFT, DCT and DHT are used. For the above-mentioned transforms, it is possible to find the (M-P) dimensional impulse response, h(k(P),n(M-P)) by approximating the Linear Difference Equations.
The following approaches can be used to implement Mixed Multidimensional filters:
9.1. Using Discrete Fourier Transform (DFT)
For a multidimensional array [math]\displaystyle{ x_{n_1, n_2, \dots, n_p} }[/math] that is a function of p discrete variables [math]\displaystyle{ n_\ell = 0, 1, \dots, N_\ell-1 }[/math] for [math]\displaystyle{ \ell }[/math] in [math]\displaystyle{ 1, 2, \dots, p }[/math], the P-Dimensional Discrete Forward Fourier Transform is defined by:
F(k(P)) = [math]\displaystyle{ \sum_{n_1=0}^{N_1-1} \left(\omega_{N_1}^{~k_1 n_1} \sum_{n_2=0}^{N_2-1} \left( \omega_{N_2}^{~k_2 n_2} \cdots \sum_{n_p=0}^{N_p-1} \omega_{N_p}^{~k_p n_p}\cdot x_{n_1, n_2, \dots, n_p} \right) \right) \, , }[/math],
where [math]\displaystyle{ \omega_{N_\ell} = \exp(-2\pi i/N_\ell) }[/math] as shown above and the p output indices run from [math]\displaystyle{ k_\ell = 0, 1, \dots, N_\ell-1 }[/math]. If we want to express it in vector notation, where [math]\displaystyle{ \mathbf{n} = (n_1, n_2, \dots, n_p) }[/math] and [math]\displaystyle{ \mathbf{k} = (k_1, k_2, \dots, k_p) }[/math] are p-dimensional vectors of indices from 0 to [math]\displaystyle{ \mathbf{N} - 1 }[/math], where [math]\displaystyle{ \mathbf{N} - 1 = (N_1 - 1, N_2 - 1, \dots, N_p - 1) }[/math], the P-Dimensional Discrete Forward Fourier Transform is given by :
F(k(P)) = [math]\displaystyle{ \sum_{\mathbf{n}=\mathbf{0}}^{\mathbf{N}-1} e^{-2\pi i \mathbf{k^T} \cdot (\mathbf{n} / \mathbf{N})} x_\mathbf{n} \, , }[/math],
where the division [math]\displaystyle{ \mathbf{n} / \mathbf{N} }[/math] is defined as [math]\displaystyle{ \mathbf{n} / \mathbf{N} = (n_1/N_1, \dots, n_p/N_p) }[/math] to be performed element-wise, and the sum denotes the set of nested summations above.
To find the P-Dimensional inverse Discrete Fourier Transform, we can use the following:
F−1(k(P)) = [math]\displaystyle{ \frac{1}{\prod_{\ell=1}^p N_\ell} \sum_{\mathbf{k}=\mathbf{0}}^{\mathbf{N}-1} e^{2\pi i \mathbf{n} \cdot (\mathbf{k^T} / \mathbf{N})} \,. }[/math] F(k(P)).
The Discrete Fourier Transform is useful for certain applications such as Data Compression, Spectral Analysis, Polynomial Multiplication, etc. The DFT is also used as a building block for techniques that take advantage of properties of signals frequency-domain representation, such as the overlap-save and overlap-add fast convolution algorithms. However the computational complexity increases if Discrete Fourier Transform is used as the Discrete Transform. The computational complexity of the DFT is way higher than the other Discrete Transforms and for P-D DFT, the computational complexity is given by O([math]\displaystyle{ N_1^2 }[/math][math]\displaystyle{ N_2^2 }[/math]...[math]\displaystyle{ N_P^2 }[/math]). Therefore, the Fast Fourier Transform(FFT) is used to compute the DFT as it reduces the computational complexity significantly to O([math]\displaystyle{ N_1 }[/math][math]\displaystyle{ N_2 }[/math]...[math]\displaystyle{ N_P }[/math][math]\displaystyle{ Log_2 }[/math][math]\displaystyle{ N_1 }[/math][math]\displaystyle{ N_2 }[/math]...[math]\displaystyle{ N_P }[/math]) and at the same time other Discrete Transforms are preferred over the DFT.
9.2. Using Discrete Cosine Transform (DCT)
For a multidimensional array [math]\displaystyle{ x_{n_1, n_2, \dots, n_p} }[/math] that is a function of p discrete variables [math]\displaystyle{ n_\ell = 0, 1, \dots, N_\ell-1 }[/math] for [math]\displaystyle{ \ell }[/math] in [math]\displaystyle{ 1, 2, \dots, p }[/math], the P-Dimensional Discrete Forward Cosine Transform is defined by:
F(k(P))
The P-Dimensional inverse Discrete Cosine Transform is given by:
F−1(k(P))
The DCT finds its use in data compression applications such as the JPEG image format. The DCT has high degree of spectral compaction at a qualitative level, which makes it very suitable for various compression applications. A signal's DCT representation tends to have more of its energy concentrated in a small number of coefficients when compared to other transforms like the DFT. Thus you can reduce your data storage requirement by only storing the DCT outputs that contain significant amounts of energy. The computational complexity of P-D DCT goes by O([math]\displaystyle{ N_1 }[/math][math]\displaystyle{ N_2 }[/math]...[math]\displaystyle{ N_P }[/math][math]\displaystyle{ Log_2 }[/math][math]\displaystyle{ N_1 }[/math][math]\displaystyle{ N_2 }[/math]...[math]\displaystyle{ N_P }[/math]). Since the number of operations required to compute the DCT is less than that required to compute the DFT without the use of FFT, the DCT's are also called as Fast Cosine Transforms(FCT).
9.3. Using Discrete Hartley Transform (DHT)
For a multidimensional array [math]\displaystyle{ x_{n_1, n_2, \dots, n_p} }[/math] that is a function of p discrete variables [math]\displaystyle{ n_\ell = 0, 1, \dots, N_\ell-1 }[/math] for [math]\displaystyle{ \ell }[/math] in [math]\displaystyle{ 1, 2, \dots, p }[/math], the P-Dimensional Discrete Forward Hartley Transform is defined by:
F(k(P)) [math]\displaystyle{ =\sum_{n_1=0}^{N_1-1} \sum_{n_2=0}^{N_2-1} \dots \sum_{n_p=0}^{N_p-1} x(n_1,n_2,...,n_p)cas(\frac{2\pi n_1 k_1}{N_1}+\dots +\frac{2\pi n_p k_p}{N_p}), }[/math] where, [math]\displaystyle{ k_i = 0,1,\ldots, N_i-1 }[/math] and where [math]\displaystyle{ cas(x)=cos(x)+sin(x). }[/math]
If Discrete Hartley Transform is used, the computational complexity of complex numbers can be avoided. The overall computational complexity of P-D Discrete Hartley Transform is given by O([math]\displaystyle{ N_1 }[/math][math]\displaystyle{ N_2 }[/math]...[math]\displaystyle{ N_P }[/math][math]\displaystyle{ Log_2 }[/math][math]\displaystyle{ N_1 }[/math][math]\displaystyle{ N_2 }[/math]...[math]\displaystyle{ N_P }[/math]), if algorithms similar to the FFT are used and thus the DHT is also referred to as the Fast Hartley Transform(FHT).
The Discrete Hartley Transform is used in various applications in communications and signal processing areas. Some of these applications include multidimensional filtering, multidimensional spectral analysis, error control coding, adaptive digital filters, image processing etc.
10. Applications of MixeD Multidimensional Filters
Mixed 3-D filters can be used for enhancement of 3-D spatially planar signals. A 3-D MixeD Cone filter can be designed using 2-D DHT and is shown below.
10.1. Review of 3-D Spatially Planar Signals[1]
An M-D signal, x(n(M)) is considered to be spatially-planar(SP) if it is constant on all surfaces, i.e. [math]\displaystyle{ \alpha_1\! }[/math][math]\displaystyle{ n_1 }[/math] + [math]\displaystyle{ \alpha_2\! }[/math][math]\displaystyle{ n_2 }[/math] +[math]\displaystyle{ \cdots }[/math] + [math]\displaystyle{ \alpha_M\! }[/math][math]\displaystyle{ n_M }[/math] = d, for [math]\displaystyle{ \forall }[/math]d [math]\displaystyle{ \in }[/math]R where R is the set of real numbers.
Therefore, a 3-D spatially planar signal, x(n(3)) is constant on 3 surfaces and is given by [math]\displaystyle{ \alpha_1\! }[/math][math]\displaystyle{ n_1 }[/math] + [math]\displaystyle{ \alpha_2\! }[/math][math]\displaystyle{ n_2 }[/math] + [math]\displaystyle{ \alpha_3\! }[/math][math]\displaystyle{ n_3 }[/math] = d, for [math]\displaystyle{ \forall }[/math]d [math]\displaystyle{ \in }[/math]R
It may be shown that the 3-D DFT of a SP x(n(M)) yields 3-D DFT frequency domain coefficients, X(k(3)), which are zero everywhere except on the line L(k(3)) where (k(3)) [math]\displaystyle{ \in }[/math] [math]\displaystyle{ \{ }[/math] Z[math]\displaystyle{ \vert }[/math] [math]\displaystyle{ k_1 }[/math]/[math]\displaystyle{ \alpha_1\! }[/math]=[math]\displaystyle{ k_2 }[/math]/[math]\displaystyle{ \alpha_2\! }[/math]=[math]\displaystyle{ k_3 }[/math]/[math]\displaystyle{ \alpha_3\! }[/math] [math]\displaystyle{ \} }[/math],where Z refer to the set of integers.
A 3-D signal input sequence will be selectively enhanced by a 3-D passband enclosing this line. Thus we make use of a cone filter having a thin pyramidal shaped passband which is approximated using Mixed filter constructed using 2-D DHT.
10.2. Design of a 3-D MixeD Cone Filter Using 2-D DHT[1]
Firstly, we have to select the passband regions on {k1,k2}. The close examination of DFT and DHT, shows that the 3-D DHT of [math]\displaystyle{ X_H }[/math](k(3)) of a spatially-planar signal x(n(3)) is zero outside the straight line [math]\displaystyle{ L_H }[/math](k(3)) passing through the origin of 3-D DHT (k(3)) space. Therefore, (k(3)) [math]\displaystyle{ \in }[/math] [math]\displaystyle{ \{ }[/math] Z[math]\displaystyle{ \vert }[/math] [math]\displaystyle{ k_1 }[/math]/[math]\displaystyle{ \alpha_1\! }[/math]=[math]\displaystyle{ k_2 }[/math]/[math]\displaystyle{ \alpha_2\! }[/math]}, where Z refer to the set of integers. All the LDE's that correspond to 2-tuples {[math]\displaystyle{ k_1 }[/math],[math]\displaystyle{ k_2 }[/math]}, that lie outside the fan shaped projection of the thin pyramidal passband on the [math]\displaystyle{ k_1 }[/math]-[math]\displaystyle{ k_2 }[/math] plane have to be omitted. The half angle will determine the k1-k2 plane bandwidth of the MixeD filter.
Secondly, we have to find the characteristics of the LDE Input sequences [math]\displaystyle{ X_H }[/math]([math]\displaystyle{ k_1 }[/math],[math]\displaystyle{ k_2 }[/math],[math]\displaystyle{ n3 }[/math]). The LDE input sequences computed for the 2-D DHT of a S-P signal x(n(3)), are real and sinusoidal in the steady-state. Since a spatially planar signal is also a linear trajectory signal, it maybe written in the form, x(n(3)) = x([math]\displaystyle{ n_1 }[/math] - [math]\displaystyle{ p_1 }[/math][math]\displaystyle{ n_3 }[/math], [math]\displaystyle{ n_2 }[/math] - [math]\displaystyle{ p_2 }[/math][math]\displaystyle{ n_3 }[/math],[math]\displaystyle{ n_3 }[/math] ), where [math]\displaystyle{ p_1 }[/math] = [math]\displaystyle{ \alpha_3\! }[/math]/[math]\displaystyle{ \alpha_1\! }[/math] and [math]\displaystyle{ p_2 }[/math] = [math]\displaystyle{ \alpha_3\! }[/math]/[math]\displaystyle{ \alpha_2\! }[/math].
Now, using the shift property of 2-D DHT, we get, [math]\displaystyle{ X_H }[/math]([math]\displaystyle{ k_1 }[/math],[math]\displaystyle{ k_2 }[/math],[math]\displaystyle{ n_3 }[/math]) = [math]\displaystyle{ X_H }[/math]([math]\displaystyle{ k_1 }[/math],[math]\displaystyle{ k_2 }[/math],0)cos[math]\displaystyle{ \{ }[/math]W[math]\displaystyle{ \} }[/math] + [math]\displaystyle{ X_H }[/math](N - [math]\displaystyle{ k_1 }[/math], N - [math]\displaystyle{ k_2 }[/math],0)cos[math]\displaystyle{ \{ }[/math]W[math]\displaystyle{ \} }[/math], where W = cos[math]\displaystyle{ \{ }[/math]2([math]\displaystyle{ p_1 }[/math][math]\displaystyle{ k_1 }[/math] + [math]\displaystyle{ p_2 }[/math][math]\displaystyle{ k_2 }[/math])([math]\displaystyle{ n_3 }[/math][math]\displaystyle{ \pi }[/math])/N[math]\displaystyle{ \} }[/math]. This equation implies that the passband sequences, [math]\displaystyle{ X_H }[/math]([math]\displaystyle{ k_1 }[/math],[math]\displaystyle{ k_2 }[/math],[math]\displaystyle{ n3 }[/math]) at each tuple {[math]\displaystyle{ k_1 }[/math],[math]\displaystyle{ k_2 }[/math]} are real sampled sinusoids that may be selectively transmitted by employing LDE's that are characterized by narrowband bandpass magnitude frequency respone having Normalized frequencies given by,
v = 2([math]\displaystyle{ p_1 }[/math][math]\displaystyle{ k_1 }[/math] + [math]\displaystyle{ p_2 }[/math][math]\displaystyle{ k_2 }[/math])/N. If we choose the bandwidths B{[math]\displaystyle{ k_1 }[/math],[math]\displaystyle{ k_2 }[/math]} of these narrowband bandpass LDEs to be proportional to the centre frequencies v, so that B{[math]\displaystyle{ k_1 }[/math],[math]\displaystyle{ k_2 }[/math]} = Kv, K > 0, and K constant, the required 3D pyramidal passband is realized. Thus it has been proved that 2-D DHT helped in the constructing a MixeD 3-D filter.
The content is sourced from: https://handwiki.org/wiki/Multidimensional_filter_design_and_implementation
References
- K.S. Knudsen and T. Bruton, "Mixed Multidimensional Filters" IEEE transactions on "Circuits and Systems for Video Technology"
- Knud Steven Knudsen and Leonard T. Bruton "Mixed Domain Filtering of Multidimensional Signals", IEEE transactions on "Circuits and Systems for Video Technology", VOL. I , NO. 3, SEPTEMBER 1991
- Kwan, H. K., and C. L. Chan. "Multidimensional spherically symmetric recursive digital filter design satisfying prescribed magnitude and constant group delay responses." IEE Proceedings G (Electronic Circuits and Systems). Vol. 134. Issue 4, pp. 187 – 193, IET Digital Library, 1987
- Dan E. Dudgeon, Russell M. Mersereau, "Multidimensional Digital Signal Processing", Prentice-Hall Signal Processing Series, ISBN:0136049591, 1983.
- Russell M.Mersereau, Wolfgang F.G. Mecklenbrauker, and Thomas F. Quatieri, Jr., "McClellan Transformation for 2-D Digital Filtering: I-Design," IEEE Trans. Circuits and Systems, CAS-23, no. 7 (July 1976),405-14.
- Wolfgang F.G. Mecklenbrauker and Russell M. Mersereau, "McClellan Transformations for 2-D Digital Filtering: II-Implementation," IEEE Trans. Circuits and Systems, CAS-23, no.7(July 1976), 414-22.
- James H. McClellan and David S.K. Chan. "A 2-D FIR Filter Structure Derived from the Chebyshev Recursion," IEEE Trans. Circuits and Systems, CAS-24, no.7 (July 1977), 372-78.
- Roh T., Bogdan D.,Vandenberghe L., "Multidimensional FIR Filter Design Via Trigonometric Sum-of-Squares Optimization," 'IEEE JOURNAL OF SELECTED TOPICS IN SIGNAL PROCESSING (12/2007)', Vol. 1, No. 4, Page 1-10
- Ekstrom, Michael P., Richard E. Twogood, and John W. Woods. "Two-dimensional recursive filter design--A spectral factorization approach." Acoustics, Speech and Signal Processing, IEEE Transactions on 28.1 (1980): 16-26.
