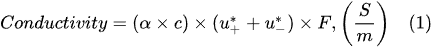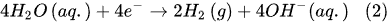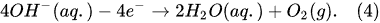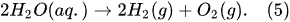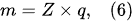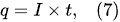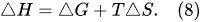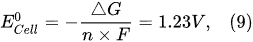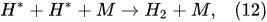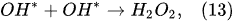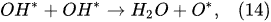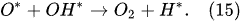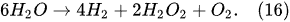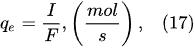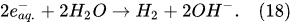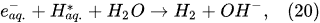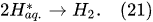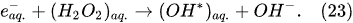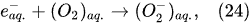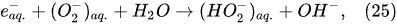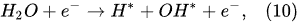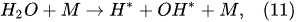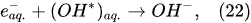Physicochemical Processes Leading to Plasma-Driven Solution Electrolysis: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Contributor:
Sergii Bespalko
,
Jerzy Mizeraczyk

A new type of electrolysis, initially known as the contact glow-discharge electrolysis (CGDE) and, more recently, as the plasma-driven solution electrolysis (PDSE), has attracted attention as an alternative method of hydrogen production. PDSE is a nontypical electrochemical process in which electric plasma is formed in the glow discharges excited by the direct or pulsed current in a gas–vapor envelope in the vicinity of the discharge electrode immersed in the electrolytic solution. The yield of chemicals in PDSE (i.e., the ratio of the moles of the product formed to the moles of electrons consumed in a chemical reaction) is several times higher than the Faradaic production of chemicals (predicted by Faraday’s law). In PDSE, new chemical compounds can also be synthesized, which does not happen using Faradaic electrolysis.

  • electrolytic solution
  • plasma electrolysis
  • contact glow-discharge electrolysis (CGDE)
  • plasma-driven solution electrolysis (PDSE)
  • hydrogen
  • hydrogen production

1. Introduction

The studies of the formation of PDSE in the electrolytic solution [1][2][3][4][5] showed that several processes must occur before the plasma is induced at the electrode surface. They are the Faradaic electrolysis, the Joule heating of the electrolytic solution, the solution evaporation at the electrode, the ionization of the gas–vapor mixture within the limited volume (called the envelope) around the discharge electrode, and eventually, the electrical discharges across the envelope.

2. Faradaic Electrolysis

It is well known that electrolysis is an electrochemical process that occurs when a direct or pulsed current passes through the electrolytic cell. To perform electrolysis, the electrolytic cell must contain the following essential components:
  • An electrolytic solution containing free ions, which can carry an electric current. In the Faradaic electrolysis of acidic and alkaline aqueous solutions, strong acids and alkalis, such as sulfuric acid (H2SO4), potassium (KOH), and sodium (NaOH) hydroxides, are used as electrolytes due to their strong ability to dissociate into positive ions (called cations) and negatively charged ions (called anions), which easily conduct electricity in the electrolytic solution [6][7][8].
  • A direct or pulsed current supply, which provides the necessary energy to create the direct motion of ions in the electrolytic solution.
  • Additionally, two electrodes, which are electrical conductors providing physical contact between the current supply and the electrolytic solution. In alkaline electrolysis, low-cost, non-precious, nickel-based alloys and stainless steel are used as the cathode and anode electrode materials, respectively [9][10].
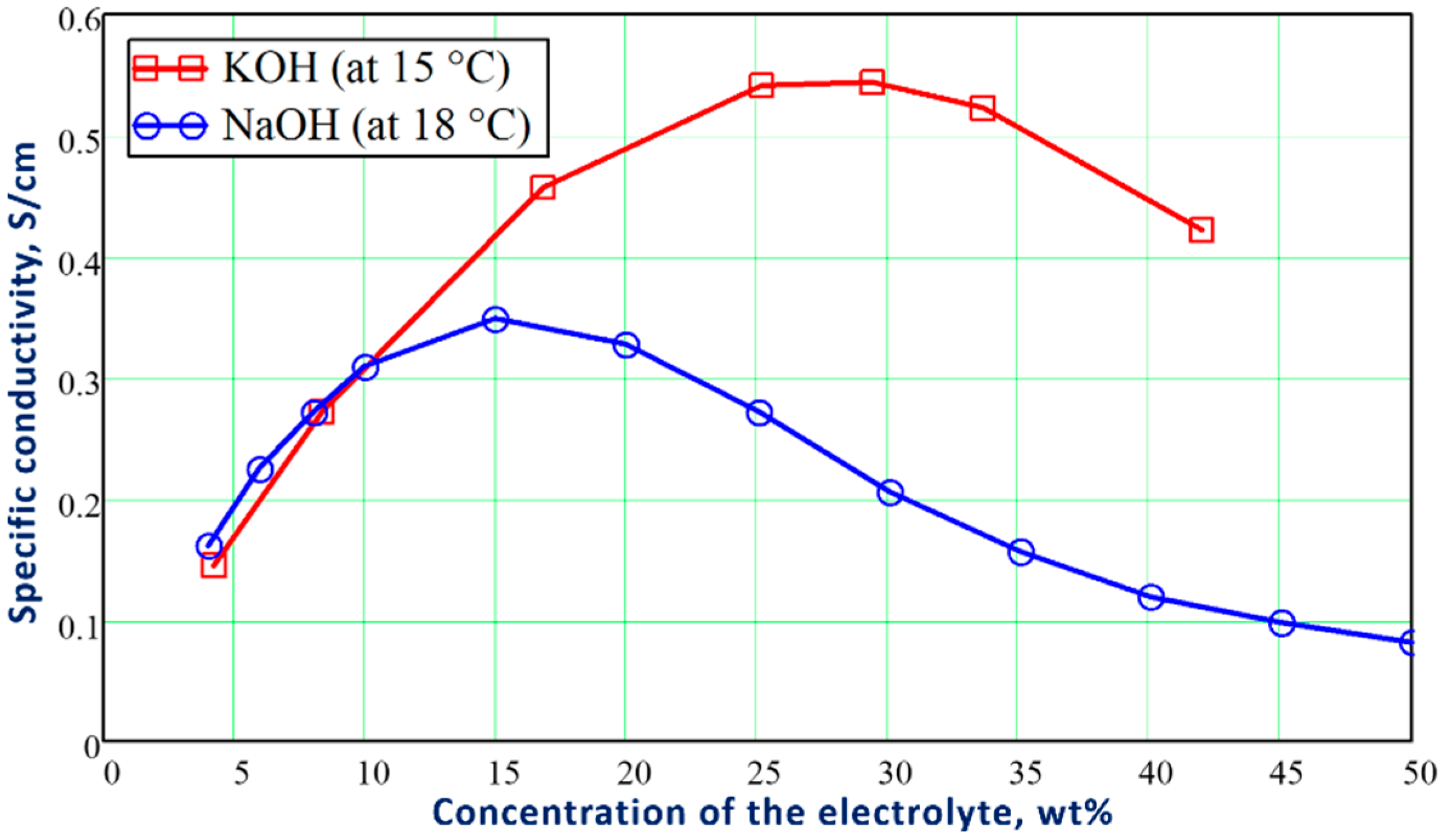
Figure 1 shows the influence of the weight concentration of KOH and NaOH electrolytes on the specific conductivity of their aqueous solutions.
Figure 1. Influence of the weight concentration of KOH and NaOH on the specific conductivity of their aqueous solutions at 15 °C and 18 °C, respectively. The diagram was built based on the tabular data presented in [11].
According to Kohlrausch’s law of independent ionic migration, both cations and anions contribute to the conductivity of the electrolytic solutions. Thus, the specific conductivity of the electrolytic solutions can be estimated using the following formula [12]:
where α is the dissociation degree of the diluted electrolyte, c is the molar concentration of the electrolyte (mol/m3), u∗+ and u∗− are the electrical mobilities of cations and anions, respectively (m2/V⋅s), F is the Faraday constant, F=96485 C/mol. Since potassium cations K+ have higher electrical mobility than sodium cations Na+ (u∗+=7.6×10−8 m2/(V⋅s) for K+ cations versus u∗+=5.2×10−8 m2/(V⋅s) for Na+ cations [12]), the KOH aqueous solution has higher specific conductivity at the same concentration compared to the NaOH aqueous solution, as can be seen in Figure 1.
To decrease the resistance losses in the electrolytic cell, the electrolyte concentration is selected in the optimal range to have the highest conductivity of the electrolytic solution. For this reason, the optimal range of the concentration for KOH electrolyzers varies between 25–30 wt% [13].
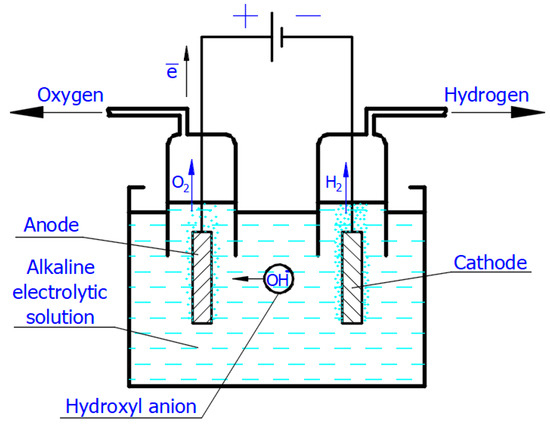
Applying the voltage from the direct current supply to the electrodes immersed in the electrolytic solution causes the motion of free ions (Figure 2). Thus, in the Faradaic electrolysis of aqueous solutions of hydroxides of active metals situated at the top of the reactivity series of metals (from Cesium Cs to Aluminum Al), at the negative electrode called the cathode, the reduction reaction of the water molecules with electrons taken from the cathode occurs only to form hydrogen molecules and negatively charged hydroxyl ions [10]:
Energies 15 07508 g002 550
Figure 2. Scheme of the simplest alkaline electrolytic cell illustrating production of H2 and O2 according to Equations (2) and (4). The scheme shows only hydroxyl anions participating in the charge transport.
As seen from Equation (2), the cations of active metals do not participate in this electrochemical reaction. However, as recently reported by Monteiro et al. [14], the metal cations in the electrolytic solution have a significant effect on the activity of the cathode reaction (also known as the hydrogen evolution reaction) occurring on different metallic surfaces.
In the electrolysis of aqueous solutions of hydroxides or salts of metals situated in the middle of the reactivity series of metals (from titanium Ti to lead Pb), in addition to the hydrogen-generating reaction (Equation (2)) at the cathode, the reduction reaction of n-fold positively charged metal ions takes place as well [12]:
The solvated hydroxyl ions formed at the cathode (Equation (2)) migrate through the electrolytic solution to the positive electrode called the anode, where they are oxidized into molecular oxygen and water [15]:
The overall reaction of water decomposition can be described by the following equation [10]:
Thus, in the Faradaic electrolysis of alkaline solutions with the electrodes having an equal surface area, the number of hydrogen moles produced at the cathode doubles the number of oxygen moles produced at the anode.
According to Faraday’s first law of electrolysis, the substance mass evolved at the electrode surface in the electrolysis is proportional to the quantity of electric charge passed through the electrolytic solution, i.e., [12]:
where m is the evolved substance mass, Z is the so-called electrochemical equivalent, and q is the electric charge passed through the electrolytic solution. The electrochemical equivalent Z of a chemical element is the mass of the element transported by an electric charge of one Coulomb. For example, the electrochemical equivalent for hydrogen is 1.044 × 10−8 kg/C [16]. The electric charge passing through the electrolytic solution is given by the formula [12]:
where I is the current flowing through the electrolytic solution, and t is the duration of the electrolysis.
In the standard conditions (p = 101 325 Pa, T = 298 K), the decomposition of each mole of water demands a theoretical minimum of electrical energy input of 237.23 kJ, which is known as the change of the standard Gibbs free energy of water (ΔG). It also demands some external heat input of 48.6 kJ, known as the bound energy (TΔS), which should be delivered to the electrolytic solution at temperature T to raise its entropy by ΔS. Therefore, the water decomposition cannot proceed without supplying the energy of 285.83 kJ per mole of water. This energy is known as the change of the standard enthalpy of water (ΔH). These thermodynamic functions, such as the change of the enthalpy, Gibbs free energy, and bound energy, are known as the thermodynamic potentials. They are interlinked with each other by the equation [17]:
In the standard conditions, the standard potential of the electrolytic cell can be calculated using the following formula [17]:
where ΔG is the change of the standard Gibbs free energy of water, n is the number of electrons per mole of products (n = 2), and F is the Faraday constant.
However, this value of the standard potential is theoretical, and practically, due to the ohmic losses and other side reactions, the electrolytic cell operates at a certain overpotential. In industrial electrolyzers, the actual potential of the electrolytic cells varies from 1.7 to 2.5 V. This overpotential decreases the energy yield of hydrogen production.
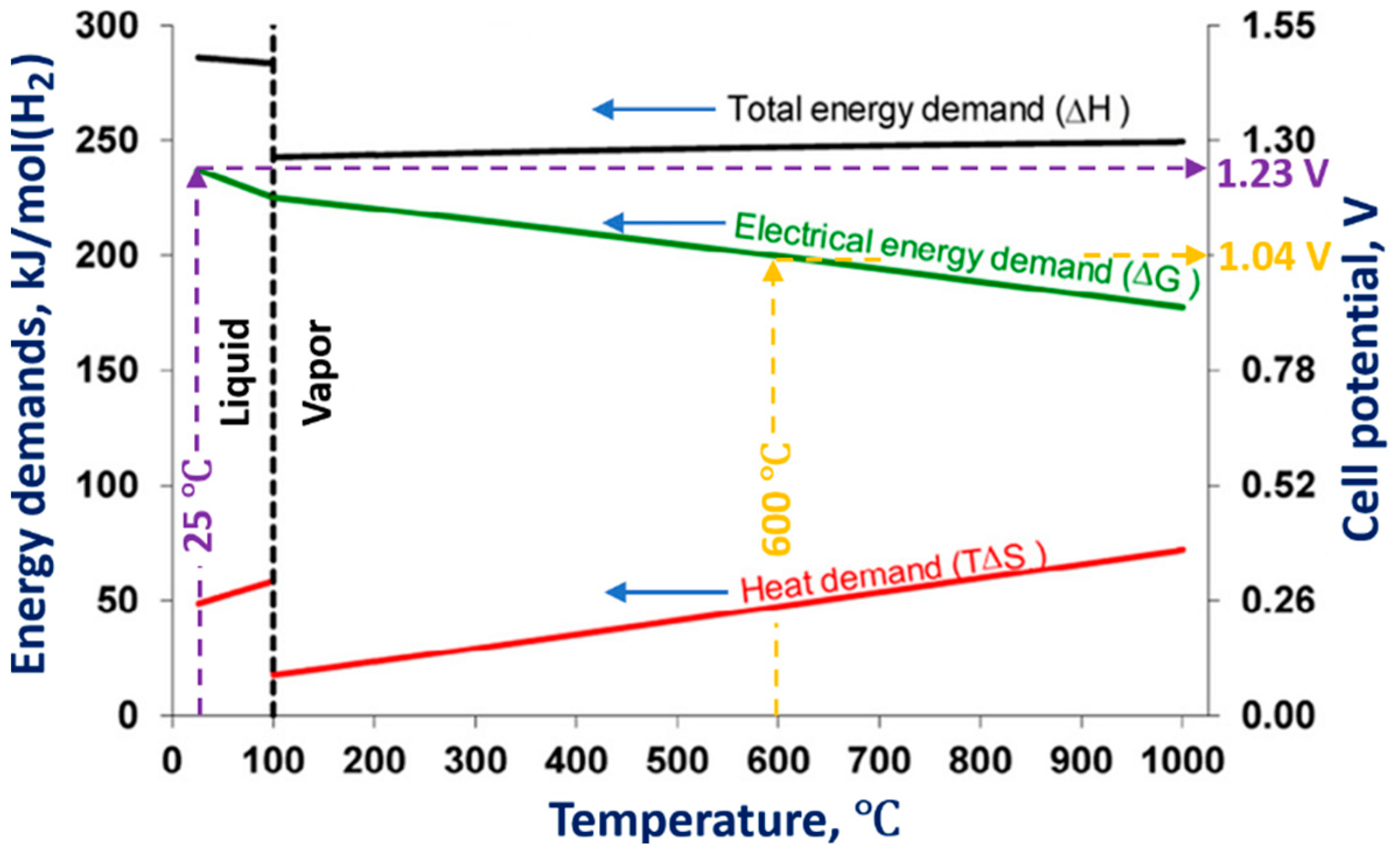
One way to improve the energy yield of hydrogen production is to decrease the electrolytic cell’s overpotential by increasing the electrolytic solution’s temperature. Figure 3 shows the influence of the electrolytic solution temperature on the changes of enthalpy (ΔH), Gibbs free energy (ΔG), and bound energy (TΔS).
Figure 3. Influence of the temperature of the electrolytic solution on the energy demands for water decomposition. Reprinted from [18] with permission from Elsevier. Changes in the cell potential for 25 °C and 600 °C of the electrolytic solution temperatures are also shown.
As can be seen from Figure 3, an increase in the temperature of the electrolytic solution leads to a decrease in the Gibbs free energy, which results in the decrease in the electrical energy input required to carry out the water decomposition. Performing the electrolysis at an elevated temperature to produce hydrogen is called high-temperature water/steam electrolysis.
At higher temperatures, more expensive electrical energy (attributed to the change of the Gibbs free energy ΔG) needed for the water decomposition can be substituted by less expensive thermal energy (the bound energy TΔS). The thermal energy can be delivered from some waste heat source, which makes the high-temperature water/steam electrolysis attractive from an economic point of view.
Figure 3 also shows values of the cell potentials needed to be applied for the water decomposition at 25 °C and 600 °C. At 25 °C, the cell potential is 1.23 V, whereas at 600 °C, which corresponds to the steam electrolysis, the cell potential is 1.04 V. These values are found as the projections of the intersection points of isotherms (vertical dashed lines in Figure 3) of 25 °C and 600 °C with the electrical energy demand line (ΔG) to the cell potential axis (right-hand vertical axis). Practically, in the high-temperature water/steam electrolysis, the potential of the electrolytic cell can be reduced below 1 V [18][19].

3. Transformation of the Faradaic Electrolysis into PDSE

The Faradaic electrolysis transforms into PDSE with an increased applied voltage that has a value sufficient to ionize the species in the gas–vapor envelope at the electrode, and subsequently, induce the electrical discharge plasma in the envelope.
Regardless of the electric potential polarity, the plasma is formed at the electrode, which its active surface area (immersed in the electrolytic solution) is smaller than that of the other electrode. The electrode at which the plasma is formed is called the discharge electrode [20]. If the smaller electrode is positively charged (being an anode), the discharge formed around it is called the anodic glow discharge. If the smaller electrode is negatively charged (being a cathode), the discharge around it is called the cathodic glow discharge (see Figure 4). Correspondingly, PDSE is either the anodic or cathodic regime of PDSE. The length of electrodes exposed to the electrolytic solution is called the active length of the electrodes.
In the anodic and cathodic regimes of PDSE, the plasma around the discharge electrode takes over the role of the positive and negative electrode, respectively, whereas the second electrode (larger one) immersed in the electrolytic solution with no plasma formation acts as a counter electrode. In PDSE, the plasma–liquid interaction allows both electrochemical and plasma-chemical synthesis of the substances [1][21].
Figure 4a–e illustrates the transformation of the electrolysis from its Faradaic form into PDSE.
Figure 4a shows a typical electrolytic cell with a smaller and a larger electrode for PDSE before applying DC voltage. Figure 4b,d illustrates the formation of PDSE at the anode with the applied voltage, whereas Figure 4c,e illustrates the formation of PDSE at the cathode.
Figure 4b–e confirms that, regardless of the voltage polarity, both glow discharges, the anodic and cathodic, form at the electrode of a smaller active surface area, i.e., at the tungsten rod whose surface area is about 12 times smaller than that of the stainless-steel plate. In the anodic regime of PDSE, the plasma forms a thin layer around the tungsten rod (Figure 4d). The plasma formed in the cathodic regime of PDSE (Figure 4e) occupies a much larger volume around the tungsten rod than that in the anodic regime of PDSE (Figure 4d). This shows that the cathodic regime of PDSE is more efficient for steam generation. The brightness of the cathodic glow discharges is stronger than that of the anodic glow discharges, although the applied voltage is lower in the cathodic regime of PDSE (120 V in the cathodic regime of PDSE versus 130 V in the anodic regime of PDSE).
Sharma et al. [22] confirmed that the cathodic regime of PDSE can be applied for continuous steam generation with a steam generation efficiency of 80%. Zheng et al. [23] showed that in the cathodic regime of PDSE, the plasma formed around the discharge electrode is highly negative. The above differences in the microscopic appearance of the anodic and cathodic regimes of PDSE are due to the difference in the mechanisms of the formation of the glow discharges at the anode and cathode.
Figure 4. Transformation of the electrolysis from the Faradaic form into the anodic and cathodic regimes of PDSE with increasing applied voltage: (a) the electrolytic cell before applying DC voltage, (b) Faradaic electrolysis at an applied voltage of 20 V (tungsten rod served as an anode), (c) Faradaic electrolysis at an applied voltage of 20 V (tungsten rod served as a cathode), (d) the anodic regime of PDSE at the applied voltage of 130 V (discharge onset voltage was 60 V), (e) the cathodic regime of PDSE at the applied voltage of 120 V (discharge onset voltage was 52 V). The electrolytic solution was 10 wt% Na2CO3 water solution at the initial temperature of 22 °C and atmospheric pressure. The electrodes: a stainless-steel plate with a thickness of 0.4 mm and 2 cm × 2cm active surface area exposed to the electrolytic solution and a tungsten rod with a diameter of 2 mm. The active length of the stainless-steel plate was 2 cm. The active length of the tungsten rod was 1 cm. The ratio of the active surface area of the smaller electrode and that of the larger electrode is about 1/12 [24].
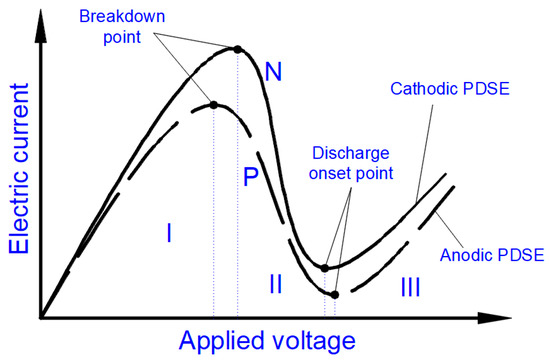
Figure 5 shows typical shapes of the current-voltage characteristics I(V) of the electrolysis comprising the Faradaic, transition, and PDSE phases. The current-voltage characteristics are shown for two cases: when the smaller electrode is positively (marked P) or negatively (marked N) charged. The case of a positively charged smaller electrode terminates with the anodic regime of PDSE, whereas the case of a negatively charged smaller electrode terminates with the cathodic regime of PDSE. Although the I(V) characteristics differ, they have similar shapes, and each has two extremum points, which divide the electrolysis into three phases (Figure 5). The first phase (marked I) is the Faradaic electrolysis. It ends at a breakdown point when the Faradaic electrolysis terminates due to the formation of a stable gas–vapor envelope around the discharge electrode due to the coalescence of gas and vapor bubbles. The gas and vapor bubbles are produced by the Faradaic electrolysis and by evaporation of the electrolytic solution, especially at higher electric current densities, causing higher Joule heating. The value of the electric current density at which the Faradaic electrolysis terminates (i.e., at the breakdown point) depends on the material of the discharge electrode, conductivity of the electrolytic solution, temperature, and surface tension [1].
Energies 15 07508 g005 550
Figure 5. A typical shape of the current-voltage characteristics of the electrolysis. The characteristics shown correspond to two cases: positively (P) and negatively (N) charged smaller electrode. The first case terminates with the anodic regime of PDSE. The second terminates with the cathodic regime of PDSE. Voltage regions: I—the Faradaic electrolysis (starting from 0 V and terminating at the breakdown point), II—the transition region (starting from the breakdown point and terminating at the discharge onset point), III—the anodic and cathodic regimes of PDSE (initiating at the discharge onset point). The experimental current-voltage characteristics can be found in [4][20][23][25][26][27][28][29].
When increasing the applied voltage above the value defined by the breakdown point, the second phase (marked II) appears. In this phase, the thickness of the gas–vapor envelope around the discharge electrode rises, leading to a decrease in the electric current (as seen in Figure 5) due to the rise in the electrical resistance through the gas and vapor in the envelope. According to the experimental study by Gupta and Singh [1], the electrical resistance of the gas–vapor envelope surrounding the discharge electrode is about 10 000 Ohms, whereas the electrical resistance of the electrolytic solution is a few orders of magnitude smaller. The applied voltage increasing in the second phase becomes high enough to cause the ionization of the gas–vapor envelope. The second phase ends when the ionization of the gas and vapor in the envelope transfers into the electrical discharge. This is marked on the I(V) characteristics by the second extreme point, called the discharge onset point.
At applied voltages higher than that pointed out by the discharge onset point, the electrolysis’s third phase (marked III) exists. This phase is called PDSE. The second phase is a transition between the first phase (the Faradaic electrolysis) and the third phase (PDSE). The second phase is called the transition phase.
Allagui and Elwakil [25] revealed that the transition phase of the current-voltage characteristic, recorded at positive and negative dV/dt (increasing- and decreasing-step voltage sweeps) of the cathodic regime of PDSE, contains hysteresis, which is explained by the transitional appearance/disappearance of the space charge structure, composed of the self-organized gas film on the one hand and the glow-discharge volume surrounding the working electrode on the other.
The second extreme point, named the discharge onset point, indicates the initiation of the electrical discharges within the gas–vapor envelope. That is why the third section of the current-voltage characteristic corresponds to the plasma formation in the electrolytic solution.
As shown in [30][31][32], the values of the breakdown and discharge onset voltages strongly depend on the conductivity of the electrolytic solution applied. In general, lower specific conductivities of the aqueous electrolytic solutions result in higher values of the breakdown and discharge onset voltages, e.g., the breakdown at the conductivity of the KCl aqueous solution of 5 mS/cm and discharge onset voltages are equal to 270 V and 310 V, respectively. At higher specific conductivities, both voltages significantly decrease. For example, for the conductivity of a KCl aqueous solution of 600 mS/cm, the breakdown and discharge onset voltages are 30 V and 90 V, respectively [32].
According to the results of the comprehensive investigations carried out by Sengupta et al. [1][2][3][4][5], the discharge onset voltage also depends on the polarity of PDSE. They found that in the anodic regime of PDSE, the discharge onset voltage was 420 V, whereas in the cathodic regime of PDSE, it was only 160 V in the same aqueous K2SO4 electrolytic solution with a 0.05 M concentration. That is why PDSE develops much easier in the cathodic regime than in the anodic regime under the same conditions. The same feature of the plasma formation in the cathodic and anodic regimes of PDSE was observed in another experiment, presented in Figure 4d,e. In the 10 wt% Na2CO3 aqueous solution, the discharge onset voltage was 52 V in the cathodic regime of PDSE, whereas it was 60 V in the anodic regime of PDSE.

4. Physicochemical Processes Occurring in the Cathodic and Anodic Regimes of PDSE

Previous studies [1][2][3][4][5][33] showed that in PDSE, the total yields (total amount of all substances produced at the discharge electrode) include chemical yields produced according to Faraday’s first law of electrolysis (Equation (6)), called the Faradaic yield (products), and extra amount of substances, the production of which does not obey Equation (6). This extra amount of substances is called the non-Faradaic yield (products). 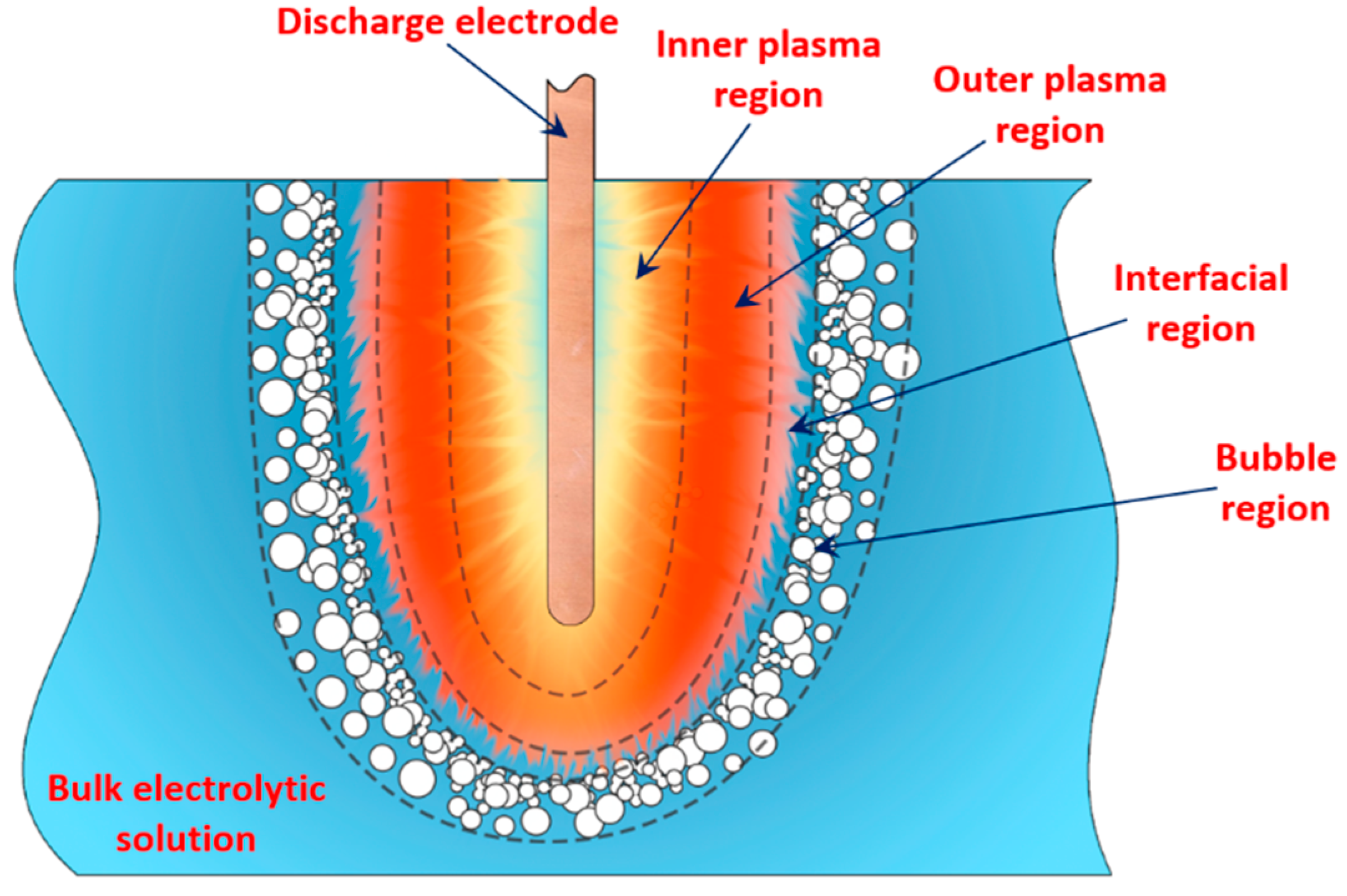The non-Faradaic yield of the anodic and cathodic regimes of PDSE is derived from two different reaction regions (Figure 6): i.e., the plasma region around the discharge electrode and the interfacial region (the aqueous electrolytic solution situated close to the plasma interface).
Figure 6. Illustration of the regions at the discharge electrode.
According to Gupta and Singh [1], at the discharge electrode in the cathodic regime of PDSE, the non-Faradaic yield (extra H2 yield over the Faradaic yield of H2, O2, and H2O2 yields) accounts for about 75% of the substances produced in the plasma region and about 25% of the substances produced in the interfacial region (Figure 6). In contrast to the cathodic regime of PDSE, at the discharge electrode in the anodic regime of PDSE, only about 20% of this extra amount of substances (extra O2 yield over the Faradaic yield of O2, H2, and H2O2 yields) are produced in the plasma region, and 80% is derived from the interfacial region.
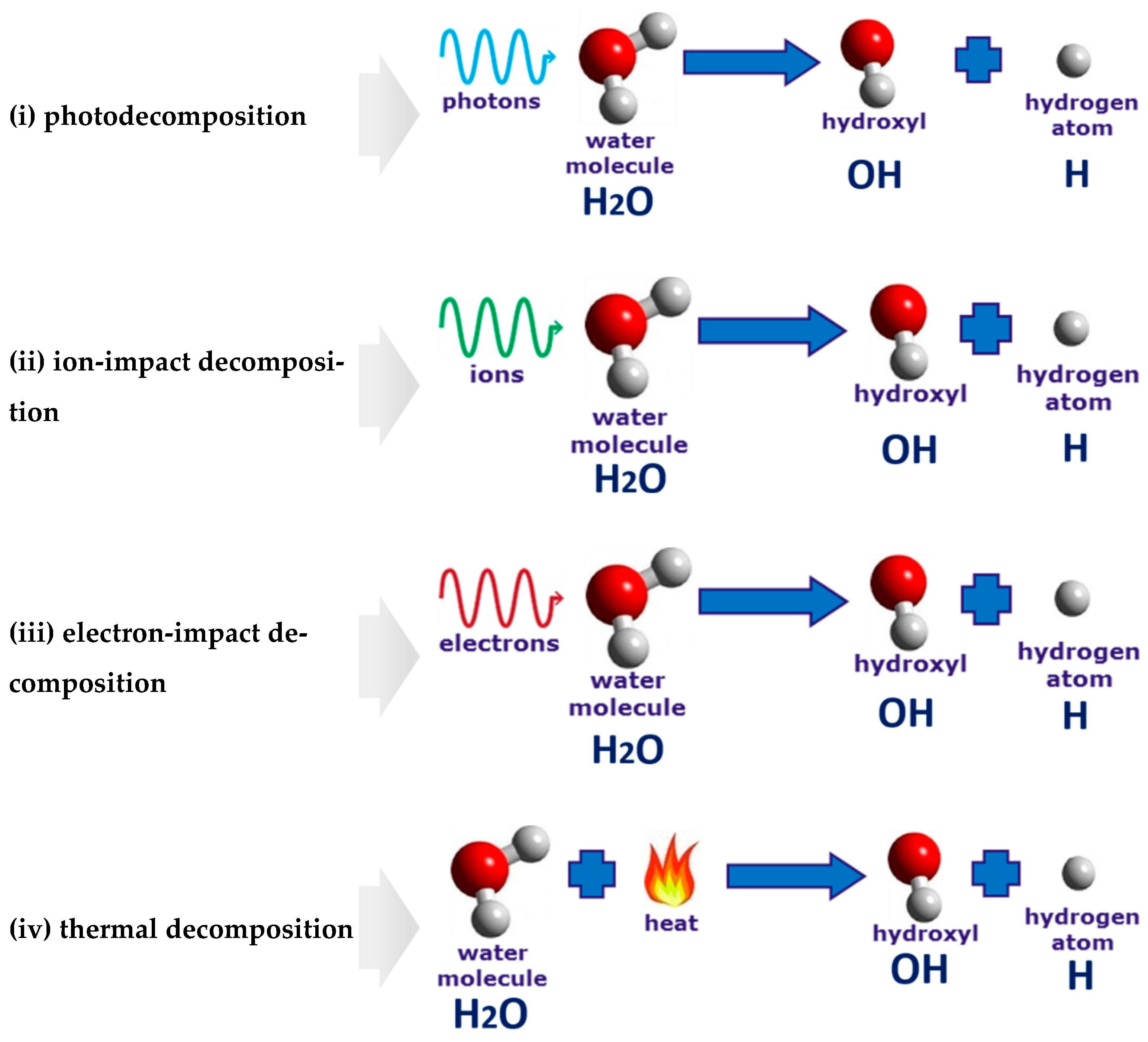
According to [34][35], four different processes are responsible for the decomposition of the water molecules in the vicinity of the discharge electrode. They are (i) photodecomposition, (ii) ion-impact decomposition, (iii) electron-impact decomposition, and (iv) thermal decomposition (Figure 7).
Figure 7. Illustration of the four processes leading to the water decomposition in the vicinity of the discharge electrode.
(i) Photodecomposition: The hydrogen production is the same as the water photolysis when the ultraviolet radiation emitted by the discharge plasma breaks up the hydrogen bonds in the water molecule [36][37].
(ii) Ion-impact decomposition: Ions contribute to the water-vapor decomposition. However, as was shown in [20], the ion-impact decomposition is less significant for hydrogen production than that of the electron-impact decomposition. However, when colliding with a metal surface of the electrode in the cathodic regime of PDSE, positively charged ions are responsible for promoting the emission of the secondary electrons.
(iii) Electron-impact decomposition: High-energy electrons dissociate water-vapor molecules into hydrogen and hydroxyl radicals. Studying the influence of the discharge polarity on hydrogen production, Zonhcheng Yan et al. [20] suggested that electrons are more essential species in initiating the water-vapor decomposition than ions.
(iv) Thermal decomposition: The process is similar to direct thermal water decomposition, which occurs at a high-temperature level, usually higher than 2500 K. For instance, at a temperature of 3000 K and a pressure of 1 bar, the degree of the water-vapor decomposition is around 65 vol% [38][39]. Paulmier et al. [35] suggested that the thermal dissociative process may play a significant role in PDSE. Thus, at a high temperature, the electrolytic solution near the electrode surface is strongly heated and vaporized; then, the water-vapor is thermally dissociated into hydrogen and oxygen.

4.1. Water-Vapor Decomposition in the Plasma Region

In the plasma around the discharge electrode, one of the mechanisms of the decomposition of water-vapor molecules into H2 and O2 molecules is a mechanism observed for the water-vapor decomposition in electrical discharges [40]. Mededovic and Locke [41] developed a model of plasma-in-liquid discharges. In this model, the plasma region consists of two subregions: inner and outer. Following up with the model developed by Mededovic and Locke [41], we may also assume the same subregions surrounding the discharge electrode in PDSE (Figure 6): an inner subregion, situated close to the discharge electrode with ionizing plasma, which dissociates water into OH* and H* radicals by the electron-impact and thermal processes, and an outer subregion, situated close to the plasma interface, in which radicals recombine, producing long-lived molecules such as H2, O2, and H2O2. The modeling results were confirmed experimentally in [41]. The set of the corresponding reactions occurring in those two subregions is presented below.
The water-vapor decomposition in the inner plasma subregion follows the reactions [41][42]:
where M is the water molecule [41] or a third collision body [42].
In the outer plasma subregion, recombination reactions take place, producing hydrogen peroxide H2O2, as well as hydrogen H2 and oxygen O2 [41]:
The overall stoichiometry of the molecular species formed by the pulsed electrical discharge in water follows the overall stoichiometry represented by the reaction given below [41]:

4.2. Plasma–Liquid Interaction in the Interfacial Region

Plasma–Liquid Interaction in the Cathodic Regime of PDSE

In the interfacial region (Figure 6), in the liquid-phase reaction zone near the plasma interface, one of the mechanisms responsible for the breakup of liquid H2O molecules into H2, H2O2, and O2 is the radiolysis-based reactions.
As shown by Mota-Lima et al. [43], in the cathodic regime of PDSE, the ballistic electrons are released from the plasma region into the liquid interfacial region at a rate which can be estimated by the following equation [43]:
where I is the electric current, and F is the Faraday constant.
After injection, the ballistic electrons become the hydrated electrons. The penetration depth into the interfacial region constitutes a few nanometers only [44]. Then, depending on the pH value of the electrolytic solution, the following mechanisms of the hydrogen-producing reactions were proposed [43]:
In the alkaline electrolytic solution, the water reduction via the self-recombination of the hydrated electrons occurs [43]:
In the electrolytic solution with an acidic nature, the hydrated electrons interact with the hydrogen ions, producing hydrogen radicals before the hydrogen production [43]:
Mota-Lima et al. [43] also proposed the following mechanisms of the side reactions, which reduce hydrogen production in the interfacial region. First, the interaction between the hydrated electrons and the plasma-synthesized species, such as the hydroxyl radicals and hydrogen peroxide, occurs [43]:
Second, the interaction between the hydrated electrons and the dissolved gases such as O2, N2, etc. in the interfacial region occurs, which takes over the scavenger role for the hydrated electrons [43]:
Both mechanisms of the side reactions occurring in the interfacial region lead to the formation of the hydroxyl ions, which, additionally, act as the hydrogen scavengers according to the recombination reaction described in Equations (13) and (14).

Plasma–Liquid Interaction in the Anodic Regime of PDSE

In the anodic regime of PDSE, one of the mechanisms of the plasma–liquid interaction follows Hickling’s radiolytic mechanism [26]. According to this mechanism, each H2O+gas ion, after acceleration in the steep anode, falls near the interfacial region and is driven into the aqueous electrolytic solution with energies sufficient to break-up liquid water molecules into H* and OH* radicals. Then, the formed radicals diffuse into the bulk of the electrolytic solution, where they undergo several reactions which are known to occur in pulse radiolysis.
The relative importance of the two mechanisms occurring in the plasma region (i.e., bombardment of the interfacial region by H2O+gas ions) and the interfacial region (i.e., diffusion of H2O+gas ions into the interfacial region with the subsequent break-up of the liquid water molecules) depends on the magnitude of the applied voltage. At the discharge onset voltage of 420 V, the occurring mechanism is the liquid-phase Hickling’s radiolytic mechanism, accounting for 90% of the non-Faradaic yield. However, with a further rise in voltage, the gas-phase mechanism, described in [5], becomes increasingly important and, at 500 V, accounts for 75% of the non-Faradaic yield.
For more details on the charge-transfer mechanisms in the anodic regime of PDSE, refer to the recent comprehensive study from Yerokhin et al. [45].
The Faradaic efficiency of hydrogen production in the plasma-driven solution electrolysis (PDSE), which exceeds 100%, is explained by different, in terms of their nature, reactions occurring in the vicinity of the discharge electrode. The first reaction type is based on the charge transfer. According to Faraday’s first law of electrolysis, hydrogen generation is directly proportional to the electric current passed through the electrolytic solution. In contrast to conventional electrolysis, a second mechanism consists of the gas-phase reactions in the plasma region. A solvent (water) and the organic additives, if any, are evaporated by the intense heating effect of the discharge plasma into the plasma region, where they serve as an additional source of hydrogen. The electron-impact decomposition of molecules in the plasma region is not based on the charge transfer and is non-Faradaic.
The two reaction mechanisms, one in the liquid interfacial region and another in the plasma region, produce hydrogen simultaneously. Therefore, the electron-impact decomposition occurring in the plasma region contributes to the Faradaic efficiency of more than 100%.
Moreover, three additional processes are also responsible for decomposing the water molecules and molecules of organic additives, if any, in the interfacial and plasma regions. They are photodecomposition, ion-impact decomposition, and thermal decomposition. These reaction pathways are not based on the charge transfer and they are non-Faradaic as well.
The actual reactions occurring within the plasma and interfacial regions in the anodic and cathodic regimes of PDSE are much more sophisticated than those shown above. Potential mechanisms of these interactions will be discussed in a future research paper dedicated to the fundamentals of PDSE.

This entry is adapted from the peer-reviewed paper 10.3390/en15207508

References

  1. Susanta K Sen Gupta; Rajshree Singh; Cathodic contact glow discharge electrolysis: its origin and non-faradaic chemical effects. Plasma Sources Science and Technology 2016, 26, 015005, 10.1088/0963-0252/26/1/015005.
  2. Susanta K. Sengupta; Om Prakash Singh; Contact glow discharge electrolysis: a study of its chemical yields in aqueous inert-type electrolytes. Journal of Electroanalytical Chemistry 1994, 369, 113-120, 10.1016/0022-0728(94)87089-6.
  3. Susanta K. Sengupta; Ashok K. Srivastava; Rajeshwar Singh; Contact glow discharge electrolysis: a study on its origin in the light of the theory of hydrodynamic instabilities in local solvent vaporisation by Joule heating during electrolysis. Journal of Electroanalytical Chemistry 1997, 427, 23-27, 10.1016/s0022-0728(96)05044-9.
  4. Susanta K. Sengupta; Rajeshwar Singh; Ashok K. Srivastava; A Study on the Origin of Nonfaradaic Behavior of Anodic Contact Glow Discharge Electrolysis: The Relationship Between Power Dissipated in Glow Discharges and Nonfaradaic Yields. Journal of The Electrochemical Society 1998, 145, 2209-2213, 10.1149/1.1838621.
  5. Urvashi Gangal; Monika Srivastava; Susanta K. Sen Gupta; Mechanism of the Breakdown of Normal Electrolysis and the Transition to Contact Glow Discharge Electrolysis. Journal of The Electrochemical Society 2009, 156, F131, 10.1149/1.3186023.
  6. Maximilian Schalenbach; Geert Tjarks; Marcelo Carmo; Wiebke Lueke; Martin Mueller; Detlef Stolten; Acidic or Alkaline? Towards a New Perspective on the Efficiency of Water Electrolysis. Journal of The Electrochemical Society 2016, 163, F3197-F3208, 10.1149/2.0271611jes.
  7. Marcelo Carmo; David L. Fritz; Jürgen Mergel; Detlef Stolten; A comprehensive review on PEM water electrolysis. International Journal of Hydrogen Energy 2013, 38, 4901-4934, 10.1016/j.ijhydene.2013.01.151.
  8. Qing Lei; Baoguo Wang; Peican Wang; Shuai Liu; Hydrogen generation with acid/alkaline amphoteric water electrolysis. Journal of Energy Chemistry 2019, 38, 162-169, 10.1016/j.jechem.2018.12.022.
  9. Alejandro N. Colli; Hubert H. Girault; Alberto Battistel; Non-Precious Electrodes for Practical Alkaline Water Electrolysis. Materials 2019, 12, 1336, 10.3390/ma12081336.
  10. Keith Scott. Chapter 1 Introduction to Electrolysis, Electrolysers and Hydrogen Production. In Electrochemical Methods for Hydrogen Production; Keith Scott, Eds.; Royal Society of Chemistry: London, UK, 2019; pp. 1-27.
  11. Zinchenko A.V., Izotova S.G., Rumyantsev A.V., Simanova S.A., Skripkin M.U., Slobodov A.A.. New Handbook of Chemist and Process Engineer. Chemical Equilibrium. Properties of Solutions (in Russian); Simanova S.A., Eds.; Professional: Saint Petersburg, Russia, 2004; pp. 998.
  12. Atkins, P.; de Paula, J.. Atkin’s Physical Chemistry; Jonathan Crowe, Jessica Fiorillo, Ruth Hughes, Eds.; W.H. Freeman and Company: New York, NY, USA, 2006; pp. 1085.
  13. Coutanceau, C.; Baranton, S.; Audichon, T.. Chapter 3-Hydrogen Production From Water Electrolysis. Hydrogen Electrochemical Production.; Christophe Coutanceau, Stève Baranton, Thomas Audichon, Eds.; Academic Press: Cambridge, MA, USA, 2017; pp. 17-62.
  14. Mariana C. O. Monteiro; Akansha Goyal; Pricilla Moerland; Marc T. M. Koper; Understanding Cation Trends for Hydrogen Evolution on Platinum and Gold Electrodes in Alkaline Media. ACS Catalysis 2021, 11, 14328-14335, 10.1021/acscatal.1c04268.
  15. Ali Keçebaş, Muhammet Kayfeci, Mutlucan Bayat. Chapter 9-Electrochemical hydrogen generation. In Solar Hydrogen Production; Francesco Calise, Massimo Dentice D’Accadia, Massimo Santarelli, Andrea Lanzini, Domenico Ferrero, Eds.; Academic Press: Cambridge, MA, USA, 2019; pp. 299–317.
  16. Elektrochemisches Äquivalent . Wikipedia. Retrieved 2022-10-28
  17. Sanford Klein, Gregory Nellis. Thermodynamics; Cambridge University Press: Cambridge, MA, USA, 2012; pp. 1102.
  18. Alexander Buttler; Hartmut Spliethoff; Current status of water electrolysis for energy storage, grid balancing and sector coupling via power-to-gas and power-to-liquids: A review. Renewable and Sustainable Energy Reviews 2018, 82, 2440-2454, 10.1016/j.rser.2017.09.003.
  19. Sukhvinder P.S. Badwal; Sarbjit Giddey; Christopher Munnings; Hydrogen production via solid electrolytic routes. WIREs Energy and Environment 2012, 2, 473-487, 10.1002/wene.50.
  20. ZongCheng Yan; Li Chen; Honglin Wang; Hydrogen generation by glow discharge plasma electrolysis of ethanol solutions. Journal of Physics D: Applied Physics 2008, 41, 155205, 10.1088/0022-3727/41/15/155205.
  21. Peter J. Bruggeman; Renee R. Frontiera; Uwe R. Kortshagen; Mark J. Kushner; Suljo Linic; George C. Schatz; Himashi Andaraarachchi; Stephen Exarhos; Leighton O. Jones; Chelsea M. Mueller; et al. Plasma-driven solution electrolysis. Journal of Applied Physics 2021, 129, 200902, 10.1063/5.0044261.
  22. Neeraj Sharma; Gerardo Diaz; Edbertho Leal-Quirós; Evaluation of contact glow-discharge electrolysis as a viable method for steam generation. Electrochimica Acta 2013, 108, 330-336, 10.1016/j.electacta.2013.06.108.
  23. Bocong Zheng; Keliang Wang; Maheshwar Shrestha; Thomas Schuelke; Qi Hua Fan; Understanding the chemical reactions in cathodic plasma electrolysis. Plasma Sources Science and Technology 2019, 28, 085016, 10.1088/1361-6595/ab36a6.
  24. Sergii Bespalko; The plasma discharges in the anodic and cathodic regimes of plasma driven solution electrolysis for hydrogen production. PRZEGLĄD ELEKTROTECHNICZNY 2022, 1, 124-127, 10.15199/48.2022.09.26.
  25. Anis Allagui; Ahmed S. Elwakil; On the N-shaped Conductance and Hysteresis Behavior of Contact Glow Discharge Electrolysis. Electrochimica Acta 2015, 168, 173-177, 10.1016/j.electacta.2015.03.154.
  26. A. Hickling; M. D. Ingram; Contact glow-discharge electrolysis. Trans. Faraday Soc. 1964, 60, 783-793, 10.1039/tf9646000783.
  27. Zong Cheng Yan; Chen Li; Wang Hong Lin; Hydrogen generation by glow discharge plasma electrolysis of methanol solutions. International Journal of Hydrogen Energy 2009, 34, 48-55, 10.1016/j.ijhydene.2008.09.099.
  28. Gao Jinzhang; Wang Aixiang; Fu Yan; Wu Jianlin; Ma Dongping; Guo Xiao; Li Yan; Yang Wu; Analysis of Energetic Species Caused by Contact Glow Discharge Electrolysis in Aqueous Solution. Plasma Science and Technology 2008, 10, 30-38, 10.1088/1009-0630/10/1/07.
  29. Genki Saito; Yuki Nakasugi; Tomohiro Akiyama; Generation of solution plasma over a large electrode surface area. Journal of Applied Physics 2015, 118, 023303, 10.1063/1.4926493.
  30. Xing-Long Jin; Xiao-Yan Wang; Hong-Mei Zhang; Qing Xia; Dong-Bin Wei; Jun-Jie Yue; Influence of Solution Conductivity on Contact Glow Discharge Electrolysis. Plasma Chemistry and Plasma Processing 2010, 30, 429-436, 10.1007/s11090-010-9220-0.
  31. Xinglong Jin; Xiaoyan Wang; Junjie Yue; Yaqi Cai; Hongyu Zhang; The effect of electrolyte constituents on contact glow discharge electrolysis. Electrochimica Acta 2010, 56, 925-928, 10.1016/j.electacta.2010.09.079.
  32. Giovanni Battista Alteri; Matteo Bonomo; Franco Decker; Danilo Dini; Contact Glow Discharge Electrolysis: Effect of Electrolyte Conductivity on Discharge Voltage. Catalysts 2020, 10, 1104, 10.3390/catal10101104.
  33. Gao Jin-Zhang; Wang Xiao-Yan; Hu Zhong-Ai; Hou Jing-Guo; Lu Quan-Fang; A Review on Chemical Effects in Aqueous Solution induced by Plasma with Glow Discharge. Plasma Science and Technology 2001, 3, 765-774, 10.1088/1009-0630/3/3/003.
  34. Jen-Shih Chang, Arnold J. Kelly, Joseph M. Crowley. Handbook of Electrostatic Processes; Marcel Dekker Inc.: New York, NY, USA, 1995; pp. 763.
  35. T. Paulmier; J.M. Bell; P.M. Fredericks; Development of a novel cathodic plasma/electrolytic deposition technique: Part 2: Physico-chemical analysis of the plasma discharge. Surface and Coatings Technology 2007, 201, 8771-8781, 10.1016/j.surfcoat.2006.07.066.
  36. Gamburg, D.Y.; Semenov, V.P.; Dubovkin, N.F.. Hydrogen: Properties, Production, Storage, Transportation, and Applications (in Russian); Khimiya: Moscow, Russia, 1989; pp. 672.
  37. Akihiko Kudo; Yugo Miseki; Heterogeneous photocatalyst materials for water splitting. Chemical Society Reviews 2008, 38, 253-278, 10.1039/b800489g.
  38. Vargaftic, N.B.. Handbook on Thermal Properties of Gases and Liquids (in Russian); Nauka: Moscow, Russia, 1972; pp. 720.
  39. Canan Acar, Ibrahim Dincer. 3.1 Hydrogen Production. In Comprehensive Energy Systems.; Ibrahim Dincer, Eds.; Elsevier: Netherlands, 2018; pp. 1-40.
  40. von Engel, A.. Ionized Gases; Clarendon Press: Oxford, UK, 1965; pp. 324.
  41. S Mededovic; Bruce Locke; Primary chemical reactions in pulsed electrical discharge channels in water. Journal of Physics D: Applied Physics 2007, 40, 7734-7746, 10.1088/0022-3727/40/24/021.
  42. Bruce R. Locke; Selma Mededovic Thagard; Analysis and Review of Chemical Reactions and Transport Processes in Pulsed Electrical Discharge Plasma Formed Directly in Liquid Water. Plasma Chemistry and Plasma Processing 2012, 32, 875-917, 10.1007/s11090-012-9403-y.
  43. Andressa Mota-Lima; Jailton Ferreira Do Nascimento; Osvaldo Chiavone-Filho; Claudio Augusto Oller Nascimento; Electrosynthesis via Plasma Electrochemistry: Generalist Dynamical Model To Explain Hydrogen Production Induced by a Discharge over Water. The Journal of Physical Chemistry C 2019, 123, 21896-21912, 10.1021/acs.jpcc.9b04777.
  44. Paul Rumbach; David M. Bartels; R. Mohan Sankaran; David B. Go; The solvation of electrons by an atmospheric-pressure plasma. Nature Communications 2015, 6, 7248, 10.1038/ncomms8248.
  45. Aleksey Yerokhin; Veta R. Mukaeva; Evgeny V. Parfenov; Nicolas Laugel; Allan Matthews; Charge transfer mechanisms underlying Contact Glow Discharge Electrolysis. Electrochimica Acta 2019, 312, 441-456, 10.1016/j.electacta.2019.04.152.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
ScholarVision Creations
Feedback