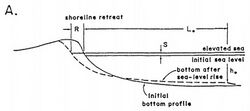
The Bruun Rule is a formula for estimating the magnitude of the retreat of the shoreline of a sandy shore in response to changes in sea level. Originally published in 1962 by Per Bruun, the Bruun Rule was the first to give a relationship between sea level rise and shoreline recession. The rule is a simple, two dimensional mass conversion, and remains in common use to estimate shoreline recession in response to sea level rise, despite criticism and modification, and the availability more complex alternate models.
- shoreline recession
- sea level rise
- sea level
1. The Rule
The Bruun Rule gives a linear relationship between sea level rise and shoreline recession based on equilibrium profile theory, which asserts that shore face profile maintains an equilibrium shape, and as sea level rises the increasing accommodation space forces this equilibrium profile landward and upward to preserve its shape relative to the new sea level.[1] As such, the Bruun Rule analysis assumes that the upper beach is eroded as the shore profile moves landward, and that the volume of eroded material is deposited offshore, resulting in a rise of the nearshore bottom which maintains a constant water depth.[2] The Bruun Rule predicts coastal recession to be as much as 10 to 50 times sea level rise, depending on the slope of the beach.[3]
The mathematical notation of the Bruun Rule is:
[math]\displaystyle{ R = \frac{SL}{h+B} = \frac{S}{\tan\beta} }[/math][4][5]
Where,
- R is shoreline recession, in metres
- S is sea level rise, in metres
- L is the horizontal length of the bottom affected by the sea level rise (from the dune peak to depth of closure), in metres
- h is the depth of closure (the water depth beyond which significant sediment transport does not occur[6][7]), in metres
- B is the dune height above sea level, in metres
- β is the average slope of the active profile[4]
2. History
In 1954, Per Moller Bruun published a paper[8] describing beach profiles and cross shore equilibrium.[9] Developing on these ideas, in 1962 he published his paper "Sea-Level Rise as a Cause of Shore Erosion",[10] which first gave a relationship between sea level rise and the shoreline recession of equilibrium beach profiles.[11] His rule wasn't given a name until 1967, when Schwartz published "The Bruun Theory of Sea-Level Rise as a Cause of Shore Erosion" which detailed laboratory and field tests of the theory and concluded that "the concept henceforth be known as "Bruun's Rule.""[12]
Per Bruun has since published works to clarify the limitations and practicality of his model, including "Review of Conditions for Uses of the Bruun Rule of Erosion" in 1983,[13] and "The Bruun Rule of Erosion by Sea-Level Rise: A Discussion on Large-Scale Two- and Three- Dimensional Usages" in 1988.[14] These publications outline the rule's limitations and practicality and stress that, though this model is intentionally two dimensional, it is applied to three dimensional environments in practice.[13][14] Bruun states that the rule "must be subjected to realistic adjustments"[13] for practical use.
As Bruun acknowledges, the Bruun Rule is a characteristically simple rule and has therefore been modified many times over, to account for more factors and in order to be accurately applicable in more cases.[15] The Bruun Rule has been most often modified to account for longshore transport, overwash, and Aeolian sediment transport.[15] For example, Dean and Maurmeier in 1983 modified the rule to be applicable to barrier shores and islands, some of which experience accretion instead of erosion.[1][16] Rosati et al. in 2013[15] and Dean and Houston in 2016[17] have modified the rule to account for onshore transport, and cross shore movement over the supposed depth of closure.[15][17] Further, Ashton et al. in 2011 modified the Bruun Rule for use on cliffed coasts,[18] and Hinkel et al. in 2013 used the rule as part of a wider methodology to describe the effects on sea level rise on and around tidal inlets.[19] The biggest challenge that remains seems to be isolating the effect of sea level rise on beach morphology from the coupled effects of wave energy, tidal currents, wind action, sediment supplies, sediment types and grain size, among others.[9][20]
In various forms and coupled with other models, the Bruun Rule has now been used to estimate shoreline responses to sea level rise worldwide.[3] The Bruun Rule has been applied to coasts including of the Caspian Sea,[21] Korean Peninsula,[22] Shuidong Bay,[23] Norfolk,[24] Rhode Island,[25] Florida,[26] Accra,[27] and Hawaii.[4]
3. Criticisms
The effect of climate change on beaches is challenging to accurately model, as it is an interdisciplinary subject that involves ocean, earth, and atmospheric science as well as civil engineering and policy.[28] Reliable coastal climate change impact assessments are needed to underpin effective strategies of adaptation in order to prepare growing coastal communities and high value coastal assets.[29] As a result, models for estimating coastal erosion as a result of sea level rise - including the Bruun Rule and models based on the Bruun Rule - are constantly being reviewed and updated.[4][6][7] The Bruun Rule has become the centre of much academic debate.[19]
In response to its inherent assumptions, the Bruun Rule has been widely criticised.[1][4][7][29][30][31][9] Some of the rule's most criticised assumptions include the nonexistence of gradients in longshore sediment transport, the existence of a depth of closure, a closed sediment budget, and the availability of sufficient sand sources.[1] In 2015, Andersen et al. labelled the Bruun Rule as " on its own...virtually unusable in open-ocean coastal environments"[4] due to its assumptions of physical environmental setting.[4]
One prominently criticised assumption of the Bruun Rule is its postulation of the net effects of longshore transport as negligible,[1][4][9] as the rule is by definition a two dimensional cross shore model that does not account for the longshore third dimension.[5] These longshore effects can, however, be the major cause of sediment erosion or deposition along beaches, dominating shoreline morphology and even masking the impacts of sea level rise as described by the Bruun Model.[1][4]
Another criticised assumption is the existence of a 'depth of closure'. The depth of closure is considered to be the water depth beyond which there are no significant changes in bed level, and is usually taken as the boundary between the upper shoreface, characterised by breaking waves and bars, and the lower shoreface, characterised by nonbreaking waves and a lack of bars.[1] The Bruun Rule stipulates that there is no significant sediment transfer across this boundary, however the strength of this concept in practice is debated.[1][9] The alternative R-DA model, proposed by Davidson-Arnott,[20] is based on the same assumptions as the Bruun Rule, except it recognises significant sediment transfer between the upper and lower shoreface, hypothesising that sediment is eroded from the lower shoreface and transported to the upper shoreface to maintain an equilibrium profile, and that as a result there is an upward and landward migration of the depth of closure with sea level rise.[1][20]
Cooper and Pilkey have been direct in their criticism of the Bruun Rule, publishing a paper in 2004 titled "Sea-level rise and shoreline retreat: time to abandon the Bruun Rule",[9] which is regularly cited in ensuing literature.[9] They argue that despite widespread criticism, the original Bruun Rule continues to be applied in inappropriate contexts, as outlined by Bruun[14] and experimental history, and that the Bruun Rule and its accompanying controversial assumptions are embedded in later models claiming to offer more sophisticated insights into coastal behaviour.[32] Cooper and Pilkey describe the use of the Bruun Rule as "a "one model fits all" approach"[9] to a range of complex coastal environments for which it is unfit to describe.[9] They list three main reasons that the rule "does not work":[9] its restrictive assumptions, the omission of important variables, and its reliance on outdated and erroneous concepts.[9] They describe the rule's restrictive assumptions as a closed materials balance, which ignores net longshore transport, and the lack of an accretionary component, that assumes sea level rise always results in beach recession, which together limit the rule's use to a small number of coasts.[9] Cooper and Pilkey list the omitted variables as the presence of outcrops or bottom currents, the effect of continental shelf slope on retreat rate, site specific feedback relationships, and the highly variable patterns of coastal evolution at millennial time scales, and the outdated and erroneous concepts relied upon as a universal equilibrium profile theory, a closure depth, and that unsupported idea that shoreface steepness has an effect on the rate of shore retreat.[9] They "conclude that [the Bruun Rule] has outlived its usefulness and should be abandoned",[9] however they have been criticised for providing no "meaningful alternative"[15] to the rule.
In his papers,[10][13][14] Bruun did not present a rigorous mathematical derivation for his rule, which has caused confusion in the research community.[16] For example, Rosen in 1978, Allison and Schwartz in 1981, Dean and Maurmeyer in 1983, and Zhang, Douglas and Leatherman in 2004 have all mathematically derived the Bruun Rule differently, with disagreement on the assumptions and limitations of the Bruun Rule unique to their own derivations.[16] However, the latter revision by Zhang et al.[16] presents an alternative derivation showing that "even though very simple, the Bruun model has considerable generality".[16]
Some field and laboratory tests have supported the Bruun Rule, although claimed experimental flaws in these publications have been criticised.[4] Amongst others, Ranasinghe and Stive in 2009,[5] and later Andersen et al. in 2015,[4] have concluded that "no study has produced comprehensive, well-accepted verification of the Brunn model".[4] However, there is a near consensus that the basic qualitative model of shoreline recession is valid,[2][4][5] despite quantitative data gleaned from the Bruun Rule being dubbed as "very coarse approximations"[4] or "broadly indicative estimates".[5] Despite these criticisms, the Bruun Rule is credited for its simplicity, and there remains "no simple, viable alternative".[15]
The content is sourced from: https://handwiki.org/wiki/Earth:The_Bruun_Rule
References
- Aagaard, Troels; Sørensen, Per (2012-01-02). "Coastal profile response to sea level rise: a process-based approach" (in en). Earth Surface Processes and Landforms 37 (3): 354–362. doi:10.1002/esp.2271. ISSN 0197-9337. https://dx.doi.org/10.1002%2Fesp.2271
- Scientific Committee on Ocean Research (SCOR) Working Group 89 (Summer 1991). "The Response of Beaches to Sea-Level Changes: A Review of Predictive Models". Journal of Coastal Research 7: 895–921.
- Le Cozannet, Gonéri; Garcin, Manuel; Yates, Marissa; Idier, Déborah; Meyssignac, Benoit (November 2014). "Approaches to evaluate the recent impacts of sea-level rise on shoreline changes". Earth-Science Reviews 138: 47–60. doi:10.1016/j.earscirev.2014.08.005. ISSN 0012-8252. https://dx.doi.org/10.1016%2Fj.earscirev.2014.08.005
- Anderson, Tiffany R.; Fletcher, Charles H.; Barbee, Matthew M.; Frazer, L. Neil; Romine, Bradley M. (2015-03-18). "Doubling of coastal erosion under rising sea level by mid-century in Hawaii" (in en). Natural Hazards 78 (1): 75–103. doi:10.1007/s11069-015-1698-6. ISSN 0921-030X. https://dx.doi.org/10.1007%2Fs11069-015-1698-6
- Ranasinghe, Roshanka; Stive, Marcel J. F. (2009-05-16). "Rising seas and retreating coastlines" (in en). Climatic Change 97 (3–4): 465–468. doi:10.1007/s10584-009-9593-3. ISSN 0165-0009. https://repository.tudelft.nl/islandora/object/uuid%3A2a14576d-03de-4775-9ecc-9e4be0dbe7c8/datastream/OBJ/download.
- Baron, Heather M.; Ruggiero, Peter; Wood, Nathan J.; Harris, Erica L.; Allan, Jonathan; Komar, Paul D.; Corcoran, Patrick (2014-09-13). "Incorporating climate change and morphological uncertainty into coastal change hazard assessments" (in en). Natural Hazards 75 (3): 2081–2102. doi:10.1007/s11069-014-1417-8. ISSN 0921-030X. https://dx.doi.org/10.1007%2Fs11069-014-1417-8
- Rollason, R.; Patterson, D.; Huxley, C. (2010). Assessing Shoreline Response to Sea Level Rise: An Alternative to the Bruun Rule. NSW Coastal Conference. http://www.coastalconference.com/2010/papers2010/Verity%20Rollason%20full%20paper.pdf.
- Bruun, Per (1954). "Coast erosion and the development of beach profiles.". Technical Memorandum 44: 82.
- Cooper, J. Andrew G.; Pilkey, Orrin H. (November 2004). "Sea-level rise and shoreline retreat: time to abandon the Bruun Rule". Global and Planetary Change 43 (3–4): 157–171. doi:10.1016/j.gloplacha.2004.07.001. ISSN 0921-8181. https://dx.doi.org/10.1016%2Fj.gloplacha.2004.07.001
- Bruun, P. (1962). "Sea-Level Rise as a Cause of Shore Erosion". American Society of Civil Engineers Journal of the Waterways and Harbours Division 88: 117–130.
- Grilli, Annette; Spaulding, Malcolm L.; Oakley, Bryan A.; Damon, Chris (2017-04-19). "Mapping the coastal risk for the next century, including sea level rise and changes in the coastline: application to Charlestown RI, USA" (in en). Natural Hazards 88 (1): 389–414. doi:10.1007/s11069-017-2871-x. ISSN 0921-030X. https://dx.doi.org/10.1007%2Fs11069-017-2871-x
- Schwartz, Maurice (1967). "The Bruun Theory of Sea-Level Rise as a Cause of Shore Erosion". The Journal of Geology 75 (1): 76–92. doi:10.1086/627232. https://dx.doi.org/10.1086%2F627232
- Bruun, Per (February 1983). "Review of conditions for uses of the Bruun rule of erosion". Coastal Engineering 7 (1): 77–89. doi:10.1016/0378-3839(83)90028-5. ISSN 0378-3839. https://dx.doi.org/10.1016%2F0378-3839%2883%2990028-5
- Bruun, Per (1988-10-07). "The Bruun Rule of Erosion by Sea-Level Rise: A Discussion on Large-Scale Two- and Three-Dimensional Usages" (in en). Journal of Coastal Research 4 (4). ISSN 0749-0208. http://journals.fcla.edu/jcr/article/view/77813.
- Rosati, J.; Dean, R.; Walton, T. (2013). "The modified Bruun Rule extended for landward transport". Marine Geology 340: 71–81. doi:10.1016/j.margeo.2013.04.018. https://digitalcommons.unl.edu/cgi/viewcontent.cgi?article=1218&context=usarmyresearch.
- Zhang, Keqi; Douglas, Bruce C.; Leatherman, Stephen P. (May 2004). "Global Warming and Coastal Erosion" (in en). Climatic Change 64 (1/2): 41–58. doi:10.1023/b:clim.0000024690.32682.48. ISSN 0165-0009. https://dx.doi.org/10.1023%2Fb%3Aclim.0000024690.32682.48
- Dean, R.G.; Houston, J.R. (August 2016). "Determining shoreline response to sea level rise". Coastal Engineering 114: 1–8. doi:10.1016/j.coastaleng.2016.03.009. ISSN 0378-3839. https://dx.doi.org/10.1016%2Fj.coastaleng.2016.03.009
- Ashton, Andrew D.; Walkden, Mike J.A.; Dickson, Mark E. (June 2011). "Equilibrium responses of cliffed coasts to changes in the rate of sea level rise". Marine Geology 284 (1–4): 217–229. doi:10.1016/j.margeo.2011.01.007. ISSN 0025-3227. https://dx.doi.org/10.1016%2Fj.margeo.2011.01.007
- Hinkel, Jochen; Nicholls, Robert J.; Tol, Richard S.J.; Wang, Zheng B.; Hamilton, Jacqueline M.; Boot, Gerben; Vafeidis, Athanasios T.; McFadden, Loraine et al. (December 2013). "A global analysis of erosion of sandy beaches and sea-level rise: An application of DIVA". Global and Planetary Change 111: 150–158. doi:10.1016/j.gloplacha.2013.09.002. ISSN 0921-8181. https://zenodo.org/record/3418449.
- Davidson-Arnott, Robin G. D. (November 2005). "Conceptual Model of the Effects of Sea Level Rise on Sandy Coasts" (in en-US). Journal of Coastal Research 216: 1166–1172. doi:10.2112/03-0051.1. ISSN 0749-0208. https://dx.doi.org/10.2112%2F03-0051.1
- Neshaei, M. A. Lashteh; Ghanbarpour, F. (2017-05-26). "The effect of sea level rise on beach morphology of caspian sea coast" (in en). Frontiers of Structural and Civil Engineering 11 (4): 369–379. doi:10.1007/s11709-017-0398-6. ISSN 2095-2430. https://dx.doi.org/10.1007%2Fs11709-017-0398-6
- Lee, Hee Jun; Yi, Hi-Il (March 2018). "Seabed Gradient Controlling Onshore Transport Rates of Surf Sand during Beach Retreat by Sea Level Rise" (in en). Ocean Science Journal 53 (1): 133–142. doi:10.1007/s12601-017-0056-x. ISSN 1738-5261. https://dx.doi.org/10.1007%2Fs12601-017-0056-x
- Zhang, Xiaoling; Dai, Zhijun; Chu, Ao; Du, Jinzhou (2013-08-30). "Impacts of relative sea level rise on the shoreface deposition, Shuidong Bay, South China" (in en). Environmental Earth Sciences 71 (8): 3503–3515. doi:10.1007/s12665-013-2740-1. ISSN 1866-6280. https://dx.doi.org/10.1007%2Fs12665-013-2740-1
- Dickson, Mark E.; Walkden, Mike J.A.; Hall, Jim W. (2007). "Systemic impacts of climate change on an eroding coastal region over the twenty-first century". Climatic Change 84 (2): 141–166. doi:10.1007/s10584-006-9200-9. https://dx.doi.org/10.1007%2Fs10584-006-9200-9
- Grilli, Annette; Spaulding, Malcolm L.; Oakley, Bryan A.; Damon, Chris (2017). "Mapping the coastal risk for the next century, including sea level rise and changes in the coastline: application to Charlestown RI, USA". Natural Hazards 88: 389–414. doi:10.1007/s11069-017-2871-x. https://dx.doi.org/10.1007%2Fs11069-017-2871-x
- Houston, J.R.; Dean, R.G. (July 2014). "Shoreline Change on the East Coast of Florida" (in en-US). Journal of Coastal Research 296 (4): 647–660. doi:10.2112/jcoastres-d-14-00028.1. ISSN 0749-0208. https://dx.doi.org/10.2112%2Fjcoastres-d-14-00028.1
- Appeaning Addo, K.; Walkden, M.; Mills, J.P. (2008). "Detection, measurement and prediction of shoreline recession in Accra, Ghana". ISPRS Journal of Photogrammetry and Remote Sensing 63 (5): 543–558. doi:10.1016/j.isprsjprs.2008.04.001. https://dx.doi.org/10.1016%2Fj.isprsjprs.2008.04.001
- Vitousek, Sean; Barnard, Patrick L.; Limber, Patrick (2017). "Can beaches survive climate change?" (in en). Journal of Geophysical Research: Earth Surface 122 (4): 1060–1067. doi:10.1002/2017jf004308. ISSN 2169-9003. https://dx.doi.org/10.1002%2F2017jf004308
- Ranasinghe, Roshanka (2016). "Assessing climate change impacts on open sandy coasts: A review". Earth-Science Reviews 160: 320–332. doi:10.1016/j.earscirev.2016.07.011. ISSN 0012-8252. https://dx.doi.org/10.1016%2Fj.earscirev.2016.07.011
- Ranasinghe, Roshanka; Callaghan, David; Stive, Marcel (2012). "Estimating coastal recession due to sea level rise: beyond the Bruun rule". Climatic Change 110 (3–4): 561–574. doi:10.1007/s10584-011-0107-8. https://dx.doi.org/10.1007%2Fs10584-011-0107-8
- Atkinson, Alexander; Baldock, Tom; Birrien, Florent; David, Callaghan; Nielsen, Peter; Beuzen, Tomas; Turner, Ian; Blenkinsopp, Chris et al. (2018). "Laboratory investigation of the Bruun Rule and beach response to sea level rise". Coastal Engineering 136 (4): 183–202. doi:10.1016/s0378-3839(98)00043-x. ISSN 0378-3839. https://www.sciencedirect.com/science/article/pii/S0378383917302648.
- French, Jon; Payo, Andres; Murray, Brad; Orford, Julian; Eliot, Matt; Cowell, Peter (March 2016). "Appropriate complexity for the prediction of coastal and estuarine geomorphic behaviour at decadal to centennial scales". Geomorphology 256: 3–16. doi:10.1016/j.geomorph.2015.10.005. ISSN 0169-555X. https://dx.doi.org/10.1016%2Fj.geomorph.2015.10.005