Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is an old version of this entry, which may differ significantly from the current revision.
The article presents the rainfall threshold development framework and its employment for sediment-related disaster from Malaysia’s perspective. The open issues and challenges on deriving the rain threshold are discussed in details. The outcomes of this review could serve as references for the application in sediment-related disaster management worldwide, especially for developing countries.
- critical rainfall
- debris
- landslide
- mudflow
- hydropower
1. Introduction
Landslides, debris and mudflows (DMF), and rockfalls are types of sediment-related disasters whereby rainfall is the main triggering factor [1] The debris flow slide downslope under the influence of gravity consists of a mixture of coarse material, air and water to create a slurry and its ability to wash away anything along its path in high velocity depends on the slope gradient. Mudflow, also known as earth flow, contains at least 50% sand, silt and clay particles and the materials flow downslope rapidly. It is often referred to as a mud flood when the mixture reaches the equilibrium state, as well as when the landslide dam collapses. These sediment-related disasters occur in a sporadic and unpredictable manner. However, based on the extent, regularity and consequences of historical events, forecasting these phenomena has become a global subject of considerable interest. As Guzzetti et al. [2] defined, the rainfall threshold is the condition or amount of rainfall that is likely to initiate sediment-related disasters. Therefore, it is agreed that the rainfall threshold is the most significant tool to predict impending occurrences, and this has been enhanced to facilitate an adaptable and reliable prediction [3].
Referring to the work of Piciullo et al. [4], the rainfall threshold can be implemented as a warning model for landslide early warning systems (LEWS). LEWS are one of the passive countermeasures in the framework of landslide risk management at both local and regional scales [5]. Local LEWS (Lo-LEWS) are more specific in the monitoring of a single landslide at the slope scale, while territorial LEWS (Te-LEWS) monitor multiple sites at a regional scale.
The issues with and challenges of assessing the rain threshold for the alert, the forecast and the warning rain greatly concern the development of the landslide model. The effectiveness of the warning model also depends on the false alert rate and time for evacuation. Therefore, this kind of effective evaluation would only be possible once the warning model is well established with the specified or identified threshold. However, the hydrological threshold does not provide the spatial information and impact of the upcoming event.
In Malaysia, sediment-related disasters are associated with hilly and mountainous landscapes, coupled with intense or prolonged rainfall [6,7,8,9,10,11,12,13]. Figure 1 graphically summarizes the major disaster events recorded in Malaysian history. The first-ever massive landslip took place in 1961, which injured 35 people and claimed another 16 lives in Ringlet, Cameron Highlands. The 1996 debris flow incident in Keningau, Sabah, was perhaps the deadliest disaster with 302 recorded deaths and 4925 houses destroyed. The threat of landslides was further witnessed as recently as 2020, when three people were killed. Over the past decades, DMF and landslide disasters have occurred on a frequent basis with a total loss of more than 600 lives (Figure 1 and Table 1), and several research efforts have been carried out, focusing on the high-risk areas.
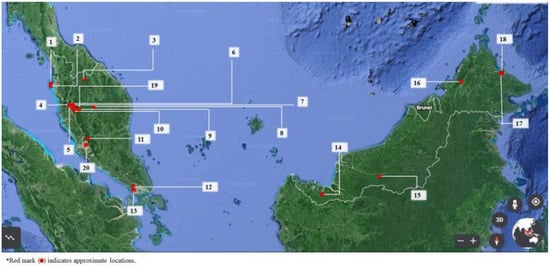
Figure 1. Location of sediment-related disaster events (involving death) in Malaysia.
Table 1. Details of the historical summary of sediment-related disaster events in Malaysia.
| ID No. | Date | Disaster Type | Location | Death | Injury | Cost (Million RM) |
Consequence |
|---|---|---|---|---|---|---|---|
| 1 | October 2017 | Landslide | Tanjung Bungah, Penang Island | 11 | NA | NA | NA |
| 2 | October 2018 | Landslide | Bukit Kukus Road, Georgetown, Penang Island | 9 | NA | NA | NA |
| 3 | 31 December 1993 | Landslide | KM 59.5, East-West Highway | 1 | 3 | NA | Damaged one car |
| 4 | October 1973 | Landslide | Kampung Kacang Putih, Ipoh | 42 | NA | 64.78 | NA |
| 5 | June 2020 | Landslide | Taman Silibin Indah, Ipoh | 1 | NA | NA | NA |
| 6 | December 2004 | Rock fall | Limestone hill in Bercham, Ipoh | 2 | NA | NA | Buried back portion of illegal factory at the foot of a limestone hill |
| 7 | November 2020 | Landslide | The Banjaran Hotspring Retreat, Tambun | 2 | NA | NA | NA |
| 8 | 24 October 1993 | Landslide | KM 58, Kuala Lipis-Gua Musang Road | 1 | 15 | NA | NA |
| 9 | 6 January 1996 | Landslide | North-South Expressway (NSE) near Tempurung Cave, Gopeng | 1 | NA | 6.7 | NA |
| 10 | 29 August 1996 | Mud slide | Pos Dipang Kg. Sahom, Kampar | 44 | NA | 69 | NA |
| 11 | 28 November 1993 | Landslide | Kuala Lumpur-Karak Expressway | 2 | NA | NA | NA |
| 11 | 30 June 1995 | Landslide | Kuala Lumpur-Karak Expressway | 20 | 22 | 48.3 | Damaged 10 cars |
| 12 | December 2001 | Debris flow | Pulai Mount, Johor | 5 | NA | NA | Washed away settlements along the river bank |
| 13 | 18 October 1996 | Landslide | Gelang Patah, Johor | 1 | NA | NA | Six people evacuated |
| 14 | 28 January 2002 | Shallow rotational slide | Simunjan, Sarawak | 16 | NA | 28 | Buried a number of houses |
| 15 | 26 December 2000 | Landslide | Kampung Baru Cina, Kapit, Sarawak | 2 | NA | NA | Buried two villagers, destroyed nine wooden houses |
| 16 | 26 December 1996 | Debris flow | Keningau, Sabah | 302 | NA | NA | Wiped out several villages, destroyed 4925 houses |
| 17 | January 1999 | Shallow rotational slide | Squatters settlement, Sandakan, Sabah | 13 | NA | NA | Buried a number of house/huts |
| 18 | 8 February 1999 | Landslide | Kampung Gelam, Sandakan, Sabah | 17 | 2 | NA | Destroyed four houses |
| 19 | 1 May 1961 | Massive landslip | Ringlet, Cameron Highlands | 16 | 35 | 3.48 | |
| 19 | 4–7 December 1994 | Landslide | Cameron Highlands | 7 | NA | NA | |
| 19 | 24 October 1995 | Landslide | Tringkap, Cameron Highlands | 1 | NA | NA | Damaged one house |
| 19 | December 1995 | Landslide | Cameron Highlands | 7 | NA | NA | Damaged a few houses |
| 19 | 9 October 1996 | Landslide | Terla, Cameron Highlands | 3 | 2 | NA | Damaged a few houses |
| 19 | 9 January 2000 | Debris flow | KM 81.6, Tanah Rata—Brinchang Road | 6 | NA | NA | Washed away worker squatters |
| 19 | April 2006 | Landslide | KM 33, Simpang Pulai Road | 35 | NA | 4.6 | |
| 19 | 23 October 2013 | Mud flood | Bertam Valley, Cameron Highlands | 3 | Damaged 80 houses | ||
| 20 | December 2008 | Landslide | Bukit Antarabangsa, Hulu Kelang | 4 | 15 | NA | NA |
| 20 | 6 December 2008 | Landslide | Taman Bukit Mewah, Ampang | 5 | 7 | 7.6 | Damaged 14 bungalows |
| 20 | 22 May 2011 | Landslide | FELCRA Semungkis, Hulu Langat | 16 | NA | NA | NA |
| 20 | 11 December 1993 | Landslide | Highland Tower, Taman Hillview, Hulu Kelang | 2 | 184 | NA | Collapse of one block of a 12-storey high apartment |
| 2 May 1994 | Landslide | Puchong Perdana | 3 | NA | NA | 10 families evacuated | |
| 20 | 11 May 1997 | Landslide | Pantai Dalam, Kuala Lumpur | 2 | 4 | NA | 19 families evacuated |
| 20 | 15 May 1999 | Landslide | Bukit Antarabangsa, Hulu Kelang | NA | NA | 5.4 | 1000 people evacuated |
| 20 | 22 September 2001 | Landslide | Sg. Chinchin, Gombak | 1 | NA | NA | Partly destroyed one house |
| 20 | 20 November 2002 | Landslide | Taman Hillview, Ampang | 8 | 5 | 17.4 | Damaged one bungalow |
| 20 | November 2003 | Rock debris | New Klang Valley Expressway (NKVE) | 8 | NA | 36 | Expressway closed for more than 6 months |
| 20 | November 2004 | Debris flow | Taman Harmonis, Gombak | 1 | NA | NA | NA |
| 20 | 31 May 2006 | Landslide | Kampung Pasir, Hulu Kelang | 4 | NA | 21 | Damaged three blocks of longhouses |
2. Rainfall Threshold
A warning model for LEWS can be based on physical or empirical models. The empirical model is mainly based on the correlations between rainfall events that have caused landslides [14], whereas the physical method involves physically computing the force balance between shear-force and shear-force resistance at each slope. Papa et al. [15] highlighted that the established physical model requires instrumentation to compute certain inputs such matric suction within the soil layers, hydraulic conductivity, soil moisture and pore water pressure. It also includes the infinite slope stability analysis, of which the main parameter is the groundwater table that, when fully saturated, leads to failure. Therefore, the physical-based model is highly suitable for a site-specific slope, but it is very costly if one has to apply it to the regional threshold. The conceptual model is also considered as a process-based model that represent the physical analogy, representing the quantitative understanding between rainfall and landslides. It is more widespread than the instrumentation installation requirement. The example of the conceptual model is the leaky barrel model [16] and the soil water index (SWI) [17,18]. On the other hand, the work of Yamazaki et al. [19] has successfully identified the critical rainfall condition to simulate the disaster temporally and spatially. The advantage of this method is that it takes into account that the event may occur during the observation with no rain forecast. The rainfall condition curve is segregated according to their slope classification or spatial condition when the current rainfall condition breaches the curve, hence indicating when the disaster is likely to occur.
While the empirical model is more widespread, the application of empirical rainfall thresholds has been in place since 1987, with many studies conducted in many countries, especially in Italy, and central and southern Europe [20]. There are several types and characteristics of rainfall thresholds, namely the intensity–duration (I-D), accumulated rainfall–duration (E-D), intensity–accumulated rainfall (I-E), accumulated rainfall–accumulated rainfall (E-E) and antecedent or working rainfall or rainfall index. The most common and pioneering is the I-D threshold established by Caine [21] Most of the threshold correlating the rainfall characteristic to landslide events is presented in terms of the power law relationship [22]. The main goal in the empirical model development is to identify the rain that has triggered the disaster despite other additional factors, if present. Therefore, the definition of rainfall intensity plays the most crucial part in this manner [23]. Rainfall intensity refers to the rainfall depth over a certain duration, depending on the observation period. The timescale is normally in an hourly format [3]. For a short period, it may represent the current intensity of the rainfall during the occurrence of the disaster. Likewise, for a long period, it may represent the average value of the rainfall over hours, i.e., 2, 3 or 24 h. The definition should be consistent during the construction of the numerical rainfall characteristic of the historical events, and the forecasting rainfall (forecasting events) and the observed rainfall (monitoring events). Due to the diversity of the definition, one should state clearly the definition of rainfall intensity in their work for others to compare and adopt the method accordingly. The disaster is likely to occur when the current rainfall characteristic based on the observed rainfall data (or real-time data) are beyond the rainfall characteristic that resulted in the disaster in the past, referred to as the rainfall threshold. The framework is adopted in the early warning system as a warning model that the impending disaster can be forecasted, in order to alert the respective stakeholder (authority or community). Figure 2 illustrates the conceptual description of the I-D threshold under ideal conditions, where there is a clear separation between the sediment-related disaster-triggering and non-triggering rainfall conditions [24].
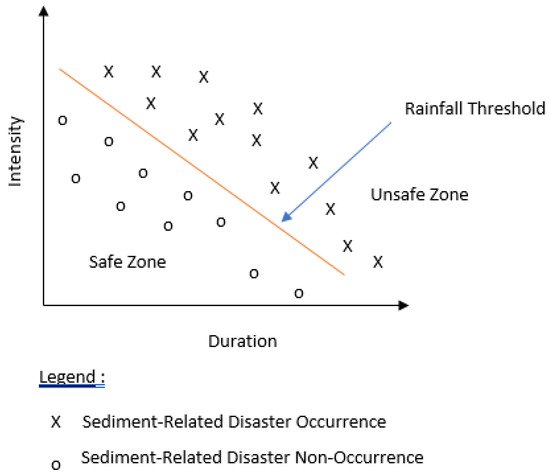
Figure 2. Conceptual description of intensity–duration of rainfall threshold under ideal conditions [24].
Both the physical and empirical model are significant and can be used as warning models employed in any early warning system in order to reduce the disaster risk. However, the chosen model should be tailored according to the local environment, climate and geological condition of the area under surveillance. Since sediment-related disaster is caused by many factors—either spatial or climatic factors and types of behavior—it is pertinent to compile all of the important information related to the possible causes [25]. In general, the process or step of the threshold development is illustrated in the figure below.
Based on Figure 3, the general steps of rainfall threshold development are as follows: firstly, the collection of the dataset features. This process includes the landslide data inventory and the determination of the rainfall data source. The catalogue of the data should be accurate or almost accurate, including items such as the date, time, type of landslide, the location and the data source. Other information such as the slope gradient, topography and lithology and details of the landslide are essential for analysis and comparison. The selection of rainfall data is very crucial as it is correlated with the risk of landslide. Therefore, details on the criteria of the rainfall data to be used in the analysis are very important. The method of criteria selection of rainfall data such as a single reference, manual/expert judgement, the reference rain gauge, the nearest rainfall station and the Theisen polygon method should be specified clearly in the study [3]. The rainfall parameter that governs the relationship of the landslide is determined, whereby the governing parameter is considered to be the causal rain. Next is the identification of the threshold. The outcome of this step is the established relationship between the causal rain and the disaster with the threshold line. This process requires the modeler to draw the separation line and once it is breached, the disaster is likely to occur. Therefore, the drawn line is very subjective; if it is too conservative then the warning could be missed; on the contrary, if it is too low then it could end up resulting in a false alarm. The practical method, as suggested by Nikolopoulos et al. [24], is based upon visual observation of the modeler to separate the safe zone and unsafe zone at the heuristic lower boundary of the empirical data. Another method is based on the frequentist method [26]. Lastly, is the validation of the model. This step is categorized into two parts. Firstly, is the model validation and secondly, is the model performance. In order to reach the second category, the model should be implemented or applied in the early warning system. As per the first category, there is no standard method in place worldwide as yet, but Segoni et al. [3] suggested that the validation can be made using the same dataset or independent datasets. The warning model is not static but has a dynamic manner.
This entry is adapted from the peer-reviewed paper 10.3390/w14203212
This entry is offline, you can click here to edit this entry!
