Solid-state argyrodite electrolytes are promising candidate materials to produce safe all-solid-state lithium batteries (ASSLBs) due to their high ionic conductivity. These batteries can be used to power electric vehicles and portable consumer electronics which need high power density. Atomic-scale modeling with ab initio calculations became an invaluable tool to better understand the intrinsic properties and stability of these materials. It is also used to create new structures to tailor their properties. This review article presents some of the recent theoretical investigations based on atomic-scale modeling to study argyrodite electrolytes for ASSLBs. A comparison of the effectiveness of argyrodite materials used for ASSLBs and the underlying advantages and disadvantages of the argyrodite materials are also presented in this article.
- argyrodite electrolyte
- all-solid-state lithium batteries
- modeling
- molecular dynamics
- simulation
1. Introduction
Argyrodite electrolytes are very promising solid-state electrolytes (SSE) materials for all-solid-state batteries (ASSB). The high lithium mobility and conductivity in argyrodite electrolytes make it a potential solution for ASSBs [1]. The SSE also allows more effective cell packaging accompanied by their high gravimetric/volumetric energy density applications [2]. Lithium batteries with liquid organic electrolytes [3] have protection issues in terms of high combustibility and electrolyte leakages, while those with SSE are precisely contrary to these qualities [4–7]. Recently, Zhou et al. [8] have researched the electrochemical performance of Li6PS5Cl in an ideal solid-state battery (SSB). It exhibited sublime performance as its ionic conductivity is improved through the initiation of Li vacancies and disorder and showed congruence between cells. Some research works have been conducted to improve the activity of lithium-ion batteries, such as elastic stiffening tendency to increase stresses to aggrandize lithium-ion diffusion and uphold the elastic modulus. [9]
Considering the SSEs, everything is not perfect. The electrolyte interfaces with both cathode and anode require significant considerations such as the restraint of the common boundary developed at the borderline of the cathode [10,11] and the anode [12,13]. Malleable solid electrolytes having an appropriate Young’s modulus can repress the growth of lithium dendrite for lithium anode and enhance finer connection upon cycling when taken with the cathodic substance [3,14]. However, an established scalable route to such material is a substantial challenge that could limit the progress of the SSB field because of simple economics. [8]
The investigation of the conductivity of SSE is an involved experiment because of the problem in the reproduced reformation of the materials and the responsivity of the conduction property. Computational approaches often utilize a measure for the determination of conductivity depending on the configuration and constituents of crystal-like substances. In computational analysis, researchers have critically controlled these variables, unlike empirical analyses in the presence of dopants and flaws, which are susceptible to the manufacturing environments and hard to describe. To address issues relating to the initiation of force fields for processes in which charge transfer and polarizability are applicable, ab initio molecular dynamics (MD) simulations are of interest, and scholars have broadly utilized them. However, due to the somewhat low conductivity of SSE materials (always not up to 10−3 S.cm−1), it is frequently computationally expensive, besides being somewhat impractical, to essentially quantify the estimation of the conductivity of the materials considered in ambient condition by means of ab initio MD computations [15,16]. An approach to resolve this difficulty is to compute the coefficient of diffusivity at elevated temperatures and then apply the Arrhenius equation to speculate the ionic diffusivity at ambient temperature [15,17]. Meanwhile, scholars expect the relative errors in the eventual conductivity value to be substantial, since the high-temperature data for statistical errors engender more relative errors for such estimated values [15]. So, they need to introduce proxy computational approaches which give definitive approximates of the diffusion coefficient to review the processes. Researchers have reported that ab initio non-equilibrium molecular dynamics (AI–NEMD) simulations is useful in this premise. Although they used AI–NEMD simulations for the ionic conductivity of LiBH4 in a review [18], they did not juxtapose the outcome of that review with that from ab initio equilibrium molecular dynamics (AI–EMD) simulations. So, it is demonstrated that AI–NEMD simulations permit good estimates for the coefficients of diffusivity acquired for materials with diffusivities not precisely ascertained by AI–EMD computations [19]. They used these values to establish materials such as SSE for recognizing the objective for modifications in experimentations.
An argyrodite structure (for example, Li6PS5Cl) is a cubic crystal structure possessing F43 m, space group number 216 [20,21]. The literature have examined argyrodite supercell assumed from two-unit cells each containing four Li6PS5Cl, with 104 atoms (eight simple unit cells) for the entire computations of the argyrodite material. The regulation of the unit cell lattice parameters was conducted through energy minimization, so the dimension is 10.08 Å × 10.08 Å × 10.08 Å (Å = Angstrom). From Figure 1, Li-ions fill 48 h Wyckoff positions, where there is a distribution of S atoms on 4a and 4c sites. Again, there is an attachment of S in the 4a areas to the P atoms (4b areas) framing (labeled S1), surrounded by Li-ions is the S as S2- in 4c sites (labeled S2), so the Cl– also get dispersed in 4a sites. There is a formation of pure and defective Li6PS5Cl structures gleaned from its space lattice. When discussing the creation of the Li5PS4Cl2 structure, it is crucial to replace the S2 S ions with Cl ions and achieve charge balance by removing one of the lithium-ions from the structure surrounding each individual S2 [21].
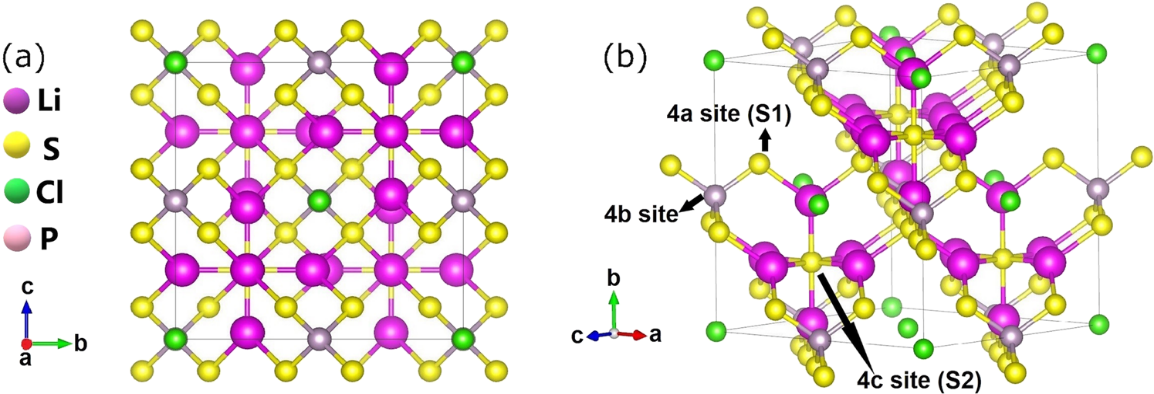
Figure 1. Sample of Li6PS5Cl lattice structure. Purple = lithium, yellow = S, green = Cl, and light purple = P atoms (at the middle of the ion). Adapted from Baktash et al. [19].
In Sections 2–4, we explain the general modeling approaches for argyrodite materials. They also contain comparisons of common argyrodite compounds. Sections 5 and 6 are for some particular argyrodite compounds of high interest amongst researchers due to their electrochemical properties. Ab initio molecular dynamics modeling specifics and machine learning for the argyrodites are presented in Section 7. Sections 8 and 9 are for discussions and conclusions. Therefore, this work reviews the previous work conducted on the modeling of argyrodite electrolytes materials with machine learning (ML) predictive models as speculating the utilization of lithium as a peculiar cathodic substance.
2. Modeling of Argyrodite Materials
The determination of diffusion coefficients of argyrodite materials is essential; however, it is relatively problematic. The diffusion coefficients are calculated using AI–NEMD and AI–EMD simulations for the high diffusive SSE to illustrate an obtained precision. Moreover, the AI–EMD is terribly slow to investigate diffusion coefficients, whereas it is viable and timely to get them using AI–NEMD simulations. Therefore, utilizing AI–NEMD simulations for the coefficient of diffusivity of Li-ions in argyrodite materials (Li6PS5Cl and Li5PS4Cl2), Baktash et al. obtained two potential electrolytes for ASSB [19]. These computations prove Li-ions diffusion coefficient in Li5PS4Cl2 is greater than other promising SSEs, making it bespoke for future technologies. Small disorders and voids were considered as possible explanations for the variability observed in experimental data. Remarkably, inculcating Li vacancies and disarray into the system tends to improve Li6PS5Cl ionic conductivity.
Again, amongst the ASSBs, sulfide-based electrolytes, as a result of their being electrochemically stable, noble mechanical characteristics and ionic conductivities are one of the promising candidates, more so than other probable SSEs [22–25]. The Li-argyrodites are built on Li7PS6, possessing substantial ion conductivities of 10−5–10−3 S.cm−1 under ambient condition [26]. Considering the lithium-argyrodites model peak temperature point, its ionic conductivity as well, is higher at an elevated temperature point, high conductivity argyrodite models, such as Li7PS6, are unstable at ambient temperature. The literature reported that the creation of lithium vacancies and institution of halogens into the Li7PS6 model make it possible to produce configurations of Li6PS5X (X = Cl, Br, and I) [1] which are constant at ambient temperature with higher conductivity [27,28]. Empirical reports prove Li6PS5X (X = Cl, Br, and I) to possess identical lattice configurations of space group, F̅43m, with Li7PS6. As a matter of fact, Li6PS5Cl and Li6PS5Br ionic conductivities at ambient temperature are sufficiently high for battery technology [29,30]. Moreover, halides disorder effects are researched [28] as investigations prove that Li6PS5Cl have an ionic conductivity of about 10−3 S.cm−1 at ambient temperature and electrochemical stability up to 7V versus Li/Li+ [3,30,31]. Computations have suggested that more halogens and Li vacancies give rise to greater ionic conductivities, and it is speculated that Li5PS4Cl2 could be a replacement [21]. Many experimental and computational overviews have been conducted for Li6PS5Cl, but because of numerous difficulties, there is not enough full absolute knowledge of the mechanism of the diffusivity of this specimen, and the conjecture for its conductivity varies over many orders of magnitude [16–17,21,27,30–32]. Researchers have reviewed a lot of superionic materials to be potentially lithium solid electrolytes [33,34]. While oxides and phosphates are inelastic and stiff, Li3PO4 [3] tend to be flexible, simply formed, and densified, with modulus of rigidity reduced 5 to 10 times [35,36], showing good ionic conductivity of about 25mS·cm−1 at ambient temperature [37-–46].
Amongst the phases provide in Table 1, the last-mentioned phase is considered the most stable in connection with lithium metal, since a phase consisting of Li2S [1], Li3P and LiX (X = Cl, Br) develops at a relatively low order when in connection with the lithium that works as an in situ passivation interphase [47]. Some innovative ASSBs cells utilized lithium-argyrodite as SSEs accompanied by various cathodic and anodic arrangements [30,48–54]. Nonetheless, scientists have designed all the Li-argyrodite electrolytes investigated so far, and their modeling is performed by a conventional mechanical milling machine followed by the application of heat. Ball-milling exudes substantial energy and makes the synthesis hard to measure and thereby not feasible to SSB formation. Solution-engineered processes did not alone solve these issues, but improbably it also decreases the ensuing temperature of the heat treatment coupled with time. Solution-based methods were engineered for Li4PS4I [55], β-Li3PS4 [1,56], Li7P2S8I [57], and Li7P3S11 [58] structures, alongside differing levels such as the purity of the phase and ionic conductivity of the result. The literature delineated Li6PS5Cl argyrodite, requiring a dissolution−reprecipitation procedure arising out of a solution of ethanol [32]. While mechanical milling measure is essential, as the ionic conductivity of the specimen reported is 1.4 × 10−2mS·cm−1, which is two orders of magnitude less than the traditional solid-state formation technique, an exact and valid “all-solution” argyrodite Li6PS5X formation stands out as a question.
Table 1. Lithium superionic conductor phase [1,8].
|
Phase |
Ionic Conductivity (IC) (mScm−1) |
Activation Energy (Ea) (eV) |
Reference |
|
Li3.25Ge0.25P0.75S4 |
2.2 |
0.21 |
|
|
Li10GeP2S12 |
12 |
0.25 |
|
|
Li9.54Si1.74P1.44S11.7 |
25 |
0.24 |
[41] |
|
Li7P3S11 |
17 |
0.18 |
|
|
Li6PS5X (X = Cl, Br) |
∼1 |
0.3−0.4 |
Reprinted (adapted) with permission from ACS Energy Lett. 2019, 4, 1, 265–270 [8]. Copyright 2018 American Chemical Society.
It was shown that a direct solution-engineered procedure of Li6PS5X (X = Cl, Br, I) argyrodite [1] as well as Li6−yPS5−yCl1+y SSEs possess good lithium-ionic conductivities, which is about 2.4mS·cm−1, with reference to ambient temperature against chlorine and bromine phases. Ionic conductivity is more for an integrated Cl and Br, and chlorine-full phases, yielding about 4mS·cm−1.
3. Single Halides Argyrodites
The articulation in Kraft et al. [28] proves that solid-state engineered Li6PS5Cl and Li6PS5Br show an exact bulk of LiX and Li3PO4 dopants. Yubuchi et al. [59] reported the results culminating from the composite synthesis showing a more dopant level, attributed to the reactivity of ethanol and units, or slight moisture in the ethanol. Zhou et al. [8] used a related solution synthesis approach to produce a pure Li6PS5I phase with an imprint of lithium thiophosphate (Li3PO4) impurity, albeit with Li6PS5I argyrodite low ionic conductivity, which agrees with reviews from Pecher et al. [60]. However, the iodide crystallization explains a wide relevance of this solution synthesis procedure to the lithium-argyrodite species. Researchers represented the SEM images of grounded Li6PS5X (X = Cl, Br) materials to interpret the densified characteristics of the crystallite masses, and when processed into ASSB, they become incredibly useful [8]. Highly ductile sulfide solid electrolytes give good contact at the grain boundaries than oxides (which are always essentially brittle), even pressed parts without consideration of sintering result in multiple solid electrolyte phases [43]. The reported solution engineered ionic conductivities of Li6PS5X SSEs were determined by electrochemical impedance spectroscopy (EIS) in (stainless steel = SS) SS/Li6PS5X/SS arrangement at ambient temperature. Researchers reported the resistivities, 46 and 34 Ohm, for Li6PS5Br and Li6PS5Cl at ambient temperature, making the total conductivities 1.9 mS.cm−1 and 2.4 mS.cm−1, discretely. These values correspond with that of solid-state engineered Li6PS5Br and Li6PS5Cl argyrodites of about 1 mS·cm−1 and 3 mS·cm−1 apiece [28,31,46]. This shows that the dopant effects in the processed materials do not lower the Li-ions conductivity in the exceptionally fine electrolytes. It is noteworthy that these elements are especially improbable to enhance the gross ionic conductivity as the densified solid electrolyte pressed pieces enable good interaction amid Li6PS5X lattices and allow ample lithium ion straining pathways for transport [28]. Iodide argyrodite conductivity was reported to be 2 × 10−3 mS·cm−1, which tallies with the low values often published for this phase (i.e., 4 × 10−4 mS·cm−1) [60]. There is the measurement using a direct current (DC) polarization for the electronic conductivities of the two materials (Li6PS5Cl and Li6PS5Br) of the SS/ Li6PS5X/SS symmetric cells at ambient temperature. Zhou et al. [8] estimated the direct current electronic conductivities as 5.1 × 10−6 mS·cm−1 for Li6PS5Cl and 4.4 × 10−6 mS·cm−1 for Li6PS5Br. Both values are six orders of magnitude smaller than their individual ionic conductivities. Proving that Li6PS5Br and Li6PS5Cl argyrodite electrolytes obtained from synthesis are productively unalloyed ionic conductors.
4. Mixed Halide Argyrodites
Formerly researched mixed halide argyrodites Li6PS5X (X = Cl0.75Br0.25, Cl0.5Br0.5, and Cl0.25Br0.75) present substantial ionic conductivities when contrasted with single-halide phases [28], enabling the study of the molecular modeling of argyrodites. Zhou et al. [8] further showed the X-ray diffraction (XRD) patterns after heat treatment for the product, as the identical values reported for the single halide composition, especially the pure argyrodite phase, is available as an important crystalline phase with the presence of dopants of Li3PO4, Li2S, and LiX (X = Cl, Br). Additionally, the lattice parameters from Rietveld refinements increase directly from x = 0–1 in Li6PS5Cl1−xBrx. For solid solutions, as explained by Vegard’s principle, the disordered Cl/Br ions were constructed in the model, which demonstrates the argyrodite phases. They used EIS to measure the ionic conductivities and recorded an ionic conductivity of 3.9 mS·cm−1 for Li6PS5Cl0.5Br0.5, and using a DC polarization, they reported particularly low electronic conductivities. The ionic and electronic conductivities are summarized in Table 2.
Table 2. Compendium of the ionic and electronic conductivities of lithium-argyrodites primed by synthesis method [1,8].
|
S/N |
Material |
IC (mS·cm−1) |
EC (mS·cm−1) |
|
1. |
Li5.5PS4.5Cl1.5 |
3.9 |
1.4 × 10−5 |
|
2. |
Li5.75PS4.75Cl1.25 |
3.0 |
2.6 × 10−5 |
|
3. |
Li6PS5Br |
1.9 |
4.4 × 10−6 |
|
4. |
Li6PS5Cl0.25Br0.75 |
3.4 |
1.1 × 10−5 |
|
5. |
Li6PS5Cl0.5Br0.5 |
3.9 |
1.4 × 10−5 |
|
6. |
Li6PS5Cl0.75Br0.25 |
3.2 |
3.7 × 10−6 |
|
7. |
Li6PS5Cl |
2.4 |
5.1 × 10−6 |
Reprinted (adapted) with permission from ACS Energy Lett. 2019, 4, 1, 265–270. Copyright 2018 American Chemical Society.
Previously reported density functional theory (DFT) MD simulations further increased the Li ion conductivity through the sulfur/halide ratio adjustment [21], shown by the XRD scales of Li5.75PS4.75Cl1.25 and Li5.5PS4.5Cl1.5 formulated by the solution-engineered synthesis approach. Lithium-argyrodite electrolytes are available as the prime products, with dopants of Li3PO4 contrasted with Li6PS5X, little Li2S and carefully selected LiCl. EIS reported surging ionic conductivities with a greater Cl-to-S ratio for Li5.75PS4.75Cl1.25 and Li5.5PS4.5Cl1.5, respectively (see Table 2). The incremental ionic conductivities and XRD scale show a replacement of S with Cl, introducing Li-ions voids for the argyrodite structure, thus enhancing the ionic conductivity. However, because of the homogeneous array and X-ray smattering conditions of S and Cl, advanced neutron divergence work are important to differentiate the order of S/Cl disarray, Li vacancies and positioning in the argyrodite processes.
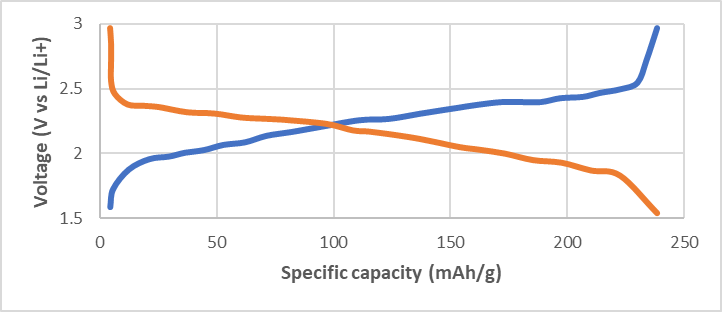
Again, Zhou et al. [8] considered TiS2/Li11Sn6 ASSBs prototype using Li6PS5Cl as an SSE formulated between 1.5V and 3.0V vs. Li/Li+ at 30 °C. Obviously, these cells utilized lithium alloy as a negative electrode due to their toughness with the goal of measuring the qualities of argyrodite. Prospects will make use of lithium as a discrete cathodic substance. Figure 2 presents two discharge−charge voltage depiction for Li6PS5Cl cells formed through the traditional solid-state approach (Figure 2a) and the solution-synthesized process (Figure 2b).
|
(a) |
|
(b) |
Figure 2. Comparison of Li6PS5Cl ASSB by (a) solid-state procedure (b) solution-synthesized procedure of TiS2/Li6PS5Cl/Li11Sn6 cells at current density, 100 μA.cm−2 (equivalent to 0.11charge rate). Reprinted with permission from ACS Energy Lett. 2019, 4, 1, 265–270.
The Li6PS5Cl cell produced by the solution-synthetic method presents an ideal capacity of 239 mAh.g−1 and presents no change from cells making use of derived SSE, suggesting that the slight scum produced within the solution-synthesized pathway are negligible in comparison with the overall performance of the cell.
5. Ionic Conductivity of Li5PS4Cl2
Utilizing AI-EMD and AI-NEMD simulations at 300 K, 600 K, 800 K, and 1000 K, the diffusion coefficient for Li5PS4Cl2 could be calculated. So, this process advances a specific collation with the accuracy of AI-EMD and AI-NEMD techniques and with extrapolated calculation at 300 K using the Arrhenius equation. There is an assessment of the AI–EMD simulations at 300 K, 600 K, 800 K and 1000 K for 45 ps, 40 ps, 20 ps and 20 ps, discretely. Researchers have calculated the MSD [16] of the Li-ions, values for ten models, and statistical errors at various temperatures using the results of these AI-EMD simulations. They examined the trajectories in each case to ensure that the simulation times (450 ps–200 ps) were enough to distinguish the Li-ions diffusion further from their starting points. Figure 3a–c show the MSD of the lithium-ions with time dependence at 300 K, 600 K and 800 K for the ten separate trajectories. In a diffusive motion, the MSD heightens with time, and the gradient is associated with diffusion co-efficient from Equation (1) [61].
|
(See nomenclature for terms definition.)
Figure 3d–f show the derivation of the MSD of 10 models involving the error bars where the coefficients of self-diffusion and the proportion of the conductivity of the material with an approximate computational accuracy. While noticing diffusive behavior, the value of the MSD at 35 ps at 300 K is only about 6 . The conductivity and coefficient of self-diffusion values are shown in Table 3, respectively.
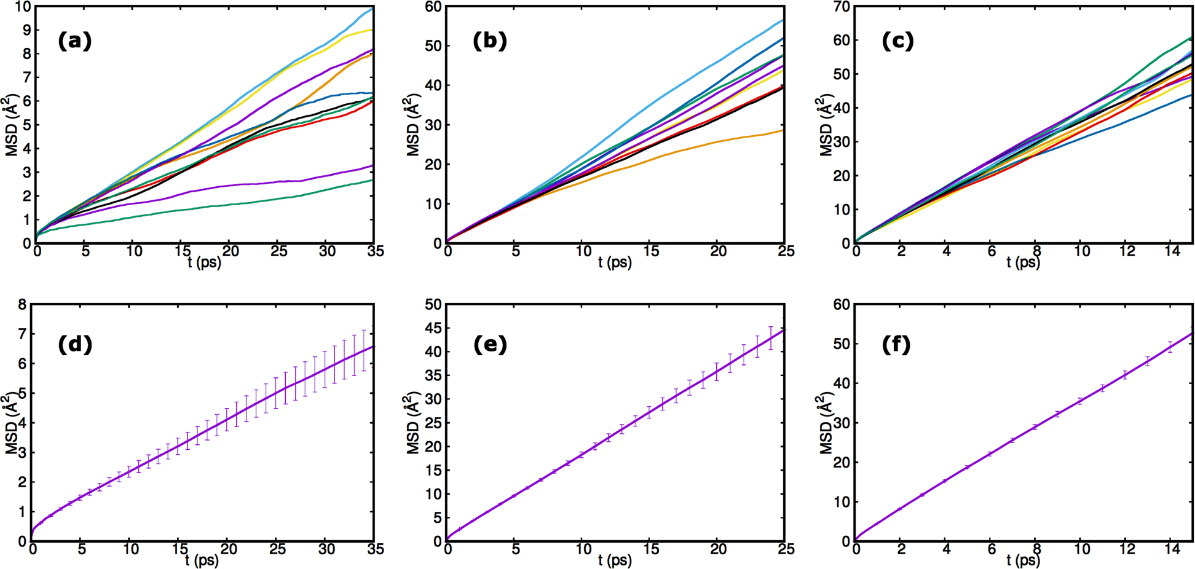
Figure 3. Lithium-ions mean square displacement (MSD) with time. Results for ten iterative computations of Li5PS4Cl2 at (a) 300 K, (b) 600 K, (c) 800 K, and MSD of the ions with respect to time with the error bars for ten iterative simulations considering (d) 300 K, (e) 600 K, (f) 800 K. Adapted from Baktash et al. [19].
Table 3. Computation using AI–EMD and AI–NEMD simulations for self-diffusion coefficient with concurrent conductivity of Li5PS4Cl2 at specific temperatures.
|
Temp. (K) |
AI–EMD |
AI–NEMD |
||
|
Ds (cm2 s−1) |
σ (S.cm−1) |
Ds (cm2 s−1) |
σ (S.cm−1) |
|
|
300 |
2.9 × 10−6 |
0.35 |
3.3 × 10−6 |
0.4 |
|
600 |
2.9 × 10−5 |
1.80 |
2.9 × 10−5 |
1.8 |
|
800 |
5.6 × 10−5 |
2.50 |
5.2 × 10−5 |
2.4 |
|
1000 |
8.9 × 10−5 |
3.20 |
8.9 × 10−5 |
2.9 |
Adapted from Baktash et al. [19].
For SSEs with minimal conductivity, such as those of about 10−3 S.cm−1 or less at ambient temperature, it is complex to compute an accurate conductivity at ambient temperature with ab initio simulations. In order to find a solution, it was specified that the conductivity of the material at peak temperatures may be calculated using a straightforward method, and that the values for the ambient temperature can be extrapolated to produce an approximation of the conductivity value. [18,61,62]. An Arrhenius representation for the conductivity of Li-ion data computed from AI-EMD simulations in Li5PS4Cl2 from MSD for various temperatures is illustrated by Figure 4.
From MSD [17] computations, the ionic conductivity of Li5PS4Cl2 at 300 K is 0.35 ± 0.05 S.cm−1. Figure 4 presents a close look into the values at 600 K and 800 K, the extrapolated conductivity presents an ionic conductivity ranging from 0.17–0.37 S.cm−1 at 300 K. This works well with the computed results. However, the statistical error for the elevated temperature values is minute when related to the results. Moreover, correlative error at decreased temperature is sizeable because of their extrapolated values. Additionally, the extrapolated result at 1000 K gave values from 0.17–0.33 S.cm−1 at 300 K, thereby realizing a minimal swap through an extra-elevated temperature since it requires a substantial temperature difference to advance a discrete value in the temperature reciprocal.
Aeberhard et al. [18] employed an alternate method based on AI-NEMD simulations to calculate the self-diffusion coefficient of hexagonal LiBH4 at 535 K, which is different from the method used in ab initio simulations to find the IC of SSE. To prove the accuracy of Baktash et al. [19], AI–NEMD simulations approach is employed to speculate the Li5PS4Cl2 coefficients of self-diffusion and conductivities at 300 K, 600 K, 800 K and 1000 K, so these values are juxtaposed with those from AI–EMD MSD calculations.
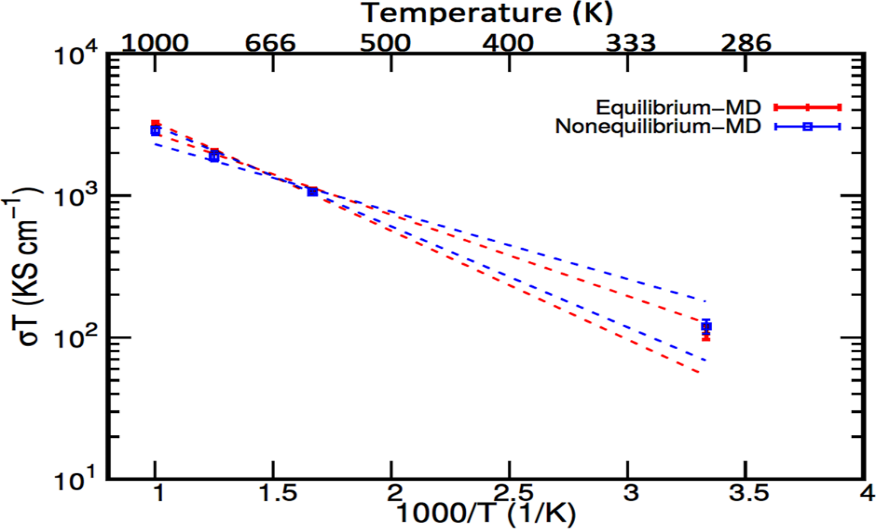
Figure 4. Arrhenius plot for Li5PS4Cl2 conductivity. Outcomes of AI–EMD simulations and AI–NEMD simulations at specific temperature. The error ranges for extrapolation estimated data at 600 K and 800 K to 300 K are displayed by AI-EMD and AI-NEMD, respectively. Adapted from Baktash et al. [19].
Calculating conductivity at various fields is necessary to identify the linear response domain for ionic conductivities calculations from AI-NEMD simulations. The EMD and NEMD procedures reported results work in the range of one standard error. There is an evaluation of the conductivity of the extrapolated specimen at 300 K from elevated temperatures. Distinguishing the lines in Figure 4 using comparable complete simulation times at 300 K, 600 K and 800 K for the NEMD and EMD computations, the NEMD simulations statistical errors values equate that of EMD approach. This is true for both direct consideration and extrapolated elevated temperatures values at 300 K.
Li5PS4Cl2 Collective Diffusion Coefficient
Scholars used the Nernst–Einstein models to connect the conductivity of a material to its coefficient of self-diffusion. However, if the sample of interest diffusing atoms tends to be stationary at the time of diffusion, on top of that, it is an ineffective estimation, and therefore, it is advisable to use the coefficient of collective diffusion [63]. When the diffusing atoms transpose individually, the coefficients of self and collective diffusion coincide, but they diverge when they do so collectively.
|
(2) Please see equation in the published paper |
(See nomenclature for terms definition.)
In order to determine if this calculation is adequate for the systems under consideration, Evans et al. [61] computed the Li5PS4Cl2 coefficient of collective diffusion using Equation (2) and compared it to the coefficient of self-diffusion. They picked the most diffusive pure system because it is challenging to make deductions when the statistical error is considerable, and since this statistical error for its collective diffusion computation is substantially higher than that of self-diffusion estimations. A report from Baktash et al. [19] compares the MSD discrete sample simulations for Li5PS4Cl2 at 800 K for the ions and their center of mass, but the error bar for the ion MSD remained low. This holds true since each ion in the sample can offer an autonomous contribution towards MSD. Therefore, the MSD (self and collective diffusion coefficients) computed in both ways agree. The agreement aligns with individual performance of the entire lithium-ions in Li5PS4Cl2 during the diffusion process, making it easy to compute the conductivity by the coefficient of self-diffusion.
6. Li6PS5Cl Ionic Conductivity
Keil et al. [64] reported that for diffusive motions, simulation times vary inversely with the coefficient of diffusion. For low conductivity models, such as EMD simulations, it is hard to obtain precise values, and at some points, there is no activity of ions in a practicable timescale between the areas in the electrolyte.
An analysis of Li5PS4Cl2 has shown that valid findings were achieved by coalescing NEMD computations under elevated temperatures with assumed values at minimal temperatures. So, a method of sustaining the range of materials to compute the conductivity by providing an approach of when the conductivity is very minimal to allow the use of EMD simulations has been reported. Baktash et al. [19] proved this tender by computing Li6PS5Cl ionic conductivity by NEMD simulations. Scientists have utilized both AI–EMD and AI–NEMD simulations with the objective of computing the conductivity and recognizing the technique of diffusion in pure Li6PS5Cl, Li6PS5Cl with sulfur–chlorine disarray (sulfur and chlorine switching locations), and Li6PS5Cl with mutually lithium-ion vacancies with sulfur–chlorine disarray.
6.1. Li6PS5Cl Pure Diffusion
Six Li-ions move in an octahedral region around an S2 S atom in one of the two different motion types, while a second Li-ion transposes in the center of these octahedral borders in the other. If the skips time is more than the time of simulation, then no conclusion is viable on the diffusion coefficient from the simulation. For AI–EMD simulations of Li6PS5Cl, they did not notice jumps between cages in ten independent trajectories of 100ps at 300 K and 450 K and extraordinarily little, or no jumps were visible for the 600 K trajectories. This proposes a small coefficient of diffusion of the material at 300 K (not up to 10−4 S.cm−1) and exemplifies the strain of assessing the result of the conductivity by EMD computations [64]. However, it is a simple exercise to obtain conductivity results utilizing NEMD computations at 600 K and 800 K, where jumps observation is available, and to gauge the conductivity at 300 K using an extrapolation of these results. Baktash et al. [19] envisaged the pure Li6PS5Cl conductivity ranging from 10−5–10−4 S.cm−1. The period of simulation needed to obtain a corresponding accuracy for the Li6PS5Cl conductivity through the EMD method at 600 K and 800 K was restraining as mean and standard error jumps did not take place. Meanwhile, considering another option at elevated temperatures, the extrapolated errors will be much more if the lowest temperature tends to be greater, eventually leading to a disordering of the complex followed by a diffusion coefficient with a corresponding non-Arrhenius behavior. Thus, the NEMD method is a more suitable option.
The pure Li6PS5Cl lithium-ion conductivity was formerly established empirically [20,32,65] and computationally [17,21] at 300 K. It is interesting to note that the calculations from earlier publications for pure Li6PS5Cl at 300 K differ by five orders of magnitude and are between one and four orders of magnitude distinct from the actual data [19]. They obtained a lower extrapolated data for simulations at 600 K and above. Consequently, reports show no existence of consistent computational approximates of the diffusion coefficient for this system. Under this condition, neither jump frequency of lithium-ions in Li6PS5Cl in ambient condition at about 109 s−1 [7] demands extrapolation of the elevated temperature and use of AI–NEMD to predict the conductivity at lower temperatures.
6.2. Li6PS5Cl: Disorder Effect
The Li6PS5Cl high conductivity spotted in several research studies is as a result of the disarray of Cl and S atoms [7,20,66]. To apprehend this, the consideration of a model with disarray based on the empirically scrutinized structure is important. There is a swapping of 25 percent of the Cl ions holding Li6PS5Cl 4a areas/sites with S2 ions which occupied 4c areas/sites. EMD simulations values were taken to determine the conductivity of the disarrayed configuration at 600 K and 800 K. Assuming Arrhenius behavior, the empirical values for the conductivity of the disarrayed configuration are relayed in Baktash et al. [19] as squares and triangles [7,31,67,68] with reported computational results [21]. Studying the error bars, the computed result for the conductivity of the dissembled structure, aligns with the contemporary empirical results reported by Yu et al. [7]. As a result, the disorganized structure has a conductivity that is two orders of magnitude greater than the pure Li6PS5Cl structure. Accordingly, minor structure changes include replacing four out of the 104 atoms, gives a sizeable altering of the conductivity. This demonstrates that minute voids in the pure Li6PS5Cl crystal might result in a range of empirical conductivities. There is the regulation of the diffusion mechanisms of the ordered and disarrayed Li-ions structures at 600 K using AI–EMD simulations (Figure 5). Comparing the methods, it is evident that switching the positioning of Cl and S ions cause a disarray that alters the freedom of the Li-ions. Figure 5a,b show the movement of pure Li-ions in the octahedral regions produced by the (Figure 1), and the paths through the regions show that the energy barrier for diffusion out of the regions is high when compared to the available thermal energy, which is why the pure crystal ionic conductivity is hardly discernible from these AI-EMD simulations.
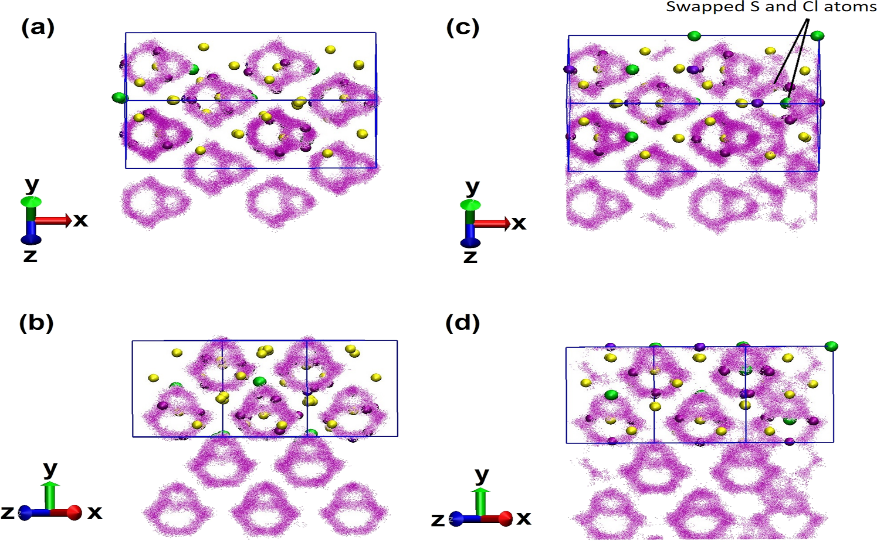
Figure 5. Li ion trajectories views, pure Li6PS5Cl (a,b) and (c,d) for S-Cl disarrayed Li6PS5Cl at 600 K observed up to 50ps. Li (violet), S (yellow), Cl (green) and P (light purple). The diffusion pathways of Li-ions = small violet dots. The apertures illustrate simulation supercell. Adapted from Baktash et al. [19].
While in the disordered structure, an aperture linking the cages is visible, Figure 5c,d. This demonstrated that in the new passage direction, diffusion of lithium-ion barrier energy is miniature compared with other regions and with the size it used to be in the pure structure, as lithium-ions advance into the dissembled area more readily.
6.3. Li6PS5Cl: Li-ions Vacancies and S–Cl Disorder
Yu et al. [66] proposed the empirically formed specimen to possess an empirical formula of Li5.6PS4.8Cl1.2 after heat treatment. They believed that the charges were not balanced in the empirical formula presented; however, a formula that comes near to charge balance is Li5.8PS4.8Cl1.2. Considering the influence of the fusion of a lithium vacancy, and a few more chlorine ions and fewer S2 ions [67] on the Li6PS5Cl ionic conductivity, two Li-ions were removed from the Li6PS5Cl supercell (8–unit cells) and two S2 ions were changed with two chlorine ions [45], delivering a novel Li5.75PS4.75Cl1.25 structure, more like the formula reported in previous work (Li5.8PS4.8Cl1.2). The calculated conductivity of the ions in this structure at 300 K was 0.09 ± 0.03 S.cm−1, which is somewhat higher than the calculated result for Li6PS5Cl with disorder of the sulfur and chlorine atoms alone (6 × 10−3–10−1 S.cm−1) and higher than the evaluated value for pure Li6PS5Cl solid electrolyte. The approximated result for the ionic conductivity is also greater than that related as 1.1 × 10−3 S.cm−1 in Yu et al. [66]. However, sensitivity to voids and disarray means they are not anticipated to match, as a result of the variance in empirical formulas. It is obvious that the diffusion of the structure is improved by lithium vacancies and the substitution of a sulfur ion for a chlorine ion. They were prepared for this increase since the lithium vacancies and the small masses of the chlorine and sulfur ions tend to cause the mobility of the lithium-ions in space, and the disorder caused by the substitution of chlorine ions for sulfur ions may facilitate easy movement.
Table 4 shows a compendium of conductivities of the various type Li6PS5Cl structures (pure, disarrayed, and structures with both disarray and lithium vacancies) reported from computational works. From the outcomes of the computations and previous reviews [17,20,21,27,30,32,66], pure Li6PS5Cl has a quite low conductivity of 10−5–10−4 S.cm−1. However, impurities such as lithium vacancies, ion disorder, and grain boundaries instituted during the synthesis of argyrodite electrolyte would affect their final conductivity.
Table 4. The conductivity of Li6PS5Cl and defective materials at 300 K investigated in tens of research and computational studies.
|
Material |
IC (S.cm−1) |
Reference |
|
Li6PS5Cl |
1.4 × 10−5 |
Experiment [32] |
|
3.3 × 10−5 |
Experiment [20] |
|
|
6 × 10−5–3 × 10−4 *a |
AI–NEMD [19] |
|
|
6 × 10−5 |
Experiment [65] |
|
|
0.29 |
Computation (MSD) [21] |
|
|
0.05 (0.16) |
Computation (Jump) [21] |
|
|
2 × 10−6 |
Computation (MSD) [17] |
|
|
Li5.6PS4.8Cl1.2 |
1.1 × 10−3 |
Experiment [66] |
|
Li5.75PS4.75Cl1.25 |
6 × 10−2–1.2 × 10−1 *a |
[19] |
|
Li6PS5Cl with chlorine and sulfur disorder |
1.9 × 10−3 |
Experiment [67] |
|
4.96 × 10−3 |
Experiment [7] |
|
|
3.38 × 10−3 |
Experiment [68] |
|
|
0.26 |
Computation (MSD) [21] |
|
|
0.89 (1.29) |
Computation (Jump) 21] |
|
|
6 × 10−3–0.1 *a |
AI–EMD [19] |
*a—extrapolation ranges at 800 K and 600 K. Adapted from Baktash et al. [19].
7. Methods of Argyrodite Electrolyte Modeling
Previous works have reported that MD simulations were used to examine the characteristics of ionic liquid (IL) electrolytes close to cathodic electrodes [69]. It is pertinent that we describe that the interfacial structure of IL electrolytes was first considered with MD simulation, as reported by Lynden-Bell [70] and Lynden-Bell et al. [71]. Some novel advancement on the theory of electric double layer, and computer simulation of interfacial structures of IL., new coarse-grained ILs and foregoing discoveries on MD are outlined by Fedorov et al. [72]. With respect to other work conducted, we decided to streamline our reviews on the modeling of ab initio MD simulation in the ensuing section.
7.1. Ab Initio MD Simulations
Ab initio Born–Oppenheimer MD simulation was carried out by the CP2K (Quickstep package) [73,74] with an improved version of the same that utilized the AI-NEMD procedure. Other research work in the literature inculcated the Vienna Ab initio Simulation Package (VASP) [3] for this same simulation [1,17,75]. Researchers preferred the PBE generalized gradient approximation (GGA) for the density functional theory [3,14] exchange-correlation functional. Van der Waals interactions reported the corrections of the DFT-D3 [76], an approach for many works in the literature. The pseudopotentials of Goedecker, Teter and Hutter (GTH–POTENTIAL) were used [77]. They usually select the DZVP–MOLOPT–SR–GTH [78] basis set as an optimization tool for molecular gas properties and condensed-phase computations. Researchers used the Gaussian and plane-waves (GPW) basis [79] and a cutoff energy (in Rydberg) to further the task. Researchers used a 1 × 1 × 1 k-point mesh (Γ point) in all computations, and initial optimization computations showed the use of grid-initiated errors not up to 0.01 Å for lattice parameters and errors not up to 0.06 eV for the energy per unit cell. The optimized lattice constants, 10.08 Å, used are 2.5% more than the empirically described results for Li6PS5Cl and compared with previous computational reports [17,21].
7.2. Equilibrium and Nonequilibrium Models of Motion
EMD and NEMD simulations assess the coefficients of the diffusion of materials in the NVT ensemble (constant-temperature, constant-volume). The models of motion for the AI–EMD simulations are [61,80]:
|
(3) Please see equation in the published paper |
|
|
(4) Please see equation in the published paper |
where = position, = momentum, = mass of atom , = inter-atomic force on atom , α = Nosé–Hoover thermostat couples of the atoms. A chain thermostat with the chain number of 3 (typical for CP2K) for EMD computations was employed [19,61,81]:
|
(5) Please see equation in the published paper |
|
|
(6) Please see equation in the published paper |
|
|
(7) Please see equation in the published paper |
In the above equations, Q1, Q2, and Q3 = coefficients of friction, all given the same inputs of three in the equilibrium simulations, kB = Boltzmann’s constant, T = target temperature and g = degrees of the system freedom. The non-equilibrium approach applied to resolve the coefficient of diffusion for lithium ion is the color-diffusion algorithm that is broadly functional in classical MD simulations [80–82]. The equations of motion for ions utilizing this line of instruction are given in Equations (3) and (4); however, the equation of motion for the momentum of the lithium-ions is given. Equation (4) was modified to incorporate a force brought on by a color field, Fc. [80]:
|
(8) Please see equation in the published paper |
where ci = color charge of lithium ions. The summation of the color charge = 0, ensuring that no drift of moment occurs in the system, but the selection of these charges is random. There is always +1 color label on half of the lithium-ions and −1 color charge on the other half. , S2− and Cl− are not directly affected by the color field, and the color charges do not affect how the Li+ interact with one another; rather, the color field simply affects the field response. Because a chain thermostat is inappropriate for non-equilibrium simulations, it was not applicable for NEMD computing [83].
Using the velocity Verlet technique in the 1fs time step, it is crucial to extend the EMD and NEMD equations of motion. Using the Nernst–Einstein equation and the coefficients of self-diffusion, researchers may determine the ionic conductivity of any specimen, σ [17,21,80]:
|
(9) Please see equation in the published paper |
where n is the ion density of Li, e is the elementary electron charge, and Z the valence of Li.
Using the NEMD simulations, the self-diffusion coefficient is derived from the computation of the color current by the color field. Remarkably, this approach determines the self-diffusion coefficient of an SSE with minimal conductivity. The color current is [18]:
|
(10) Please see equation in the published paper |
where = velocity of th lithium ion. At low fields, the color current in the direction of the field (= varies directly to the field, , when the systems are in a steady state, and then for the color charges reported in Evans et al. [61]:
|
(11) Please see equation in the published paper |
where N = number of Li-ions subject to a color field. Using a disparate choice of color charges, we substitute N in Equation (11) with . The system and condition, including temperature, will have an impact on the field’s outcome if there is a linear change between the color current and applied field. Baktash et al. [19] conducted simulation in practice to calculate the critical field. So, to obtain values with the least statistical error, maximum field for which linear response occurs is better utilized. In ergodic order, researchers substituted the color current ensemble average in Equation (11) with a time average, using [19]:
|
= |
(12) Please see equation in the published paper |
In the horizontal direction, the self-diffusion coefficient is [77,79]:
|
(13) Please see equation in the published paper |
The field accumulates force to the molecules in the orientation of the field assuming a corresponding influence to diminishing the activation energy bar for diffusion [84].
The predicted time for a specific leap, if the diffusion method is synthesized as a jump process, will increase with the size of the activation bar. As a result, using the field discharge permits systems with lower diffusion coefficients for a given simulation duration. This proves that there is a great edge for NEMD computations for systems with minimal coefficients of diffusion. Since the ionic conductivity of SSEs depends on temperature, researchers used ionic conductivities at elevated temperatures calculated from MD simulations to specify the coefficients of diffusion of the electrolytes at reduced temperatures, considering the Arrhenius equation [1,17]:
|
(14) Please see equation in the published paper |
where = activation energy, and = diffusion pre-exponential factor. Using Equation (9), we express this in terms of the ionic conductivity of the process [19,85],
|
(15) Please see equation in the published paper |
Note that for systems where only the Li-ions are moving and transpose separately, the conductivity computed from the Einstein equation for the self-diffusion, Equation (1), which is written as a Green–Kubo equation, [80–82].
|
= |
(16) Please see equation in the published paper |
Furthermore, if the theory of independency of motion of the Li-ions is open, then computed from the coefficient of collective diffusion and the Green–Kubo relationship as [81–82],
|
|
(17) Please see equation in the published paper |
The Einstein expression used in Zhou et al. [8] avoids problems correlated with convergence of the time-correlation functions in Equations (16) and (17). Importantly, ab initio MD simulations of conductivity has been reported in the literature, and it has been emphasized that that Green–Kubo equation provides regular results using integer charges and velocities of distinct sites, as shown in Baktash et al. [19], and the mean-square dipole displacement computed using Born charges of each atom [86].
7.3. Machine Learning (ML) Models
The machine learning models provide an approach to juxtapose the atoms in a large molecule and their neighboring counterpart, giving a representation of their bonding and interaction. Again, ML makes it easy to make projections for the energies of large molecules or the disparities between the low-accuracy and high-accuracy computations. It is pertinent to add that ML is appropriate to the search for stable and harmless electrolytes for LIBs [87]. Additionally, ML provides solutions to mitigate orders of magnitude in calculations and big data analysis [88]. A lot of models and equations on ML were extensively reported in Refs. [88,89] to calculate DFT using VASP for the total energies and electron densities.
Partial density states that computations for LiPS4 and LiPO4 can be computed with the form [85]:
|
(18) Please see equation in the published paper |
The smearing factor () is always chosen to be 0.1 eV. is the Brillioun zone sampling factor. is the weighing factor, n is the band index, and k is the wave vector.
8. Discussion
We reviewed the investigation of the diffusion technique of lithium-ions in Li6PS5Cl and Li5PS4Cl2 and their coefficients of diffusion. They used the assessment of the EMD and NEMD methods to estimate the ionic diffusion of these materials, whilst their ionic conductivity is about 10−3–10−2 S.cm−1. At any time when the ionic conductivity of these samples is low, the EMD simulation time required for short and simple results is currently infeasible. However, it was shown that it is viable to use NEMD to calculate coefficients of diffusion of SSEs with conductivities in the range 10−6–10−4 S.cm−1. The consensus on the results of these techniques has shown that if conductivity is increased sufficiently, both can provide reliable measurements of conductivity. However, for low-conductivity resistance SSEs that are close to ambient temperature, NEMD simulation should be used.
As the diffusivity decreases, the advantage of NEMD calculations over EMD calculations grows. This is due to the fact that the diffusion coefficient has an inverse relationship with the amount of time needed to explore a material in equilibrium simulations [65], but the applied force field also affects the NEMD simulation. It is important to perform different NEMD simulations on fields in distinctive directions to calculate the diffusivity, especially if the diffusion is not isotropic. Therefore, in this case, the NEMD efficiency calculation is minimized. However, it is necessary even if the field is small enough.
We additionally reviewed the conductivity of Li5PS4Cl2 and Li6PS5Cl from past and recent works, and also the effect of disarray and defects on diffusion of the Li-ions in Li6PS5Cl. Predictions made proved that Li5PS4Cl2 is a highly conductive solid electrolyte while its synthesis is in progress. For Li6PS5Cl, though the pure material has a moderately low ionic conductivity and was found to be metastable [38,43] (6 × 10−5–3 × 10−4 S.cm−1 at 300 K), it is proven that by intensifying lithium vacancies of the structure and establishing disarray in the ionic positioning of the chlorine and sulfur ions, the ionic conductivity of the material can be improved. Whilst they pronounced those structures formerly, the dimensions of the error bars made it tough to envision the effects. In summary, the experimentally reported increase in conductivity of Li6PS5Cl is assumed to be as a result of a combination of lithium-ion vacancies with chlorine–sulfur ion damage, or an increase in halogen (Cl) concentration after heat treatments. The computational results mentioned in a paper by Baktash et al. predict conductivities that are either greater than the actual values or at the upper end of the range of empirical values [19]. The modeling of the system size, the degree of theory employed in the ab initio MD simulations, and changes in the lattice parameters during diffusion carried out under constant volume circumstances are a few systematic flaws in the calculations that might potentially lead to this. Nonetheless, the existence of grain boundaries, contaminants, chaotic, and non-uniform distribution of chaotic sites in the experimental sample may explain the discrepancy between the actual and calculated results. It is important that the calculated results are duplicatable and show trends due to structural changes indicating ways to tune a material to increase conductivity, which is essential for improving SSE.
Based on findings reported by Zhao et al. [89] about some promising compositions, which can be further verified experimentally, it should be noted that some substitutions may be challenging due to the limited solid solution ranges and may require special synthesis conditions [90]. Simultaneously, the solubility itself can be included in the ML predictive model. This will be the focus of future research work.
From reports from the literature, the creation of mechanical stress during discharge in a dual porous insertion electrode cell sandwich made of lithium cobalt oxide and carbon is simulated using models that are given [91]. Models credit two separate factors—changes in the lattice volume brought on by intercalation and phase transformation during the charge or discharge process—to the stress accumulation within intercalation electrodes. Models are used to forecast how cell design elements such as electrode thickness, porosity, and particle size will affect how much stress is generated. To comprehend the mechanical deterioration in a porous electrode during an intercalation or de-intercalation process, models described in the literature are employed. The usage of these models leads to an improved design for battery electrodes that are mechanically durable over an extended time of operation. Refs. [92–103] are recommended to readers for these models.
9. Conclusions
The lithium conductivity in argyrodite electrolytes makes ASSB transcend to be a preferable option for clean electrical energy storage. Scholars have considered a scalable solution-synthetic approach to model argyrodite phases using solvate complexes to enhance elevated ionic conductivities of about 3.9 mS·cm−1 with minimal electronic conductivities. ASSB showed great stability performance and good agreement between cells formed by ball-milling and solution-engineered approaches.
Researchers have shown that the AI-NEMD simulation provides a good approximation of the coefficient of diffusivity found in materials with diffusivity that are not intended to be determined directly by the AI-EMD computations. They calculated diffusion coefficients using AI–NEMD and AI–EMD simulations for highly diffusive SSE obtaining accuracy. It was proven from the literature that the AI–EMD approach tends to be slow when used to compute the diffusion coefficients, whereas it is better when using AI–NEMD simulations.
Using AI–NEMD simulations, Li6PS5Cl and Li5PS4Cl2 were separated as two potential electrolytes for ASSB. It was demonstrated that by including Li vacancies and disorder into the argyrodite electrolyte system, the ionic conductivity of that material will improve substantially.
We reviewed sulfide-based electrolytes reported in the literature as a few potential materials of ASSB because of their mechanical qualities, ionic conductivities, and electrochemical stability surpassing many other potential SSE. We reported that it is possible to construct structures that are stable in the higher conductivity phase at room temperature by introducing halogens into argyrodite models, such as Li7PS6.
It was proven that ionic conductivity is good for heterogeneous Cl and Br phase and Cl-rich phases, yielding about 4 mS·cm−1. This shows that the dopants impurities effects of the synthesized argyrodites electrolyte materials does not reduce Li-ions conductivity in the exceptionally fine electrolytes.
Certainly, so far, cells in the literature have been reported to utilize lithium alloy as an anodic electrode due to its toughness, with the goal of measuring the qualities of argyrodite. Future research is expected to make use of lithium as a discrete cathodic substance to see its reaction.
Additionally, future work is expected to factor the ML predictive model extensively into the synthesis of argyrodite electrolyte materials.
Overall, we plan to make this article an all-in-one resource for researchers to access information on the previous and current work on the modeling of argyrodite electrolyte materials with their related references. We included models and methods used by researchers to model the argyrodite electrolyte materials they considered. We also introduced other resources to access more models of argyrodite using ML.
Author Contributions: Conceptualization, S.F., A.P., O.M.A and S.A.O.; Supervision, S.F. and A.P.; Writing—original draft, O.M.A.; Writing—review & editing, S.F., A.P., S.A.O. All authors have read and agreed to the published version of the manuscript.
Funding: This research received no external funding.
Informed Consent Statement: Not applicable.
Acknowledgement: The support of the University of Akron is highly appreciated.
Conflicts of Interest: The authors declare no conflict of interest.
Nomenclature
|
Symbol |
Description |
| Please view missing notation in the published work |
activation energy |
|
n |
band index |
|
kB |
Boltzmann’s constant |
| Please view missing notation in the published work |
Brillioun zone sampling factor |
| Please view missing notation in the published work |
Lithium center-of-mass coefficient of diffusion |
|
ci |
color charge/label |
| Please view missing notation in the published work |
color current |
|
Fc |
color field |
|
α |
Nosé–Hoover thermostat couples of atoms |
| Please view missing notation in the published work |
diffusion pre-exponential factor |
| Please view missing notation in the published work |
ith displacement of N lithium-ions over a period |
|
e |
elementary electron charge |
| Please view missing notation in the published work |
ensemble average |
|
Q1, Q2 and Q3 |
friction coefficients |
|
Please view missing notation in the published work |
inter-atomic force on atom |
|
n |
ion density of Li |
|
σ |
ionic conductivity of the material |
| Please view missing notation in the published work |
mass of atom |
| Please view missing notation in the published work |
momentum |
|
g |
number of degrees of freedom |
|
N |
number of lithium-ions subject to a color field |
| Please view missing notation in the published work |
partial densities states |
| Please view missing notation in the published work |
position |
| Please view missing notation in the published work |
ith position of lithium-ion at time t |
| Please view missing notation in the published work |
coefficient of self-diffusion |
| Please view missing notation in the published work |
smearing factor |
|
T |
target temperature |
|
Z |
valence of Li |
| Please view missing notation in the published work |
velocity of th Li-ion |
|
k |
wave vector |
| Please view missing notation in the published work |
weighing factor |
|
Å |
Angstrom |
|
AI–EMD/EMD |
Ab initio equilibrium molecular dynamics |
|
AI–NEMD/NEMD |
Ab initio nonequilibrium molecular dynamics |
|
ASSB |
All-solid-state batteries |
|
ASSLB |
All-solid-state lithium battery |
|
DC |
Direct current |
|
DFT |
Density functional theory |
|
DME |
Dimethoxy ethane |
|
EC |
Electronic conductivity |
|
EIS |
Electrochemical impedance spectroscopy |
|
GGA |
Generalized gradient approximation |
|
GPW |
Gaussian and plane-wave |
|
IC |
Ionic conductivity |
|
IL |
Ionic liquid |
|
LIB |
Lithium-ion batteries |
|
MD |
Molecular dynamics |
|
ML |
Machine learning |
|
MSD |
Mean square displacement |
|
PBE |
Perdew–Burke–Ernzerhof |
|
Ry |
Rydberg |
|
SEM |
Scanning electron microscope |
|
SS |
Stainless steel |
|
SSB |
Solid-state batteries |
|
SSE |
Solid-state electrolyte |
|
THF |
Tetrahydrofuran |
|
VASP |
Vienna Ab initio Simulation Package |
|
XRD |
X-ray diffraction |
References
- Oluwasegun M. Ayoola; Alper Buldum; Siamak Farhad; Sammy A. Ojo; A Review on the Molecular Modeling of Argyrodite Electrolytes for All-Solid-State Lithium Batteries. Energies 2022, 15, 7288, 10.3390/en15197288.
 Encyclopedia
Encyclopedia