Physically-based models are the most commonly used tools in quantitative groundwater flow and solute transport analysis and management. Traditionally, the conceptual or numerical models are applied to hydrological modelling in order to understand the physical processes characterising a particular system, or to develop predictive tools for detecting proper solutions to water distribution, landscape management, surface water–groundwater interaction, or impact of new groundwater withdrawals. The need to address groundwater problems through alternative, relatively simpler modelling techniques pushed authors in different parts of the world to explore machine learning models.
- groundwater
- physically-based models
- artificial neural network
1. Physically Based Numerical Groundwater Flow Models
2. Machine Learning Models
2.1. Artificial Neural Networks (ANNs)
2.2. Radial Basis Function Network (RBF)
2.3. Adaptive Neuro-Fuzzy Inference System (ANFIS)
2.4. Time Lagged Recurrent Neural Networks (TLRNs)
2.5. Extreme Learning Machine (ELM)
2.6. Bayesian Network (BN)
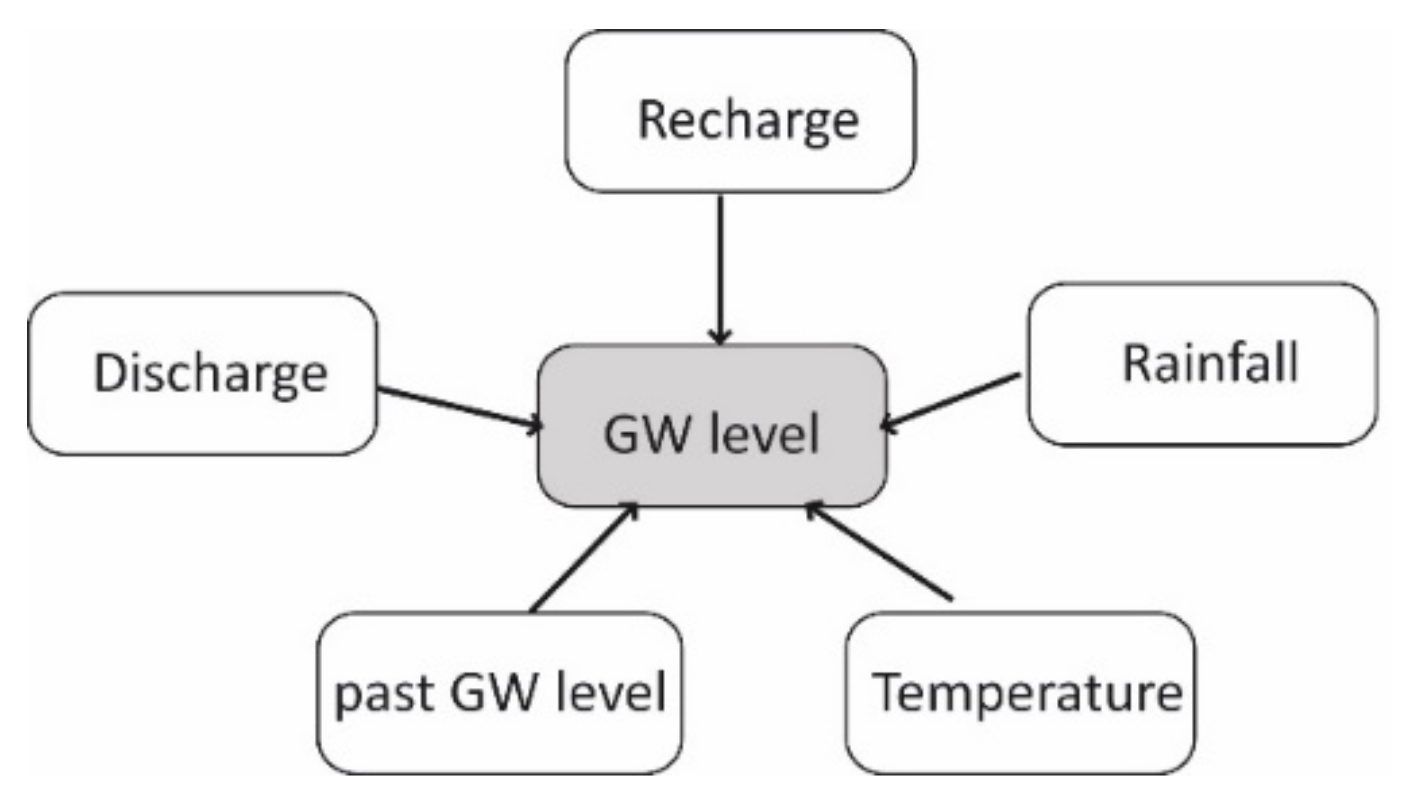
2.7. Instance-Based Weighting (IBW)
2.8. Support Vector Machine (SVM)
2.9. Decision Trees (DT)
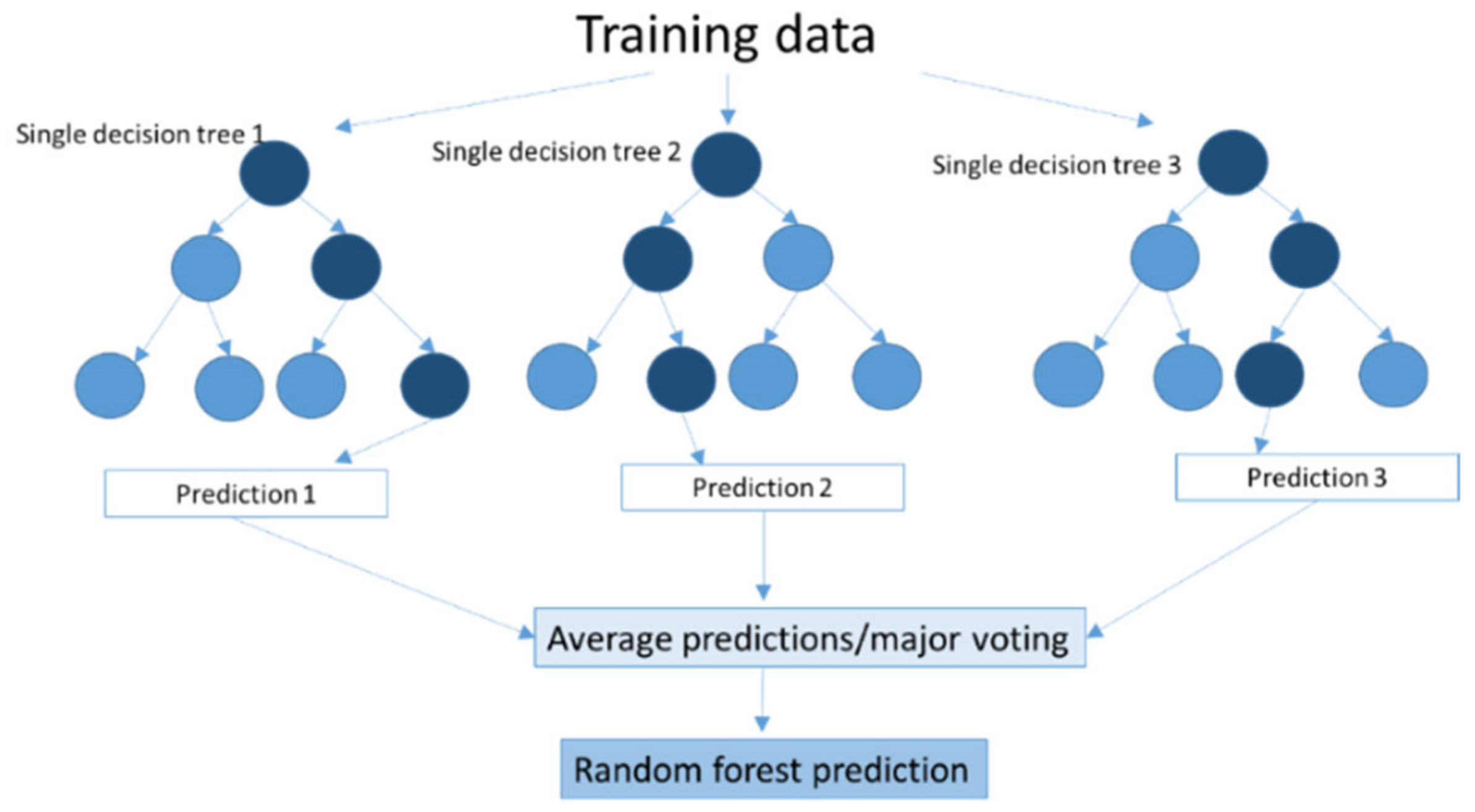
2.10. Random Forest (RF)
2.11. Gradient-Boosted Regression Trees (GBRT)
This entry is adapted from the peer-reviewed paper 10.3390/w14152307
References
- Coppola, E., Jr.; Szidarovszky, F.; Poulton, M.; Charles, E. Artificial neural network approach for predicting transient water levels in a multilayered groundwater system under variable state, pumping, and climate conditions. J. Hydrol. Eng. 2003, 8, 348–360.
- McDonald, M.G.; Harbaugh, A.W. A modular three-dimensional finite-difference ground-water flow model. In US Geological Survey Report 06-A1; US Geological Survey: Reston, VA, USA, 1988; p. 586.
- Harbaugh, A.W.; Banta, E.R.; Hill, M.C.; Mcdonald, M.G. MODFLOW-2000, the US geological survey modular ground-water model—User guide to modularization concepts and the ground-water flow process. In US Geological Survey Open-File Report 00-92; US Geological Survey: Reston, VA, USA, 2000; p. 121.
- Winston, R.B. MODFLOW-related freeware and shareware resources on the internet. Comput. Geosci. 1999, 25, 377–382.
- Voss, C.I. A Finite-Element Simulation Model for Saturated–Unsaturated, Fluid-Density-dependent Ground-Water Flow with Energy Transport or Chemically Reactive Single-species. In Water-Resources Investigations Report 84-4369; US Geological Survey: Reston, VA, USA, 1984.
- Babu, D.K.; Pinder, G.F. A finite element–finite difference alternating direction algorithm for 3- dimensional groundwater transport. Adv. Water Resour. 1984, 7, 116–119.
- Bentley, L.R.; Kieper, G.M. Verification of the Princeton Transport Code (PTC). In Engineering Hydrology, Proceedings of the Symposium Sponsored by the Hydraulics Division of the American Society of Civil Engineers, San Francisco, CA, USA, 25–30 July 1993; American Society of Civil Engineers: New York, NY, USA, 1993; pp. 1037–1042.
- Ewen, J.; Parkin, G.; O’Connell, P.E. SHETRAN: A coupled surface/subsurface modelling system for 3D water flow and sediment and solute transport in river basins. ASCE J. Hydrol. Eng. 2000, 5, 250–258.
- Hsu, K.L.; Gupta, H.V.; Sorooshian, S. Artificial neural network modeling of the rainfall-runoff process. Water Resour. Res. 1995, 31, 2517–2530.
- Schalkoff, R.J. Artificial Neural Networks; McGraw-Hill Higher Education: New York, NY, USA, 1997; p. 448.
- Mohammadi, K. Groundwater Table Estimation Using MODFLOW and Artificial Neural Networks. In Practical Hydroinformatics; Abrahart, R.J., See, L.M., Solomatine, D.P., Eds.; Water Science and Technology Library: Springer: Berlin/Heidelberg, Germany, 2009; Volume 68.
- Samarasinghe, S. Neural Networks for Applied Sciences and Engineering: From Fundamentals to Complex Pattern Recognition; Auerbach Publications: New York, NY, USA, 2016; ISBN 0429115784.
- Taormina, R.; Chau, K.-W.; Sethi, R. Artificial neural network simulation of hourly groundwater levels in a coastal aquifer system of the Venice lagoon. Eng. Appl. Artifi. Intellig. 2012, 25, 1670–1676.
- Wunsch, A.; Liesch, T.; Broda, S. Forecasting groundwater levels using nonlinear autoregressive networks with exogenous input (NARX). J. Hydrol. 2018, 567, 743–758.
- Chen, C.; He, W.; Zhou, H.; Xue, Y.; Zhu, M. A comparative study among machine learning and numerical models for simulating groundwater dynamics in the Heihe River Basin, northwestern China. Sci. Rep. 2020, 10, 1–13.
- Schwenker, F.; Kestler, H.A.; Palm, G. Three learning phases for radial-basis-function networks. Neural Netw. 2001, 14, 439–458.
- Buhmann, M.D. Radial Basis Functions: Theory and Implementations; Cambridge University Press: Cambridge, UK, 2003; p. 258.
- Kingston, G.B.; Maier, H.R.; Lambert, M.F. Calibration and validation of neural networks to ensure physically plausible hydrological modeling. J. Hydrol. 2005, 314, 158–176.
- Jang, J.S.R. ANFIS adaptive-network-based fuzzy inference systems. IEEE Trans. Syst. Man. Cybern. 1993, 23, 665–685.
- Kurtulus, B.; Razack, M. Modeling daily discharge responses of a large karstic aquifer using soft computing methods: Artificial neural network and neuro-fuzzy. J. Hydrol. 2010, 381, 101–111.
- Almuhaylan, M.R.; Ghumman, A.R.; Al-Salamah, I.S.; Ahmad, A.; Ghazaw, Y.M.; Haider, H.; Shafiquzzaman, M. Evaluating the Impacts of Pumping on Aquifer Depletion in Arid Regions Using MODFLOW, ANFIS and ANN. Water 2020, 12, 2297.
- Chen, S.H.; Lin, Y.H.; Chang, L.C.; Chang, F.J. The strategy of building a flood forecast model by neuro fuzzy network. Hydr. Proc. 2006, 20, 1525–1540.
- Haykin, S. Communication Systems, 2nd ed.; Wiley: New York, NY, USA, 1994; pp. 45–90.
- Saharia, M.; Bhattacharjya, R.K. Geomorphology-based time-lagged recurrent neural networks for runoff forecasting. KSCE J. Civ. Eng. 2012, 16, 862–869.
- Sattari, M.; Taghi, K.Y.; Pal, M. Performance evaluation of artificial neural network approaches in forecasting reservoir inflow. Appl. Math. Model. 2012, 36, 2649–2657.
- Huang, G.B.; Chen, L.; Siew, C.K. Universal approximation using incremental constructive feedforward networks with random hidden nodes. IEEE Trans. Neural Netw. 2006, 17, 879–892.
- Huang, G.B.; Chen, L. Convex incremental extreme learning machine. Neurocomputing 2007, 70, 3056–3062.
- Huang, G.B.; Chen, L. Enhanced random search based incremental extreme learning machine. Neurocomputing 2008, 71, 3460–3468.
- Moghaddam, H.K.; Moghaddam, H.K.; Rahimzadeh Kivi, Z.; Bahreinimotlagh, M.; Javad Alizadeh, M. Developing comparative mathematic models, BN and ANN for forecasting of groundwater levels. Groundw. Sustain. Dev. 2019, 9, 100237.
- Cleary, J.G.; Trigg, L.E. K*: An instance-based learner using an entropic distance measure. In Machine Learning, Proceedings of the Twelfth International Conference, San Francisco, CA, USA, 9–12 July 1995; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1995; pp. 108–114.
- Smith, E.E.; Medin, D.L. Categories and Concepts; Harvard University Press: Cambridge, MA, USA, 1981; p. 203.
- Xu, T.; Valocchi, A.J.; Choi, J.; Amir, E. Use of machine learning methods to reduce predictive error of groundwater models. Groundwater 2014, 52, 448–460.
- Aha, D.W. Feature Weighting for Lazy Learning algorithms. In Feature Extraction, Construction and Selection: A Data Mining Perspective; The American Statistical Association: Boston, MA, USA, 1998; Volume 1, p. 410.
- Aha, D.W.; Kibler, D.; Albert, M.C. Instance-Based Learning Algorithms. Mach. Learn. 1991, 6, 37–66.
- Michael, W.J.; Minsker, B.S.; Tcheng, D.; Valocchi, A.J.; Quinn, J.J. Integrating data sources to improve hydraulic head predictions: A hierarchical machine learning approach. Water Resour. Res. 2005, 41, 1–14.
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995; p. 314.
- Gunn, S.R. Support vector machines for classification and regression. In ISIS Technical Report; University of Southampton: Southampton, UK, 1998; p. 66.
- Demissie, Y.K.; Valocchi, A.J.; Minsker, B.S.; Bailey, B.A. Integrating a calibrated groundwater flow model with error-correcting data-driven models to improve predictions. J. Hydrol. 2009, 364, 257–271.
- Yoon, H.; Jun, S.-C.; Hyun, Y.; Bae, G.-O.; Lee, K.-K. A comparative study of artificial neural networks and support vector machines for predicting groundwater levels in a coastal aquifer. J. Hydrol. 2011, 396, 128–138.
- Cao, L.J.; Chua, K.S.; Chong, W.K.; Lee, H.P.; Gu, Q.M. A comparison of PCA, KPCA and ICA for dimensionality reduction in support vector machine. Neurocomputing 2003, 55, 321–336.
- Vapnik, V.N. Statistical Learning Theory; John Wiley & Sons: New York, NY, USA, 1998; p. 768.
- Smola, A.J.; Sch¨olkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222.
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106.
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Routhledge: New York, NY, USA, 1984; p. 368.
- Anderton, S.P.; White, S.M.; Alvera, B. Evaluation of spatial variability of snow water equivalent in a high mountain catchment. Hydrol. Processes 2004, 18, 435–453.
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32.
- Aertsen, W.; Kint, V.; Van Orshoven, J.; Muys, B. Evaluation of Modelling Techniques for Forest Site Productivity Prediction in Contrasting Ecoregions Using Stochastic Multicriteria Acceptability Analysis (SMAA). Environ. Model. Softw. 2011, 26, 929–937.
- Fienen, M.N.; Nolan, B.T.; Feinstein, D.T. Evaluating the sources of water to wells: Three techniques for metamodeling of a groundwater flow model. Environ. Model. Softw. 2016, 77, 95–107.
