Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is an old version of this entry, which may differ significantly from the current revision.
Geospatial artificial intelligence (GeoAI) allows the harnessing of big and high-dimensional data to better understand the hydrological processes in a particular system. Specifically, GeoAI provides new data analytic tools to the entire data processing cycle, such as sensor data fusion, hydrological modeling, data assimilation, multi-objective scenario optimization, smart decision support, evaluation of climate change impact, construction of early warning systems, and geo-visualization.
- GeoAI
- artificial intelligence
- hydrological
- hydraulic
- fluvial
- water quality
1. Introduction
Geospatial artificial intelligence (GeoAI) applications in hydrology and fluvial studies are rapidly increasing and replacing the traditional methods. A reason for rapid GeoAI adoption in hydrological sciences might be linked to the progress in collecting big hydrological datasets, using automatic sensors with internet transmission, or the internet of things (IoT). Similarly, the evolution and increase in earth observation satellites (conventional and nanosatellites), unmanned aerial vehicles (UAV), light detection and ranging (LiDAR), and other surveying technologies produce high-resolution geospatial data, allowing better landscape characterization. GeoAI greatly enhances and supports decision making in integrated water resources management (IWRM) and nexus approaches [1]. Figure 1 depicts a GeoAI application model for a smart IWRM support system.
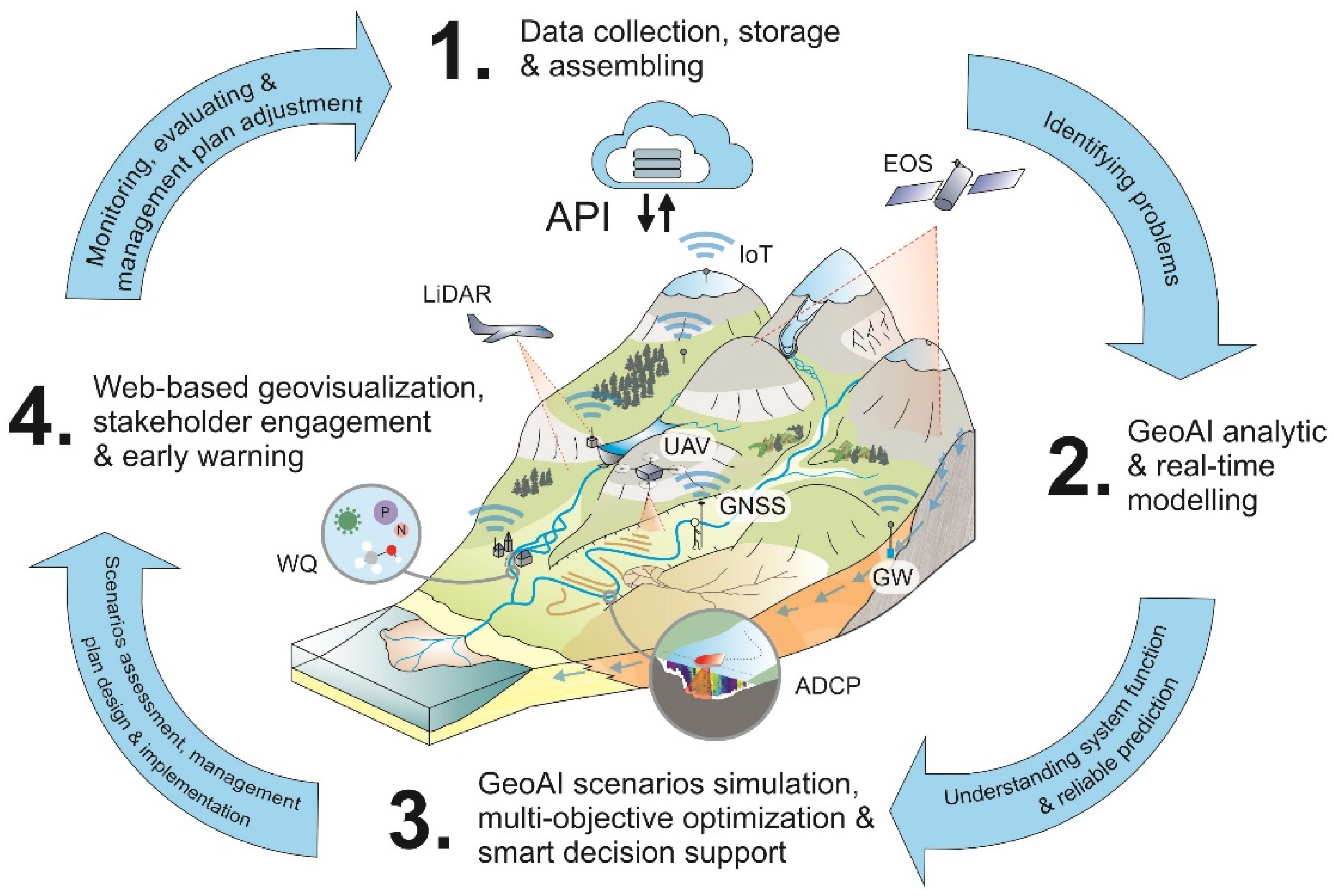
Figure 1. A GeoAI application model for a smart decision support system for integrated water resources management (IWRM). (1) Internet of things (IoT) supports real-time, high-frequency, hydrological monitoring. The data are stored in a cloud platform and accessed by an application programming interface (API). These data can be used for the real-time identification of problems in the system, e.g., a river basin. (2) GeoAI provides data analytic and online real-time modeling tools for hydrological system analysis and prediction. (3) GeoAI also supports multi-objective, multi-scenario optimization modeling, which in turn is the basis of smart decision support systems for IWRM. (4) Geovisualization in web mapping and mobile apps can be used for data dissemination and stakeholder engagements and implementing early warning systems. The smart IWRM system can be closed with the evaluation and adjustment of the IWRM plan and the improvement of the hydrological monitoring system. WQ (automatic water quality monitoring), ADCP (acoustic doppler current profiler for water current velocity measurement and river bathymetry), GW (automatic groundwater monitoring in wells), UAV (unmanned aerial vehicle for very high-resolution land cover mapping and surface elevation models), EOS (earth observation system for environmental condition monitoring), LiDAR (LiDAR survey of high-resolution topography data), and GNSS (use of global navigation satellite systems for ground truth data collection).
2. Hydrological and Hydraulic Modeling
Water flow in the catchments and river networks is a complex and stochastic process, operating in different spatio-temporal scales and characterized by non-stationarity, dynamism, and non-linearity [2][3]. These properties have limited the development of a reliable hydrological and hydraulic prediction model that can be generalized to a large geographical area. The increasing sensor-based, high-frequency (sub-hourly) hydrological data collection and the high spatial and temporal resolution mapping of land cover and topography have enhanced the understanding of hydrological processes. This fact has led to the development of more sophisticated physical-based hydrological models. However, these models are computationally expensive and limited to small-scale applications. Alternatively, several data-driven GeoAI methods have emerged for hydrological and hydraulic classification and prediction at multiple spatial-temporal scales.
2.1. Hydrological System Classification
The classification of the different types of hydrological systems is one of the most widely applied modeling tasks in hydrology and ecohydrology. It aims to find similarities between different hydrological systems, e.g., those based on the hydrological response, the hydromorphological and climatic characteristics, and other variables. Unsupervised GeoAI algorithms, such as K-mean clustering [4] and SOM [5][6], have been applied to catchment classification. Both algorithms organize multidimensional input data through linear and non-linear techniques, depending on the intrinsic similarity of the data themselves. Several studies highlight the SOM nonlinear techniques for producing robust and consistent hydrological classification [7][8][9], even though the classification consistency is highly influenced by the quality of the input variables [10]. Additionally, where training data is available, supervised GeoAI methods have produced highly accurate and biophysically meaningful catchment classification [11][12].
2.2. Hydrological Data Fusion and Geospatial Downscaling
Integrated hydrological modeling requires the extensive data collocation of different components of the hydrological system in various spatial and temporal scales. Therefore, it is necessary to complete data and/or create new data by integrating several datasets from different sources, resolutions, and measurement noisiness [13]. This approach is called data fusion. Data fusion can increase the measurement quality and reliability, estimate unmeasured states, and increase spatial and temporal coverage. Several probabilistic and GeoAI data fusion techniques are available [14][15]. The commonly used GeoAI techniques in data fusion are non-linear Bayesian regression, ANN, RF, and deep learning [14][15][16][17]. These methods provide several advantages in representing non-linear, complex, and lagged relationships in different hydrological datasets. GeoAI data fusion is also applied to automatic data denoising and anomaly detection and remote sensing data fusion [18]. GeoAI data fusion is also used in rain, soil moisture, and discharge data generation. Sist et al. [19] introduce the ANN-based data fusion of multispectral (visible and infrared) satellite data with radar (microwave) satellite data to improve rainy area mapping and the estimation of the precipitation amount. Zhuo and Han [20] used data fusion to generate soil moisture products from satellite data, land surface temperature, and multi-angle surface brightness reflectance and were able to significantly increase the availability of daily soil moisture products. Fehri et al. [21] used the best linear unbiased predictor data fusion technique to generate discharge data from crowdsourced data and existing monitoring systems. There are more examples of using data fusion in data integration in areas other than in improving knowledge, which could be the next step to be further explored.
Environmental geospatial data, particularly remote sensing data, are usually measured at different spatial and temporal scales; high-temporal resolution data are usually measured at coarse (low) spatial resolution, and fine (high) spatial resolution data are obtained with low temporal frequency [18][22]. Therefore, combining the different datasets by downscaling methods is necessary to generate spatio-temporal high-resolution data. GeoAI-based downscaling has shown several advantages. For example, CNN is frequently used for downscaling coarse-resolution to fine-resolution precipitation products, using different static and dynamic variables as predictors [23][24]. These studies have shown that CNN achieves different degrees of accuracy, depending on the precipitation rate and the condition complexity; it has, e.g., lower accuracy in extreme wet conditions [24]. Other studies have shown a higher downscaling accuracy of GeoAI methods by having a spatial component in the model, e.g., spatial RF vs. RF in downscaling daily fractional snow cover [25] and land surface temperature from MODIS data [26][27][28].
2.3. Spatial Prediction of Hydrological Variables
The application of GeoAI in hydrological spatial prediction is diverse; it can be used, for example, in the risk mapping of hydrological extremes such as flood and drought [29][30][31]. In particular, GeoAI is widely applied in flood mapping, using satellite imagery, UAVs, high resolution LiDAR topographic data, and automatic water level sensors [32][33][34]. The common GeoAI algorithms used, e.g., in flood prediction are SVM, RF, ANN, and deep learning [33][34][35]. The selection of the methods is variable and depends on the mapping objective, the system complexity, and the data availability [32]. In areas with limited data and/or complex systems, where nonlinear methods are not easily interpretable, ANFIS soft computing has been applied with good prediction accuracy and strong generalization ability [36]. ANFIS combines data and expert knowledge through a set of fuzzy semantic conditional rules [37][38][39].
Another GeoAI application is the spatial prediction of hydrological model variables, e.g., saturated hydraulic conductivity [40][41] and weather data [42]. This is particularly useful as spatial hydrological variables are not available. Thus, they can only be predicted using points observation and surrogate spatial data such as remote sensing data. GeoAI spatial prediction has shown advantages in modeling nonlinear processes. However, the prediction quality depends on the quality and quantity of the observed data points and the applied GeoAI method [43].
2.4. Hydrological Process Modeling
GeoAI has shown the potential for accurate hydrological modeling, such as for rainfall-runoff, river discharge, soil moisture dynamics, and groundwater table fluctuation [36][44][45]. The non-linear nature of these processes is challenging to model with simple empirical and physical-based models. Therefore, GeoAI methods such as ANNs have proved to be better for modeling complex hydrological processes and forecasting them in the short and long term and in different management scenarios [46]. However, traditional ANNs do not model sequential order data such as time-series data. Therefore, a further development for the temporal dynamics of hydrological sequential events is the RNN and LSTM neural networks. RNN and LSTM use the previous information in the sequence to produce the current output, although RNN is better designed to model short sequences only. In the case of long temporal sequences of the antecedent conditions, LSTM is preferred. LSTM uses an additional ‘memory cell’ compared to RNN to maintain information for long sequences or periods of time [47][48]. This memory cell lets the model learn longer-term dependencies, e.g., the effects of antecedent soil moisture conditions on runoff generation [47][49]. LSTM is advantageous for modeling hydrological processes in regions with strong seasonality, such as a northern climate with varying winter conditions [32][47]. The LTSM model also allows the use of multiple time-series predictors, such as precipitation, temperature, discharge, and time [50][51]. A further extension of LSTM is created by combining it with CNN. In CNN, learning is achieved through convolving an input with filter layers to speed up parameter optimization [49][52]. Combining CNNs and LSTM encodes both the spatial and the temporal information [28][53]. LSTM techniques can also be coupled with other signal-processing algorithms such as wavelet transformation (WT). WT is applied to time-series data decomposition, e.g., the decomposition of high- and low-frequency flow signals, the identification of seasonality and trend, the decomposition of non-stationary signals, and data denoising [54]. Denoised data are used as inputs for the LSTM model [55].
Another approach is to use a physical-based model coupled with GeoAI, e.g., for runoff and flood prediction [56][57][58]. Overall, the output of the physical-based model is used as the input for GeoAI model training. For example, Noori and Kalin [59] used the SWAT model to simulate daily streamflow and estimate baseflow and stormflow, which were used as inputs for ANNs. The benefit of this approach is that once the model is trained, it can perform orders of magnitude faster than the original physical-based models without impairing prediction accuracy [60]. Another benefit of the hybrid modeling is that a trained model, e.g., in catchment hydrological modeling, can achieve better performance for other catchments than the uncalibrated process-based models [47][57].
Overall, most of the GeoAI models achieved higher prediction accuracy than the physical-based hydrological models. However, there are several types of GeoAI algorithms, with different architectures and mathematical formulations (e.g., ANN, CNN, and LSTM) to perform similar tasks. In addition, different types of predictor variables and data sampling sizes are used, making the GeoAI model performance comparison challenging. GeoAI models are less physically interpretable, as they do not explicitly represent the physical laws governing the hydrological processes. Therefore, their causal inference is still limited. GeoAI applications are currently oriented towards hydrological prediction. GeoAI has the potential to provide accurate and timely information which is applicable to large areas, and using data from IoT sensors and cloud computing, it can deliver real-time prediction [61].
2.5. Hydraulic Modeling
The new generation of very-high-resolution river bathymetry has improved the 1D, 2D, and 3D hydraulic modeling of rivers [62][63]. River hydraulic models have been widely used in the estimation of flood extent, water depth and velocity, sediment transport, and the assessment of fluvial morphodynamics [64][65][66]. However, very complex hydraulic models (3D) are data and computationally demanding and restricted to small-scale applications. Hydraulic modeling is sometimes inconsistent and does not represent all the bio-physical processes occurring in the natural fluvial environment [67][68]. In addition, the numerical solving approach of the hydraulic model results in high numerical instability due to sensitivity to the initial and boundary conditions, model structure, and spatial and temporal discretization [69]. Thus, the GeoAI method has emerged as a promising tool for hydraulic modeling in large-scale and natural systems [56][68][70][71]. Emerging deep learning applications in computer fluid dynamics have also shown potential for the modeling of turbulent and complex flow structures [72][73][74]. Additionally, coupling the hydraulic model with the Bayesian GeoAI methods improves hydraulic modeling over a broad range of spatiotemporal scales and physical processes [75].
2.6. Hydrological Data Assimilation
Hydrological data assimilation (DA) is a state estimation theory that assumes that models are an imperfect representation of the system and that hydrological data might contain noise. Both can also contain different types of information and be complementary [76]. DA aims to harness the information in the hydrological model and in the observations to approximate the true state of the system, considering its uncertainty statistically [76][77][78]. DA methods include linear dynamics (e.g., Kalman filter, the most popular state estimation method) and nonlinear dynamics [76]. The DA methods can be related to ML. Data fusion and DA use similar techniques, but the problem formulation differs [79].
In hydrological modeling, the ML-based DA is the most common type of coupling of ML and the physical-based model, the so-called loosely hybrid hydrological model [80]. DA updates the state system predicted by a physical-based model at a given time or place with observational data, using Bayesian approximation such as the ensemble Kalman filter (EnKF) [76] or ML methods, e.g., ANN, RNN, and LSTM [81]. Both the DA and the ML methods solve an inverse problem, expressed as the model y = h(x,w), where h is the model function, x represents the state/feature variable, w is the parameters/weights of the model, and y is the observations/labels in DA/ML, respectively. DA is oriented to find the true state of the system (x) from the observation and ML is commonly oriented to find model parameters or weight (w) from the observation. DA holds w constant to estimate x; ML holds x constant to estimate w; see [82] for a detailed revision.
Many studies have shown that ANN data assimilation outperforms conventional DA, particularly for complex and non-linear response systems [83]. An additional development of ML-based DA methods is the so-called deep DA [81], which trains deep learning neural networks such as LSTM for high dynamic systems. Deep DA has shown potential for accurate prediction for periods or sites where observations are unavailable and conventional DA cannot be applied to reduce the model error [81].
3. Modeling Optimization Problems for Hydrological Model Calibration and Decision Support System
3.1. Hydrological Model Calibration
In hydrological modeling, the inverse modeling approach is widely applied. In inverse modeling, the model features and parameter values are unknown, and those are identified by minimizing the error between the model output and the observed data [84][85]. The model feature identification includes the definition of the main hydrological processes, the mathematical equations representing it, the boundary conditions, and the time regime [86]. The parameter identifications encompass the identifying of the model optimal parameter set values that reproduce the observed data acceptably [86]. In highly parameterized models, identifying the optimal values of the parameters is challenging and represents a substantial part of the modeling work. Usually, there is not a single set of optimal values of parameters that can simulate the observed data well but a set of optimal parameters values that can achieve similar model performance. This modeling phenomenon is called the non-uniqueness or equifinality problem [87]. The hydrological model calibration often requires specialized optimization algorithms, and several ML-based calibration algorithms have been developed to support model calibration.
Hydrological models are often calibrated with a single objective function, although adequate and fast multi-objective optimization techniques exist, which better support the several output variables [88]. There are many optimization algorithms, meta-heuristic and ML-based, for model parameter calibration, such as particle swarm optimization (PSO), grey wolf optimization (GWO), genetic algorithms (GAs), genetic programming (GP), strength Pareto evolutionary algorithms (SPEA), micro-genetic algorithms (micro-GA), and Pareto-archived evolution strategies (PAES). Depending on the selected performance indicators of the model, the best model for hydrologists varied. According to the free lunch theorem [89], this is not expected to change for a while; it proposes that no one model fits all. In any case, all the models performed well. See Yusoff et al. [90] and Ibrahim et al. [91] for a specific review of optimization algorithms.
Meta-heuristic optimization algorithms, which are mostly inspired by the biological/behavioral strategies of animals, provide a good solution to optimization problems, particularly with incomplete or imperfect information or limited computational capacity [92]. An advantage of these algorithms is that they make relatively few assumptions about the optimization problems and reduce the computational demand by randomly sampling a subset of solutions, which otherwise would be too large to be iterated entirely [92]. However, some meta-heuristic algorithms such as PSO may not guarantee that a globally optimal solution will be found, particularly when the number of decision variables or dimensions being optimized is large [91]. The GA is inspired by genetic evolutionary concepts, such as the non-dominated sorted genetic algorithm II (NSGA-II). The genetically adaptive multi-objective method (AMALGAM) [93] has been applied for multi-objective, multi-site calibration and to solve highly non-linear optimization problems [94][95]. AMALGAM is a multi-algorithm that blends the attributes of several optimization algorithms (NSGA-II, PSO, the adaptive metropolis search, and differential evolution) [94]. The GA has been shown to be well-suited for hydrological models, such as the SWAT semi-distributed hydrological models, which cannot be adequately calibrated by gradient-based calibration algorithms [94][95][96]. The objective function for each solution in a GA can be assessed in parallel computation, providing computational efficiency [94]. Additional calibration methods based on deep learning have also been developed, outperforming many of the existing evolutionary and regionalization methods [97][98].
3.2. Decision Support System for Integrated Water Resources Management
Integrated water resources management (IWRM) deals with multiple actors to consensually and communicatively integrate decisions in a hydrological unit to ensure equitable economic development and social welfare while assuring hydrological system sustainability [99]. IWRM demands quality and timely information. Hence, increasing automation with GeoAI-based decision support systems is thought to enhance IWRM [60][100]. Multi-objective and scenario analysis are typical applications of GeoAI techniques in IWRM to find solutions for conflicting objectives, forecast the impact of management strategies, and optimize hydrological system operation [101][102]. There are widespread applications of GeoAI in reservoir and water distribution optimization using ANN [103][104], assembled and deep learning algorithms, and genetic programming [105][106]. Another application is found in building a smart irrigation decision support system [107]. Here, partial least square regression and the adaptive network-based fuzzy inference system (ANFIS) are proposed as reasoning engines for automated decisions. An additional example of artificial intelligence application is the adaptive intelligent dynamic urban water resource planning [102]. It uses Markov’s decision process to tackle complex water management problems, predicting water demand, scheduling management, financial planning, tariff adjustment, and the optimization of water supply operations [102]. Overall, the GeoAI-based IWRM integrates various types of algorithms to perform different tasks, such as prediction and forecasting using various types of geospatial data, and optimization algorithms for management scenarios with multiple objectives. Algorithms such as ANFIS are used for system reasoning to automate the decision support [101][102][108]. ANFIS allows the mimicking of human reasoning and decision-making based on a set of fuzzy IF-THEN rules. ANFIS has the learning capability to approximate nonlinear functions and can self-improve in order to adjust the membership function parameters directly from the data [109].
4. Automatic Water Quality Monitoring and Spatio-Temporal Prediction
4.1. Automatic Water Quality Monitoring
The data collection of water quality with wireless sensor networks and internet of things (IoT) technologies is rapidly increasing and providing very-high-frequency WQ data (sub-hourly) [110][111]. There is evidence that the high-frequency data better represent the dynamics variation of river discharge and sediment and solute fluxes [112]. It enables the early mitigation of floods and drinking water problems [113][114]. High-frequency data can also lead to a more precise and accurate classification of the biochemical status of rivers and lakes [115]. However, such sensors and devices are subject to failures, poor calibration, and inaccurate data recording in certain conditions [116][117]. Therefore, automatic data quality control, error and anomaly detection, sensor drift compensation, and uncertainty assessment are important [116][117][118]. GeoAI showed advantages in managing WQ sensor networks and sensor data fusion, such as fault detection, data correction, and upgrades from different monitoring sensors by data fusion [119]. Additional applications of GeoAI are in the detection, localization, and quantification of pollutant critical sources and critical periods of loading in monitoring networks [120][121]. The most common GeoAI algorithms for WQ sensor fusion are based on Bayesian algorithms, fuzzy set theory, genetic programming, ANN, and LSTM [122][123][124][125].
Many WQ parameters cannot easily be measured in situ and in real time for various reasons, such as high-cost sensors, low sampling rate, multiple processing stages, and the requirement of frequent cleaning and calibration. Therefore, a common practice is the estimation of a particular WQ parameter value based on other surrogate parameters, called soft sensors [126][127][128]. ML techniques showed higher accuracy in implementing soft sensors than conventional regression-based models [126][127][128][129].
The ML method has also shown an advantage in automatic hysteresis pattern analysis using high-frequent water quality data with, e.g., restricted Boltzmann ANN [130]. A more detailed hysteresis pattern classification allows the gaining of new insights into WQ pollutants sources and drivers, the influence of catchment and riverine features, the effect of antecedent conditions, and the influence of changes in rainfall and snowmelt patterns [130].
4.2. Spatio-Temporal Water Quality Prediction
There are diverse applications of the GeoAI methods in WQ spatio-temporal pattern analysis, the classification of WQ, and the prediction of WQ variables and the pollutant loading estimation. A detailed review of the ML application in WQ prediction is found in Rajaee et al. [131], Naloufi et al. [132], and Chen et al. [133]. Commonly used GeoAI for WQ prediction and classification are unsupervised clustering such as k-means, density-based spatial clustering of applications with noise (DBSCAN), and SOM, but also time-series segmentation such as dynamic time warping [134]. Supervised ML classification and prediction algorithms for WQ are RF, SVM, the Bayesian network, and ANN, and deep learning such as LSTM is also frequently used [135][136][137].
High-frequency WQ monitoring data contains noise signals due to random and systematic errors, impairing the WQ prediction accuracy. Hence, combining data denoising techniques such as Fourier and wavelet transform with GeoAI improves WQ prediction. For example, Song et al. [138] found that combining synchro-squeezed wavelet transform and an LSTM network substantially improved the WQ parameter prediction. Similarly, Najah Ahmed et al. [139] integrated wavelet discrete transform with the artificial neuro-fuzzy inference system (WDT-ANFIS) to obtain high-accuracy prediction of river WQ parameters.
Additionally, the WQ data usually have temporal autocorrelation and multi-collinearity between the WQ parameters. To consider these characteristics in the prediction models, Zhou et al. (2020) [140] proposed an ML model based on t-distributed stochastic neighbor embedding (t-SNE) and self-attention bidirectional LSTM (SA-Bi-LSTM), demonstrating substantial WQ prediction improvement. Another promising approach is uniform manifold approximation and projection (UMAP) for multidimensional WQ data ordination and classification. Unlike other dimension reduction methods, UMAP retains a global and local information structure, and the data ordination is bio-physically meaningful [141].
Inland water has naturally high spatial variation. It requires complex spatial prediction models and large datasets. The GeoAI have shown breakthroughs in spatial WQ prediction by combining field observations, remote sensing data, or UAV imagery. For example, using deep learning, RF, genetic algorithm—RF, adaptive boosting (AdaBoost), genetic algorithm—AdaBoost and the genetic algorithm—extreme gradient boosting (GA-XGBoost) [127][133]. However, these models usually demand extensive training data, which are restricted to a few pilot areas or intensely monitored areas.
Another approach in WQ prediction is the application of hybrid models and the integration of physical-based models with GeoAI methods, such as SVM, RF, ANN, and LSTM. Hybrid models usually outperformed physical-based models. For example, Noori et al. [142] found substantial improvement in monthly nitrate, ammonium, and phosphate load prediction when using hybrid SWAT-ANN models. Hybrid models are also helpful for unmonitored catchment predictions [142]. The hybrid model also improves GeoAI explanatory and generalization capability, although some disadvantages observed in the physical-based model, such as extreme values not being well predicted, persisted in the hybrid models. Similarly, the process-guided recurrent neural network (RNN), which combines the biophysical principles of the process-based model and RNN, modeled the seasonal variation of lake phosphorus loading with lower bias and better reproduced the long-term changes of phosphorus loading compared to using the physical-based model and RNN independently [143].
Overall, the GeoAI water quality prediction depends not only on the selected algorithms and settings but also on the WQ parameters, data size, and training data quality for the learning models [127][142][144].
5. Machine Learning in Fluvial Geomorphic and Morphodynamic Mapping
Fluvial geomorphology triggered the quantitative dynamic paradigm [145] as an approach to quantifying and understanding the processes of the fluvial environment [64]. The simultaneous development of techniques such as multispectral satellite images, synthetic aperture radar (SAR), LiDAR, UAV imagery, structure from motion photogrammetry (SfM), multibeam sonar (sound navigation and ranging), among others, has resulted in an unprecedented, seamless characterization and quantification of the fluvial environment and its dynamics [146][147][148]. This geospatial dataset explosion, as in many other disciplines, has resulted in the perfect foundation for applying GeoAI methods in fluvial geomorphology.
The current state-of-the-art of GeoAI in fluvial geomorphology consists of an automatic extraction of fluvial features at a fine scale by integrating larger and multidimensional datasets, using unsupervised classifiers (e.g., K-means, SOM), supervised classifiers (e.g., RF, SVM, ANN, deep learning, CNN), or by combining both methods, e.g., K-means with ANN. Most of the articles were focused on the development of the methods and workflow, the testing of new applications, or the comparison of algorithm performances [149][150][151], rather than the study of fluvial processes and underlying dynamics. These applications of GeoAI provide the basis to the discovery of new fluvial patterns and trends and increase knowledge about fluvial environments (e.g., Ling et al. 2019; Guillon et al. 2020, Heasley et al. 2020) [152][153][154].
Overall, GeoAI outperforms conventional methods of fluvial landform classification, reaching a classification accuracy of over 80%. Most common applications are found in river channels and water body mapping [152][155], the classification of riverine landforms and vegetation successions [153][156][157][158], the estimation of catchment hydrogeomorphic characteristics (e.g., valley bottom, floodplain, and terrace) [159][160], and benthic and fish habitat mapping [150][161][162][163].
Another application of GeoAI is the integration of multiple techniques to provide more accurate and very-high-resolution data for fluvial studies. For example, the fluvial environment is highly dynamic and demands frequent bathymetry surveys to understand the change and morphodynamic drivers in lakes and rivers. Emerging technologies, such as acoustic Doppler current profiler (ADCP), green LiDAR, high-resolution image radiometric model, and 3D cloud points generation with SfM, allow more frequent and accurate bathymetry mapping [147][148]. However, each approach has limitations, e.g., ADCP collects data only from areas where the sensor has passed, and it does not provide continuous spatial scanning. It does not measure near-bank areas, and it is subject to the acoustic side-lobe effect [164]. Photogrammetry and the green LiDAR method are sensitive to water turbidity and light penetration in the water column [165][166]. Therefore, multisource bathymetry modeling using the GeoAI method increases the bathymetric data accuracy and reduces uncertainties due to data quality in change detection. For example, ADCP data, image radiometric-based water depth, and SfM depth data can be integrated using U-Net convolutional neural networks [167][168].
The GeoAI approach, when using multi-temporal remote sensing data, allows the mapping of a broader fluvial landscape and its change, thereby revealing spatiotemporal scales of fluvial morphodynamics, as in e.g., Van Iersel et al. [169], Hemmelder et al. [170], and Boothroyd et al. [171]. There are different GeoAI approaches for automatic change detection using multi-temporal images such as generative adversarial networks (GAN), autoencoder, CNN, and others, as presented by Shi et al. [172].
Although GeoAI has been rapidly adopted in fluvial geomorphological studies, a wide spectrum of workflows and software is found; many GeoAI approaches seem to be under development and in the testing stage. Therefore, without a general, consistent, and robust workflow among them, it is difficult to generalize and compare the GeoAI methods performance and overall accuracies, as well as the study results.
The current limitations of GeoAI methods in fluvial studies are that the classification quality is highly dependent on expert knowledge. The unsupervised classification output is often inconsistent, and the cluster classes do not have direct geomorphic or fluvial process meaning and need a post-classification labeling. Supervised GeoAI classifiers require a large training sampling, and the training data quality is highly dependent on expert knowledge. In addition, many of the studies using GeoAI to classify fluvial landform or river typologies have been conducted in areas where an extensive quantity of previous studies and data collection exists [153][159]. Therefore, its application in poorly sampled areas is somewhat limited.
In many cases, GeoAI is enhanced with the use of fine-scale fluvial geomorphic mapping, e.g., LiDAR or UAV-based images, which are still restricted to pilot areas, mostly in Western countries. In addition, several different landform class names are used to rename fine-scale fluvial landforms, and therefore, a standardized fluvial landform taxonomy is lacking [173].
Another limitation of supervised GeoAI applications is the misclassification of elements out of the GeoAI training range, as presented, e.g., in Carbonneau et al. [149]. Moreover, the use of very different methods for assessing the GeoAI algorithm’s performance and accuracy may lead to inconsistencies in the validity of results, e.g., map cross-tabulation often uses limited validation points rather than areal-based reference data, due to the lack of geomorphological reference maps at a very fine scale. Another issue with regard to performance and accuracy assessments is the use of scalar error statistics, such as root mean square error, which may not be reliable in fluvial mapping. Here the resulting error is a complex combination of random and systematic components, and the isotropy and stationary assumptions do not apply to the fluvial process [174]. It is also heavily influenced by a small percentage of classification errors, which lead to incorrect rankings of overall model performances or to prediction error [175]. Therefore, a more consistent and comparable GeoAI-based fluvial mapping accuracy assessment is needed.
This entry is adapted from the peer-reviewed paper 10.3390/w14142211
References
- Lange, H.; Sippel, S. Machine Learning Applications in Hydrology. In Forest-Water Interactions; Levia, D.F., Carlyle-Moses, D.E., Iida, S., Michalzik, B., Nanko, K., Tischer, A., Eds.; Ecological Studies; Springer International Publishing: Cham, Switzerland, 2020; pp. 233–257. ISBN 978-3-030-26086-6.
- Troch, P.A.; Carrillo, G.A.; Heidbüchel, I.; Rajagopal, S.; Switanek, M.; Volkmann, T.H.M.; Yaeger, M. Dealing with Landscape Heterogeneity in Watershed Hydrology: A Review of Recent Progress toward New Hydrological Theory. Geogr. Compass 2009, 3, 375–392.
- Sivakumar, B. Nonlinear Dynamics and Chaos in Hydrologic Systems: Latest Developments and a Look Forward. Stoch. Environ. Res. Risk Assess. 2009, 23, 1027–1036.
- Aytaç, E. Unsupervised Learning Approach in Defining the Similarity of Catchments: Hydrological Response Unit Based k-Means Clustering, a Demonstration on Western Black Sea Region of Turkey. Int. Soil Water Conserv. Res. 2020, 8, 321–331.
- Ley, R.; Casper, M.C.; Hellebrand, H.; Merz, R. Catchment Classification by Runoff Behaviour with Self-Organizing Maps (SOM). Hydrol. Earth Syst. Sci. 2011, 15, 2947–2962.
- Ley, R.; Hellebrand, H.; Casper, M.C.; Fenicia, F. Is Catchment Classification Possible by Means of Multiple Model Structures? A Case Study Based on 99 Catchments in Germany. Hydrology 2016, 3, 22.
- Swain, J.B.; Sahoo, M.M.; Patra, K.C. Homogeneous Region Determination Using Linear and Nonlinear Techniques. Phys. Geogr. 2016, 37, 361–384.
- Chen, I.-T.; Chang, L.-C.; Chang, F.-J. Exploring the Spatio-Temporal Interrelation between Groundwater and Surface Water by Using the Self-Organizing Maps. J. Hydrol. 2018, 556, 131–142.
- Chang, L.-C.; Chang, F.-J.; Yang, S.-N.; Tsai, F.-H.; Chang, T.-H.; Herricks, E.E. Self-Organizing Maps of Typhoon Tracks Allow for Flood Forecasts up to Two Days in Advance. Nat. Commun. 2020, 11, 1983.
- Prinzio, M.; Castellarin, A.; Toth, E. Data-Driven Catchment Classification: Combining Linear and Non-Linear Approaches to Improve Hydrological Predictions in Ungauged Catchments. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 22–27 April 2012; p. 11717.
- Brown, S.C.; Lester, R.E.; Versace, V.L.; Fawcett, J.; Laurenson, L. Hydrologic Landscape Regionalisation Using Deductive Classification and Random Forests. PLoS ONE 2014, 9, e112856.
- Li, Y.; Hu, T.; Zheng, G.; Shen, L.; Fan, J.; Zhang, D. An Improved Simplified Urban Storm Inundation Model Based on Urban Terrain and Catchment Modification. Water 2019, 11, 2335.
- Ebtehaj, A.M.; Foufoula-Georgiou, E. On Variational Downscaling, Fusion, and Assimilation of Hydrometeorological States: A Unified Framework via Regularization. Water Resour. Res. 2013, 49, 5944–5963.
- See, L. Data Fusion Methods for Integrating Data-Driven Hydrological Models. In Quantitative Information Fusion for Hydrological Sciences; Cai, X., Yeh, T.-C.J., Eds.; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–18. ISBN 978-3-540-75384-1.
- Meng, T.; Jing, X.; Yan, Z.; Pedrycz, W. A Survey on Machine Learning for Data Fusion. Inf. Fusion 2020, 57, 115–129.
- Qian, S.S.; Reckhow, K.H.; Zhai, J.; McMahon, G. Nonlinear Regression Modeling of Nutrient Loads in Streams: A Bayesian Approach. Water Resour. Res. 2005, 41, 1–10.
- Rawat, S.; Rawat, S. Multi-Sensor Data Fusion by a Hybrid Methodology—A Comparative Study. Comput. Ind. 2016, 75, 27–34.
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; et al. Deep Learning in Environmental Remote Sensing: Achievements and Challenges. Remote Sens. Environ. 2020, 241, 111716.
- Sist, M.; Schiavon, G.; Del Frate, F. A New Data Fusion Neural Network Scheme for Rainfall Retrieval Using Passive Microwave and Visible/Infrared Satellite Data. Appl. Sci. 2021, 11, 4686.
- Zhuo, L.; Han, D. Multi-Source Hydrological Soil Moisture State Estimation Using Data Fusion Optimisation. Hydrol. Earth Syst. Sci. 2017, 21, 3267–3285.
- Fehri, R.; Bogaert, P.; Khlifi, S.; Vanclooster, M. Data Fusion of Citizen-Generated Smartphone Discharge Measurements in Tunisia. J. Hydrol. 2020, 590, 125518.
- Abbaszadeh, P.; Moradkhani, H.; Zhan, X. Downscaling SMAP Radiometer Soil Moisture Over the CONUS Using an Ensemble Learning Method. Water Resour. Res. 2019, 55, 324–344.
- Serifi, A.; Günther, T.; Ban, N. Spatio-Temporal Downscaling of Climate Data Using Convolutional and Error-Predicting Neural Networks. Front. Clim. 2021, 3, 26.
- Sun, A.Y.; Tang, G. Downscaling Satellite and Reanalysis Precipitation Products Using Attention-Based Deep Convolutional Neural Nets. Front. Water 2020, 2, 56.
- Rittger, K.; Krock, M.; Kleiber, W.; Bair, E.H.; Brodzik, M.J.; Stephenson, T.R.; Rajagopalan, B.; Bormann, K.J.; Painter, T.H. Multi-Sensor Fusion Using Random Forests for Daily Fractional Snow Cover at 30 m. Remote Sens. Environ. 2021, 264, 112608.
- Tang, K.; Zhu, H.; Ni, P. Spatial Downscaling of Land Surface Temperature over Heterogeneous Regions Using Random Forest Regression Considering Spatial Features. Remote Sens. 2021, 13, 3645.
- Tran, H.; Nguyen, P.; Ombadi, M.; Hsu, K.; Sorooshian, S.; Qing, X. A Cloud-Free MODIS Snow Cover Dataset for the Contiguous United States from 2000 to 2017. Sci. Data 2019, 6, 180300.
- Miao, Q.; Pan, B.; Wang, H.; Hsu, K.; Sorooshian, S. Improving Monsoon Precipitation Prediction Using Combined Convolutional and Long Short Term Memory Neural Network. Water 2019, 11, 977.
- Lei, X.; Chen, W.; Panahi, M.; Falah, F.; Rahmati, O.; Uuemaa, E.; Kalantari, Z.; Ferreira, C.S.S.; Rezaie, F.; Tiefenbacher, J.P.; et al. Urban Flood Modeling Using Deep-Learning Approaches in Seoul, South Korea. J. Hydrol. 2021, 601, 126684.
- Veettil, A.V.; Konapala, G.; Mishra, A.K.; Li, H.-Y. Sensitivity of Drought Resilience-Vulnerability-Exposure to Hydrologic Ratios in Contiguous United States. J. Hydrol. 2018, 564, 294–306.
- Tran, H.; Nguyen, P.; Ombadi, M.; Hsu, K.; Sorooshian, S.; Andreadis, K. Improving Hydrologic Modeling Using Cloud-Free MODIS Flood Maps. J. Hydrometeorol. 2019, 20, 2203–2214.
- Mosavi, A.; Ozturk, P.; Chau, K. Flood Prediction Using Machine Learning Models: Literature Review. Water 2018, 10, 1536.
- Shahabi, H.; Shirzadi, A.; Ghaderi, K.; Omidvar, E.; Al-Ansari, N.; Clague, J.J.; Geertsema, M.; Khosravi, K.; Amini, A.; Bahrami, S.; et al. Flood Detection and Susceptibility Mapping Using Sentinel-1 Remote Sensing Data and a Machine Learning Approach: Hybrid Intelligence of Bagging Ensemble Based on K-Nearest Neighbor Classifier. Remote Sens. 2020, 12, 266.
- Lin, Q.; Leandro, J.; Wu, W.; Bhola, P.; Disse, M. Prediction of Maximum Flood Inundation Extents With Resilient Backpropagation Neural Network: Case Study of Kulmbach. Front. Earth Sci. 2020, 8, 332.
- Löwe, R.; Böhm, J.; Jensen, D.G.; Leandro, J.; Rasmussen, S.H. U-FLOOD—Topographic Deep Learning for Predicting Urban Pluvial Flood Water Depth. J. Hydrol. 2021, 603, 126898.
- Sahoo, S.; Russo, T.A.; Elliott, J.; Foster, I. Machine Learning Algorithms for Modeling Groundwater Level Changes in Agricultural Regions of the U.S. Water Resour. Res. 2017, 53, 3878–3895.
- Bui, D.T.; Panahi, M.; Shahabi, H.; Singh, V.P.; Shirzadi, A.; Chapi, K.; Khosravi, K.; Chen, W.; Panahi, S.; Li, S.; et al. Novel Hybrid Evolutionary Algorithms for Spatial Prediction of Floods. Sci. Rep. 2018, 8, 15364.
- Zhou, Y.; Guo, S.; Chang, F.-J. Explore an Evolutionary Recurrent ANFIS for Modelling Multi-Step-Ahead Flood Forecasts. J. Hydrol. 2019, 570, 343–355.
- Chang, F.-J.; Chiang, Y.-M.; Tsai, M.-J.; Shieh, M.-C.; Hsu, K.-L.; Sorooshian, S. Watershed Rainfall Forecasting Using Neuro-Fuzzy Networks with the Assimilation of Multi-Sensor Information. J. Hydrol. 2014, 508, 374–384.
- Araya, S.N.; Ghezzehei, T.A. Using Machine Learning for Prediction of Saturated Hydraulic Conductivity and Its Sensitivity to Soil Structural Perturbations. Water Resour. Res. 2019, 55, 5715–5737.
- Jian, J.; Shiklomanov, A.; Shuster, W.D.; Stewart, R.D. Predicting Near-Saturated Hydraulic Conductivity in Urban Soils. J. Hydrol. 2021, 595, 126051.
- Watt-Meyer, O.; Brenowitz, N.D.; Clark, S.K.; Henn, B.; Kwa, A.; McGibbon, J.; Perkins, W.A.; Bretherton, C.S. Correcting Weather and Climate Models by Machine Learning Nudged Historical Simulations. Geophys. Res. Lett. 2021, 48, e2021GL092555.
- Xu, T.; Liang, F. Machine Learning for Hydrologic Sciences: An Introductory Overview. WIREs Water 2021, 8, e1533.
- Koch, J.; Gotfredsen, J.; Schneider, R.; Troldborg, L.; Stisen, S.; Henriksen, H.J. High Resolution Water Table Modeling of the Shallow Groundwater Using a Knowledge-Guided Gradient Boosting Decision Tree Model. Front. Water 2021, 3.
- Wunsch, A.; Liesch, T.; Broda, S. Groundwater Level Forecasting with Artificial Neural Networks: A Comparison of Long Short-Term Memory (LSTM), Convolutional Neural Networks (CNNs), and Non-Linear Autoregressive Networks with Exogenous Input (NARX). Hydrol. Earth Syst. Sci. 2021, 25, 1671–1687.
- Zounemat-Kermani, M.; Matta, E.; Cominola, A.; Xia, X.; Zhang, Q.; Liang, Q.; Hinkelmann, R. Neurocomputing in Surface Water Hydrology and Hydraulics: A Review of Two Decades Retrospective, Current Status and Future Prospects. J. Hydrol. 2020, 588, 125085.
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–Runoff Modelling Using Long Short-Term Memory (LSTM) Networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022.
- Xu, W.; Jiang, Y.; Zhang, X.; Li, Y.; Zhang, R.; Fu, G. Using Long Short-Term Memory Networks for River Flow Prediction. Hydrol. Res. 2020, 51, 1358–1376.
- Li, P.; Zhang, J.; Krebs, P. Prediction of Flow Based on a CNN-LSTM Combined Deep Learning Approach. Water 2022, 14, 993.
- Xiang, Z.; Yan, J.; Demir, I. A Rainfall-Runoff Model With LSTM-Based Sequence-to-Sequence Learning. Water Resour. Res. 2020, 56, e2019WR025326.
- Lees, T.; Reece, S.; Kratzert, F.; Klotz, D.; Gauch, M.; De Bruijn, J.; Kumar Sahu, R.; Greve, P.; Slater, L.; Dadson, S.J. Hydrological Concept Formation inside Long Short-Term Memory (LSTM) Networks. Hydrol. Earth Syst. Sci. 2022, 26, 3079–3101.
- Hussain, D.; Hussain, T.; Khan, A.A.; Naqvi, S.A.A.; Jamil, A. A Deep Learning Approach for Hydrological Time-Series Prediction: A Case Study of Gilgit River Basin. Earth Sci. Inform. 2020, 13, 915–927.
- Anderson, S.; Radić, V. Evaluation and Interpretation of Convolutional Long Short-Term Memory Networks for Regional Hydrological Modelling. Hydrol. Earth Syst. Sci. 2022, 26, 795–825.
- Nourani, V.; Hosseini Baghanam, A.; Adamowski, J.; Kisi, O. Applications of Hybrid Wavelet–Artificial Intelligence Models in Hydrology: A Review. J. Hydrol. 2014, 514, 358–377.
- Ni, L.; Wang, D.; Singh, V.P.; Wu, J.; Wang, Y.; Tao, Y.; Zhang, J. Streamflow and Rainfall Forecasting by Two Long Short-Term Memory-Based Models. J. Hydrol. 2020, 583, 124296.
- Hosseiny, H.; Nazari, F.; Smith, V.; Nataraj, C. A Framework for Modeling Flood Depth Using a Hybrid of Hydraulics and Machine Learning. Sci. Rep. 2020, 10, 8222.
- Young, C.-C.; Liu, W.-C.; Wu, M.-C. A Physically Based and Machine Learning Hybrid Approach for Accurate Rainfall-Runoff Modeling during Extreme Typhoon Events. Appl. Soft Comput. 2017, 53, 205–216.
- Tamiru, H.; Dinka, M.O. Application of ANN and HEC-RAS Model for Flood Inundation Mapping in Lower Baro Akobo River Basin, Ethiopia. J. Hydrol. Reg. Stud. 2021, 36, 100855.
- Noori, N.; Kalin, L. Coupling SWAT and ANN Models for Enhanced Daily Streamflow Prediction. J. Hydrol. 2016, 533, 141–151.
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N. Prabhat Deep Learning and Process Understanding for Data-Driven Earth System Science. Nature 2019, 566, 195–204.
- Wagenaar, D.; Curran, A.; Balbi, M.; Bhardwaj, A.; Soden, R.; Hartato, E.; Mestav Sarica, G.; Ruangpan, L.; Molinario, G.; Lallemant, D. Invited Perspectives: How Machine Learning Will Change Flood Risk and Impact Assessment. Nat. Hazards Earth Syst. Sci. 2020, 20, 1149–1161.
- Williams, R.D.; Brasington, J.; Hicks, D.M. Numerical Modelling of Braided River Morphodynamics: Review and Future Challenges. Geogr. Compass 2016, 10, 102–127.
- Flora, K.; Khosronejad, A. On the Impact of Bed-Bathymetry Resolution and Bank Vegetation on the Flood Flow Field of the American River, California: Insights Gained Using Data-Driven Large-Eddy Simulation. J. Irrig. Drain. Eng. 2021, 147, 04021036.
- Coulthard, T.J.; Van De Wiel, M.J. Modelling River History and Evolution. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2012, 370, 2123–2142.
- Lane, S.N.; Ferguson, R.I. Modelling Reach-Scale Fluvial Flows. In Computational Fluid Dynamics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2005; pp. 215–269. ISBN 978-0-470-01519-3.
- Williams, R.D.; Measures, R.; Hicks, D.M.; Brasington, J. Assessment of a Numerical Model to Reproduce Event-Scale Erosion and Deposition Distributions in a Braided River. Water Resour. Res. 2016, 52, 6621–6642.
- Perrin, O.; Christophe, S.; Jacquinod, F.; Payrastre, O. Visual Analysis of Inconsistencies in Hydraulic Simulation Data. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Hannover, Germany, 25 August 2020; Copernicus GmbH: Goettingen, Germany, 2020; Volume XLIII-B4-2020, pp. 795–801.
- Mirza Alipour, S.; Leal, J. Emulation of 2D Hydrodynamic Flood Simulations at Catchment Scale Using ANN and SVR. Water 2021, 13, 2858.
- Ardourel, V.; Jebeile, J. Numerical Instability and Dynamical Systems. Eur. J. Philos. Sci. 2021, 11, 49.
- Hosseiny, H. A Deep Learning Model for Predicting River Flood Depth and Extent. Environ. Model. Softw. 2021, 145, 105186.
- Forghani, M.; Qian, Y.; Lee, J.; Farthing, M.W.; Hesser, T.; Kitanidis, P.K.; Darve, E.F. Application of Deep Learning to Large Scale Riverine Flow Velocity Estimation. Stoch. Environ. Res. Risk Assess. 2021, 35, 1069–1088.
- Cheng, C.; Zhang, G.-T. Deep Learning Method Based on Physics Informed Neural Network with Resnet Block for Solving Fluid Flow Problems. Water 2021, 13, 423.
- Fukami, K.; Fukagata, K.; Taira, K. Machine-Learning-Based Spatio-Temporal Super Resolution Reconstruction of Turbulent Flows. J. Fluid Mech. 2021, 909, 1–24.
- Buzzicotti, M.; Bonaccorso, F.; Di Leoni, P.C.; Biferale, L. Reconstruction of Turbulent Data with Deep Generative Models for Semantic Inpainting from TURB-Rot Database. Phys. Rev. Fluids 2021, 6, 050503.
- Baracchini, T.; Chu, P.Y.; Šukys, J.; Lieberherr, G.; Wunderle, S.; Wüest, A.; Bouffard, D. Data Assimilation of in Situ and Satellite Remote Sensing Data to 3D Hydrodynamic Lake Models: A Case Study Using Delft3D-FLOW v4.03 and OpenDA v2.4. Geosci. Model Dev. 2020, 13, 1267–1284.
- Carrassi, A.; Bocquet, M.; Bertino, L.; Evensen, G. Data Assimilation in the Geosciences: An Overview of Methods, Issues, and Perspectives. WIREs Clim. Chang. 2018, 9, e535.
- Houser, P.; Lannoy, G.; Walker, J. Hydrologic Data Assimilation. In Advances in Water Science Methodologies; CRC Press: Boca Raton, FL, USA, 2012; ISBN 978-953-51-0294-6.
- Nearing, G.S.; Kratzert, F.; Sampson, A.K.; Pelissier, C.S.; Klotz, D.; Frame, J.M.; Prieto, C.; Gupta, H.V. What Role Does Hydrological Science Play in the Age of Machine Learning? Water Resour. Res. 2021, 57, e2020WR028091.
- Xiong, Z.; Sang, J.; Sun, X.; Zhang, B.; Li, J. Comparisons of Performance Using Data Assimilation and Data Fusion Approaches in Acquiring Precipitable Water Vapor: A Case Study of a Western United States of America Area. Water 2020, 12, 2943.
- Farchi, A.; Laloyaux, P.; Bonavita, M.; Bocquet, M. Using Machine Learning to Correct Model Error in Data Assimilation and Forecast Applications. Q. J. R. Meteorol. Soc. 2021, 147, 3067–3084.
- Arcucci, R.; Zhu, J.; Hu, S.; Guo, Y.-K. Deep Data Assimilation: Integrating Deep Learning with Data Assimilation. Appl. Sci. 2021, 11, 1114.
- Geer, A. Learning Earth System Models from Observations: Machine Learning or Data Assimilation? Philos. Trans. R. Soc. A 2021, 379, 20200089.
- Boucher, M.-A.; Quilty, J.; Adamowski, J. Data Assimilation for Streamflow Forecasting Using Extreme Learning Machines and Multilayer Perceptrons. Water Resour. Res. 2020, 56, e2019WR026226.
- Wagener, T.; Boyle, D.P.; Lees, M.J.; Wheater, H.S.; Gupta, H.V.; Sorooshian, S. A Framework for Development and Application of Hydrological Models. Hydrol. Earth Syst. Sci. 2001, 5, 13–26.
- Vrugt, J.A.; Stauffer, P.H.; Wöhling, T.; Robinson, B.A.; Vesselinov, V.V. Inverse Modeling of Subsurface Flow and Transport Properties: A Review with New Developments. Vadose Zone J. 2008, 7, 843–864.
- Carrera, J.; Alcolea, A.; Medina, A.; Hidalgo, J.; Slooten, L.J. Inverse Problem in Hydrogeology. Hydrogeol. J. 2005, 13, 206–222.
- Beven, K. A Manifesto for the Equifinality Thesis. J. Hydrol. 2006, 320, 18–36.
- Vrugt, J.A.; Gupta, H.V.; Bastidas, L.A.; Bouten, W.; Sorooshian, S. Effective and Efficient Algorithm for Multiobjective Optimization of Hydrologic Models. Water Resour. Res. 2003, 39, 1–19.
- Wolpert, D.H.; Macready, W.G. No Free Lunch Theorems for Optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82.
- Yusoff, Y.; Ngadiman, M.S.; Zain, A.M. Overview of NSGA-II for Optimizing Machining Process Parameters. Procedia Eng. 2011, 15, 3978–3983.
- Ibrahim, K.S.M.H.; Huang, Y.F.; Ahmed, A.N.; Koo, C.H.; El-Shafie, A. A Review of the Hybrid Artificial Intelligence and Optimization Modelling of Hydrological Streamflow Forecasting. Alex. Eng. J. 2022, 61, 279–303.
- Bianchi, L.; Dorigo, M.; Gambardella, L.M.; Gutjahr, W.J. A Survey on Metaheuristics for Stochastic Combinatorial Optimization. Nat. Comput. 2009, 8, 239–287.
- Vrugt, J.A.; Robinson, B.A. Improved Evolutionary Optimization from Genetically Adaptive Multimethod Search. Proc. Natl. Acad. Sci. USA 2007, 104, 708–711.
- Zhang, X.; Srinivasan, R.; Liew, M.V. On the Use of Multi-Algorithm, Genetically Adaptive Multi-Objective Method for Multi-Site Calibration of the SWAT Model. Hydrol. Process. 2010, 24, 955–969.
- Confesor, R.B., Jr.; Whittaker, G.W. Automatic Calibration of Hydrologic Models With Multi-Objective Evolutionary Algorithm and Pareto Optimization1. JAWRA J. Am. Water Resour. Assoc. 2007, 43, 981–989.
- Ercan, M.B.; Goodall, J.L. Design and Implementation of a General Software Library for Using NSGA-II with SWAT for Multi-Objective Model Calibration. Environ. Model. Softw. 2016, 84, 112–120.
- Tsai, W.-P.; Feng, D.; Pan, M.; Beck, H.; Lawson, K.; Yang, Y.; Liu, J.; Shen, C. From Calibration to Parameter Learning: Harnessing the Scaling Effects of Big Data in Geoscientific Modeling. Nat. Commun. 2021, 12, 5988.
- Krapu, C.; Borsuk, M.; Kumar, M. Gradient-Based Inverse Estimation for a Rainfall-Runoff Model. Water Resour. Res. 2019, 55, 6625–6639.
- Saravanan, V.S.; McDonald, G.T.; Mollinga, P.P. Critical Review of Integrated Water Resources Management: Moving beyond Polarised Discourse. Nat. Resour. Forum 2009, 33, 76–86.
- Sun, R.; Hernández, F.; Liang, X.; Yuan, H. A Calibration Framework for High-Resolution Hydrological Models Using a Multiresolution and Heterogeneous Strategy. Water Resour. Res. 2020, 56, e2019WR026541.
- Ahmad, A.; El-Shafie, A.; Razali, S.F.M.; Mohamad, Z.S. Reservoir Optimization in Water Resources: A Review. Water Resour. Manag. 2014, 28, 3391–3405.
- Xiang, X.; Li, Q.; Khan, S.; Khalaf, O.I. Urban Water Resource Management for Sustainable Environment Planning Using Artificial Intelligence Techniques. Environ. Impact Assess. Rev. 2021, 86, 106515.
- Chaves, P.; Chang, F.-J. Intelligent Reservoir Operation System Based on Evolving Artificial Neural Networks. Adv. Water Resour. 2008, 31, 926–936.
- Cai, Y.; Wang, H.; Yue, W.; Xie, Y.; Liang, Q. An Integrated Approach for Reducing Spatially Coupled Water-Shortage Risks of Beijing-Tianjin-Hebei Urban Agglomeration in China. J. Hydrol. 2021, 603, 127123.
- Zhang, D.; Peng, Q.; Lin, J.; Wang, D.; Liu, X.; Zhuang, J. Simulating Reservoir Operation Using a Recurrent Neural Network Algorithm. Water 2019, 11, 865.
- Zarei, M.; Bozorg-Haddad, O.; Baghban, S.; Delpasand, M.; Goharian, E.; Loáiciga, H.A. Machine-Learning Algorithms for Forecast-Informed Reservoir Operation (FIRO) to Reduce Flood Damages. Sci. Rep. 2021, 11, 24295.
- Navarro-Hellín, H.; Martínez-del-Rincon, J.; Domingo-Miguel, R.; Soto-Valles, F.; Torres-Sánchez, R. A Decision Support System for Managing Irrigation in Agriculture. Comput. Electron. Agric. 2016, 124, 121–131.
- Munawar, H.S.; Hammad, A.W.A.; Waller, S.T.; Thaheem, M.J.; Shrestha, A. An Integrated Approach for Post-Disaster Flood Management Via the Use of Cutting-Edge Technologies and UAVs: A Review. Sustainability 2021, 13, 7925.
- Abraham, A. Adaptation of Fuzzy Inference System Using Neural Learning. In Fuzzy Systems Engineering: Theory and Practice; Nedjah, N., de Macedo Mourelle, L., Eds.; Studies in Fuzziness and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2005; pp. 53–83. ISBN 978-3-540-32397-6.
- Ighalo, J.O.; Adeniyi, A.G.; Marques, G. Internet of Things for Water Quality Monitoring and Assessment: A Comprehensive Review. In Artificial Intelligence for Sustainable Development: Theory, Practice and Future Applications; Hassanien, A.E., Bhatnagar, R., Darwish, A., Eds.; Studies in Computational Intelligence; Springer International Publishing: Cham, Switzerland, 2021; pp. 245–259. ISBN 978-3-030-51920-9.
- Jan, F.; Min-Allah, N.; Düştegör, D. IoT Based Smart Water Quality Monitoring: Recent Techniques, Trends and Challenges for Domestic Applications. Water 2021, 13, 1729.
- Leigh, C.; Kandanaarachchi, S.; McGree, J.M.; Hyndman, R.J.; Alsibai, O.; Mengersen, K.; Peterson, E.E. Predicting Sediment and Nutrient Concentrations from High-Frequency Water-Quality Data. PLoS ONE 2019, 14, e0215503.
- Mathany, T.M.; Saraceno, J.F.; Kulongoski, J.T. Guidelines and Standard Procedures for High-Frequency Groundwater-Quality Monitoring Stations—Design, Operation, and Record Computation; Techniques and Methods; U.S. Geological Survey: Reston, VA, USA, 2019; Volume 1-D7, p. 66.
- Seifert-Dähnn, I.; Furuseth, I.S.; Vondolia, G.K.; Gal, G.; de Eyto, E.; Jennings, E.; Pierson, D. Costs and Benefits of Automated High-Frequency Environmental Monitoring—The Case of Lake Water Management. J. Environ. Manag. 2021, 285, 112108.
- Jung, H.; Senf, C.; Jordan, P.; Krueger, T. Benchmarking Inference Methods for Water Quality Monitoring and Status Classification. Environ. Monit. Assess. 2020, 192, 261.
- Jesus, G.; Casimiro, A.; Oliveira, A. A Survey on Data Quality for Dependable Monitoring in Wireless Sensor Networks. Sensors 2017, 17, 2010.
- Khatri, P.; Gupta, K.K.; Gupta, R.K. Drift Compensation of Commercial Water Quality Sensors Using Machine Learning to Extend the Calibration Lifetime. J. Ambient Intell. Humaniz. Comput. 2021, 12, 3091–3099.
- Kahiluoto, J.; Hirvonen, J.; Näykki, T. Automatic Real-Time Uncertainty Estimation for Online Measurements: A Case Study on Water Turbidity. Environ. Monit. Assess. 2019, 191, 259.
- Rodriguez-Perez, J.; Leigh, C.; Liquet, B.; Kermorvant, C.; Peterson, E.; Sous, D.; Mengersen, K. Detecting Technical Anomalies in High-Frequency Water-Quality Data Using Artificial Neural Networks. Environ. Sci. Technol. 2020, 54, 13719–13730.
- Jiang, J.; Tang, S.; Han, D.; Fu, G.; Solomatine, D.; Zheng, Y. A Comprehensive Review on the Design and Optimization of Surface Water Quality Monitoring Networks. Environ. Model. Softw. 2020, 132, 104792.
- Chachuła, K.; Słojewski, T.M.; Nowak, R. Multisensor Data Fusion for Localization of Pollution Sources in Wastewater Networks. Sensors 2022, 22, 387.
- Cao, H.; Guo, Z.; Wang, S.; Cheng, H.; Zhan, C. Intelligent Wide-Area Water Quality Monitoring and Analysis System Exploiting Unmanned Surface Vehicles and Ensemble Learning. Water 2020, 12, 681.
- Huang, W.; Yang, Y. Water Quality Sensor Model Based on an Optimization Method of RBF Neural Network. Comput. Water Energy Environ. Eng. 2019, 9, 1.
- Jafari, H.; Rajaee, T.; Kisi, O. Improved Water Quality Prediction with Hybrid Wavelet-Genetic Programming Model and Shannon Entropy. Nat. Resour. Res. 2020, 29, 3819–3840.
- Jiang, Y.; Li, C.; Sun, L.; Guo, D.; Zhang, Y.; Wang, W. A Deep Learning Algorithm for Multi-Source Data Fusion to Predict Water Quality of Urban Sewer Networks. J. Clean. Prod. 2021, 318, 128533.
- Pattnaik, B.S.; Pattanayak, A.S.; Udgata, S.K.; Panda, A.K. Machine Learning Based Soft Sensor Model for BOD Estimation Using Intelligence at Edge. Complex Intell. Syst. 2021, 7, 961–976.
- Chen, K.; Chen, H.; Zhou, C.; Huang, Y.; Qi, X.; Shen, R.; Liu, F.; Zuo, M.; Zou, X.; Wang, J.; et al. Comparative Analysis of Surface Water Quality Prediction Performance and Identification of Key Water Parameters Using Different Machine Learning Models Based on Big Data. Water Res. 2020, 171, 115454.
- Castrillo, M.; García, Á.L. Estimation of High Frequency Nutrient Concentrations from Water Quality Surrogates Using Machine Learning Methods. Water Res. 2020, 172, 115490.
- Chang, N.-B.; Bai, K.; Chen, C.-F. Integrating Multisensor Satellite Data Merging and Image Reconstruction in Support of Machine Learning for Better Water Quality Management. J. Environ. Manag. 2017, 201, 227–240.
- Hamshaw, S.D.; Dewoolkar, M.M.; Schroth, A.W.; Wemple, B.C.; Rizzo, D.M. A New Machine-Learning Approach for Classifying Hysteresis in Suspended-Sediment Discharge Relationships Using High-Frequency Monitoring Data. Water Resour. Res. 2018, 54, 4040–4058.
- Rajaee, T.; Khani, S.; Ravansalar, M. Artificial Intelligence-Based Single and Hybrid Models for Prediction of Water Quality in Rivers: A Review. Chemom. Intell. Lab. Syst. 2020, 200, 103978.
- Naloufi, M.; Lucas, F.S.; Souihi, S.; Servais, P.; Janne, A.; Wanderley Matos De Abreu, T. Evaluating the Performance of Machine Learning Approaches to Predict the Microbial Quality of Surface Waters and to Optimize the Sampling Effort. Water 2021, 13, 2457.
- Chen, Y.; Song, L.; Liu, Y.; Yang, L.; Li, D. A Review of the Artificial Neural Network Models for Water Quality Prediction. Appl. Sci. 2020, 10, 5776.
- Shi, P.; Li, G.; Yuan, Y.; Kuang, L. Data Fusion Using Improved Support Degree Function in Aquaculture Wireless Sensor Networks. Sensors 2018, 18, 3851.
- Bui, D.T.; Khosravi, K.; Tiefenbacher, J.; Nguyen, H.; Kazakis, N. Improving Prediction of Water Quality Indices Using Novel Hybrid Machine-Learning Algorithms. Sci. Total Environ. 2020, 721, 137612.
- Shen, L.Q.; Amatulli, G.; Sethi, T.; Raymond, P.; Domisch, S. Estimating Nitrogen and Phosphorus Concentrations in Streams and Rivers, within a Machine Learning Framework. Sci. Data 2020, 7, 161.
- Sperotto, A.; Molina, J.L.; Torresan, S.; Critto, A.; Pulido-Velazquez, M.; Marcomini, A. A Bayesian Networks Approach for the Assessment of Climate Change Impacts on Nutrients Loading. Environ. Sci. Policy 2019, 100, 21–36.
- Song, C.; Yao, L.; Hua, C.; Ni, Q. A Novel Hybrid Model for Water Quality Prediction Based on Synchrosqueezed Wavelet Transform Technique and Improved Long Short-Term Memory. J. Hydrol. 2021, 603, 126879.
- Najah Ahmed, A.; Binti Othman, F.; Abdulmohsin Afan, H.; Khaleel Ibrahim, R.; Ming Fai, C.; Shabbir Hossain, M.; Ehteram, M.; Elshafie, A. Machine Learning Methods for Better Water Quality Prediction. J. Hydrol. 2019, 578, 124084.
- Zhou, J.; Chu, F.; Li, X.; Ma, H.; Xiao, F.; Sun, L. Water Quality Prediction Approach Based on T-SNE and SA-BiLSTM. In Proceedings of the 2020 IEEE 22nd International Conference on High Performance Computing and Communications; IEEE 18th International Conference on Smart City; IEEE 6th International Conference on Data Science and Systems (HPCC/SmartCity/DSS), Yanuca Island, Fiji, 14–16 December 2020; pp. 708–714.
- Milošević, D.; Medeiros, A.S.; Stojković Piperac, M.; Cvijanović, D.; Soininen, J.; Milosavljević, A.; Predić, B. The Application of Uniform Manifold Approximation and Projection (UMAP) for Unconstrained Ordination and Classification of Biological Indicators in Aquatic Ecology. Sci. Total Environ. 2022, 815, 152365.
- Noori, N.; Kalin, L.; Isik, S. Water Quality Prediction Using SWAT-ANN Coupled Approach. J. Hydrol. 2020, 590, 125220.
- Hanson, P.C.; Stillman, A.B.; Jia, X.; Karpatne, A.; Dugan, H.A.; Carey, C.C.; Stachelek, J.; Ward, N.K.; Zhang, Y.; Read, J.S.; et al. Predicting Lake Surface Water Phosphorus Dynamics Using Process-Guided Machine Learning. Ecol. Model. 2020, 430, 109136.
- Green, M.B.; Pardo, L.H.; Bailey, S.W.; Campbell, J.L.; McDowell, W.H.; Bernhardt, E.S.; Rosi, E.J. Predicting High-Frequency Variation in Stream Solute Concentrations with Water Quality Sensors and Machine Learning. Hydrol. Process. 2021, 35, e14000.
- Baker, V.R. The Modern Evolution of Geomorphology—Binghamton and Personal Perspectives, 1970–2019 and Beyond. Geomorphology 2020, 366, 106684.
- Flener, C.; Vaaja, M.; Jaakkola, A.; Krooks, A.; Kaartinen, H.; Kukko, A.; Kasvi, E.; Hyyppä, H.; Hyyppä, J.; Alho, P. Seamless Mapping of River Channels at High Resolution Using Mobile LiDAR and UAV-Photography. Remote Sens. 2013, 5, 6382–6407.
- Tonina, D.; McKean, J.A.; Benjankar, R.M.; Wright, C.W.; Goode, J.R.; Chen, Q.; Reeder, W.J.; Carmichael, R.A.; Edmondson, M.R. Mapping River Bathymetries: Evaluating Topobathymetric LiDAR Survey. Earth Surf. Process. Landf. 2019, 44, 507–520.
- Emanuele, P.; Nives, G.; Andrea, C.; Carlo, C.; Paolo, D.; Andrea Maria, L. Bathymetric Detection of Fluvial Environments through UASs and Machine Learning Systems. Remote Sens. 2020, 12, 4148.
- Carbonneau, P.E.; Dugdale, S.J.; Breckon, T.P.; Dietrich, J.T.; Fonstad, M.A.; Miyamoto, H.; Woodget, A.S. Adopting Deep Learning Methods for Airborne RGB Fluvial Scene Classification. Remote Sens. Environ. 2020, 251, 112107.
- Rivas Casado, M.; Ballesteros Gonzalez, R.; Kriechbaumer, T.; Veal, A. Automated Identification of River Hydromorphological Features Using UAV High Resolution Aerial Imagery. Sensors 2015, 15, 27969–27989.
- Demarchi, L.; van de Bund, W.; Pistocchi, A. Object-Based Ensemble Learning for Pan-European Riverscape Units Mapping Based on Copernicus VHR and EU-DEM Data Fusion. Remote Sens. 2020, 12, 1222.
- Ling, F.; Boyd, D.; Ge, Y.; Foody, G.M.; Li, X.; Wang, L.; Zhang, Y.; Shi, L.; Shang, C.; Li, X.; et al. Measuring River Wetted Width From Remotely Sensed Imagery at the Subpixel Scale With a Deep Convolutional Neural Network. Water Resour. Res. 2019, 55, 5631–5649.
- Guillon, H.; Byrne, C.F.; Lane, B.A.; Solis, S.S.; Pasternack, G.B. Machine Learning Predicts Reach-Scale Channel Types From Coarse-Scale Geospatial Data in a Large River Basin. Water Resour. Res. 2020, 56, e2019WR026691.
- Heasley, E.L.; Millington, J.D.A.; Clifford, N.J.; Chadwick, M.A. A Waterbody Typology Derived from Catchment Controls Using Self-Organising Maps. Water 2020, 12, 78.
- Guneralp, I.; Filippi, A.M.; Hales, B. Influence of River Channel Morphology and Bank Characteristics on Water Surface Boundary Delineation Using High-Resolution Passive Remote Sensing and Template Matching. Earth Surf. Process. Landf. 2014, 39, 977–986.
- Moody, D.I.; Brumby, S.P.; Rowland, J.C.; Gangodagamage, C. Undercomplete Learned Dictionaries for Land Cover Classification in Multispectral Imagery of Arctic Landscapes Using CoSA: Clustering of Sparse Approximations. In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery Xix; Shen, S.S., Lewis, P.E., Eds.; SPIE: Baltimore, MD, USA, 2013; Volume 8743, ISBN 978-0-8194-9534-1.
- Corenblit, D.; Vautier, F.; González, E.; Steiger, J. Formation and Dynamics of Vegetated Fluvial Landforms Follow the Biogeomorphological Succession Model in a Channelized River. Earth Surf. Process. Landf. 2020, 45, 2020–2035.
- Díaz Gómez, R.; Pasternack, G.B.; Guillon, H.; Byrne, C.F.; Schwindt, S.; Larrieu, K.G.; Solis, S.S. Mapping Subaerial Sand-Gravel-Cobble Fluvial Sediment Facies Using Airborne Lidar and Machine Learning. Geomorphology 2022, 401, 108106.
- Khan, S.; Fryirs, K.A. Application of Globally Available, Coarse-Resolution Digital Elevation Models for Delineating Valley Bottom Segments of Varying Length across a Catchment. Earth Surf. Process. Landf. 2020, 45, 2788–2803.
- Clubb, F.J.; Bookhagen, B.; Rheinwalt, A. Clustering River Profiles to Classify Geomorphic Domains. J. Geophys. Res. Earth Surf. 2019, 124, 1417–1439.
- Demarchi, L.; Bizzi, S.; Piegay, H. Hierarchical Object-Based Mapping of Riverscape Units and in-Stream Mesohabitats Using LiDAR and VHR Imagery. Remote Sens. 2016, 8, 97.
- Harrison, L.R.; Legleiter, C.J.; Overstreet, B.T.; Bell, T.W.; Hannon, J. Assessing the Potential for Spectrally Based Remote Sensing of Salmon Spawning Locations. River Res. Appl. 2020, 36, 1618–1632.
- Alfredsen, K.; Dalsgård, A.; Shamsaliei, S.; Halleraker, J.H.; Gundersen, O.E. Towards an Automatic Characterization of Riverscape Development by Deep Learning. River Res. Appl. 2022, 38, 810–816.
- González-Castro, J.A.; Muste, M. Framework for Estimating Uncertainty of ADCP Measurements from a Moving Boat by Standardized Uncertainty Analysis. J. Hydraul. Eng. 2007, 133, 1390–1410.
- Pan, Z.; Glennie, C.; Hartzell, P.; Fernandez-Diaz, J.C.; Legleiter, C.; Overstreet, B. Performance Assessment of High Resolution Airborne Full Waveform LiDAR for Shallow River Bathymetry. Remote Sens. 2015, 7, 5133–5159.
- Bandini, F.; Olesen, D.; Jakobsen, J.; Kittel, C.M.M.; Wang, S.; Garcia, M.; Bauer-Gottwein, P. Technical Note: Bathymetry Observations of Inland Water Bodies Using a Tethered Single-Beam Sonar Controlled by an Unmanned Aerial Vehicle. Hydrol. Earth Syst. Sci. 2018, 22, 4165–4181.
- Mandlburger, G.; Kölle, M.; Nübel, H.; Soergel, U. BathyNet: A Deep Neural Network for Water Depth Mapping from Multispectral Aerial Images. PFG—J. Photogramm. Remote Sens. Geoinf. Sci. 2021, 89, 71–89.
- Alvarez, L.V.; Moreno, H.A.; Segales, A.R.; Pham, T.G.; Pillar-Little, E.A.; Chilson, P.B. Merging Unmanned Aerial Systems (UAS) Imagery and Echo Soundings with an Adaptive Sampling Technique for Bathymetric Surveys. Remote Sens. 2018, 10, 1362.
- Van Iersel, W.; Straatsma, M.; Middelkoop, H.; Addink, E. Multitemporal Classification of River Floodplain Vegetation Using Time Series of UAV Images. Remote Sens. 2018, 10, 1144.
- Hemmelder, S.; Marra, W.; Markies, H.; De Jong, S.M. Monitoring River Morphology & Bank Erosion Using UAV Imagery—A Case Study of the River Buëch, Hautes-Alpes, France. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 428–437.
- Boothroyd, R.J.; Williams, R.D.; Hoey, T.B.; Barrett, B.; Prasojo, O.A. Applications of Google Earth Engine in Fluvial Geomorphology for Detecting River Channel Change. WIREs Water 2021, 8, e21496.
- Shi, W.; Zhang, M.; Zhang, R.; Chen, S.; Zhan, Z. Change Detection Based on Artificial Intelligence: State-of-the-Art and Challenges. Remote Sens. 2020, 12, 1688.
- Wheaton, J.M.; Fryirs, K.A.; Brierley, G.; Bangen, S.G.; Bouwes, N.; O’Brien, G. Geomorphic Mapping and Taxonomy of Fluvial Landforms. Geomorphology 2015, 248, 273–295.
- Polidori, L.; El Hage, M. Digital Elevation Model Quality Assessment Methods: A Critical Review. Remote Sens. 2020, 12, 3522.
- Carbonneau, P.E.; Belletti, B.; Micotti, M.; Lastoria, B.; Casaioli, M.; Mariani, S.; Marchetti, G.; Bizzi, S. UAV-Based Training for Fully Fuzzy Classification of Sentinel-2 Fluvial Scenes. Earth Surf. Process. Landf. 2020, 45, 3120–3140.
This entry is offline, you can click here to edit this entry!
