Optical Properties of Plasmonic Metal Nanoparticles: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Contributor:
Caterina Serafinelli
,
Alessandro Fantoni
,
Elisabete C. B. A. Alegria
,
Manuela Vieira

Plasmonic phenomena and materials have been extensively investigated for a long time and gained popularity in the last few years, finding in the design of the biosensors platforms promising applications offering devices with excellent performances. Hybrid systems composed of graphene, or other 2D materials, and plasmonic metal nanostructures present extraordinary optical properties originated from the synergic connection between plasmonic optical effects and the unusual physicochemical properties of 2D materials, thus improving their application in a broad range of fields. 

  • 2D nanomaterials
  • metal nanoparticles
  • hybrid nanocomposites
  • plasmonics

1. Physics and Working Principles of Plasmon Resonance

The interaction of the electromagnetic field with an interface can generate appealing surface excitations. When the free electrons of a metal are coupled in resonance with the electromagnetic field of the radiation, surface-bound EM modes can be originated that are called surface plasmons (SPs). Usually, SPs are originated at the interface between a noble metal and a dielectric, thus satisfying the condition for the SPs excitation that requires two materials with optical constants of opposite signs connecting each other [1]. Often, SPs are classified in two categories: propagating surface plasmons (PSPs) and localized surface plasmons (LSPs) [2]. The physics and working principles behind the two classes of SPs will be revisited.

2. Propagating Surface Plasmon Resonances (PSPR)

The first type of surface plasmon consists of running surface waves called propagating surface plasmons (PSPs): when a p-polarized light (radiation with its electric vector parallel to the plane of incidence, namely the plane perpendicular to the surface containing the incident and reflected wavevectors [3]) interacts with a metal surface, the free electrons in the metal react collectively, starting to oscillate in resonance with the light wave and propagate along the interface between metal nanostructures and dielectrics [4]. In this context, SPPs can be considered as light waves entrapped on the conducting material surface. The magnetic vector of PSPs is parallel to the plane of the interface and perpendicular to the direction of propagation of the wave, so that they can be referred as a transverse-magnetic (TM) polarized mode [5]. Because of their combined character between electromagnetic wave and surface charge, the SPWs should be termed surface plasmon polaritons (SPPs) to reflect the hybrid nature. As a consequence of the hybrid nature and in contrast to the propagating nature of PSPs along the surface, the EM field component perpendicular to the surface is maximum near the metal surface and decays exponentially at growing distances from it [6], so that in the dielectric medium at the top of the metal, the decay length of the field, δd, is of the order of half the wavelength of light involved, whereas the decay length into the metal, dm, is determined by the skin depth (Figure 1A). This means that most of the EM field is concentrated in the dielectric medium close to the metal surface, showing a typical penetration depth δd between 50 and 500 nm when working in visible or near-infrared (NIR) wavelengths. As a result, only the changes in refractive index occurring within the evanescent field are able to modify the SPP propagation and be detected, and this is relevant for SPRs analysis in view of the fact that biorecognition events taking place on the metal surface can be detected by exploring certain properties of the reflected light, such as angle, intensity or wavelengths. When the light vector is coupled to the surface plasmon such that the component of the light wavevector parallel to the interface matches the propagation vector of the SPP, the excitation of SPPs is reached, which is followed by a sharp dip in reflectance [4]. The dependence of the propagation vector on the refractive index of the dielectric is expressed by the SP dispersion relation [5], namely the frequency-dependent SP wavevector calculated by solving the Maxwell equation with appropriate boundary conditions, thus obtaining:
k x SPP = ω c ε 2 ( ω ) ε d ε 2 ( ω ) + ε d
where KxSPP is the wavevector component of SPP propagation, and εd is the dielectric constant of the medium, which is directly related to the refractive index of the materials by the equation
εd = n2
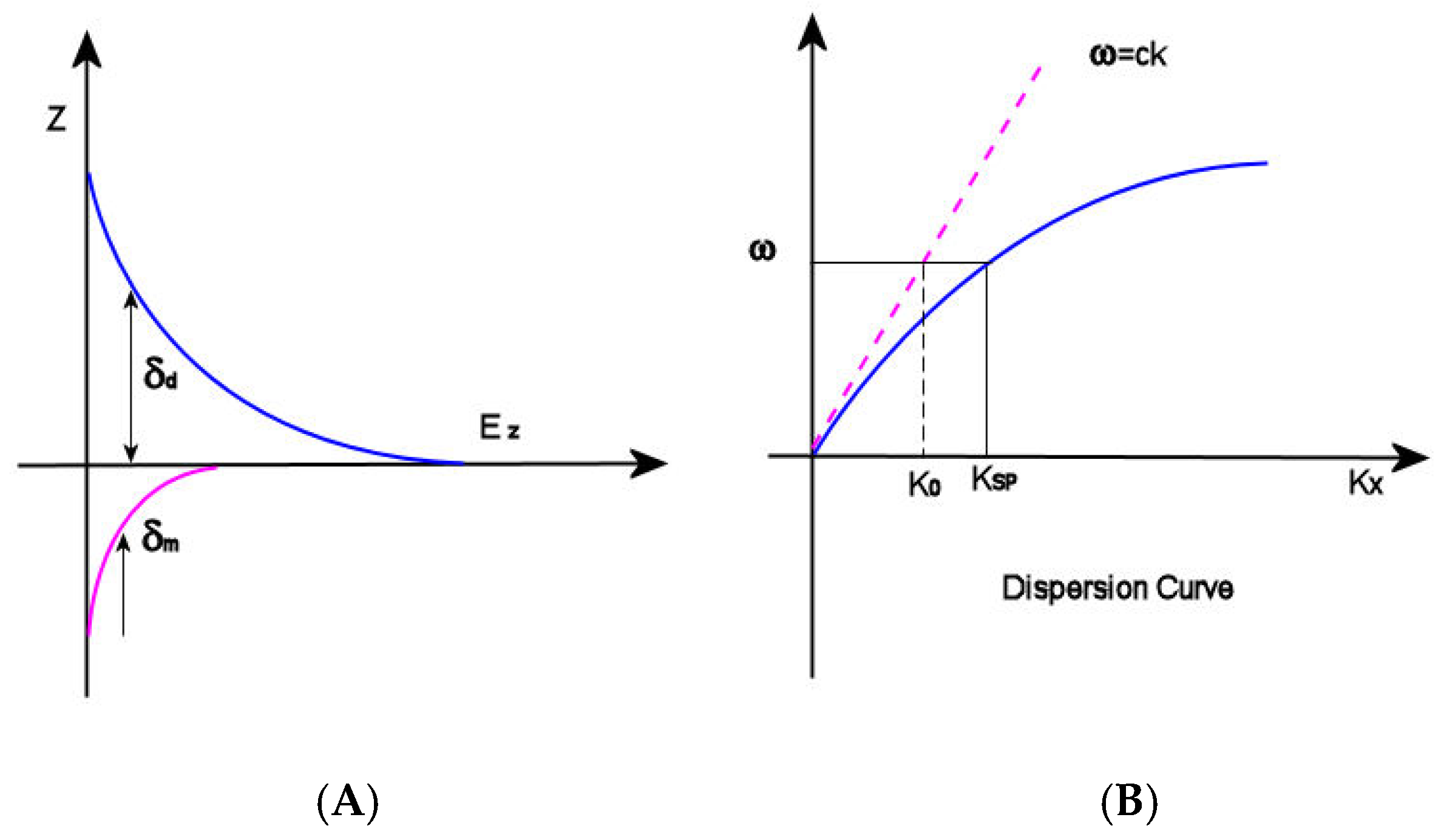
Figure 1. (A) δd (decay length of the field) and δm (decay length into the metal); (B) dispersion curve for an SP mode showing the momentum mismatch issue.
ε(ω) is complex dielectric function of the metal depending on the frequency
ε(ω) = ε1(ω) + iε2(ω)
and ω and c are the angular frequency and the speed of light in a vacuum, respectively. Observing the dispersion curve (Figure 1B), the excitation of surface plasmon polaritons can be explored: the SP mode always lies beyond the light line, that is, it has greater momentum (ℏkSP) than a free space photon (ℏk0) of the same frequency ω [6]. In this condition, the incident light cannot easily excite the surface plasmon polaritons: in order to achieve SPRs excitation, therefore, the resulting momentum mismatch between light and SPs of the same frequency must be overcome by enlarging the wavevector of the excitation light.
On this basis, the optical configurations for SPR analysis are classified according to SPP excitation method or the detection scheme [5]. The most common schemes are: (1) the prism coupled Kretschmann configuration, where an evanescent wave penetrating the metal film is generated by the light that is totally reflected at the base of a high refractive index glass prism when passing across it. The propagation vector of the evanescent wave can be adjusted by controlling the angle of incidence so that it mismatches that of SPPs; (2) the grating couplers, based on the light waves diffraction: in this case, the wavevector component of the diffracted light that is parallel to the interface is increased for a value inversely proportional to the period of the grating, so that can be matched with that of SPPs; (3) waveguide structures: when the light vector is coupled to the surface plasmon such that the component of the light wavevector parallel to the interface matches the propagation vector of the SPP, the excitation of SPPs is reached, which is followed by a sharp dip in reflectance. Due to the great potential of SPR analysis, much research has been performed in the last few years to develop enhanced SPR structures [7]; however, the use of hybrid plasmonic metal nanoparticles and 2D nanomaterials is only in its early stage. For the first time, a highly sensitive surface plasmon resonance (SPR) biosensor based on AuNPs/MoS2 hybrid nanostructures for microRNA (miRNA) detection has been presented by Nie et al. [8]. The sensing platform has been produced following a two-step protocol: in the first stage, the captured DNA consisting of a thiol-modified probe including a sequence complementary to the target miRNA has been immobilized on the Au film, and then, DNA-linked AuNPs/MoS2 nanocomposites were used to combine with the other section of the miRNA-141, thus creating a sandwich structure. The sensing platform has been exploited in SPR analysis, detecting the resonance angle in the presence of a different concentration of miRNA-141. The so-developed sensing system displayed high sensitivity toward miRNA detection, where the improved performances originated from the presence of AuNPs/MoS2 nanohybrids. The signal amplification of the structure has been assigned to three main causes: the first cause is the synergistic effect of LSPR of AuNPs on SPR waves, whereas the second one is a larger number of AuNPs in the system due to the presence of MoS2 nanosheets and finally, SPR in AuNPs-MoS2 nanocomposites could be actively controlled by the photoexcited excitons, resulting in an enhancement of SPR signal. As a consequence of the signal amplification due to the presence of the AuNPs/MoS2 hybrids in the sensing system, the very lower limit of detection (LOD) of 0.5 fM has been reached. The additional advantages of the developed sensing platform are its high specificity, acceptable reproducibility, and precision; furthermore, the system is low-cost and enzyme-free. The SPR assay based on AuNPs/MoS2 has been exploited also to detect human miRNA from cancer cells with excellent results, thus providing great potential for miRNA quantification in clinical diagnosis and disease treatment.

3. Localized Surface Plasmon Resonances (LSPR)

The interaction of the light with subwavelength-sized metallic particles emerges in the non-propagating collective oscillations of the particle conduction electrons, which are named localized surface plasmon resonance (LSPR). As a result of the LSPR, there is an accumulation of charges on the particle surface functioning as a dipole. The presence of LSPR acting as an oscillating dipole in a nanoparticle is the basis of two phenomena. Firstly, the optical extinction of the particle reaches its maximum value at the frequency of plasmon resonance, taking place in the visible range for noble metal nanoparticles. Secondly, the electromagnetic fields localized close to the particle surface are largely enhanced, with the enhancement being higher at the surface and quickly decreasing when the distance becomes greater. In order to reach a deeper understanding on the LSPR origins, the scattering theory must be considered as well as the interactions between the spherical nanoparticle and the light discussed in view of Mie Theory [9]. In the famous paper published in 1908 [10], Gustav Mie illustrated a first overview on how to calculate the scattering and absorption of light by spherical particles, developing an analytical solution to Maxwell’s equations. By means of his calculations, he was able to explain the color of gold colloids changing with the size of gold spheres, which was a phenomenon later interpreted considering surface plasmon resonances. When the diameter of metallic spherical nanoparticles is much smaller than the incident light wavelength (Ø << λ where Ø is the particle diameter and λ is the incident light wavelength), the charge oscillations act as a single dipole whose amplitude is strongly dependent on the distances between the surface charges, whereas the external electromagnetic (EM) field in the close vicinity of the nanoparticle surface appears static. Under these conditions, Mie scattering agrees with the more familiar Rayleigh scattering. The condition of LSPR is related to the particle polarizability, α0, expressed by Equation (2) [11]:
α = 4 π R 3 ε ( ω ) − ε d ε ( ω ) + 2 ε d
Concerning plasmonic effects, polarizability is a crucial factor, since it describes the predisposition of the electronic cloud to have its charge displaced as a result of the interaction with an electrical field, so that it is related to the dipole moment p by the relation:
p = ε0εdαE0
From Equation (4), it is possible to observe that the polarizability α is dependent on the dielectric function of the metal ε(ω) expressed by Equation (3), where ε1(ω) is the real part of the dielectric function and ε2(ω) is the imaginary part. In addition, Equation (4) shows that the polarizability is dependent on the dielectric constant of the surrounding medium, which is related to the refractive index n of the medium by Equation (2). The condition for which the polarizability α achieves the resonant enhancement, namely its maximum value, is fulfilled at the minimum values of the denominator in Equation (2) (Frölich condition). For Equation (4), the Frölich condition at which LSPR occurs is satisfied for ε1(ω) = −2εd. On this basis, to determine an LSPR in a nanoparticle, the values of ε1(ω) (the real part of the dielectric function) should be large and negative, whereas the imaginary part ε2(ω) is supposed to be negligible and positive [12]. In the case of noble metals, the dielectric function ε’m is strongly dependent on the EM field wavelength, so the bright colors displayed by metal nanoparticles definitely rely on the exact wavelength fulfilling the condition of resonance. The most used metal for LSPR sensing satisfies the resonance condition in the UV-visible region of the spectra. The bandwidth and peak position of LSPR are determined by the size, morphology, and distance of separation between the nanostructures so that they can be easily tailored and tuned in the UV-visible and NIR region of the spectrum. However, LSPR strongly depends also on the dielectric constant of the medium around the metal nanoparticles, so that, according to the changes in refractive index (RI) of the medium within the evanescent field, the particle polarizability is modified, resulting in displacements of the LSPR peak. On this basis, the sensitivity toward the changes in refractive index is exploited to detect biorecognition events occurring on particle surface, thus offering a great potential to develop sensing platforms. In Figure 2, the LSPR of a plasmonic metal nanoparticle (Figure 2A) and the SPPs (Figure 2B) are depicted.
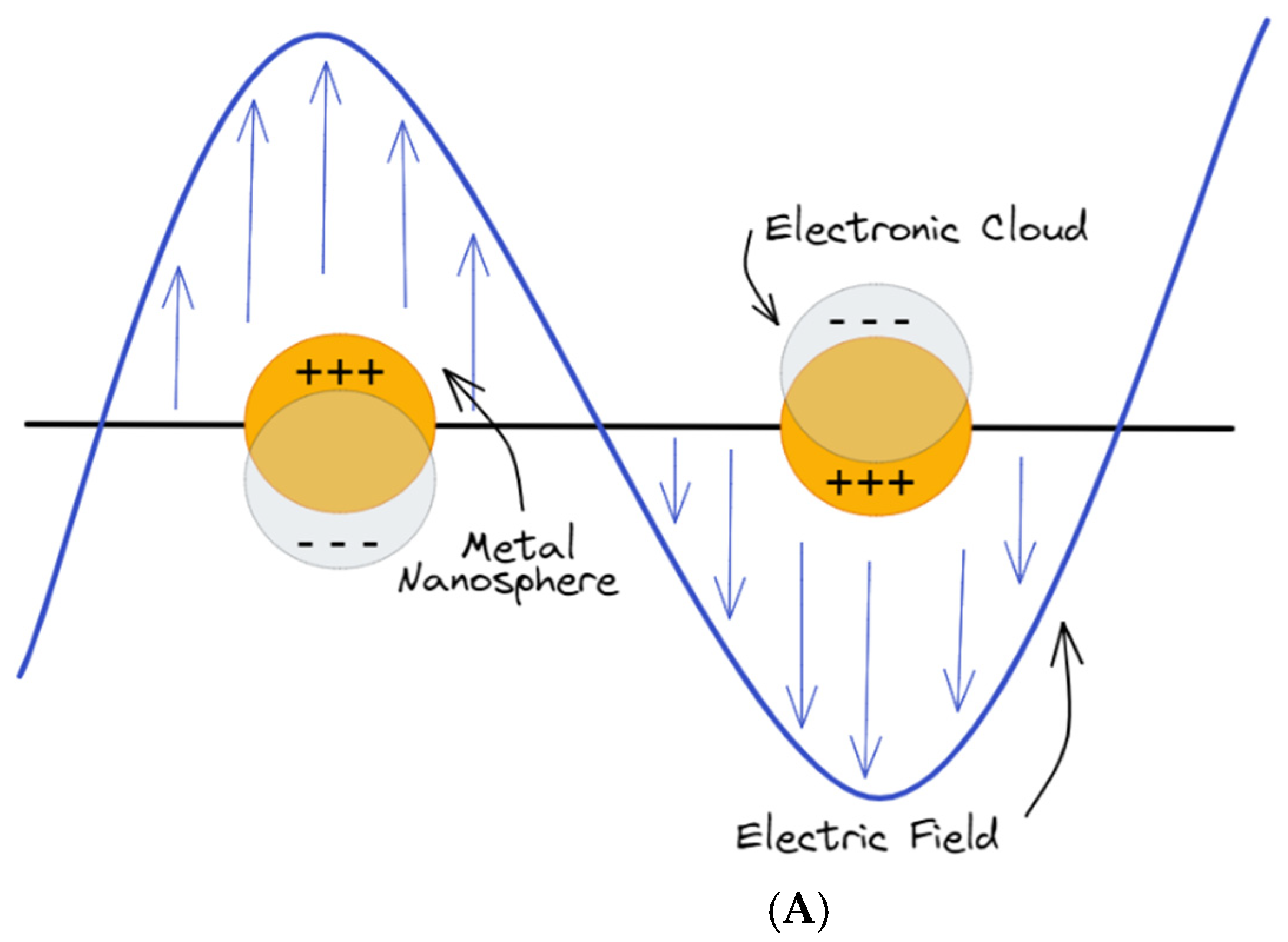
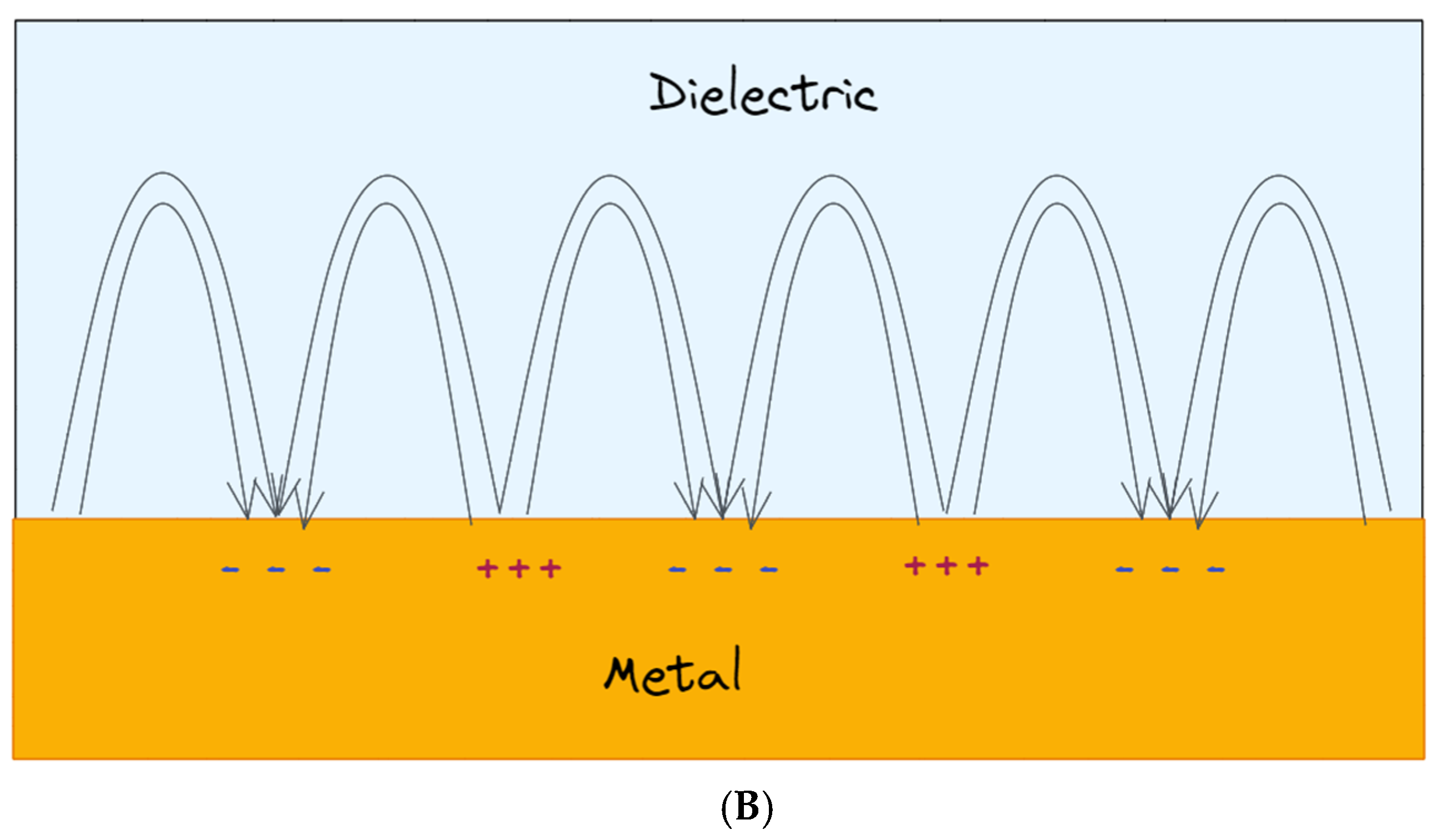
Figure 2. (A) Schematics of metal nanoparticles with their LSPR when placed in a static electromagnetic (EM) field; (B) collective charge oscillations (SPPs) at the interface between the dielectric medium and the metal.
In addition, intense and highly confined electromagnetic fields generated by the LSPRs, and localized within the gaps between metallic nanostructures, are of great interest for other sensing techniques, such as SERS. In SERS analysis, the inelastic scattering generated by molecules is greatly boosted when molecules are located closed (or adsorbed) to a rough metal surface or metal nanoparticles, thus enhancing the signal. The history of SERS is relatively short, considering that it has been observed for the first time in the work of Fleischmann in 1974 [13] in the course of Raman measurements of pyridine adsorbed on an electrochemically roughened silver surface. In 1977, two groups, observing independently that the enhanced signal did not account for the concentration of scattering species, proposed two different mechanisms: the group of Albrecht and Creighton [14] proposed a charge-transfer effect, while D. L. Jeanmaire and Richard P. Van Duyne [15] proposed an electromagnetic effect. Since then, an exponentially growing interest has been focused on improving the SERS substrates to enhance the performance of the technique but also to implement these structures in the point-of-care (PoC) devices. In the last few years, hybrid compounds composed of bidimensional nanomaterial have been exploited with an increasing frequency as SERS substrate [16], but also, other types of composites have been exploited, such as for example metal–organic framework (MOF)–gold nanoparticle (AuNPs) complexes [17].

This entry is adapted from the peer-reviewed paper 10.3390/chemosensors10070237

References

  1. Estevez, M.C.; Otte, M.A.; Sepulveda, B.; Lechuga, L.M. Trends and challenges of refractometric nanoplasmonic biosensors: A review. Anal. Chim. Acta 2014, 806, 55–73.
  2. Chen, Y.; Ming, H. Review of surface plasmon resonance and localized surface plasmon resonance sensor. Photonic Sens. 2012, 2, 37–49.
  3. Sambles, J.R.; Bradbery, G.W.; Yang, F.Z. Optical-excitation of surface-plasmons—An introduction. Contemp. Phys. 1991, 32, 173–183.
  4. Moznuzzaman, M.; Islam, M.R.; Hossain, M.B. Mehedi IM Modeling of highly improved spr sensor for formalin detection. Resul. Phys. 2020, 16, 102874.
  5. Soler, M.; Lechuga, L.M. Principles, technologies, and applications of plasmonic biosensors. J. Appl. Phys. 2021, 129, 111102.
  6. Barnes, W.L.; Dereux, A.; Ebbesen, T.W. Surface plasmon subwavelength optics. Nature 2003, 424, 824–830.
  7. Mosier-Boss, P.A. Review of SERS Substrates for Chemical Sensing. Nanomaterials 2017, 7, 142.
  8. Nie, W.; Wang, Q.; Yang, X.; Zhang, H.; Li, Z.; Gao, L.; Zheng, Y.; Liu, X.; Wang, K. High sensitivity surface plasmon resonance biosensor for detection of microRNA based on gold nanoparticles-decorated molybdenum sulfide. Anal. Chim. Acta 2017, 993, 55–62.
  9. Wriedt, T. Mie theory: A review. In the Mie Theory; Hergert, W., Wriedt, T., Eds.; Springer: Berlin, Germany, 2012; pp. 53–71.
  10. Mie, G. Beiträge zur Optik trüber Medien, speziell kol-loidaler Metallösungen. Ann. Phys. 1908, 25, 377–445.
  11. Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007.
  12. Farooq, S.; de Araujo, R.E. Engineering a Localized Surface Plasmon Resonance Platform for Molecular Biosensing. Open J. Appl. Sci. 2018, 8, 126–139.
  13. Fleischmann, M.; Hendra, P.J.; Mc Quillan, A.J. Raman spectra of pyridine adsorbed at a silver electrode. Chem. Phys. Lett. 1974, 26, 163–166.
  14. Albrecht, M.G.; Creighton, J.A. Anomalously intense Raman spectra of pyridine at a silver electrode. J. Am. Chem. Soc. 1977, 99, 5215–5217.
  15. Jeanmaire, D.L.; van Duyne, R.P. Surface raman spectroelectrochemistry: Part I. Heterocyclic, aromatic, and aliphatic amines adsorbed on the anodized silver electrode. J. Electroanal. Chem. Interfacial Electrochem. 1977, 84, 1–20.
  16. Serafinelli, C.; Fantoni, A.; Alegria, E.C.B.A.; Vieira, M. Plasmonic Metal Nanoparticles Hybridized with 2D Nanomaterials for SERS Detection: A Review. Biosensors 2022, 12, 225.
  17. Das, A.; Choi, N.; Moon, J.; Choo, J. Determination of total iron-binding capacity of transferrin using metal organic framework-based surface-enhanced Raman scattering spectroscopy. J. Raman Spectrosc. 2021, 52, 506–515.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
Video Production Service
Feedback