1. Introduction

Short-term load forecasting (STLF) is used to manage the production and distribution of electricity, and operate electricity markets from the current hour to the following days. If the electricity operator overestimates future electricity load, there will be extra production costs that will lead to economic losses. On the other hand, if the electricity demand is underestimated, power plants may not have sufficient reserves for their generators to meet the energy demanded by the grid, compromising its stability and risking the possibility of a blackout. In addition, an accurate demand forecast indirectly facilitates the management of electrical energy from renewable energies. In addition to electricity operators, other entities benefit from accurate electricity load forecasts, such as power marketers, independent system operators, or load aggregators.

Forecasting electricity load is a complex problem, which has been approached through various methods and from different points of view over the last few decades, which has led to a great variety of forecasting algorithms implemented in different electricity networks.

Many techniques are based on neural networks ^{[1] [2] [3] [4] [5]}. Other algorithms use statistical methods ^{[6] [7]}. Hybrid systems that combine neural networks with other techniques are also common ^{[8] [9] [10] [11]}.

1.1. Main Problem

STLF systems calculate forecasts frequently most likely hourly. The system must obtain fast forecasts, so the operator can read the results and manage the actions that adjust to future load. The latest measurement systems tend to use quarter-hour intervals. The STLF systems that currently work with hourly intervals will considerably increase their computational burden, whenever they change to quarter-hour intervals. They will have to forecast four times more values due to increased granularity and they will do this four times more often, due to an increase in frequency. This paper addresses the problem of computational burden while attempting to increase the accuracy of the STLF systems already implemented.

The Spanish transmission system operator (TSO) is Red Eléctrica de España (REE) and it is working on hourly intervals. It needs forecasts for 19 electrical regions, which is 19 times more calculations than a single STLF, with a total of 2.5 s for every hour that is predicted nationwide. Due to time limits for submitting predictions, it is not always feasible to calculate all future hours. Therefore, there is a schedule that determines which future intervals are predicted during each hour of the day.

The REE forecasting system cannot keep the previous forecasting schedule with quarter-hour intervals, since it is too computationally heavy to work within the time restriction. Therefore, there is need for a new schedule to forecast only the most useful intervals. Furthermore, the new schedule must be based on a criterion that numerically determines which predictions are most useful. Satisfying the need for a systematic method to optimize schedules is the main motivation of this work.

1.2. Solution Approach

It was assumed that as we approach the forecast moment, the forecast becomes more accurate. However, this hypothesis does not always hold true. There is an obvious trend in which accuracy increases as more recent information (weather and load) becomes available. Nevertheless, sometimes, there seem to be some periods in which new forecasts are actually less accurate. If accuracy loss periods can be known in advance, then the unproductive forecasts made at these times can be spared, saving computational effort while achieving a more accurate forecast. This work aims to determine the optimal schedule of forecasts so that the system only computes new forecasts when an accuracy improvement is expected.

The forecast needs to be computed within a time limit; therefore, each computer has a limit of N hourly values, beyond which the forecast would arrive late. This limit depends on the time allowed and the calculation speed, which again depends on the computer itself and on the forecasting algorithm used. In order to select the best N forecasts that can be calculated at each moment, a method to prioritize them needs to be developed. In addition, even if all predictions can be calculated, they may be counterproductive, since some of them have a greater predictive error than some of the previous ones.

2. Literature Review

The STLF field is extensive, since innumerable works have been published for decades; consequently, reviews of the state of the art have been published, such as those made by Mamum et al. ^[12], Hippert et al. ^[13], or Hong et al. ^[14].

The previous work on the STLF system used in this paper ^[15] compared the autoregressive and neural models used. The research defined which one performs better in different contexts, being determined by the model configuration, availability of data and the use of exogenous variables. On the other hand, the proposed research took into account the performance of the same model for different time lapses.

Other researchers ^{[16] [17] [18] [19] [20] [21] [22]} built and compared different STLF mathematical models employing error measures as performance indicators. After that, they did not consider how to apply those models in an optimized schedule, to avoid producing larger errors than past predictions that had already been calculated. J. Mohammed et al. ^[23] did something similar, which also included reliability indicators to assess the model’s performance.

Another example is the work carried out by G. Veljanovski et al. ^[24], in which they proposed a forecasting system based on a neural network. They did not consider the best time at which to obtain data and execute the computation.

Weyermüller et al. ^[25] built a minimalistic adaptive neuro-fuzzy inference model. It forecasts the load of one hour 24 h before, so this research could be applied to organize the calculation schedule if more forecast hours are added to the model.

The present work could complement automatic forecasting systems, since it offers an automated extra step at the end of the modeling process, in order to obtain an optimized execution schedule. An example of automatically modeled systems is the work conducted by L. Shufen et al. ^[26], in which they proposed an algorithm to automate time series forecasting for nonexperts.

The analysis proposed in this work could be applied to future works of theoretical research. For example, the research by T. Panapongpakorn et al. ^[27] or the work by D. Shuai ^[28].

Jiang et al. ^[29] examined their model for different anticipation times; they also compared different STLF models, taking into account error and computation times. However, anticipation times varied just from 5 min to 16 h ahead and they were used to assess models, in the same way that calculation times were employed to compare entire models.

There is research which focuses on reducing computational burden, such as that by A. McIlvenna et al. ^[30]. This research aims to optimize the use of a previously built forecasting system regardless of which one it is.

With a different approach, M. Weimar et al. ^[31] evaluated the improvement of a STLF system according to the economic savings with an econometric model. This is an example of how improving accuracy offers benefits that overcome developing costs.

3. Forecasting System Employed

The STLF system used in this research, during testing, is that developed by the UMH ^[8], which was implemented in REE. The system has been operating for more than 4 years, and during this time REE and UMH have continued to collaborate in continuous improvement efforts ^{[15] [32]}.

4. Methodology

The time a computer needs to calculate a set of predictions depends on three factors: the time that it takes to load new input data (I), the number of forecasts (n), and the time that it takes to make each prediction (P). So, the run time (t) can be modeled with the linear Equation (1).

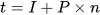(1)

Variables I and P depend on the computer and code employed. At the beginning of each hour, the forecasting system loads new input data (temperatures and previous measured load).

As mentioned before, due to the limitation of accuracy or computational burden, for each execution, there is a maximum number, N, of predictions that can be performed without exceeding the response time limit. Therefore, for each execution period, up to N predictions with greater value can be selected.

The result obtained by applying the proposed algorithm is a schedule, which defines the predictions to be executed at each hour of the day. The algorithm does not depend on the mathematical model used, but on the errors that it makes regarding historical records. Therefore, the major benefit of applying the algorithm is the error reduction sparing us from calculations with worse errors than previous ones already executed. In this way, it can be applied to a system that is organized by time intervals and it is possible to choose which intervals to predict in each hour of the day.

The Figure 1 shows how to use the algorithm in a forecasting system. First, the maximum number of predictions that can be calculated per interval is obtained, which depends on available time and computing power. At the same time, the previous year can be predicted to calculate historical error records. Finally, the algorithm is applied to obtain a schedule that will serve to forecast load during the next year.

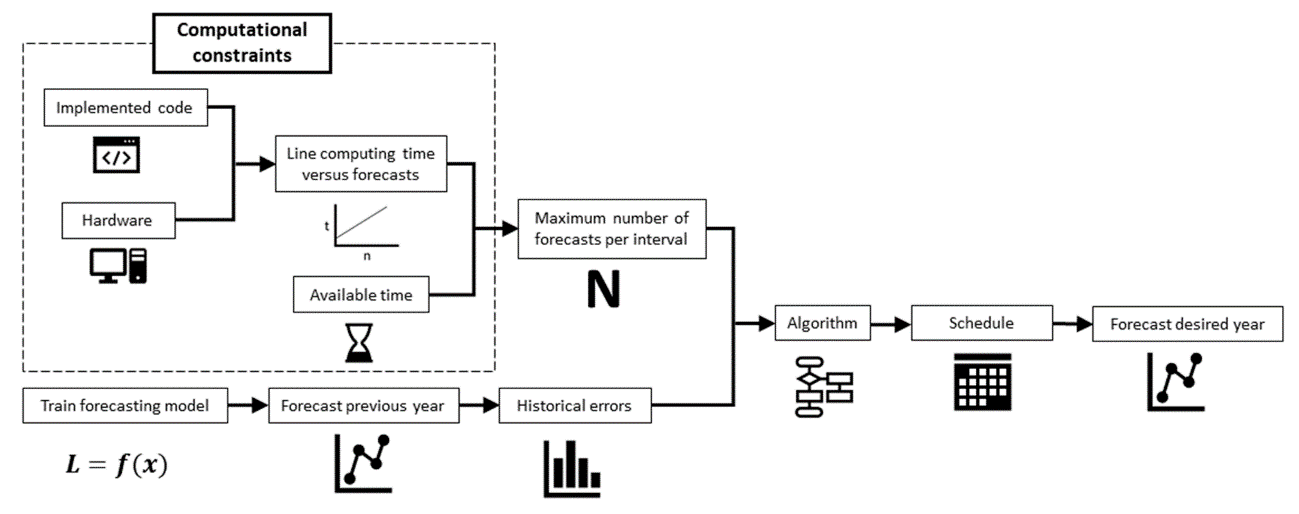Figure 1. Process summary.

Other scheduling alternatives have been tested to compare the performance of the proposed algorithm. They are explained in Table 1.

Table 1. Scheduling options.

5. Proposed Algorithm

To measure the value of a prediction, a numerical indicator called accuracy improvement expectation (AIE) is used. As the name suggests, it reflects the expectation of improvement in accuracy of a predicted demand if it is recalculated. To calculate this parameter, historical records of predictions calculated under the same conditions are used; that is, forecasts calculated at the same time of day with the same advance period.

The implemented algorithm prioritizes the hourly forecasts according to larger AIE over the results of a full year, so only the first N values will be predicted in order to adhere to the time allowed.

Before executing the algorithm, it is necessary to determine the number of maximum forecasts, N, that the computer employed can execute. This is determined empirically by its computational speed and the calculation time limit.

6. Accuracy Results of Optimized Scheduling

In order to test the proposed algorithm, the year 2019 has been predicted. The accuracy average has been calculated for all the advances of all the hours of the year. Random selection performs worse for almost all cases; it is also inconsistent, so it is ruled out as a candidate. On the contrary, the proposed algorithm offers significantly better precision than the rest of the methods.

The year 2019 has been predicted with every method. In most advances, the optimized algorithm performs better than other methods. As a final result, the year 2019 has been predicted with the current REE schedule, the algorithm, and by calculating all future hours. Except for the ninth day in advance, the algorithm always offers better accuracy. The Optimized Algorithm has a global improvement compared to the current schedule.

7. Computational burden

Last-day selection and optimized algorithm manage to compute predictions under 7 min and the first one requires less time. However, the optimized algorithm offers better accuracy in most cases.

The Spanish electricity system operator requires future load of 19 electrical regions. Nowadays, the entire forecasting horizon spans up to 240 h, thus the total of future loads that can be predicted extends to 4560, which require 10.16 min. However, if the quarter-hour system is employed, the number of future intervals to forecast will multiply by four. This new system will entail 18,240 numbers to be calculated in 40.62 min, which is unfeasible since REE requires results before 7 min have passed.

According to Equation (1) and quarter-hour intervals, the maximum number of forecasts to compute in 7 min is 3140. So, there is time to forecast 165 intervals in every electrical region. Therefore 165 is the maximum value that can be used on the algorithm as number N of forecasts.

8. Conclusions

This research has developed an algorithm that organizes the calculation schedule of a STLF system throughout the day. The schedule obtained is adapted to the computational capacity of the computer while actually increasing the system accuracy. The methodology can be applied to any forecasting technique, even if computational burden is not an issue because it has been proven that limiting the number of forecasts can be beneficial for accuracy, as it has been demonstrated for the case of REE.

On the other hand, according to results, the main contribution of the work is to reduce the computational load of a predictive system without sacrificing accuracy. This will allow a transition to the quarter-hour system with an optimal execution schedule.

This paper offers a first approach to improving forecasting systems through calculation planning. Applying a similar study to other time series prediction systems could improve them in a similar way. As future work, it is proposed to use the algorithm to plan the new quarter-hour system of the Spanish TSO.

This entry is adapted from the peer-reviewed paper 10.3390/en15103670